无线电能传输装置空心线圈间的互感计算

徐百汇，高 嵬



无线电能传输装置空心线圈间的互感计算

徐百汇1，高 嵬2

（1.海军东海舰队装备部，浙江宁波315122；2. 海军工程大学电气工程学院, 武汉430033）

无线电能传输系统中，线圈间的分隔距离以及不对中，使得系统的最大效率得不到保证。本文基于一个更加有效和普适的模型，重新推导了用于评估圆形线圈间互感的数学模型，并适用于存在及不存在不对中情况的两种条件。同时，文中给出了利用MATLAB软件得出的计算结果。这些结果为后期无线电能传输系统中线圈的设计、计算积累了理论和计算基础。关键词：无线电能传输 线圈 互感

0 引言

无线电能传输系统能够实现电能经由线圈，以高频电磁场作为媒介传输到电气设备[1–3]，但由于线圈本身的距离和不对中等因素影响，往往无法实现电能传输效率的最大化。

基于线圈是否对中的条件计算线圈间的互感是研究线圈互感问题的基本途径[1–6]。基于麦克斯韦定律、诺依曼定律、毕-萨定律以及磁矢量方法等的应用，文献[3-7]给出了很多种互感计算模型。这些模型以解析或半解析的形式，通过椭圆积分的第一、二或第三种形式给出，即霍伊曼-蓝布达方程、贝塞尔方程和拉格朗日方程[6-10]。尽管如此，一个更加先进和相关度更高的模型已经在[6,7]文献中推导得出，该模型对评估不对中线圈的互感大有帮助。

本文的目的在于，在是否考虑同轴位置的情况下，利用对于文献[6,7]中进行修改后更加有效和普适的模型，重新梳理推导出用于评估两线圈间互感的数学模型。同时，并非像文献[7,10]中仅仅给出计算结果，本文中的结果通过MATLAB以图形化的形式给出。最后，计算结果与文献[7,10]中的结果进行比较，相关错误进行了纠正，结果进行了修正。

1 互感计算模型

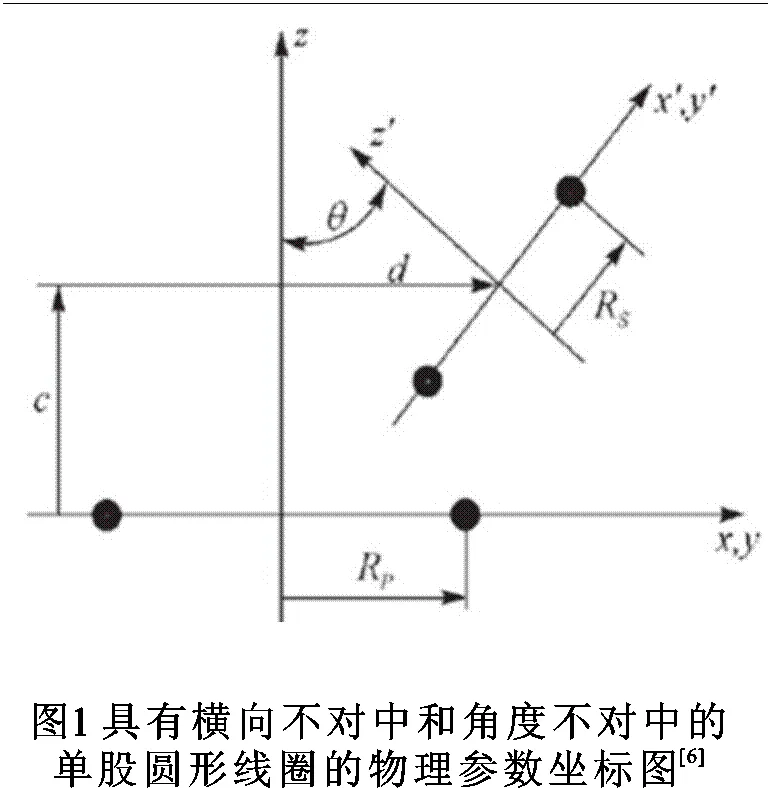
在文献[6]中，该文作者推导出一种更加有效和普适的模型，用以计算两个不同轴的单股圆形线圈间的互感（参见式（1）和图（1））。而式（1）中给出的模型是基于诺依曼积分方法的应用得出的。为了证实该模型的正确性，文献[10]的作者利用磁矢量方法得出了另外一个互感模型（参见文献[10]之式（20））。然而，文献[7]的作者使用与文献[10]的作者所采用的同样方法，通过详细的推导过程，还原了文献[6]作者的推导结论[7]。

(1)

，

，

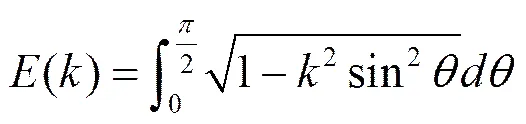
其中µ0为真空磁导率，R和R分别为初级、次级线圈的半径，为横向位移，为线圈物理几何学的形状系数，为线圈中心间的分隔距离，为线圈间的角位移，k为一变量，参数()为其函数，为次级线圈任意点的集成角，,和为无量纲参数，()和()分别为第一类和第二类全椭圆积分。

2 用于互感计算的数学模型的再推导

在式（1）中，初级和次级线圈的匝数并未给出，这一点非常重要。因此，需要基于文献[7]中给出的例子考虑匝数，从而给出重新推导的如下的模型。

2.1情形1：没有不对中

图2给出了无不对中的情况（即θ=0以及d=0），因此，单股圆形空心线圈的互感数学模型可表示为：

应该说，这种表达式只是（1）式的一个特殊情况，从图2的复杂程度也可明显得出结论。一般来说，我们更倾向于采用这一种线圈布置方式。

2.2情形2：只有横向不对中

图3给出了只有横向不对中的情况（即θ = 0），此时单股圆形空心线圈的互感数学模型可表示为：

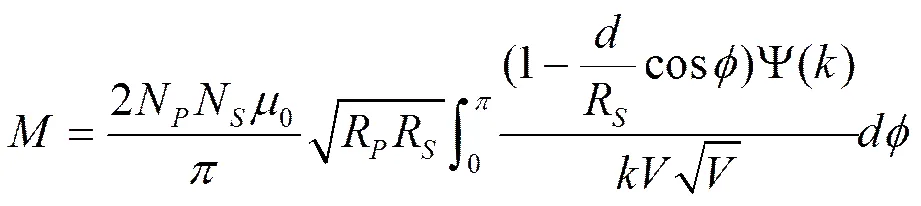
2.3情形3：只有角度不对中

图4给出了只有角度不对中的情况（即= 0），此时单股圆形空心线圈的互感数学模型可表示为：

其他参数的定义与（1）相同。

2.4情形4：横向和角度均不对中

图1给出了两种位移同时存在的情况，即考虑初级和次级绕组匝数，此时单股圆形空心线圈的互感数学模型可表示为：

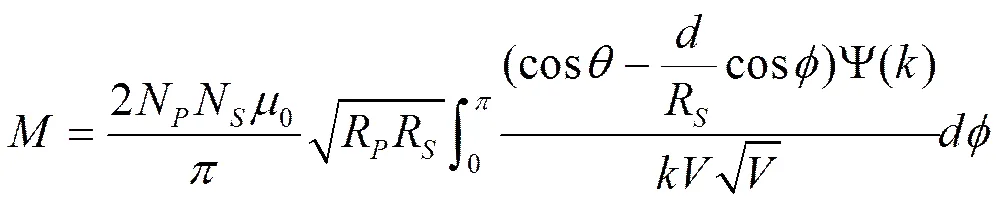
其参数的定义均与（1）相同。

3计算模型结果分析

圆形空心线圈互感的计算结果如图5-图9所示，其边界条件为考虑及不考虑横向不对中和角度不对中。利用MATLAB软件重新推导的模型如式（2）-式（5）所示，另外，所有的图形结果为图2-图5，而数据结果可参见表1。图5中展示的结果为文献[7,10]中的数据计算结果（见表1），其主要原因在于这两篇文献中的例子只考虑了横向不对中，即虽然线圈间的分隔位移（即=0,0.05 m和0.1 m）在文中均有考虑，但此两篇文献作者重点只关注=0的情况，其他情况并未进行讨论。

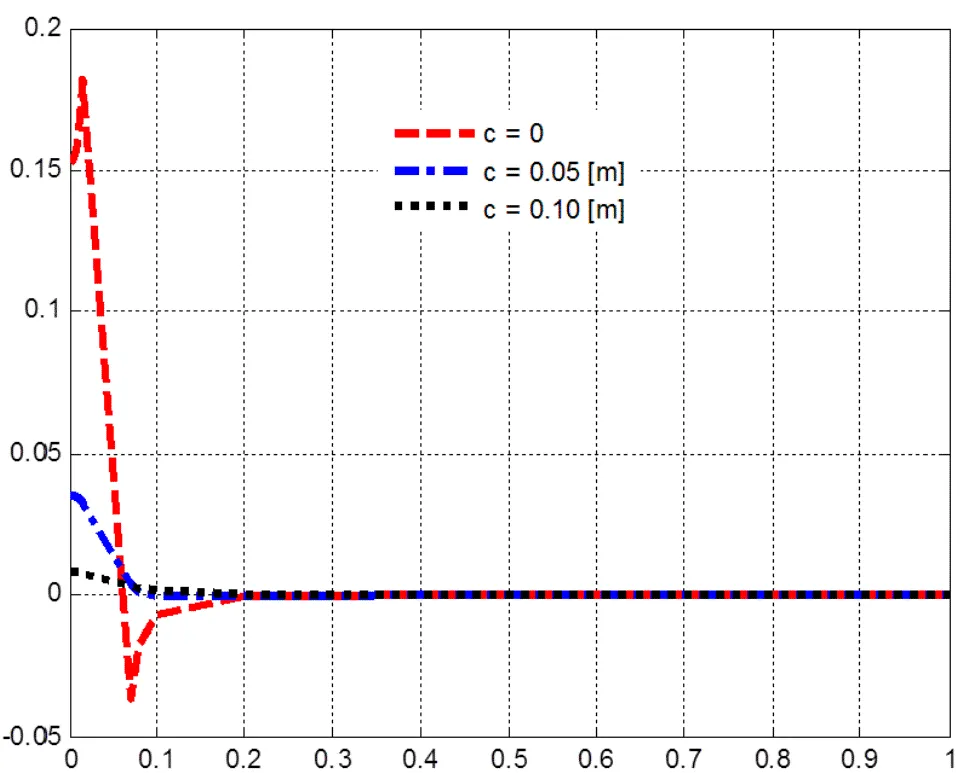
图5 横向不对中时互感与横向不对中量的关系

文献[7]的结果表明，从=0到=15.5 mm（即次级线圈在初级线圈之内）的范围内，互感从0.15 mH增长到018 mH。这一结果与该文中的结论一致（参见图5和表1）。但是，与文献[10]的结果相比却有很多不同。此外，从=69.5 mm到1000 mm（即次级线圈在初级线圈之外），文献[7]的结果表明，对于更大的值（从=200 mm到1000 mm），互感会出现负值，但最终趋于零。这一结果与本文的图5和表1的结果非常吻合。而且这一结论是符合电磁学理论的，原因在于次级线圈交链的磁力线在初级线圈的外侧改变了方向[6-8]。但在文献[10]中，当位于外侧的次级线圈的尺寸比初级线圈的尺寸小很多时，互感趋近于零的速度变慢，同时不会出现负值，这一点与理论不符。因此，文献[7]的结论是正确的，而文献[10]中的式（20）结论是错误的。

这一研究表明，随着线圈分隔距离和位移的增大，线圈互感是减小的（见图5-图9）。因此，应该通过增大初级线圈内交流电流的频率来实现互感值的增大，同时线圈的相关部分应使用电容和铁氧体磁芯进行补偿。

4 结论

本文对考虑及不考虑不对中条件时两线圈间互感的数学模型进行了重新推导，同时利用MATLAB进行了仿真，将所得结果与之前相关文献结果进行比对，验证和澄清了相关结论，为下一步开展线圈互感的设计、计算进行了有益的探索和积累。

图6 角度不对中时互感与线圈分隔距离的关系

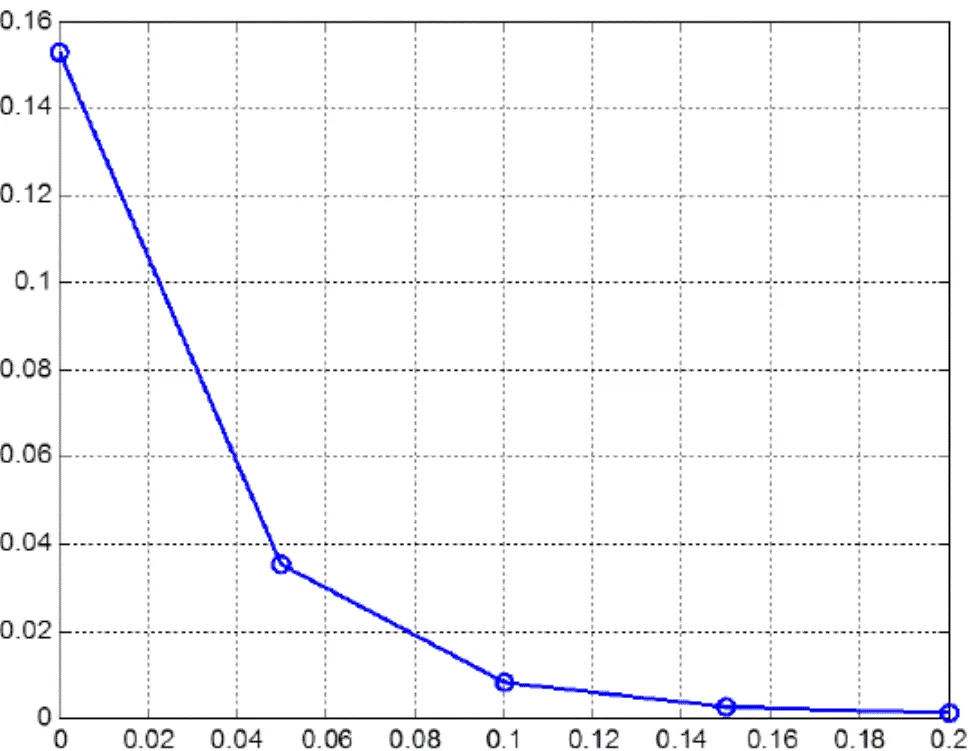
图7 无不对中时互感与线圈分隔距离关系

图8 不对中时互感与横向不对中量的关系（c=0）

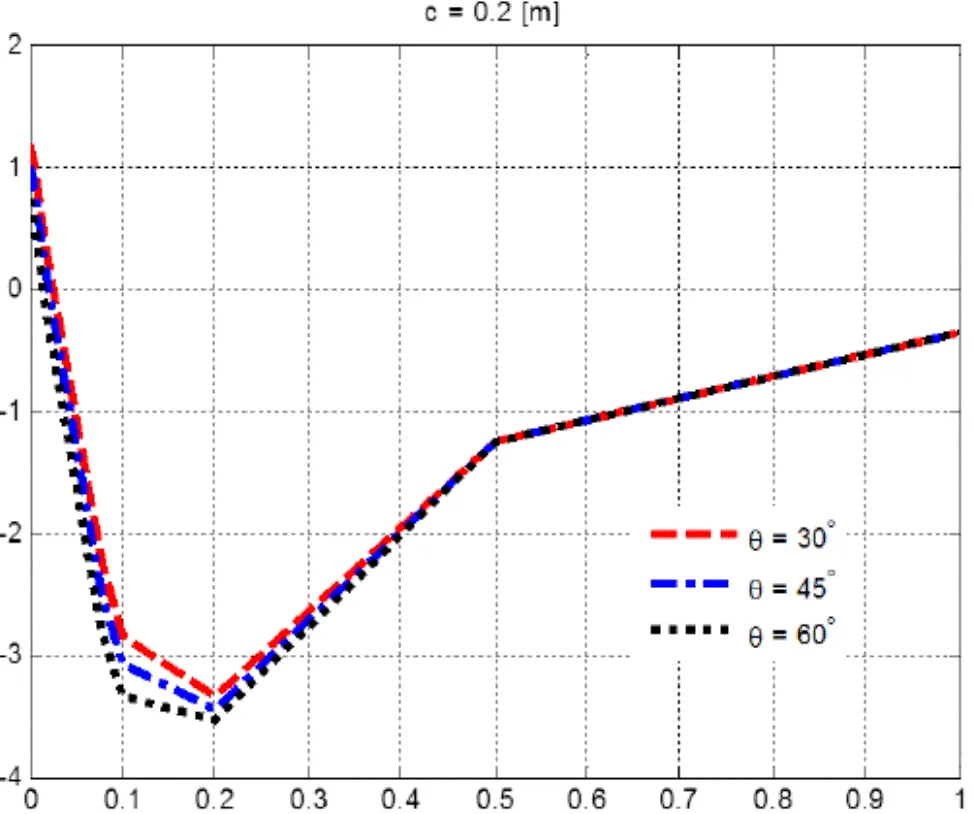
图9 不对中时互感与横向不对中量的关系（c=0.2）

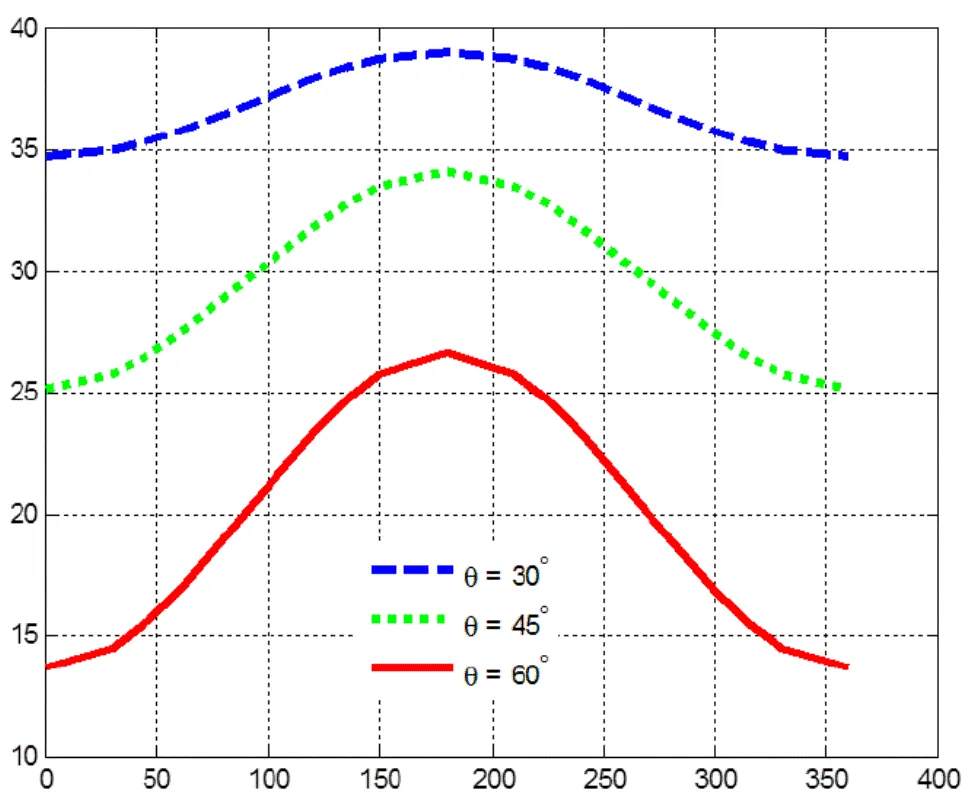
图10 不对中时互感与角度不对中量的关系

[1] 全汝岱，解光勇，王霖. 基于电磁耦合机构的非接触电能传输系统[J].大学物理实验, 2009，22(4)：1-3.

[2] 田子建．具有中继谐振线圈的磁耦合谐振无线电能传输系统[J]. 电工技术学报，2015，30(12)：168-174.

[3] 肖思宇．耦合谐振式无线电能传输系统的线圈优化[J]. 电工技术学报，2015, 30（1）：221-225.

[4] 翟渊，孙跃，戴欣等. 磁共振模式无线电能传输系统建模与分析[J]．中国电机工程学报, 2012,32(12):155-160.

[5] JC Maxwell. A treatise on electricity and magnetism[M]. 1954.

[6] FW Grover 1944.Inductance calculations, working formulas and tables[C]. Proceedings of the I.R.E.,1944: 620-629．

[7] SI Babic, F Sirois and C Akyel. Transformer leakage flux models for electromagnetic transients: Critical review and validation of a new model[C]. 2009 ,(8):15-26.

[8] 傅文珍，张波，丘东元等. 自谐振线圈耦合式电能无线传输的最大效率分析与设计[J].中国电机工程学报, 2009, 29(18):21-26.

[9] AO Anele, Y Hamam, Y Alayli etc.. Computation of the mutual inductance between air-cored coils of wireless power transformer[J]. Journal of Physics: Conference Series, 2015,633:(1).

[10]M Liao, E Levi, Z Zabar and L Birenbaum. Analysis of generator-driven linear induction launchers[J]. IEEE Trans. Mag.,1997,33(1):184-189.

Calculation of Mutual Inductance of Air-cored Coils in a Wireless Power Transfer System

Xu Baihui1, Gao Wei2

(1.Armament Department of East China Sea Fleet of PLA Navy, Ningbo 315122, Zhejiang, China; 2.Electrical Engineering School of NUE, Wuhan 430033, China)

In the wireless power transfer system, the coil separation distance and misalignment, maximum power transfer is not guaranteed. Based on a more efficient and general model available in the literature, rederived mathematical models for evaluating the mutual inductance between circular coils with and without lateral and angular misalignment are presented. Rather than presenting results numerically, the computed results are graphically implemented using MATLAB codes. The results are presented to establish a basement for designing and calculating the mutual inductance in WPT system.

wireless power transfer (WPT); coil; mutual inductance

TN806

A

1003-4862（2017）01-0035-05

2016-11-15

徐百汇（1965-），男，硕士，高级工程师。研究方向：舰船装备管理。Email:depkin@163.com