秦皇岛河流-海岸水动力和水质耦合模拟分析

顾 杰, 胡成飞, 李正尧, 匡翠萍, 张永丰



秦皇岛河流-海岸水动力和水质耦合模拟分析

顾 杰1, 胡成飞2, 李正尧3, 匡翠萍3, 张永丰4

(1. 上海海洋大学海洋科学学院, 上海 201306; 2. 浙江省水利河口研究所, 浙江杭州 310020; 3. 同济大学土木工程学院水利工程系, 上海200092; 4. 河北省海洋环境监测中心, 河北秦皇岛 066002)

基于MIKE FLOOD建立秦皇岛入海河流及其近岸海域一维、二维耦合河流-海岸水动力和水质模型, 研究了秦皇岛海域和入海河流的水动力和污染物分布规律。结果表明: (1)海域潮流为半日潮, 其中石河口南北支入海口流速变化过程差别较大, 但水位变化过程基本一致; (2)整体上河流入海口化学需氧量(COD)与流速呈正相关关系; (3)COD在近岸海域的扩散方向与涨落潮潮流方向一致, 各入海河口海域落潮流期间的COD高于涨潮流。如上结论为赤潮爆发机理和应急处置研究提供科学依据和技术支持。

秦皇岛; 一二维耦合模型; 水动力; 化学需氧量(COD)

秦皇岛市是我国著名的滨海旅游胜地, 以丰富的海产养殖资源和独特的区位优势逐渐成为京津冀地区经济的重要部分[1]。然而近年来秦皇岛近岸海域承受的环境压力不断加大, 入海污染物总量持续增加, 生态环境趋劣, 海洋赤潮等生态灾害频发[2-3]。2009年秦皇岛沿岸海域爆发大面积赤潮, 2010年秦皇岛昌黎沿海海域发生大面积赤潮[4-6]。持续不断地赤潮灾害对秦皇岛海域生态平衡、水产资源等构成了长期潜在的危害, 同时给滨海旅游业的发展带来了极大威胁[7]。因此, 有效地控制污染物排海总量, 是减少赤潮暴发、抑制海洋环境污染、推动经济发展与环境保护协调统一、保证海洋生态环境可持续发展的关键技术环节。

国内外学者对各种水域的水环境已做过大量研究。在水动力方面, 陈景秋等[8]建立了重庆两江汇流水动力模型, 模拟分析了汇流比及滨江路建设对流场的影响。陈祖军等[9]建立了长江口水域三维非线性斜压浅海与陆架模型能较好地反映了长江口水域的三维水动力状况。李䶮等[10]开发了潮汐河网水动力模型, 模拟了珠江三角洲市桥河上雁洲水闸建闸前后不同调度方案对市桥河水动力过程的影响。张越美和孙英兰等[11]建立了渤海湾三维变动边界潮流模型, 分析了潮流场的时空分布特点。魏泽勋等[12]建立了海洋环流诊断模型来研究渤海夏季环流。Fossati等[13]建立了三维水动力模型计算近岸海域复杂的环流模式。De Marchis等[14]建立了三维水动力模型用以模拟Augusta湾的水动力现状。在水质方面, 杨家宽等[15]利用WASP6水质模型对汉江襄樊段水质进行模拟研究。Li等[16]采用模糊算法建立了二维模糊水质模型, 并用其计算突发性污染事件。Tang等[17]基于MIKE 11建立了一维水动力和污染物扩散模型, 用以计算南水北调工程的水质风险。Bedri等[18]建立了三维水动力和水质模型, 用来研究电厂关闭后对都柏林湾浴场水质的影响。Zhao等[19]建立了三维水动力和水质模型, 来模拟异龙湖水动力、污染物扩散和富营养化状态。国家海洋局北海预报中心[20]开发了三维溢油漂移预测模型以模拟水下溢油三维运动, 掌握溢油油污的轨迹及浓度分布等信息。

将一维模型与二维或三维模型耦合嵌套, 发挥各自优势, 来解决河流-海岸和河流-湖泊等地区水动力或污染物扩散问题是必要和有意义的[21]。现如今, 多维模型的耦合计算应用越来越广泛, 大量学者对其进行了研究。徐祖信和尹海龙[22]构建了平原感潮河网地区一维、二维水动力耦合模型。卢吉和余锡平[23]建立了河流海岸综合水动力学模型, 将其应用于研究长江口及口内感潮河道内径流与潮流的相互作用。王佳等[24]运用一、二维耦合模型, 对开凿胶莱运河改善渤海水质的效果进行了初步研究。Zhou等[25]耦合了珠江三角洲河网的一维水动力、水质模型和珠江三角洲河口的三维水动力、水质模型。Lai等[26]在耦合了一维非恒定流模型和二维水动力模型的基础上建立了耦合水动力分析模型(CHAM), 研究了长江流域的水动力状况。Chen等[27]基于MIKE FLOOD耦合了一维(MIKE 11)和二维(MIKE 21)水动力及扩散模型来模拟河流和沼泽的水文水质状况。本文基于秦皇岛近岸海域的研究, 建立秦皇岛河流-海岸一二维耦合水动力和污染物扩散数学模型, 将入海河流-河口-近岸海域三者作为一个系统整体研究河口海岸地区水动力和污染物扩散规律, 分析污染物从河流到海域的分布规律。

1 研究区域与方法

1.1 区域概述

秦皇岛市位于河北省东北部, 东与辽宁省接壤, 西与唐山市相邻, 北邻承德, 南濒渤海。地处中纬度地带, 属暖温带湿润半湿润大陆季风性气候, 受我国东部沿海季风环流的影响, 气候四季分明, 气温年差较大, 年降水量多寡变化显著。秦皇岛市夏暖冬寒的气候特征十分明显, 年平均日照时间2 700~ 2 850 h; 年平均气温10.5~11.3℃[28]。秦皇岛年平均降水量650~750 mm, 降水集中在7~9三个月, 占全年的70%~80%, 年平均蒸发量1 468.7 mm。

1.2 数学模型建立

MIKE软件包是由河口海岸与海洋模拟软件、城市水模拟软件和水资源综合管理模拟软件构成。软件包数学模型的科学性与合理性已得到世界公认, 在丹麦、希腊、印度及中国香港等国家和地区都得到了成功的应用。本文利用MIKE FLOOD将秦皇岛入海河流一维(MIKE 11)水动力和水质模型与秦皇岛近岸海域二维(MIKE 21)水动力和水质模型进行耦合, 发挥各自的计算优势, 研究分析秦皇岛“入海河流-河口-近岸海域”的水动力和污染物扩散分布规律。

1.2.1 一维模型

MIKE 11模型主要应用于河口、河流、灌溉系统和其他内陆水域的水文学、水力学、水质和泥沙输运模拟。

1.2.1.1 水动力模型

应用有限差分法求解一维Saint-Venant方程组来模拟河流水位和流量随时间和一维空间的变化, 方程如下:

(2)

式中:表示河流断面径流量;表示沿水流方向的距离;表示时间;表示过水断面面积;表示旁侧入流量; g表示重力加速度;表示水深;表示曼宁系数;为过水断面的水力半径;为动量校正系数[29]。

1.2.1.2 水质模型

一维水质模型的输运过程主要表现为纵向扩散作用。污染物质的转化过程主要由污染物质自身特性决定, 包括化学和生化反应等过程[30]。对流扩散(AD)模块使用隐式有限差分格式对一维对流扩散方程进行求解, 一维对流扩散方程如下:

(3)

式中:表示物质浓度;表示扩散系数;表示污染物线性衰减系数;2表示污染物源/汇浓度。

1.2.2 二维模型

MIKE 21模型主要应用于河流、湖泊、河口、海湾、海岸和海洋等水域的水流、波浪、泥沙及环境。

1.2.2.1 水动力模型

在笛卡尔坐标系下, 在Navier-Stokes方程的基础上通过对三维动量方程和连续方程沿深度进行积分, 得到二维浅水方程, 如下:

连续方程:

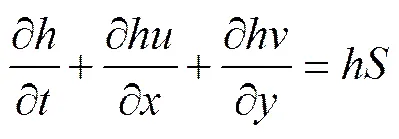
动量方程:

(6)

式中:是源汇项流量;表示水位;=+,为总水深;为静止水深;与表示和方向上的沿水深平均流速;为柯氏力系数(为地球自转角速率,为地理纬度);为水体密度;sx和sy表示和方向上的风应力;bx和by表示和方向上的底部摩擦力; 侧应力包括黏性摩擦和紊动摩擦等。通过对涡黏方程沿水深平均流速梯度方向计算如下(式中表示水平涡黏系数):

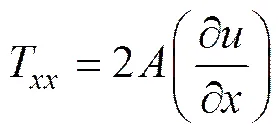
1.2.2.2 水质模型

MIKE 21水质模型是在对流扩散计算的基础上, 加载ECOLab模块中的状态变量变化过程。水质模型基本控制方程如下:

式中p表示污染物的衰减率, 在本研究中, 化学需氧量(COD)的衰减变化方程与MIKE 11水质模型中一致;C为水平扩散项:

(9)

式中h为水平扩散系数。

1.2.3 一二维耦合模型

MIKE FLOOD是一个把一维模型和二维模型进行动态耦合的建模系统。利用这种耦合方式, 计算模型能够拓展模拟的水环境规模, 发挥各模块优势的同时, 形成互补。在本研究中, 通过MIKE FLOOD的标准链接, 将MIKE 11一维河网模型与MIKE 21近岸海域二维模型进行耦合, 进而完整模拟秦皇岛河流-海岸水动力和污染物扩散过程。

在MIKE FLOOD标准链接中, MIKE 11和MIKE 21采用显式连接进行水动力耦合计算。MIKE 11需要MIKE 21第+1步的计算水深作为其从步到+1步的水位边界条件, 因此MIKE 21水动力计算总是领先MIKE 11一步。水动力耦合计算过程中, MIKE 11和MIKE 21的链接断面被映射到MIKE 21中一个或多个单元, 其即作为MIKE 21计算的边界条件。当MIKE 21第+1步计算完成后, 返回其一个或多个单元的平均水位作为MIKE 11第+1步计算的水位边界条件。如此反复, 完成一、二维水动力耦合计算。

在污染物扩散模型计算中, 连接处污染物的浓度计算取决于MIKE 11和MIKE 21(式中分别简写M11、M21)间的水流方向。当水流从MIKE 11流向MIKE 21时, 污染物作为MIKE 21的源输入:

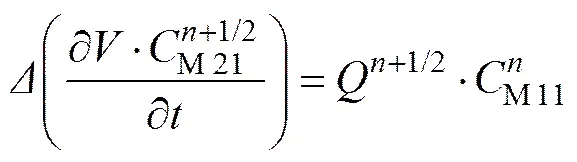
当水流从MIKE 21流向MIKE 11时, MIKE 21中扩散方程修正为:

(11)

1.2.4 模型范围和计算网格

秦皇岛近岸海域数学模型研究范围北起石河口以北约20 km处, 南至滦河口以南约17 km处, 陆域岸线约197 km, 外海延伸至离岸约50 km的海域。模型包含秦皇岛9大主要入海河口和10条入海河流(汤河和小汤河均由汤河口入海), 沿岸线从北向南河口依次为: 石河口、汤河口、新河口、戴河口、洋河口、人造河口、东沙河口、大蒲河口和滦河口。各条河流的研究范围为其潮流界上游至入海河口。计算网格为无结构三角形网格(如图1所示), 网格节点共计2 942个, 三角形单元共计5 418个。网格分辨率按研究需求进行控制, 河口海岸地区网格较密, 分辨率可达15 m, 外海网格较为稀疏, 边界处分辨率约为6 600 m。

1.2.5 边界条件、初始条件和参数设置

1.2.5.1 边界条件、初始条件

秦皇岛河流-海岸一二维耦合水动力和水质数学模型共有10个入海河流上游开边界和3个外海开边界。入海河流上游开边界由河流实测流量和COD过程控制。水质模型COD初始0取各河流6月实测平均值, 为56~84 mg/L。3个外海开边界水动力设定采用流速和水位条件控制其潮位和流速过程由渤海潮流模型(边界为大连到烟台)[3]提供。污染物设定由本底污染物浓度控制, 模型初始COD设为本底值1.3 mg/L, 外海SW和SE边界COD取1.2 mg/L, NE边界COD取1.3 mg/L。

1.2.5.2 相关参数设置

计算时间步长变化范围为0.001~2 s。河道内, 曼宁系数由河流底床泥沙粒径和水深综合确定, 取0.02~0.05 s/m1/3; 扩散系数、COD在20℃时的降解系数20和COD的Arrhenius温度系数COD通过水质模型率定, 分别取10~100 m2/s, 0.05~0.4 d–1和1.02。近岸海域内, 曼宁系数由该海域海床泥沙中值粒径和水深综合确定, 取平均值74 m1/3/s。h通过污染物扩散模型率定, 取常值120 m2/s。20为0.001~0.038 4 d–1,COD通过模型率定取1.02。

1.3 模型验证

选择有实测资料的时段(即赤潮高发期夏季)分别进行水动力及水质验证。实测水文资料包括2013年5月大小潮潮位、流速和流向, COD采用由河北省海洋环境监测中心提供的8月秦皇岛近岸海域水质站点实测数据。水动力及水质测站站点位置如图2、图3所示。数学模型的计算时间为2013年5月1日至8月31日, 选择与实测资料相同时间段的计算值与对应的实测值比较来验证数学模型。

1.3.1 水动力模型验证

1.3.1.1 潮位验证

水动力数学模型大小潮潮位验证如图4所示, 验证点位置如图2所示。潮位计算值在相位和趋势上与实测值基本吻合, 潮位大小略有偏差, 主要是由于秦皇岛潮位站位置靠近海岸线, 近岸海域地形复杂, 且站点处于无潮点影响范围内, 潮波变形较大等原因。

1.3.1.2 潮流验证

水动力数学模型大小潮流速流向验证如图5、图6所示, 典型站点SDL08验证点位置如图2所示。模型在大小潮期间的涨落潮流速和流向过程的计算值在相位和数值上与实测值均较为吻合, 计算流速和流向在数值上与实测值存在一定误差, 这主要是由于水动力模型中部分物理参数采用了平均值, 且秦皇岛近岸海域位于渤海无潮点附近, 潮波变化复杂。总体上, 水动力数学模型较好地模拟了秦皇岛近岸海域水动力变化特征。

1.3.2 污染物输移模型验证

入海河流污染输入是近岸海域的主要污染源, 因此需对秦皇岛河流-海岸一二维耦合数学模型中的近岸海域污染物扩散模型进行验证。COD验证如图7所示, COD计算结果相对误差小于20%的站点占总数的100%, 相对误差小于10%的站点达到站点总数的67.9%, 模型总体验证良好, 能较好地模拟了秦皇岛近岸海域污染物扩散分布特征。

本文采用百分比偏差(PBIAS, 式中用指代)对秦皇岛河流-海岸一二维耦合数学模型进行评价。

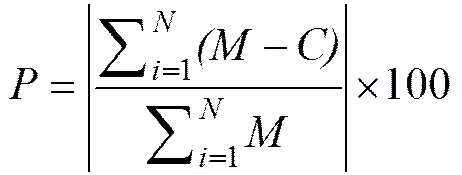
式中是实测值;是计算值;是实测值个数。当<10时, 模型效率评价为极好; 当10≤<20时, 模型效率评价为很好; 当 20≤<40时, 模型效率评价为好; 当≥40时, 模型效率评价为差[31]。计算可得=2.30~38.57, 评价为极好~好。整体上, 秦皇岛河流-海岸一二维耦合数学模型验证良好, 可反映秦皇岛河流-海岸水动力和污染物扩散分布特征。

图7 近岸海域COD验证

Fig. 7 Verification of chemical oxygen demand (COD) in coastal waters

2 模拟结果分析

河流-海岸地区的水动力和污染物输运规律在河流上游以河流特性为主, 口外海滨以海洋特性为主, 河口段则受河流和海洋特性强弱交替的相互作用, 有其独特的性质。选取2013年8月18~19日大潮期间分析秦皇岛河流-海岸地区污染物扩散分布特征。

2.1 入海河流污染物分布规律

石河口三角洲将石河入海口分为南北两支入海, 具有独特的动力和污染物扩散分布特性, 选取石河为代表河流, 研究秦皇岛入海河流的污染物分布规律。石河入海口N1(北支, 距分流点600 m)和S1(南支, 距分流点500 m)点处的水位、流速和COD分别如图8和图9所示, 其中流向从上游指向下游为正。从水位、流速过程曲线可以看出, 石河北支入海口在2013年8月18日02: 00~12: 00为涨潮落潮流, 12: 00~17: 00为涨潮涨潮流, 17: 00~18: 00为落潮涨潮流, 00: 00~ 02: 00和18: 00~23: 00为落潮落潮流; 南支入海口在2013年8月18日02: 00~07: 00和11: 00~ 17: 00为涨潮落潮流, 07: 00~11: 00为涨潮涨潮流, 00: 00~02: 00和17: 00~23: 00为落潮落潮流, 无落潮涨潮流阶段。南北支入海口水位变化过程基本一致, 而流速变化过程差别较大, 这主要受石河径流量在南北支入海口的分流比、南北支入海口纳潮量及其断面地形等因素影响。南、北支入海口流速在8月18日均经历了2次增减变化, 并且海域的潮流判别系数小于0.5, 为半日潮。无论在南支还是北支, 在8月18日大潮期间涨潮涨潮流和落潮涨潮流的历时之和均小于涨潮落潮流和落潮落潮流的历时之和, 南支入海口甚至无落潮涨潮流阶段, 说明石河口为弱潮性河口, 径流占主导作用。

从COD过程曲线可以看出, 整体上南北支入海口COD变化过程随流速变化而变化, 流向指向入海口时, 南北支入海口COD与流速大小呈正相关关系, 流速增大, COD增大, 流速减小, 单位时间里河流COD入海通量相对减小, 导致COD减小; 流向从入海口指向上游时, 南北支入海口COD受海水的影响较大, 均呈下降趋势。

2013年8月18日高低潮位时刻, 石河COD分布如图10所示, 其中轴坐标零点为河口口门, 指向河流上游为正。在潮流界下游, COD受海水影响显著下降, 且潮流界在高潮位时距入海口较低潮位时刻更远。高潮位时刻, 从石河入海口分流点到近岸海域, 南支COD呈下降趋势, 北支COD则呈先下降后上升趋势。低潮位时刻, 从分流点到近岸海域, 南北支入海口COD均呈下降趋势, 且北支COD高于南支COD。

秦皇岛近岸海域COD分布如图11所示, 涨落潮典型时刻的选取与上节一致。秦皇岛近岸海域潮流总体特征为顺岸往复流。总体上, 各入海河口海域落潮流期间COD高于涨潮流, COD在近岸海域的扩散方向与涨落潮潮流方向一致。河口海域COD受径流和潮流的共同作用, 在涨急至落急期间, 近岸海域COD逐渐增大, 这是由于秦皇岛近岸海域潮流较弱, 多数入海河流在涨急至涨憩期间, 河流指向近岸海域, 且随着涨潮流流速的减小, 河流入海流速逐渐增大, 从而导致近岸海域COD亦逐渐增大。同理在落急至涨急期间, 随着落潮流流速的减小和涨潮流增强, 河流入海流速亦逐渐减小, 从而导致近岸海域COD略有降低。

石河口与洋河口海域转流时间不同步, 石河口附近海域在相位上领先洋河口附近海域。在洋河口海域落憩时刻, 石河口海域已为涨潮阶段, 海域COD相对较小。对于石河口海域, 除涨急时刻外, 其余典型时刻, 北支入海口海域COD均高于南支入海口海域浓度。

3 结论

1) 海域潮流为半日潮, 整个海域转流时间略微有差异。其中石河有南、北二个分支入海, 受南、北支分流比、南北支入海口纳潮量及其断面地形等因素的影响, 南、北支的入海口流速变化过程差别较大, 但水位变化过程基本一致, 由海域潮汐决定。

2) 整体上河流入海口化学需氧量(COD)与流速呈正相关关系。高潮位时刻, 从石河入海口分流点到近岸海域, 南支COD呈下降趋势, 而北支COD则呈先下降后上升趋势。低潮位时刻, 从分流点到近岸海域, 南、北支入海口COD均呈下降趋势, 且北支COD高于南支。

3) COD在近岸海域的扩散方向与涨落潮流流向一致。各入海河口海域落潮流期间COD高于涨潮流期间。涨急至落急期间, 近岸海域COD逐渐增大, 而落急至涨急期间则略有降低。

[1] 兰冬东, 李冕, 许妍, 等. 渤海水质监测站位优化研究[J]. 海洋科学, 2016, 40(4): 88-93. Lan Dongdong, Li Mian, Xu Yan, et al. Layout optimization of water quality monitoring stations in the Bohai Sea[J]. Marine Sciences, 2016, 40(4): 88-93.

[2] Liu Shuguang, Lou Sha, Kuang Cuiping, et al. Water quality assessment by pollution-index method in the coastal waters of Hebei Province in western Bohai Sea, China[J]. Marine Pollution Bulletin, 2011, 62(10): 2220-2229.

[3] Wang Liping, Liu Lusan, Zheng Binghui. Eutrophication development and its key regulating factors in a water-supply reservoir in North China[J]. Journal of Environmental Sciences-China, 2013, 25(5): 962-970.

[4] 匡翠萍, 胡成飞, 冒小丹, 等. 秦皇岛海域洪季水动力及污染物扩散数值模拟[J]. 同济大学学报(自然科学版), 2015, 43 (9): 1355-1360. Kuang Cuiping, Hu Chengfei, Mao Xiaodan, et al. Numerical simulation of hydrodynamics and pollutant transport in Qinhuangdao coastal water in the flood season[J]. Journal of Tongji University(Natural Science), 2015, 43(9): 1355-1360.

[5] 古彬, 甄毓, 米铁柱. 秦皇岛扇贝养殖区褐潮暴发期浮游微藻群落结构特点研究[J]. 中国海洋大学学报(自然科学版), 2015, 45(7): 64-72. Gu Bin, Zhen Yu, Mi Tiezhu.Characterization of phytoplankton community in the coastal waters of Qinhuangdao during brown tide[J]. Periodical of Ocean University of China, 2015, 45(7): 64-72.

[6] Zhang Qingchun, Qiu Limei, Yu Rencheng, et al. Emergence of brown tides caused by Aureococcus anophagefferens Hargraves et Sieburth in China[J]. Harmful Algae, 2012, 19: 117-124.

[7] 吴彤, 陈艳拢, 黄凤荣, 等. 基于统计学方法的秦皇岛海域营养盐长时序变化分析[J]. 海洋环境科学, 2015, 34(4): 499-502. Wu Tong, Chen Yanlong, Huang Fengrong, et al. Variation trends of nutrient in Qinhuangdao coastal area based on statistical method[J]. Marine Environmental Science, 2015, 34(4): 499-502.

[8] 陈景秋, 赵万星, 季振刚. 重庆两江汇流水动力模型[J]. 水动力学研究与进展(A辑), 2005(S1): 829-835. Chen Jingqiu, Zhao Wanxing, Ji Zhengang. The hydrodynamic numerical model of the confluence of Yangtze River and Jialing River in Chongqing[J]. Journal of Hydrodynamics, 2005(S1): 829-835.

[9] 陈祖军, 韦鹤平, 陈美发. 长江口水域三维水动力数值模拟研究[J]. 海洋预报, 2004, 21(3): 37-44. Chen Zujun, Wei Heping, Chen Meifa.Numerical simulation of three-dimensional hydrodynamics in the Changjiang Estuary [J]. Marine Forecasts, 2004, 21(3): 37-44.

[10] 李䶮, 曾凡棠, 关洪林, 等. 水闸联合调度下河网水动力过程数值模拟研究[J]. 人民长江, 2013, 44(23): 35-37. Li Yan, Zeng Fantang, Guan Honglin, et al. Hydrodynamic process simulation of river network influenced by coordinative dispatch of sluices[J]. Yangtze River, 2013, 44(23): 35-37.

[11] 张越美, 孙英兰. 渤海湾三维变动边界潮流数值模拟[J].青岛海洋大学学报(自然科学版), 2002, 32(3): 337-344. Zhang Yuemei, Sun Yinglan. A three-dimensional numerical tidal model with a variable boundary for the Bohai Bay [J]. Journal of Ocean University of Qingdao, 2002, 32(3): 337-344.

[12] 魏泽勋, 李春雁, 方国洪, 等. 渤海夏季环流和渤海海峡水体输运的数值诊断研究[J]. 海洋科学进展, 2003, 21(4): 454-464. Wei Zexun, Li Chunyan, Fang Guohong, et al. Numerical diagnostic study of the summertime circulation in the Bohai Sea and the water transport in the Bohai strait [J]. Advances in Marine Science, 2003, 21(4): 454-464.

[13] Fossati M, Piedra-Cueva I. A 3D hydrodynamic numerical model of the Río de la Plata and Montevideo’s coastal zone[J]. Applied Mathematical Modelling, 2013, 37(3): 1310-1332.

[14] De Marchis M, Freni G, Napoli E. Three-dimensional numerical simulations on wind- and tide-induced currents: The case of Augusta Harbour (Italy)[J]. Computers & Geosciences, 2014, 72: 65-75.

[15] 杨家宽, 肖波, 刘年丰, 等. WASP6水质模型应用于汉江襄樊段水质模拟研究[J]. 水资源保护, 2005, 21(4): 8-10. Yang Jiakuan, Xiao Bo, Liu Nianfeng, et al. Simulation on the water quality for Xiangfan Reach of Hanjiang River using WASP6[J]. Water Resources Protection, 2005, 21(4): 8-10.

[16] Li Ruzhong, Shigeki Masunaga, Hong Tianqiu, et al. Fuzzy model for two-dimensional river water quality simulation under sudden pollutants discharged[J]. Journal of Hydrodynamics, 2007, 19(4): 434-441.

[17] Tang Caihong, Yi Yujun, Yang Zhifeng, et al. Water pollution risk simulation and prediction in the main canal of the South-to-North Water Transfer Project[J]. Journal of Hydrology, 2014, 519, Part B: 2111-2120.

[18] Bedri Z, Bruen M, Dowley A, et al. Environmental consequences of a power plant shut-down: A three- dimensional water quality model of Dublin Bay[J]. Marine Pollution Bulletin, 2013, 71(1-2): 117-128.

[19] Zhao Lei, Li Yuzhao, Zou Rui, et al. A three-dimensional water quality modeling approach for exploring the eutrophication responses to load reduction scenarios in Lake Yilong (China)[J]. Environmental Pollution, 2013, 177: 13-21.

[20] 黄娟, 曹丛华, 赵鹏, 等. 渤海溢油三维漂移数值模拟研究[J]. 海洋科学, 2015, 39(2): 110-117. Huang Juan, Cao Conghua, Zhao Peng, et al. Development and application of a three-dimensional oil spill model for the Bohai Sea [J]. Marine Sciences, 2015, 39(2): 110-117.

[21] 张修忠, 王光谦. 河道及河口一维及二维嵌套泥沙数学模型[J]. 水利学报. 2001(10): 82-87. Zhang Xiuzhong, Wang Guangqian. 1-D and 2-D nesting sediment transport model for rivers and estuaries [J]. Journal of Hydraulic Engineering, 2001(10): 82-87.

[22] 徐祖信, 尹海龙. 平原感潮河网地区一维、二维水动力耦合模型研究[J]. 水动力学研究与进展, 2004, 19(6): 744-752. Xu Zuxin, Yin Hailong. Development of coupled one-dimensional and two-dimensional hydrodynamic model for tidal rivers[J]. Journal of Hydrodynamics, 2004, 19(6): 744-752.

[23] 卢吉, 余锡平. 河流海岸水动力学综合模型[J]. 清华大学学报(自然科学版), 2009, 49(6): 820-824. Lu Ji, Yu Xiping. River and coastal hydrodynamics integrated model[J]. Journal of Tsinghua University (Science and Technology), 2009, 49(6): 820-824.

[24] 王佳, 江毓武, 万振文. 一、二维耦合模式在“胶莱运河”中的应用[J]. 海洋与湖沼, 2009, 40(2): 145-151. Wang Jia, Jiang Yuwu, Wan Zhenwen. Numerical simulation on the Jiaolai Canal with a 1-D and 2-D coupling model[J]. Oceanologia Et Limnologia Sinica, 2009, 40(2): 145-151.

[25] Zhou Nianqing, Westrich Bernhard, Jiang Simin, et al. A coupling simulation based on a hydrodynamics and water quality model of the Pearl River Delta, China[J]. Journal of Hydrology, 2011, 396(3-4): 267-276.

[26] Lai Xijun, Jiang Jiahu, Liang Qiuhua, et al. Large-scale hydrodynamic modeling of the middle Yangtze River Basin with complex river–lake interactions[J]. Journal of Hydrology, 2013, 492: 228-243.

[27] Chen Chunfang, Meselhe Ehab, Waldon Michael. Assessment of mineral concentration impacts from pumped stormwater on an Everglades Wetland, Florida, USA - Using a spatially-explicit model[J]. Journal of Hydrology, 2012, 452-453: 25-39.

[28] 同济大学, 河北省发改委宏观经济研究所, 北海监测中心, 等. 北戴河邻近海域污染物总量控制与产业结构优化调整[R]. 上海: 同济大学, 2016. Tongji University, Hebei Development and Reform Commission Macroeconomic Research Institute, Beihai Monitoring Center, et al. Control of total amount of pollutants and optimization of industrial structure in Beidaihe[R]. Shanghai: Tongji University, 2016.

[29] DHI. MIKE21 & MIKE3 FLOW MODEL hydrodynamic and transport module scientific documentation[Z]. Demark: DHI Water & Environment, 2011.

[30] 魏泽彪. 南水北调东线小运河段突发水污染事故模拟预测与应急调控研究[D]. 济南: 山东大学, 2014. Wei Zebiao. Simulation and emergency disposal research on sudden water pollution of Xiaoyun River for the eastern route of the South-to-North Water Diversion Project[D]. Ji’nan: Shandong Umiversity, 2014.

[31] Allen J I, Somerfield P J, Gilbert F J. Quantifying uncertainty in high-resolution coupled hydrodynamic- ecosystem models[J]. Journal of Marine Systems, 2007, 64(1-4): 3-14.

Coupling simulation and analysis of hydrodynamics and water quality in Qinhuangdao rivers and coastal waters

GU Jie1, HU Cheng-fei2, LI Zheng-yao3, KUANG Cui-ping3, ZHANG Yong-feng4

(1. College of Marine Sciences, Shanghai Ocean University, Shanghai 201306, China; 2. Zhejiang Institute of Hydraulics and Estuary, Hangzhou 310020, China; 3. Department of Hydraulic Engineering, College of Civil Engineering, Tongji University, Shanghai 200092, China; 4. Marine Environment Monitoring Center of Hebei, Qinhuangdao 066002, China)

By coupling a one-dimensional model of river with a two-dimensional model for coastal waters in Qinhuangdao, a model of hydrodynamics and water quality was established based on the MIKE FLOOD. The characteristics of flow currents and distribution of pollutants in Qinhuangdao estuaries and coastal waters were subsequently analyzed. Numerical results show that 1) the tidal current in coastal water is semidiurnal, and although there is considerable change in the current speeds of the north and south branches of the Shihe River estuary, the water level is basically the same. 2) There is a positive correlation between chemical oxygen demand (COD) concentrations and current speeds in Qinhuangdao estuaries. 3)The direction of COD transport in coastal waters corresponds to the direction of the tidal current, and the COD concentration is higher in the ebb period than that in the flood period. The above results provide a scientific basis and technical support for research into the red-tide outbreak mechanism and emergency treatment thereof.

Qinhuangdao; one- and two-dimensional coupled model; hydrodynamics; chemical oxygen demand

X55

A

1000-3096(2017)02-0001-11

10.11759/hykx20160815001

2016-08-15;

2016-12-12

海洋公益性行业科研专项(201305003-5)

顾杰(1961-), 男, 江苏兴化人, 教授, 博士, 主要研究环境水力学和海岸工程等, 电话: 15692166507, E-mail: jgu@shou.edu.cn;李正尧, 通信作者, 硕士研究生, 主要研究河口、海岸及近海工程, lemon_yao@yahoo.com

Aug. 15, 2016

[Special Scientific Research of Marine Public Welfare Industry, No. 201305003-5]

(本文编辑: 刘珊珊)