球形气泡界面变化对尾涡性质和尺寸的影响
费洋,庞明军
球形气泡界面变化对尾涡性质和尺寸的影响
费洋,庞明军
(常州大学机械工程学院,江苏省绿色过程装备重点实验室,江苏常州213164)
利用计算流体力学法研究了中等Reynolds数下(25≤≤500)气泡界面污染程度对其尾流的影响。借鉴圆球绕流和停滞帽模型,提出了一种模拟中等Reynolds数下受污染球形气泡尾流的三维模型,气泡界面污染程度取决于帽角()的大小,帽角越大表示气泡表面污染程度越小。研究发现:=25~200时,污染程度的减小会减小尾涡长度()、分离角()以及涡中心位置()和()的数值,但不会改变其与Reynolds数表征的关系;污染程度的减小会使=250~500时尾涡的三维特性减弱,使=350时有序脱落的尾涡的强度减小并最终使其不发生脱落,使=500时无规律脱落的尾涡的无序性减弱并最终使其不发生脱落。
气泡;界面;尾流;层流;流体动力学
引 言
许多工业领域比如核能发电、化工、食品加工中都存在泡状流动。在这些流动中,气泡或多或少会受到污染,气泡受污染后它的界面会发生变化,界面变化会使气泡的尾流发生变化,进而使气泡的阻力系数和其他水动力学特性发生变化。因此,深入研究气泡界面变化对尾流的影响具有重要意义。为了研究气泡界面污染程度对其水动力学特性的影响,目前国内外研究者均以在液相中加入不同浓度的表面活性剂作为污染源来开展研究。表面活性剂分子作为污染源会吸附在气泡表面上。对于一个上浮气泡,表面活性剂分子在对流的影响下会从气泡上部表面不断地扩散到气泡的尾部形成聚集现象[1-6]。
目前有关气泡尾流的研究主要集中于纯净气泡,Bhaga等[7]实验研究了不同Eötvös数()、Morton数()和Reynolds数()下气泡的尾涡长度、宽度和涡中心位置随Reynolds数的变化关系;倪明玖[8]使用VOF方法研究了气泡尾部尾涡的形成机理,发现尾涡的形成主要源于气泡顶部与底部存在的压差,同时也受气泡尾部环流的影响;Tripathi等[9]模拟发现椭球形气泡沿直线上升时的尾涡是对称的,沿曲线上升时的尾涡是不对称的;Gumulya等[10]模拟研究了椭球帽形气泡和裙状气泡的尾涡长度随雷诺数的变化规律。有关受污染气泡的尾流研究,Veldhuis等[11]实验发现气泡在纯净水和自来水中上浮时的尾流结构明显不同;Saito等[12]和Huang等[13-14]实验发现因表面活性剂在气泡表面分布不均而产生的Marangoni效应会对气泡的尾流产生影响。由上述可知,目前对纯净气泡尾流的研究相对较深入,但对受污染气泡尾流的研究仅局限于气泡污染前后其尾流的变化情况,没有涉及气泡表面污染程度不同时,其尾流的变化情况。因此,有必要详细研究气泡界面污染程度对其尾涡性质、尺寸和脱落情况的影响。
针对受污染气泡的数值研究,主要有模型假设和真实模拟两种方法。模型假设是基于对气泡表面给予一定的假设进行研究的,主要有均匀模型[15]、停滞帽模型[16-21]和摩擦系数模型[22]。均匀模型假设气泡表面均匀污染,但这一假设不符合运动气泡上表面活性剂的实际分布,故目前的模拟大多基于图1所示的停滞帽模型,但停滞帽模型又难以对界面污染程度进行定量控制。摩擦系数模型用摩擦系数来表示气泡的污染,总体上与停滞帽模型类似。虽然近些年相关学者不使用任何模型假设实现了真实情况下受污染界面的模拟,但由于交界面处的输运方程需在伸缩与变形的交界面上求解,且还伴有网格的重构,故大多均停留在二维模拟阶段[23-25]。然而Fleckenstein等[3]通过对比二维和三维的模拟结果发现,两种维度下气泡的尾流情况大不相同。因此,想要更真实获得受污染气泡的尾流情况,就必须进行三维模拟。
本文使用计算流体力学法研究了中等Reynolds数下球形气泡界面污染程度对其尾涡性质、尺寸和脱落情况的影响。由于气泡在中等Reynolds数下运动时其Marangoni数通常小于1(=¥/b,是气体常数,是吸附温度,¥是气泡界面上的极限浓度,是液相的动力黏度,b是气泡的运动速度),即气泡表面两种界面条件接近于阶跃过渡[19-20],为方便研究,本文借鉴圆球绕流和停滞帽模型,提出了一种模拟中等Reynolds数下受污染球形气泡尾流的三维简化模型,通过改变帽角大小来表示气泡表面的污染程度,即帽角越大表示受污染程度越小。这一模型有效地避免了现有模型难以实现三维模拟以及单纯停滞帽模型难以定量控制界面污染程度的缺点。
1 数值计算
1.1 几何建模及边界条件
鉴于目前所研究的问题,参考文献[18-19,26]的建模方法,采用如图2所示直径为的圆球域作为计算区域,将直径为的气泡固定在圆球域中心,而流体相对气泡发生流动,即,将-左半球设置为速度进口边界条件,进口液相速度为,将-右半球设置为出流边界条件(除了静压,其他所有参数均为零)。对于圆球域与气泡的直径比/,本文综合考虑表1所示各学者[18-19,26]的取值,为同时保证模拟的准确性和节省计算时间,取/=64。坐标原点设在气泡中心上,轴正方向为流体流动方向。为便于生成六面体网格,将气泡表面和圆球域表面六等分。为考虑不同污染程度时气泡的尾流情况,参考停滞帽模型,将气泡分为图3和图4所示的迎流面和背流面两部分,并将背流面分成图4所示的21小块,然后通过改变边界条件来控制气泡的污染程度。若帽角=0°(表示气泡完全污染),将气泡表面上所有的面都设为无滑移壁面边界条件,即气泡表面存在切应力、不存在滑移速度,此时气泡就类似于一个固体颗粒;若帽角=180°(表示气泡未受污染),将气泡表面上所有的面都设为无穿透壁面边界条件,即气泡表面存在滑移速度,不存在切应力;若帽角在0°~180°之间,表示气泡部分污染,气泡表面上两种边界条件共存。为了便于建模,本文基于二分法,取部分污染气泡的帽角90°,135°,157.5°和168.75°。若帽角90°,将气泡的背流面,即图4中的面6-26设为无滑移壁面边界条件;若帽角135°,将图4中气泡背流面中的10-26设为无滑移壁面边界条件;若帽角157.5°,将图4中气泡背流面中的18-26设为无滑移壁面边界条件;若帽角168.75°,将图4中气泡背流面中的26设为无滑移壁面边界条件。
1.2 网格划分
对于网格划分,本文采用六面体网格。由于球形气泡和圆球域为轴对称结构,因此流域内的总网格单元数由圆球域投影圆周上的网格份数和沿流域半径上的网格份数决定。本文设气泡投影圆周上的网格份数、流域投影圆周上的网格份数与流域半径上的网格份数相等。由于气泡表面的网格数也会对模拟结果产生一定影响,本文通过借鉴表1所示各学者[18-19,26]在流域投影圆周上的网格份数,为同时保证模拟的准确性和节省计算时间,取流域投影圆周上的网格份数为128个,即气泡表面的网格数为6144个、流域内网格单元数约为78.64万个。有关气泡投影圆周上网格份数的无关性检验见2.1节。

表1 域的尺寸与气泡投影圆周上的网格数
此外,为了更好地捕捉气泡尾流的变化,本文进行非均匀网格划分,使靠近气泡表面的网格较为密集,远离气泡表面的网格较为稀疏。加密后气泡表面第一层网格厚度与为满足梯度要求而所需的边界层厚度有关,表2中罗列了Tomboulides等[27]给出的不同Reynolds数下所需边界层厚度的需求值re以及本文加密后气泡表面第1层网格的厚度use,可以看出实际值小于需求值,即这一比例下的第1层网格厚度满足梯度要求。球形气泡表面上的网格和流域中某一截面的网格分别如图5和图6所示。

表2 不同Reynolds数下所需边界层厚度的理论值和第1层网格厚度的实际值
1.3 控制方程与数值方法
从Kim等[28]给出的圆球绕流实验结果可以看出,当Reynolds数大于800时,尾流才会表现出湍流性质,并出现小尺度的涡结构。因此,为节省计算时间,采用较为简单的层流模型进行计算。此时,需求解的连续性方程和动量方程如式(1)和式(2)所示[29]
Ñ=0 (1)
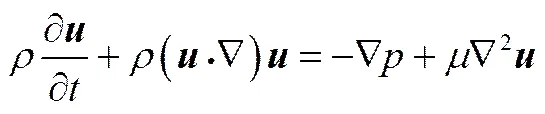
式中,是液相速度,m·s-1;是静压,Pa;是液相动力黏度,Pa·s。
下文中的阻力系数由阻力求得,阻力由黏性力和压力梯度力组成,如式(3)~式(6)所示[30]

(4)
(5)

式中,D为阻力,N;DV为黏性力,N;DP为压力梯度力,N;D为阻力系数;为气泡直径,m;b为气泡运动速度(这里等于进口液相速度),m·s-1;为液相密度,kg·m-3;为气泡表面的静压,Pa;x为气泡表面切应力的流向分量,Pa;为气泡表面积,m2;x为气泡表面法向单位矢量的流向分量。
本文使用非稳态时间格式迭代求解,求解时压力-速度耦合采用SIMPLEC算法以加快收敛速度,单元中心的变量梯度采用最小二乘法离散,对流项采用具有三阶精度的QUICK离散格式以减小伪扩散,压力项采用二阶精度离散格式,时间项采用二阶隐式离散格式。参考文献[27],时间步长的设置如表3所示。

表3 不同Reynolds数下的时间步长
对于后文中的模拟结果,长度尺度用气泡直径量纲1化,速度尺度用进口液相速度量纲1化,时间尺度用/量纲1化。
1.4 工况设置
从圆球绕流的研究结果可知,在≤500的中等Reynolds数下,存在3种临界Reynolds数:1=212[27],2=277.5[31]和3=420[32]。当≤210时,为稳态轴对称尾流[33];当=220~270时,尾流由两个平面对称的发夹涡组成[33];当=280~420时,涡开始脱落,但涡脱落的方向相同[31-32];当>420时,尾涡开始无规律脱落[32]。因此本文将依据文献划分的3种区间,分别对受污染气泡的尾流进行分析和讨论。此外,为对≤200时尾流随Reynolds数的变化规律进行深入分析,故在此区间内取多个Reynolds数进行模拟,具体工况设置如表4所示。
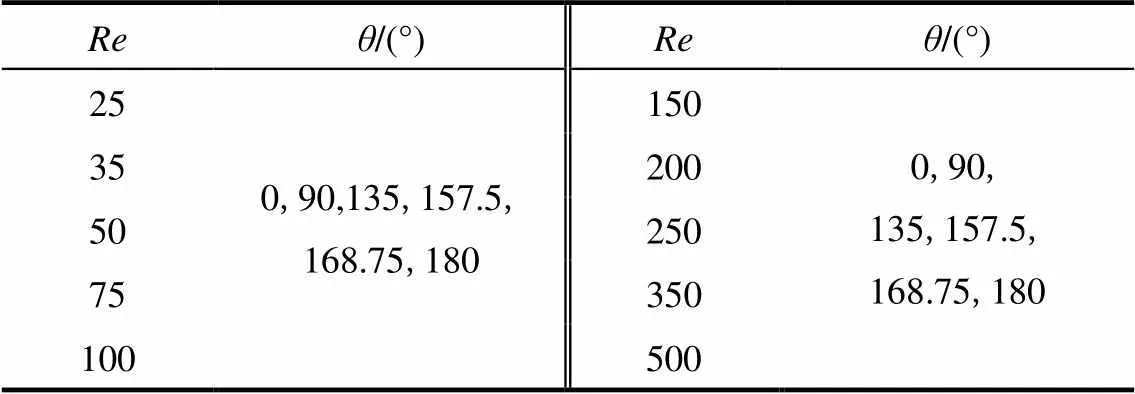
表4 工况设置
2 结果分析
2.1 网格无关性检验
气泡圆周上网格的份数会对计算的准确性造成影响,本文分别取气泡投影圆周上网格的份数为64、96、128、160和192份,并在最大Reynolds数=500下,对干净气泡和完全污染气泡的阻力系数进行监测,计算收敛时的监测结果如表5所示。可以看出,气泡圆周上网格的份数为64份时的模拟结果与其他模拟结果相比有明显偏差,本文为同时保证模拟结果的准确性和节省时间花费,取气泡圆周上网格的份数为128份。

表5 气泡圆周上不同的网格份数对干净气泡和完全污染气泡的阻力系数的影响 (Re=500)
2.2 结果准确性检验
为确认本文提出的简化模型和参数设置的准确性,下文将模拟所得完全污染气泡和干净气泡在不同下的阻力系数与Mei等[34-35]给出的公式[式(7)和式(8)]所对应的阻力系数值进行比较,如图7所示。从中可以看出,完全污染气泡的阻力系数与Mei等[34]给出的公式吻合得很好,干净气泡的阻力系数与Mei等[35]给出的公式有少量的偏差,这是由于真实情况下气泡内存在微弱的流动,流动强度随污染程度的减小而增加[36],而本简化模型忽略了气泡内部的流场,但与真实情况相比偏差相对较小。
界面完全污染球形气泡阻力系数的计算表达式[34]

界面完全干净球形气泡阻力系数的计算表达式[35]
(8)
有关结果准确性的进一步检验见下文图11。
2.3 气泡界面变化对其尾流的影响分析
2.3.1=25~200时尾涡性质随帽角的变化 由于=25~200时气泡尾流的表现形式相同,故下文仅对图8所示=150时,不同帽角下的尾流进行分析。从图中可以看出,随着帽角的增加,尾涡的面积不断减小,当帽角≥157.5°时,尾涡将完全消失。由此可见,图7中同一下干净气泡的阻力系数小于受污染气泡的阻力系数正是由尾涡面积的减小和尾涡的消失造成的。此外,Takagi等[37]认为气泡受污染后减速的原因源于阻力系数的增加,由此可以推断,尾涡面积的增大能降低气泡在静置液中的上升速度。这与通常所认为的气泡上浮减速源于交界面流动性的降低并不矛盾,因为交界面流动性的降低在本文中就是指帽角的减小,帽角的减小会使尾涡面积增大。这一点在能量守恒上是成立的,因为气泡上升速度降低后节约下来的动能被尾涡所消耗。对气泡尾涡尺寸随Reynolds数变化的具体分析见2.3.2节。
此外,从图8中还可以看出,对于有尾涡形成的帽角区间,帽角0°的完全污染气泡,其尾流的表现形式与Tomboulides等[27]模拟的刚性颗粒的尾流表现形式相同,呈二维轴对称形式;帽角=90°的半污染气泡,其尾流也呈轴对称形式;而帽角=135°的部分污染气泡,尾流的表现形式与完全污染和半污染时的不同,有微弱的三维特性产生,为平面对称形式。出现这一现象的原因与气泡表面流向静压在帽角处的跳跃有关,图9给出了帽角=0°,90°和135°下气泡表面压力系数p沿流向分布,可以看出,帽角=135°时气泡表面流向静压在帽角处有一个跳跃现象,它的存在使易受干扰的分离流线发生了变化,而帽角=0°和90°时泡表面流向静压在帽角处不存在这一跳跃现象。
2.3.2=25~200时尾涡尺寸随帽角的变化 为了定量分析气泡受污染程度对其尾流的影响,Taneda[38]定义了如图10所示用来描述尾流的相关参数(即尾涡长度、涡中心位置和以及分离角),并预测了这些参数随Reynolds数的变化情况。由于=250~500时流线呈明显的三维特性,难以对尾涡准确描述,且帽角≥157.5°时,尾涡完全消失,故本文将用这些变量对=25~200范围内、帽角≤135°时,气泡的尾涡进行深入分析,并给出其随的变化曲线。
图11是帽角=0°、90°、135°时气泡尾涡的相关尺寸:尾涡长度/、涡中心位置/和/以及分离角随Reynolds数的变化。可以看出,帽角的变化只是改变了曲线上在数值上的大小,没有对其随Reynolds数的变化趋势造成影响。
2.3.3=250~500时尾涡性质和尾涡尺寸随帽角的变化 图12为=250~500时不同帽角下的流线图,可以看出:当帽角=0°时,流线杂乱无章;当帽角帽角=90°时,流线的混乱程度有所减小,对称性有所增加;当帽角帽角=135°时,流线的三维特性已经变得很弱,接近于二维特性;当帽角≥157.5°时,流线的三维特性消失,呈轴对称形式。此时,依旧能推断出图7中同一Reynolds数下干净气泡的阻力系数小于受污染气泡的阻力系数正是由尾涡面积的减小和尾涡的消失造成的。气泡受污染后尾涡面积会增大,使气泡的阻力系数增加,进而降低气泡在静置液中的上升速度。
2.3.4=350~500时尾涡脱落情况随帽角的变化 圆球绕流的研究结果已表明,当280≤≤420时,涡开始脱落,但涡脱落的方向相同,仍然关于某一平面对称[31-32];当>420时,尾涡开始无规律脱落[32]。下文将在=350和=500这两种情况下,通过气泡尾部/=1处相差90°的两监测点:点(/=1、/=0.2、/=0)以及点(/=1、/=0.2、/=0)处3个方向上的速度随时间的变化来说明气泡界面变化对尾涡脱落情况的影响。两个监控点关于气泡的位置如图13所示,图中表示气泡直径,坐标原点位于气泡中心。
由于帽角0°~135°时气泡尾部存在尾涡,为对=350时不同帽角下尾涡发生脱落时的对称性进行讨论,图14给出了=350,帽角=0°、90°和135°时,气泡尾部两监测点处流向速度随时间的变化。可以看出:帽角=0°时,两监测点处流向速度波动的振幅相同,这说明涡环脱落的方向相同,尾涡关于某一平面对称,两监测点处流向速度波动的频率相同,这说明涡环呈周期性脱落;帽角=90°时,速度波动的振幅明显小于帽角=0°时速度波动的振幅,这说明此时脱落涡的强度已明显减弱;帽角=135°时,两监测点处流向速度没有出现波动,为恒定值,这说明污染程度较小的气泡,其尾部不会产生涡脱落现象。
由于帽角0°~135°时气泡尾部存在尾涡,为对=500时不同帽角下尾涡发生脱落时的对称性进行讨论,图15给出了=500,帽角=0°,90°和135°时,气泡尾部两监测点处流向速度随时间的变化。可以看出:当帽角=0°时,两监测点处流向速度波动振幅不同,这说明涡环脱落的方向不同,两监测点处流向速度波动频率不同,这说明涡环随机脱落,不再呈周期性脱落;当帽角=90°时,除了速度波动的振幅减弱外,还可以看出速度波动的随机性有所减小,这表示污染程度减小后尾涡脱落的频率与方向有趋向恒定的趋势。与=350时相同,当帽角=135°时,两监测点处流向速度波动消失,这表示污染程度较小的气泡,其尾部不会产生涡脱落现象。
3 结 论
本文使用计算流体力学法研究了气泡界面变化对其尾流的影响。借鉴圆球绕流和停滞帽模型,提出了一种模拟中等Reynolds数下受污染球形气泡尾流的三维简化模型,气泡界面污染程度取决于帽角的大小。研究发现,对于不同污染程度的气泡界面,其尾涡性质与尺寸也不同,具体结论如下。
(1)当=25~200时,随着帽角的增加,尾涡的面积会不断减小,当帽角≥157.5°时,尾涡将完全消失;对于尾涡尺寸,帽角的变化只会改变了尾涡相关尺寸(如尾涡长度、尾涡中心位置和尾涡的分离角)上数值上的大小,不会对其随Reynolds数的变化趋势造成影响。
(2)气泡受污染后尾涡面积会增大,使气泡的阻力系数增加,进而降低气泡在静置液中的上升速度,并将节约下来的动能被尾涡所消耗。
(3)当=250~500时,气泡表面污染程度的减小会使尾涡的三维特性减弱。
(4)当=350时,气泡表面污染程度的减小会使有序脱落的尾涡的强度减小并最终使其不发生脱落;当=500时,气泡表面污染程度的减小会使无规律脱落的尾涡的无序性减弱并最终使其不发生脱落。
符 号 说 明

CD——气泡阻力系数 Cp——压力系数 D——圆球域直径,m d——球形气泡直径,m Eo——Eötvös数 FD——阻力,N FDV——黏性力,N FDP——压力梯度力,N h——气泡中心到尾涡中心的距离,m Lre——所需边界层厚度,m Luse——气泡表面第一层网格的距离,m l——两尾涡中心的距离,m Ma——Marangoni数 Mo——Morton数 nx——法向单位矢量的流向分量 p——静压,Pa R——气体常数,J·mol-1·K-1 Re——雷诺数 S——气泡表面积,m2 s——尾涡长度,m T——温度,K t——时间,s Δt——时间步长,s U——进口液相速度,m·s-1 u——每个网格单元中的液相速度,m·s-1 ub——气泡运动速度,m·s-1 α——方位角,(°) Γ¥——气泡界面上的极限浓度,mol·kg-1 θ——帽角,(°) λ——气泡中心到进口或者壁面的距离,m μ——液相动力黏度,Pa·s ρ——液相密度,kg·m-3 τx——表面切应力流向分量,Pa φ——分离角,(°) 下角标 b——气泡 re——需求值 use——使用值 x——流向
References
[1] TASOGLU S, DEMIRCI U, MURADOGLU M. The effect of soluble surfactant on the transient motion of a buoyancy-driven bubble[J]. Phys. Fluids, 2008, 20(4): 65-79.
[2] ALKE A, BOTHE D. 3D numerical modeling of soluble surfactant at fluidic interfaces based on the VOF method[J]. FDMP, 2009, 5(4): 345-372.
[3] FLECHENSTEIN S, BOTHE D. Simplified modeling of the influence of surfactants on the rise of bubbles in VOF-simulations[J]. Chem. Eng. Sci., 2013, 102(5): 514-523.
[4] MURADOGLU M, TRYGGVASON G. Simulation of soluble surfactants in 3D multiphase flow[J]. J. Comput. Phys., 2014, 274: 737-757.
[5] 裴明敬, 朱婷婷, 杨晶晶, 等. 环境友好型生物表面活性剂对浮选气泡动力学的影响研究[J]. 高校化学工程学报, 2013, 27(6): 985-990. PEI M J, ZHU T T, YANG J J,. Study on effects of environment-friendly biosurfactants on bubble hydrodynamics in flotation column[J]. Journal of Chemical Engineering of Chinese Universities, 2013, 27(6): 985-990.
[6] 刘艳艳, 李彦鹏, 朱婷婷. 表面活性剂对中尺度气泡形状及速度的调控研究[J]. 西安交通大学学报, 2011, 45(10): 93-97. LIU Y Y, LI Y P, ZHU T T. Study on modulating shape and velocity of meso-scale bubble using surfactants[J]. Journal of Xi’an Jiaotong University , 2011, 45(10): 93-97.
[7] BHAGA D, WEDER M E. Bubbles in viscous liquids: shapes, wakes and velocities[J]. J. Fluid Mech., 1981, 105: 61-85.
[8] 倪明玖. 浮力作用下上升气泡的变形和驻涡形成机理研究[J]. 工程热物理学报, 2009, 30(1): 76-80. NI M J. Bubble rising driven by buoyancy with deformation and standing vortex[J]. Journal of Engineering Thermophysics, 2009, 30(1): 76-80.
[9] TRIPATHI M K, SAHU K C, GOVINDARAJAN R. Dynamics of an initially spherical bubble rising in quiescent liquid[J]. Nat. Commun., 2015, 6: 6268.
[10] GUMULYA M, JOSHI J B, UTIKAR R P,. Bubbles in viscous liquids: time dependent behaviour and wake characteristics[J]. Chem. Eng. Sci., 2016 , 144: 298-309.
[11] VELDHUIS C, BIESHEUWEL A, WIJNGAARDEN L V. Shape oscillations on bubbles rising in clean and in tap water[J]. Phys. Fluids, 2008, 20(4): 040705.
[12] SAITO T, TORIU M. Effects of a bubble and the surrounding liquid motions on the instantaneous mass transfer across the gas-liquid interface[J]. Chem. Eng. J., 2015, 265: 164-175.
[13] HUANG J, SAITO T. Influence of bubble-surface contamination on instantaneous mass transfer[J]. Chem. Eng. Technol., 2015, 38(11): 1947-1954.
[14] HUANG J, SAITO T. Influences of gas-liquid interface contamination on bubble motions, bubble wakes, and instantaneous mass transfer[J]. Chem. Eng. Sci., 2017, 157: 182-199.
[15] WANG Y P. A theoretical study of bubble motion in surfactant solutions[D]. Newark: New Jersey Institute of Technology, 1999.
[16] SADHAL S S, JOHNSON R E. Stokes flow past bubbles and drops partially coated with thin films. Part 1. Stagnant cap of surfactant film-exact solution[J]. J. Fluid Mech., 1983, 126: 237-250.
[17] FDHILA R B, DUINEVELD P C. The effect of surfactant on the rise of a spherical bubble at high Reynolds and Peclet numbers[J]. Phys. Fluids, 1996, 8(2): 310-321.
[18] CUENOT B, MAGNAUDET J, SPENNATO B. The effects of slightly soluble surfactants on the flow around a spherical bubble[J]. J. Fluid Mech., 1997, 339: 25-53.
[19] PALAPARTHI R, PAPAGEORGIOU D. Theory and experiments on the stagnant cap regime in the motion of spherical surfactant-laden bubbles[J]. J. Fluid Mech., 2006, 559: 1-44.
[20] DUKHINA S S, KOVALCHUKB V I, GOCHEVCD G G,. Dynamics of rear stagnant cap formation at the surface of spherical bubbles in surfactant solutions at large Reynolds numbers under conditions of small Marangoni number and slow sorption kinetics[J]. Adv. Colloid Interface Sci., 2015, 222: 260-274.
[21] DUKHINA S S, LOTFIBC M, KOVALCHUKB V I,. Dynamics of rear stagnant cap formation at the surface of rising bubbles in surfactant solutions at large Reynolds and Marangoni numbers and for slow sorption kinetics[J]. Colloid Surface A, 2016, 492: 127-137.
[22] FLECHENSTEIN S, BOTHE D. Simplified modeling of the influence of surfactants on the rise of bubbles in VOF-simulations[J]. Chem. Eng. Sci., 2013, 102(5): 514-523.
[23] GANESAN S, TOBISKA L. Arbitrary Lagrangian-Eulerian finite-element method for computation of two-phase flows with soluble surfactants[J]. J. Comput. Phys., 2012, 231: 3685-3702.
[24] FUJIOKA H. A continuum model of interfacial surfactant transport for particle methods[J]. J. Comput. Phys., 2013, 234: 280-294.
[25] KHATRI S, TORNBERG A K. An embedded boundary method for soluble surfactants with interface tracking for two-phase flows[J]. J. Comput. Phys., 2014, 256: 768-790.
[26] MITTAL R, NAJJAR F M. Vortex dynamics in the sphere wake[C]// 30th Fluid Dynamics Conference, Fluid Dynamics and Co-located Conferences, Norfolk: AIAA J., 1999: 1-8.
[27] TOMBOULIDES A G, ORSZAG S A. Numerical investigation of transitional and weak turbulent flow past a sphere[J]. J. Fluid Mech., 2000, 416: 45-73.
[28] KIM H J, DURBIN P A. Observations of the frequencies in a sphere wake and of drag increase by acoustic excitation[J]. Phys. Fluids, 1988, 31(11): 3260-3265.
[29] 张鸣远, 景思睿, 李国君. 高等工程流体力学[M]. 北京: 高等教育出版社, 2012. ZHANG M Y, JING S R, LI G J. Advanced Engineering Fluid dynamics[M]. Beijing: Higher Education Press, 2012.
[30] CROWE C T, SCHWARZKOPF J D, SOMMERFELD M,. Multiphase Flows with Droplets and Particles[M]. Boca Raton: Chemical Rubber Company Press, 2012.
[31] NATARAJAN R, ACRIVOS A. The instability of the steady flow past spheres and disks[J]. J. Fluid Mech., 1993, 254(1): 323-344.
[32] SAKAMOTO H, HANJU H. The formation mechanism and shedding frequency of vortices from a sphere in uniform shear flow[J]. J. Fluid Mech., 1995, 287: 151-171.
[33] MAGARVEY R H, MACLATCHY C S. Vortices in sphere wakes[J]. Can. J. Phys., 1965, 43: 1649-1656.
[34] MEI R, KLAUSNER J F, LAWRENCE C J. A note on the history force on a spherical bubble at finite Reynolds number[J]. Phys. Fluids, 1994, 6(1): 418-420.
[35] MEI R. History force on a sphere due to a step change in the free-stream velocity[J]. Int. J. Multiphase Flow, 1993, 19: 509-525.
[36] TASOGLU S, DEMIRCI U, MURADOGLU M. The effect of soluble surfactant on the transient motion of a buoyancy-driven bubble[J]. Phys. Fluids, 2008, 20(4): 65-79.
[37] TAKAGI S, OGASAWARA T, MATSUMOTO Y. The effect of surfactant on the multiscale structure of bubbly flows[J]. Phil. Trans. R. Soc. A, 2008, 366: 2117-2129.
[38] TANEDA S. Experimental investigation of the wake behind a sphere at low Reynolds number[J]. J. Phys. Soc. Jpn., 1956, 11(10): 1104-110.
Influence of interface change for spherical bubble on vortex characteristic and size
FEI Yang, PANG Mingjun
(Jiangsu Key Laboratory of Green Process Equipment, School of Mechanical Engineering, Changzhou University, Changzhou 213164, Jiangsu, China)
The numerical method is employed to investigate the influence of contaminated degree of bubble surface on its wakes for the spherical bubble under moderate Reynolds number (25≤≤500). By referencing the flow past a sphere and the stagnant cap model, one kind of three-dimensional model for contaminated spherical bubble under moderate Reynolds number is proposed.The interface contaminated degree is dependent on the magnitude of the cap angle. The larger the cap angel is, the slighter the bubble interface pollution is. The present results show that, for 25≤≤200, the magnitudes of the vortex length, the vortex center position distance to the bubble rear and the separation angle decrease with the decrease of the bubble surface contaminated degree but the distribution trends of those parameters against the Reynolds number are similar; for 250≤≤500, the decrease of the bubble surface contaminated degree weakens the three-dimensional property of vortexes, reduces the strength of orderly shedding vortexes until the shedding phenomenon disappears at=350, and reduces the disorder of shedding vortexes until the shedding phenomenon disappears too at=500.
bubble; interface; wake; laminar flow; hydrodynamics
10.11949/j.issn.0438-1157.20170290
O 357.1
A
0438—1157(2017)09—3409—11
2017-03-23收到初稿,2017-06-27收到修改稿。
庞明军。
费洋(1994—),男,硕士研究生。
国家自然科学基金项目(51376026);江苏省青蓝工程项目。
2017-03-23.
Prof. PANG Mingjun, pangmj@cczu.edu.cn
supported by the National Natural Science Foundation of China (51376026) and the Qinglan Project of Jiangsu Province.

