二项式分布在种群平衡模型模拟粒度分布中的应用

李振亮，卢培利，张代钧，周志恩，张晟，何强



二项式分布在种群平衡模型模拟粒度分布中的应用

李振亮1,2，卢培利3,4，张代钧3,4，周志恩2，张晟2，何强1,5

（1重庆大学城市建筑与环境工程学院，重庆400044；2重庆市环境科学研究院，重庆401147；3重庆大学煤矿灾害动力学与控制国家重点实验室，重庆400044；4重庆大学环境科学系，重庆400044；5重庆大学三峡库区生态环境教育部重点实验室，重庆400044）

提出了一种适用于几何网格的子粒子二项式分布函数，并应用于种群平衡模型模拟活性污泥絮凝后的粒度分布。结果表明：与二元分布相比，该二项式分布可以得到更准确的粒度分布和平均粒度模拟值；通过校核二项式分布参数C的取值，可以提高粒度分布和平均粒度的模拟精度。相比于二元分布或正态分布只能描述一种类型的子粒子分布，该二项式分布具有较强的适应性，调整参数C的取值，可以得到更多可能的子粒子分布；参数C还可以表征粒子的破碎方式——较小的C值表征粒子具有较强的稳定性，易破碎生成较大的子粒子；较大的C值表征粒子具有较弱的稳定性，易破碎生成较小的子粒子。

种群平衡；二项式分布；粒度分布；数值模拟；破碎；子粒子

引 言

种群平衡模型（population balance model，PBM）是描述多相流体系中分散相大小分布的重要方法，在结晶体系、絮凝体系、粒子或气泡形成体系中得到了广泛应用[1-5]。应用种群平衡模型描述絮凝动力学，分析粒子聚并和破碎行为对粒度分布的影响，有助于更好地认识絮体粒子的形成、演变及运动规律[6-11]。

粒子可通过侵蚀（小粒子从大粒子表面侵蚀脱落）和破裂（大粒子分裂成两个或更多较小的粒子）等方式发生破碎[12-13]，进而形成不同的子粒子分布[14]。由于难于实测子粒子分布规律，以往的种群平衡模型中一般采用假设的子粒子分布函数，如二元分布（binary distribution）、三元分布（ternary distribution）和高斯分布（Gaussian distribution）[15-16]。其中，假设粒子破裂生成两个等大子粒子的二元分布应用最为广泛，而高斯分布认为粒子破裂生成子粒子的概率密度符合高斯分布。值得注意的是，这些子粒子分布函数只能描述一种类型的子粒子分布，并不能描述其他可能的子粒子分布。

另外，如果应用离散区间法求解种群平衡模型，上述子粒子分布的应用还需结合计算网格，如二元分布多应用于几何网格v=2v-1，高斯分布多应用于均匀网格（v=，为常数），且可近似为二项分布[17-18]

式中，v为粒子的体积，γ为粒子破碎为子粒子的分布函数。根据式（1），粒子（体积为，以下简称）破碎后生成两个等大子粒子（2）的发生概率最大。种群平衡模型求解中，划分网格的数量直接决定了计算量[19-20]；式（1）虽然简化了高斯分布的计算，但是均匀网格对应的计算量较大（尤其是粒子粒度范围较大时），从而限制了式（1）或高斯分布的应用。

本文提出了一种适用于几何网格、能够描述粒子破碎后子粒子多种可能分布的二项式分布函数，并将其应用于种群平衡模型对活性污泥絮凝动力学的模拟，通过对絮体粒子粒度分布和平均粒度模拟结果的对比，分析其适用性和优越性。

1 模型与方法

1.1 种群平衡模型

描述粒子在聚并或破碎后的数量浓度变化率的种群平衡模型为[21]

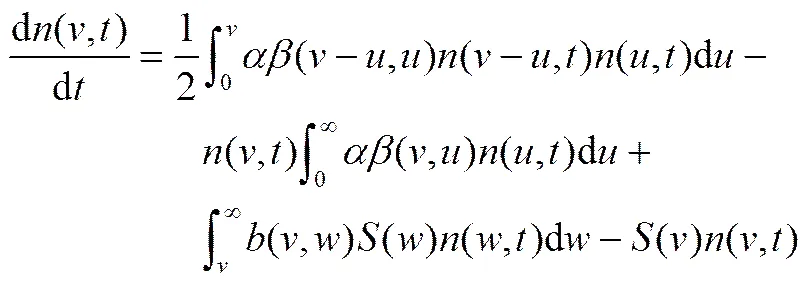
式（2）右边第1、2项分别为由于粒子聚并产生的生成项和消亡项，第3、4项分别为由于粒子破碎产生的生成项和消亡项；其中，为粒子（）的数量浓度,为聚并效率，()为粒子（）和粒子（）间的碰撞频率，()为粒子（）破碎为粒子（）的概率密度函数，()为粒子（）的破碎速率。

应用离散区间法，式（2）可转化为离散的种群平衡模型[22]

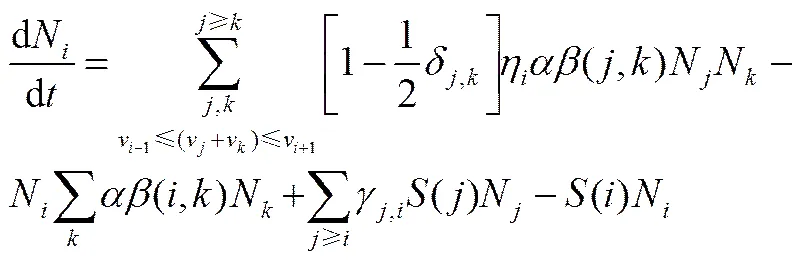
式中，N为粒子数量浓度，δ,k为Dirac Delta函数，η为分配系数

(4)

聚并效率通常被视作0～1的常数或者与粒度相关的函数[8,23-25]，可通过模型校核来确定。由于粒子的聚并和破碎是同时发生的，所以聚并效率和破碎速率系数往往同时进行校核确定[24,26]。碰撞频率和破碎速率与粒度相关，考虑粒子间作用更依赖于粒子的最大粒度[27]。因此，碰撞频率和破碎速率可分别描述为[28]

() =c()(6)

式（5）中，为速度梯度（本文只考虑了流体剪切引起的碰撞频率），c为最大粒度；式（6）中为破碎速率系数。最大粒度c与等效粒度L的关系可近似为[28]

式中，P为基本粒度，2为二维分形维数。

1.2 子粒子分布函数

假设粒子均由基本粒子构成，所含基本粒子的数量可以代表粒子的类别[29]。以几何网格（v=2v-1）为例，粒子类别如图1所示。

只考虑粒子破碎生成两个子粒子的情况，以粒子（P= 8）的破碎为例，存在4种破碎方式（图2）。

图2中，粒子（P= 3，5，6，7）被按比例分配至相邻的粒子类别中；如1个P= 3的粒子可分配为1/2个P= 2的粒子和1/2个P= 4的粒子。假设4种破碎方式的概率相同，可计算出粒子破碎为子粒子的数量分布（表1）。

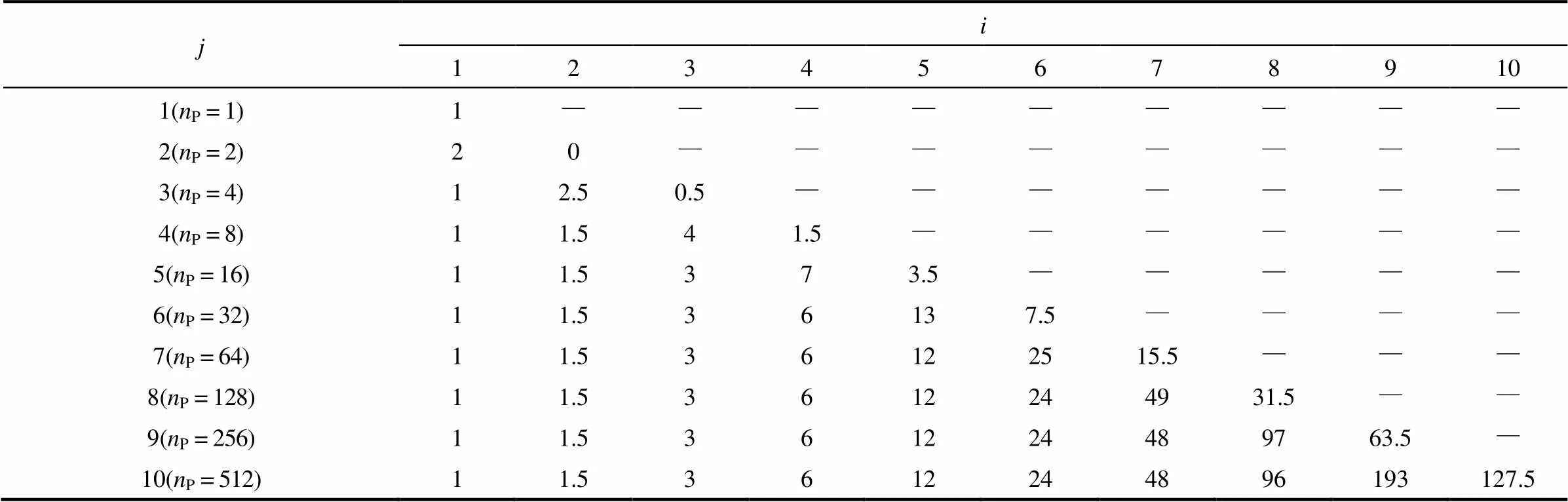
表1 粒子j破碎为子粒子i的数量分布

由表1可见，子粒子的生成概率符合一定的分布规律，即体积为原粒子体积1/2的子粒子的生成概率最大，如粒子（= 4）破碎后生成子粒子（= 3）的概率最大。将表1的子粒子数量分布归一化处理后，子粒子概率分布可以较好地被二项式分布函数来描述（图3）；该二项式分布函数为

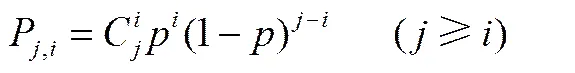
式中，P为粒子破碎为子粒子的生成概率，为参数。由二项式分布定义可知，如果子粒子-1的生成概率最大，则×=-1。

图3 二项式分布函数的子粒子概率分布模拟结果

Fig.3 Simulated probability distribution of daughter particles by binomial distribution function

○ analysis results; —— simulation results

已知生成概率P，则子粒子分布函数为

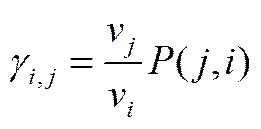
以上分析是以特定几何网格（v=2v-1）划分粒子类别为例，对于一般情形（v=kv1，1<<2），可以通过定义参数C来决定发生概率的分布

= (-C)/(10)

如果粒子（）破碎后子粒子（/2）的生成概率最大，则

C= lg2/lg(11)

1.3 参数校核

种群平衡模型的最终状态是粒子的聚并与破碎达到平衡，即式（3）中dN/d= 0。将式（6）代入式（3），得

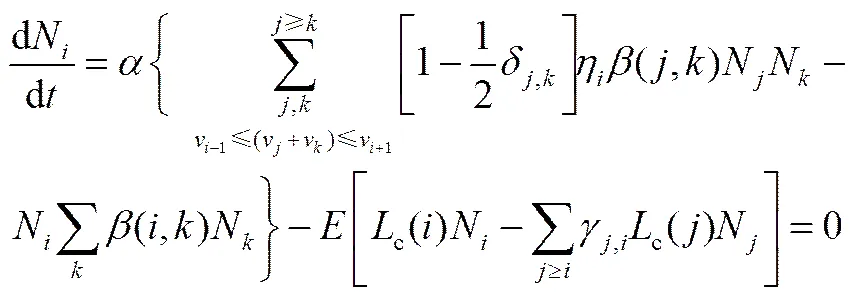
由式（12）可见，当粒度分布（数量浓度）一定时，聚并效率与破碎速率系数之比是唯一且可确定的值。

参数校核采用最小误差法，定义

式中，为粒子类别总数，()和′() 分别为粒子体积分数的实测值和模拟值。

定义

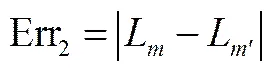
式中，L和L分别为平均粒度的实测值和模拟值

(15)

式中，V为粒子总体积。

1.4 实测数据

采用活性污泥絮凝后的粒度分布实测数据（= 28.2 s-1）进行模型验证与参数校核。活性污泥取自城市污水处理厂，粒度分布采用激光粒度分析仪S3500（Microtrac, Enhanced型号）测量，粒子二维分形维数采用显微图像分析法测量[28,30]。通过S3500测量得到的累计体积分数可插值得到不同粒度粒子的体积分数，即某类粒子总体积（V）与所有类别粒子的总体积（V）之比。种群平衡模型描述的是粒子数量浓度（N），因此需要建立V与N之间的关系[7]

其中

(17)

式中，T为样本总体积；为样本浓度；f为絮体密度；为絮体中液相与固相之比

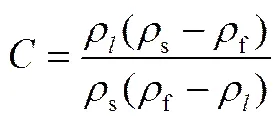
式中，ρ和s分别为液相和固相的密度。

本研究中，活性污泥样本浓度为0.1 kg·m-3，ρ、s和f分别为1000、1040、1700 kg·m-3。

2 结果与讨论

图4为二项式分布和二元分布所对应的粒度分布模拟结果，参数校核结果见表2。当≠ 2时，二元分布的处理思路是：假设破碎生成两个等大的子粒子，参考式（4）的分配方法计算出相应类别粒子的分配比例值，并将该分配比例值视作生成概率。由图4可见，二项式分布与二元分布对应的模拟曲线形状有差异，说明子粒子分布对粒度分布模拟结果有影响。

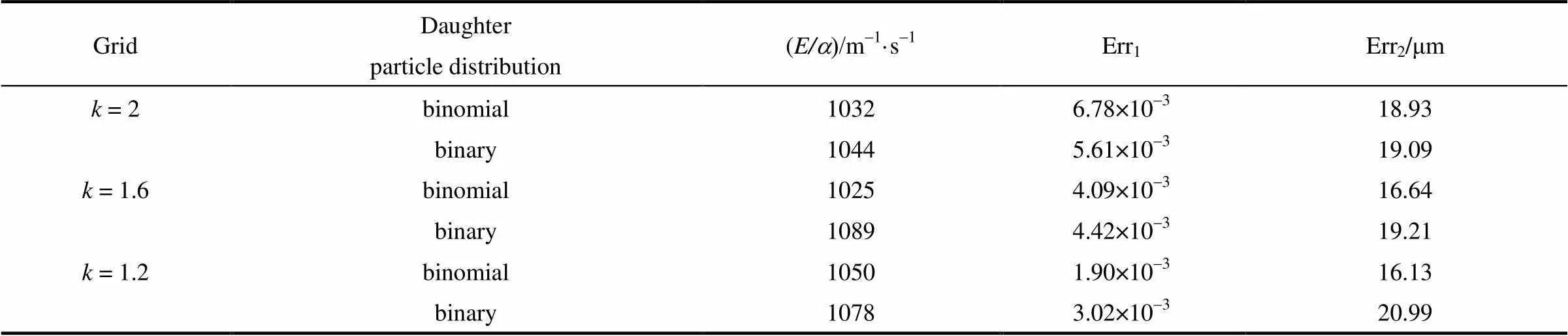
表2 二项式分布和二元分布对应的参数校核结果

表2中，二项式分布与二元分布对应的参数校核结果差异不显著，与文献[3]的结论一致。原因可能在于采用式（10）、式（11）计算的二项式分布结果中粒子破碎生成两个等大子粒子的发生概率最大，与二元分布结果类似。无论是二项式分布，还是二元分布，离散区间划分网格数量越多（值越小），粒度分布模拟误差越小。相比于二元分布，二项式分布对粒度分布和平均粒度的模拟误差更小（= 2.0的粒度分布模拟例外）。

二项式分布中，按照式（11）计算参数C的前提假设是粒子破碎方式（图2）的发生概率相同。如果破碎方式的发生概率不同（如更倾向于侵蚀破碎或者完全破裂），C的值可能会发生变化。

分别选取3种不同的活性污泥（取自不同的培养阶段，有机质含量不同），测得粒度分布差异明显，“中心位置”和“形状”均不同（图5）。本文采用两种不同的二项式分布处理方法对粒度分布进行了模拟，图5（a）中，方法1[C为定值，由式（11）计算]较好地模拟了粒度分布“中心位置”的变化，但是对于“形状”变化的模拟结果不理想；图5（b）显示，方法2（C为模型校核参数）较好地模拟了粒度分布“中心位置”和“形状”的变化，粒度分布和平均粒度的模拟结果误差更小（表3）。由此可见，二项式分布具有较强的适应性，通过调整二项式分布参数C的取值，可以提高粒度分布和平均粒度的模拟精度。

表3 不同活性污泥粒度分布对应的模型参数校核结果

二项式分布参数C的取值还可以反映粒子的破碎方式。表3中，方法1中由式（11）计算得到的C= 1.47，表示粒子（）破碎后生成两个等大子粒子（）的发生概率最大。C< 1.47表示粒子（）破碎生成子粒子（介于/2和之间）的发生概率最大；C>1.47表示粒子（）破碎生成子粒子（介于0和/2）的发生概率最大（图6）。较小的C值意味着粒子具有较强的稳定性，破碎后易生成较大的子粒子；反之，较大的C值意味着粒子具有较弱的稳定性，破碎后易生成较小的子粒子。表3中，方法2校核得到的C值为0.97～1.78，活性污泥絮凝机理[31-32]与该值代表意义相符：当活性污泥EPS含量较低时，不易絮凝形成较大的絮体，而且絮体稳定性较强，对应C的值较小；当活性污泥粒子EPS含量较高时，易絮凝形成较大的絮体，但是形成的絮体稳定性较差，破碎易生成为较小的子絮体，对应C的值较大。

3 结 论

（1）提出的二项式分布函数[式（8）、式（10）、式（11）]适合于几何网格，能够描述粒子破碎后的子粒子分布；且具有较强的适应性，通过调整参数C的取值，得到可能更符合特定对象实际的子粒子分布。

（2）按式（11）计算参数C，可得到等大子粒子生成概率最大的二项式分布；将其应用于种群平衡模型模拟活性污泥絮凝动力学，与传统的二元分布相比，可以得到更准确的粒度分布和平均粒度模拟结果。

（3）针对不同活性污泥粒度分布差异明显的情况，通过校核二项式分布参数C的取值，可以提高粒度分布和平均粒度的模拟精度；校核所得的参数C的取值还可以反映粒子的破碎方式，较小的C值表明粒子具有较强的稳定性，破碎易生成较大的子粒子；较大的C值表明粒子具有较弱的稳定性，破碎易生成较小的子粒子。

符 号 说 明

b(v,w)——粒子破碎的概率密度函数 Cp——二项式分布参数 D2——二维分形维数 E——破碎速率系数，m-1·s-1 Err1——粒度分布的平均误差 Err2——平均粒度的平均误差 G——平均速度梯度，s-1 L——粒子等效粒度，μm Lc——粒子最大粒度，μm Lm——粒子平均粒度，μm LP——基本粒度，μm m(i)——粒子体积分数 Ni——粒子i的数量浓度，m-3 n——粒子种类数量 Pj,i——粒子j破碎为子粒子i的生成概率 p——参数 S(i)——粒子i的破碎速率，s-1 Vf——所有类别粒子的总体积，m3 Vi——粒子 i的总体积，m3 VT——样本总体积，m3 vi——粒子i的体积，m3 X——样本浓度，kg·m-3 α——聚并效率 β(i,j)——粒子i和粒子j间的碰撞频率，m3·s-1 γj,i——粒子j破碎为子粒子i的分布函数 δj,k——Dirac Delta函数 ηi——分配系数 ρf——絮体密度，kg·m-3 ρl——液相密度，kg·m-3 ρs——固相密度，kg·m-3

References

[1] 郑建祥, 许帅, 王京阳,等. 基于微分代数积分矩量法的聚并器超细粒子聚团研究[J]. 化工学报, 2017, 68(1): 119-128. ZHENG J X, XU S,WANG J Y,Simulation of ultrafine particle aggregation in aggregation device by differential-algebraic quadrature method of moments[J]. CIESC Journal, 2017, 68(1): 119-128.

[2] 王铁峰. 气液-浆-反应器流体力学行为的实验研究和数值模拟[D]. 北京: 清华大学, 2004. WANG T F. Experimental study and numerical simulation on the hydrodynamics in gas-liquid (slurry) reactors [D]. Beijing: Tsinghua University, 2004.

[3] BRIESEN H. Simulation of crystal size and shape by means of a reduced two-dimensional population balance model[J]. Chemical Engineering Science, 2006, 61(1): 104-112.

[4] LEE K F, DOSTA M, MCGUIRE A D,Development of a multi-compartment population balance model for high-shear wet granulation with discrete element method[J]. Computers & Chemical Engineering, 2017, 99: 171-184.

[5] WANG B, MOSBACH S, SCHMUTZHARD S,Modelling soot formation from wall films in a gasoline direct injection engine using a detailed population balance model[J]. Applied Energy, 2016, 163: 154-166.

[6] DUCOSTE J. A two-scale PBM for modeling turbulent flocculation in water treatment processes[J]. Chemical Engineering Science, 2002, 57(12): 2157-2168.

[7] NOPENS I, KOEGST T, MAHIEU K,PBM and activated sludge flocculation: from experimental data to calibrated model[J]. AIChE Journal, 2005, 51(5): 1548-1557.

[8] DING A, HOUNSLOW M J, BIGGS C A. Population balance modelling of activated sludge flocculation: investigating the size dependence of aggregation, breakage and collision efficiency[J]. Chemical Engineering Science, 2006, 61(1): 63-74.

[9] YEOW Y L, LIOW J, LEONG Y. A general procedure for obtaining the evolving particle-size distribution of flocculating suspensions[J]. AIChE Journal, 2012, 58(10): 3043-3053.

[10] JELDRES R I, CONCHA F, TOLEDO P G. Population balance modelling of particle flocculation with attention to aggregate restructuring and permeability[J]. Advances in Colloid & Interface Science, 2015, 224: 62.

[11] LI Z L, LU P L, ZHANG D J,Population balance modeling of activated sludge flocculation: investigating the influence of extracellular polymeric substances (EPS) content and zeta potential on flocculation dynamics[J]. Separation & Purification Technology, 2016, 162: 91-100.

[12] JARVIS P, JEFFERSON B, GREGORY J,A review of floc strength and breakage[J]. Water Research, 2005, 39(14): 3121–3137.

[13] YUAN Y, FARNOOD R R. Strength and breakage of activated sludge flocs[J]. Powder Technology, 2010, 199(2): 111-119.

[14] SCHUETZ S, PIESCHE M. A model of the coagulation process with solid particles and flocs in a turbulent flow[J]. Chemical Engineering Science, 2002, 57(20): 4357-4368.

[15] SPICER P T, PRATSINIS S E. Coagulation and fragmentation: universal steady-state particle-size distribution[J]. AIChE Journal, 1996, 42(6): 1612-1620.

[16] ZHANG J J, LI X Y. Modeling particle-size distribution dynamics in a flocculation system[J]. AIChE Journal, 2003, 49(7): 1870-1882.

[17] SERRA T, CASAMITJANA X. Modelling the aggregation and break-up of fractal aggregates in a shear flow[J]. Flow, Turbulence and Combustion, 1997, 59(2): 255-268.

[18] MAGGI F, MIETTA F, WINTERWERP J C. Effect of variable fractal dimension on the floc size distribution of suspended cohesive sediment[J]. Journal of Hydrology, 2007, 343(1): 43-55.

[19] 苏军伟, 顾兆林, XU X Y. 离散相系统种群平衡模型的求解算法[J]. 中国科学: 化学, 2010, 40(2): 144-160. SU J W, GU Z L, XU X Y. Advances of solution methods of population balance equation for disperse phase system[J]. Scientia Sinica Chimica, 2010, 40(2): 144-160.

[20] LI Z L, ZHOU Z E, ZHANG S,Comparison of the accuracy and performance of different numbers of classes in discretised solution method for population balance model[J]. International Journal of Chemical Engineering, 2016, 2: 1-6.

[21] RAMKRISHNA D. Population Balances: Theory and Applications to Particulate Systems in Engineering[M]. London: Academic Press, 2000.

[22] KUMAR S, RAMKRISHNA D. On the solution of population balance equations by discretization(Ⅱ): A fixed pivot technique[J]. Chemical Engineering Science, 1996, 51(8): 1311-1332.

[23] THOMAS D N, JUDD S J, FAWCETT N. Flocculation modelling: a review[J]. Water Research, 1999, 33(7): 1579-1592.

[24] LI X Y, LOGAN B. Collision frequencies between fractal aggregates and small particles in a turbulently sheared fluid[J]. Environmental Science & Technology, 1997, 31(4): 1237-1242.

[25] BIGGS C A, LANT P A. Modelling activated sludge flocculation using population balances[J]. Powder Technology, 2002, 124(3): 201-211.

[26] MIETTA F, CHASSAGNE C, VERNEY R,On the behavior of mud floc size distribution: model calibration and model behavior[J]. Ocean Dynamics, 2011, 61(2): 257-271.

[27] FLESCH J C, SPICER P T, PRATSINIS S E. Laminar and turbulent shear‐induced flocculation of fractal aggregates[J]. AIChE Journal, 1999, 45(5): 1114-1124.

[28] LI Z L , ZHANG D J, LU P L,Population balance model and calibration method for simulating the time evolution of floc size distribution of activated sludge flocculation[J]. Desalination and Water Treatment, 2017, 67: 41-50.

[29] MAGGI F. Flocculation dynamics of cohesive sediment[D]. Delft : Delft University of Technology, 2005.

[30] 李振亮, 张代钧, 卢培利,等. 活性污泥粒度分布与分形维数的影响因素[J]. 环境科学, 2013, 34(10): 3975-3980. LI Z L, ZHANG D J, LU P L,Influencing factors of floc size distribution and fractal dimension of activated sludge[J]. Environmental Science, 2013, 34(10): 3975-3980.

[31] WILEN B M, JIN B, LANT P. The influence of key chemical constituents in activated sludge on surface and flocculating properties[J]. Water Research, 2003, 37(9): 2127-39.

[32] SHENG G P, YU H Q, LI X Y. Extracellular polymeric substances (EPS) of microbial aggregates in biological wastewater treatment systems: a review[J]. Biotechnology Advances, 2010, 28(6): 882-894.

Application of binomial distribution for daughter particles in simulation of particle size distribution by population balance model

LI Zhenliang1,2, LU Peili3,4, ZHANG Daijun3,4,ZHOU Zhi’en2, ZHANG Sheng2, HE Qiang1,5

(1College of Urban Construction and Environmental Engineering, Chongqing University, Chongqing 400044, China;2Chongqing Research Academy of Environmental Sciences, Chongqing 401147, China;3State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China;4Department of Environmental Science, Chongqing University, Chongqing 400044, China;5Key Laboratory of the Three Gorges Reservoir Region’s Eco-environment, Ministry of Education, Chongqing University, Chongqing 400045, China)

A binomial distribution function suitable for geometric grid was proposed and applied in population balance model (PBM) to simulate the particle size distribution (PSD) of activated sludge after flocculation. The results showed that the PSD and mean size simulated by using binomial distribution give better agreement with the experimental data than those simulated by using binary distribution. The accuracy of simulation of PSD and mean size can be improved by calibrating the value of parameterCof binomial distribution function. Different from other daughter particle distribution which can only describe one-type daughter particle distribution, the binomial distribution function shows a strong adaptability and can present more probable daughter particle distributions through adjusting the parameterC. Moreover, the value of parameterCmight also characterize breakage behavior of particle: a smallerCvalue might imply that the particle display strong stability leading to large numbers of large daughter particle, whereas a largerCvalue might imply that the particle display weak stability and the large-scale fragmentation resulting in large numbers of small daughter particle.

population balance; binomial distribution; particle size distribution; numerical simulation; breakage; daughter particle

10.11949/j.issn.0438-1157.20170675

TQ 028.5

A

0438—1157（2017）09—3397—07

2017-05-25收到初稿，2017-06-29收到修改稿。

卢培利。

李振亮（1981—），男，博士，副教授。

国家自然科学基金项目（5160091049）；重庆市科委专项基金项目（2015CSTC-JBKY-01605）；重庆市基础科学与前沿技术研究专项项目（CSTC2016jcyjA0506）。

2017-05-25.

Prof.LU Peili, lupl@cqu.edu.cn

supported by the National Natural Science Foundation of China (5160091049), the Natural Science Foundation of Chongqing (2015CSTC-JBKY-01605) and the Chongqing Research Program of Basic Research and Frontier Technology(CSTC2016jcyjA0506).