汽轮机动叶栅顶部通道湿蒸汽超声速凝结流动特性

韩旭，韩中合



汽轮机动叶栅顶部通道湿蒸汽超声速凝结流动特性

韩旭，韩中合

（华北电力大学电站设备状态监测与控制教育部重点实验室，河北保定071003）

由于汽轮机内高速凝结流动的复杂性，目前还没有一个得到普遍公认的凝结成核模型，且现有数值模型通常忽略汽液相间滑移。针对叶栅通道内凝结参数分布陡峭、变化敏感的特点，采用既能准确描述可压缩气体跨声速流动又能捕捉参数突跃的双流体数值模型，对汽轮机动叶栅顶部通道内的凝结流动特性进行分析。揭示压比对湿蒸汽非平衡凝结特性的影响，归纳了叶片表面压力、成核率、湿度、水滴数的变化规律。研究表明：各工况压力面的压比计算值与实验数据吻合较好，但吸力面后半段存在一定误差；双流体数值模型适用于过热工况和入口过冷度较小的凝结工况，但当入口过冷度较大时，几乎无法捕捉到凝结激波导致的压力突跃；激波干涉和涡团掺混也会对水滴分布产生较大影响。

湿蒸汽；汽轮机；超声速；两相流；凝结；热力学

引 言

湿蒸汽非平衡凝结现象广泛存在于化工机械、动力机械等领域，高速流动的水蒸气需要达到某个过饱和状态后才开始出现凝结。非平衡凝结流动中涉及的成核和水滴生长数学理论被列为21世纪100道科学难题之一[1]。火电汽轮机末几级及核电汽轮机全部级都处于湿蒸汽区，随着蒸汽湿度的增加，湿蒸汽给汽轮机带来两方面的问题：一是产生较大的湿汽损失，使湿蒸汽级的效率明显低于干蒸汽级；二是湿蒸汽中的水分会对汽轮机动叶产生侵蚀与冲击，威胁汽轮机的安全运行[2-3]。提高蒸汽循环效率的主要途径为提高蒸汽参数和降低背压，目前一些机组的设计背压在4 kPa以下，超低背压使汽轮机的排汽湿度增大，湿蒸汽问题更显突出。因此，研究汽轮机内湿蒸汽问题对我国电力行业发展具有重要的理论与现实意义。

汽轮机内的蒸汽凝结流动是三维黏性非定常、具有间断面激波和气液两相共存的复杂非平衡流动，主要涉及湍流、激波与附面层干扰、边界层状态变化、凝结激波与气动激波相互干涉等复杂物理问题。在国外，比利时冯•卡门流体力学研究所[1]、英国中央电业研究实验室[2]、莫斯科动力学院[3]、伯明翰大学[4-5]、剑桥大学[6-7]等机构开展了湿蒸汽两相流的计算与测量工作，在凝结理论、实验研究、解析分析及数值模拟等方面取得了很多成果。在国内，西安交通大学[8-12]、清华大学[13-14]、中国科学院工程热物理研究所[15-16]、哈尔滨工业大学[17-18]、华北电力大学[19-24]等在凝结理论、实验研究及数值模拟等方向开展了很多工作。总之，汽轮机内湿蒸汽两相流动研究发展较快，基础性的工作已经比较完善，尚存在一些问题亟待解决。第一，还没有一个得到普遍公认的凝结成核模型。尽管经典成核模型得到了很广泛的应用，但是仍存在一定偏差。经典成核理论认为水滴温度与汽相温度相同，并没有考虑相变产生的凝结潜热，这显然与实际情况不符。部分文献采用非等温修正模型计算成核率，然而修正系数取值范围很大，导致成核率计算值甚至存在数量级上的差异。第二，水滴生长理论还存在一定缺陷。汽轮机中凝结流动研究的大多数水滴处于低压过渡区，但目前很少有文献涉及过渡区的水滴生长过程研究。第三，现有数值模型通常忽略汽液相间滑移。求解三维凝结流动Eulerian法更具优势，但由于计算机水平或者计算时间的限制，此方法通常忽略汽液相间滑移。

本文通过对经典均质成核理论进行推导和总结，采用适应性强的非等温修正成核模型，建立了考虑相间作用及湍流影响的双流体数值模型，对汽轮机动叶顶部通道湿蒸汽凝结流动特性进行分析，并根据Bakhtar实验结果验证了本文计算模型的准确性。讨论了压比、进口过冷度对水蒸气非平衡凝结特性的影响，归纳了叶栅内成核率、湿度、水滴数的变化规律。研究结果可为汽轮机通流部分结构优化设计提供科学依据与参考。

1 模型构建

1.1 成核及水滴生长模型

经典成核模型并未考虑凝结潜热对流动的影响，其成核率计算式为[1]

非等温修正模型将凝结潜热的影响考虑进来，其计算式为[2]

(2)

尽管非等温修正模型计算结果和实验值吻合较好，但是在温度较低时仍存在一定偏差。Wölk等[25]通过分析低温实验数据，构造经验函数成核模型，具体形式为

该模型主要根据一定范围内水蒸气成核率实验数据外推得到的，因此其适用范围有待进一步验证。当蒸汽温度一定时，各种成核模型的-曲线斜率十分相似，这说明各种成核模型的主要影响因素为蒸汽温度，但这种影响很难在-图上体现。因此，本文绘制-g曲线（图1）用于研究给定成核率下温度对过饱和度的影响。图1中的实验数据取自文献[26-27]。

图1 定成核率下过饱和度计算结果

Fig. 1 Calculation results of saturation degree at constant nucleation rate

研究表明：当饱和温度在230～290 K范围内时，Wölk-Strey成核率和非等温成核率计算值与实验值的吻合度更好；当饱和温度高于290 K后，3种成核模型过饱和度曲线基本重合。鉴于汽轮机末级内的湿蒸汽流动，成核过程温度约为320～340 K，因此选择3种成核模型进行计算都是合理的，本文选择非等温修正成核率模型。

水分子与凝结核的撞击频率与水滴半径及气体分子平均自由程有关，引进量纲1参数Knudsen数（）衡量撞击频率。水滴生长过程采用Young等[28]非等温低压修正模型进行描述。

1.2 双流体数值模型

湿蒸汽是由大量蒸汽分子和微小水滴组成的混合物，为了简化计算对其进行如下假设[4-5]。

（1）将液相视为连续性介质，具有连续的速度、温度、水滴数分布，汽液两相具有不同的速度；

（2）忽略水滴的旋转、碰撞、聚合和电荷特性；

（3）忽略扩大水滴表面积所做的功，不计水滴在叶片表面的沉积；

（4）流体为各向同性牛顿流体，流场中无热源且与外界绝热。

将湿蒸汽凝结过程孤立为一个黑箱，将汽液两相近似为与环境存在质量、动量、能量交换的开口系统[8-10]。在此基础上，建立湿蒸汽凝结流动双流体数值模型，如图2所示。

汽相模块的作用是提供时刻的流动参数g、、、；液相模块将液相参数、、d传递给成核及水滴生长模块。成核及水滴生长模块通过流动参数计算出质量凝结速率、凝结潜热fg，并将其反馈到汽相模块、液相模块，作为连续性方程、动量方程、能量方程的源相。由控制方程计算出水滴数目、湿度分布。随后进行+1时刻的凝结流动计算。

与单流体模型相比，双流体模型考虑了相间滑移引起的动量交换对凝结流动的影响，导致相间滑移的主要因素为液滴在蒸汽中的黏性阻力。根据White等[6-7]实验数据，自发凝结产生的水滴平均半径在40～80 nm。水滴尺寸与气体平均自由程在同一数量级上，因此液滴在蒸汽中的黏性阻力不可忽略。单位体积湿蒸汽中液滴所受的黏性阻力计算式为

(6)

为Cunningham阻力修正系数，其主要与Knudsen数有关。其计算式为

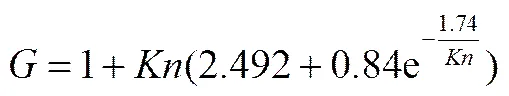
rp为液相弛豫时间，其主要与阻力系数相关。计算式为

(8)

连续性方程

双流体模型中的汽相动量守恒方程为

(10)

双流体模型中的液相动量守恒方程为

能量方程为

(12)

湿度计算式为[21-22]

两相湍流模型采用SST--d，与-模型相比，SST--d模型可较好地对附着流进行计算。采用能精确捕捉凝结流场流动特征的高分辨率二阶TVD格式进行离散[15-16]。

1.3 物理模型及实验工况

本文研究对象为某凝汽式汽轮机低压缸末级动叶顶部通道，该叶栅叶片间距为36.92 mm，叶片轴向弦长19.2 mm，叶型弦长为76 mm，叶栅汽流进口角为128°。叶栅进口和出口为压力边界条件，叶栅通道为周期性边界条件，叶片表面为固壁边界条件，叶栅几何形状见图3。

动叶顶部通道采用非结构化四边形网格，对叶片表面、尾缘、通道喉部网格进行加密处理。非结构化四边形网格对不规则的动叶顶部通道模型适应性较强，大部分网格的排列方向与流动方向相同，非结构化四边形网格的应用在一定程度上提高了数值模拟的收敛速度和计算精度。计算网格由ANSYS ICEM软件生成，为了排除网格因素给计算带来的误差，需进行网格无关性验证。选取了从1.2万个至9.6万个共4套拓扑结构相同的计算网格进行网格无关性验证，发现网格大于3.6万个时，叶片表面压力随网格的增加变化很小，由此可见3.6万个的网格规模已经可以满足网格无关性要求，因此本文计算网格确定为3.6万个。

根据2/0和出口Mach数情况，本文共设计了8种实验工况，其中跨声速流动工况2种，超声速流动工况6种，具体情况如表1所示。

表1 各实验工况参数

根据2/0可将本文实验工况分为4组，相同压比下根据进口过冷度不同，湿蒸汽凝结流动又可分为过热蒸汽流动工况和自发凝结流动工况。

2 数值模拟结果与分析

2.1 模型验证

为了验证本文数值模型的准确性，取文献[4]中的叶片表面压力实验数据，与本文计算结果进行对比，见图4。由图4可知，8种工况压力面的压比计算值与实验数据吻合得都很好，但吸力面后半段存在一定误差。

对于2/0=0.55跨声速流动，由图4(a)可知，工况1吸力面轴向弦长50%处存在燕尾形激波，数值计算很好地捕捉到了由于燕尾形激波引起的压力突跃，说明数值计算方法的精度较高。与工况2相比，工况1的压力突跃更为显著，说明过热蒸汽工况比凝结流动工况的压力突跃大。对于过热蒸汽工况，其压力突跃是由于蒸汽在吸力面膨胀后出现气动激波导致的；而对于凝结流动工况，其压力突跃除了气动激波外还受凝结激波影响。燕尾形激波与凝结激波的相互耦合后，导致凝结流动现象十分复杂，因此工况2计算结果没有能够很好地捕捉到气动激波与凝结激波耦合产生的压力突跃。

对于2/0=0.43的超声速流动，压力面的压比计算值与实验值吻合得很好，但吸力面后半段存在较大误差，这主要由于燕尾形激波的两个分支连续对吸力面气流干涉，增加了流动状况的复杂性。工况3为过热蒸汽流动，工况4～工况6为自发凝结流动。与工况1跨声速流动相比，工况3超声速流动存在两次压力突跃，第1次位于45%轴向弦长处，第2次位于65%轴向弦长处。第1次压力突跃是由于湿汽在吸力面膨胀后出现气动激波导致的，第2次压力突跃是由于相邻叶片尾缘处形成的燕尾形激波打到吸力面65%轴向弦长处导致的。工况4～工况6中的凝结现象会使吸力面边界层分离点前移，导致分离区增厚。对于进口过冷度较小的工况4和工况5，压力突跃位置及大小预测的较为准确；而对于进口过冷度较大的工况6，几乎无法捕捉到凝结激波导致的压力突跃。研究表明：吸力面50%～60%轴向弦长处的计算结果存在较大误差。该段处于湿蒸汽成核区，气流快速膨胀产生大量凝结核并释放凝结潜热，导致实验值和计算值出现误差。吸力面60%～90%轴向弦长处的压比计算值小于实验值，这主要由于凝结冲波和燕尾形激波相互干涉，增加了流动的复杂性，影响了叶片表面边界层状态，使得此处的凝结参数计算值出现误差。

对于2/0=0.28的超声速流动，压力面的压比计算值与实验值吻合得很好，但吸力面70%～90%轴向弦长处的压比计算值小于实验值，但总体吻合度比2/0=0.43的超声速流动好。与工况3相同，工况7的吸力面也存在两次压力突跃，第1次45%轴向弦长处，第2次位于70%轴向弦长处。工况7的两次压力突跃形成原因与工况3相同，但其压力突跃程度小于工况3。在工况7和工况 8 中，计算值均能准确预测压力突跃的位置和大小。

2.2 成核率分布

汽轮机叶栅通道中的湿蒸汽凝结流动既是热力不平衡过程，同时也是动力不平衡过程。湿蒸汽中的液相为多元弥散相，包含大量不同尺度的微小水滴，研究湿蒸汽成核率和水滴数的分布规律对湿汽损失控制具有重要意义。图5为工况2、工况4、工况5、工况6、工况8的成核率分布。

图5(a)为跨声速流动成核率分布，其主要发生在动叶栅喉部下游区域。成核率在吸力面30%轴向弦长和压力面尾缘附近达到最大，峰值为8.69×1025kg-1s-1。图5(b)为不同压比下超声速流动成核率分布，工况4、工况5、工况8的成核区域及成核率峰值位置与工况2类似，但工况6成核率分布与其他工况出现了明显差异。工况4、工况5、工况6的成核率峰值分别为5.68×1026、4.52×1026、1.26×1026kg-1s-1，3种工况的成核率峰值都在相同数量级，但随着过冷度的增加，成核区域面积逐渐增大。由于工况6的进口过冷度为-19.44 K，较大的过冷度导致蒸汽从叶栅入口就开始出现成核过程，成核率峰值位置也提前，这也是工况6几乎无法捕捉到压力突跃的原因。工况8的成核率峰值为5.64×1026kg-1s-1，与2/0=0.43的超声速流动工况在同一数量级上，只是其成核区域面积较小。

2.3 水滴数分布

图6为工况2、工况4、工况5、工况6、工况8的水滴数分布。由图6可以看出，叶栅尾迹中的水滴数明显高于主流区，这是由于成核现象首先出现在吸力面。成核现象伴随着大量水滴生成，随后吸力面分离产生的涡团向喉部下游移动，在尾缘处与尾迹涡混合，涡团掺混将吸力面附近的大量水滴带入尾迹。此外，压力面尾缘处的局部曲率很大，主汽流在此处迅速偏转并伴随剧烈膨胀，使得大量的凝结核随汽流进入尾迹。因此叶栅尾迹中水滴数明显高于通流部分，但是此处的水滴半径比主流区低1～2个数量级。随着大量微小水滴进入尾迹区，削弱了该区域内的热力不平衡性，导致过冷度减小。

2/0是影响水滴分布的主要因素。对于2/0=0.55跨声速流动，工况2尾迹处的水滴数峰值为1.16×1024m-3；对于2/0=0.43的超声速流动，工况4、工况5、工况6尾迹处的水滴数峰值为6.55×1022、8.63×1022、9.97×1022m-3；对于2/0=0.28的超声速流动，工况8尾迹处的水滴数峰值为2.59×1020m-3。由此可知，随着2/0的不断降低，叶栅尾迹中的水滴数逐渐减少，但主流区的水滴数逐渐增加。因此，水滴数并非完全受成核率影响，激波干涉和涡团掺混也会对水滴分布产生较大影响。

2.4 湿度分布

图7给出了非平衡凝结流动各工况的湿度分布。成核现象发生后，叶栅通道中湿度值迅速增大，在吸力面70%轴向弦长处达到一个峰值，随后湿度开始逐渐减小。这主要因为凝结流动受背压影响，经历一段加速过程后开始减速，导致当地温度和压力增加，部分液滴被蒸发。但随着水滴生长过程不断进行，水滴半径增加，湿度又开始增大。

各工况尾迹区的湿度均显著低于主流区。其原因在于尾迹区域的过冷度较小，此区域内的水滴生长速度缓慢，虽然该区域中的水滴数比主流区高2～4个数量级，但尾迹区的水滴半径较小，由式(13)可知，湿度与水滴半径的3次方呈正比，因此尾迹区的湿度比主流区小。对于2/0=0.55跨声速流动，工况2最大湿度为0.045；对于2/0=0.43的超声速流动，工况4、工况5、工况6最大湿度为0.484、0.558、0.617；对于2/0=0.28的超声速流动，工况8最大湿度为0.689，大于工况5，说明相同进口过冷度下，2/0越小，叶栅出口湿度越大。

3 结 论

研究湿蒸汽凝结流动问题对提高蒸汽轮机效率具有重要意义。本文在自发凝结理论的基础上，对经典均质成核理论进行推导和总结，得出了适用范围广的成核模型，采用考虑相间作用及湍流影响的双流体数值模型对湿蒸汽超声速凝结流动进行研究，重点讨论了叶片表面压力、成核率、水滴数、湿度的分布规律和影响因素，结论如下。

（1）各工况压力面的压比计算值与实验数据吻合得都很好，但吸力面后半段存在一定误差，这主要由于凝结冲波和燕尾形激波相互干涉，增加了流动的复杂性，影响了叶片表面边界层状态，使得此处模拟较为困难。

（2）本文模型对于过热工况和入口过冷度较小的凝结工况适应性较好，但对于入口过冷度较大的凝结工况，几乎无法捕捉到凝结激波导致的压力突跃。

（3）水滴数并非完全受成核率影响，激波干涉和涡团掺混也会对水滴分布产生较大影响，涡团掺混将吸力面附近的大量水滴带入尾迹，削弱了该区域内的热力不平衡性，导致局部过冷度减小，水滴生长速度缓慢，因此尾迹区的湿度小于主流区。

符 号 说 明

E——能量密度，kJ·m-3 FD——黏性阻力，N G——Cunningham阻力修正系数 hfg——凝结潜热，kJ·kg-1 ht——蒸汽总焓，kJ·kg-1 J——单位体积成核率, (m3·s)-1 Kn——Knudsen数 k——Boltzmann常数 m——单分子的质量，kg ——质量凝结速率，kg·s-1 N——单位体积蒸汽中的水滴数量, m-3 p——蒸汽实际压力，Pa Prg——Prandtl数 qc——凝结系数 R——气体常数 Red——水滴相对于气体运动的 Reynolds 数 r——水滴半径，m rc——临界水滴半径，m S——过饱和度 T——温度，K ΔT——过冷度，K u——轴向速度，m·s-1 v——径向速度，m·s-1 Y——湿度 a——分子聚团表面传热系数，W·(m2·K)-1 δ——水滴生长半经验修正系数 λg——蒸汽的热导率，W·(m·K)-1 μl——层流黏性系数 nd——液相层流黏性系数 nt——液相湍流黏性系数 ρ——密度，kg·m-3 ρd——液相的体积平均密度，kg·m-3 s——水滴表面张力，N·m-1 τrp——液相弛豫时间，s 下角标 g——气相参数 i——第i个水滴 l——液相参数

References

[1] MOORE M J. Two-Phase Steam Flow in Turbines and Separators[M]//SIEVERDING C H. Washington DC: Hemisphere Publishing Corporation, 1976: 5-6.

[2] MOORE M J. Aerothermodynamics of Low Pressure Steam Turbines and Condensers[M]// SIEVERDING C H. Washington DC: Hemisphere Publishing Corporation, 1987: 12-14.

[3] KHOMUTSKII A N, DEICH M E, SHCHERBAKOV A P,. Supersonic flow of wet steam around the trailing edges of cascades[J]. Teploenergetika, 1990, 37(8): 63-65.

[4] BAKHTAR F, MASHMOUSHY H, BUCHLEY J R. On the performance of a cascade of turbine rotor tip section blading in wet steam(Ⅰ): Generation of wet steam of prescribed droplet sizes[J]. Proc. Instn. Mech. Engrs. Part C, 1997, 211(8): 519-529.

[5] BAKHTAR F, MASHMOUSHY H, JADAYEL O C. On the performance of a cascade of turbine rotor tip section blading in wet steam(Ⅱ): Surface pressure distributions[J]. Proc. Instn. Mech. Engrs. Part C, 1997, 211(9): 531-540.

[6] WHITE A J. A comparison of modeling methods for polydispersed wet-steam flow[J]. Int. J. Numer. Meth. Eng., 2003, 57(57): 819-834.

[7] WHITE A J, HOUNSLOW M J. Modelling droplet size distributions in polydispersed wet-steam flows[J]. Int. J. Heat Mass Tran., 2000 , 43(11): 1873-1884.

[8] LI L, LI Y, WU L,. Numerical study on condensing flow in low pressure cylinder of a 300MW steam turbine[C]//ASME Turbo Expo 2010: Power for Land, Sea and Air. UK: American Society of Mechanical Engineers, 2010: 2289-2296.

[9] 李瑜, 李亮, 钟刚云, 等. 末级透平对低压缸气动和凝结特性的影响[J]. 西安交通大学学报, 2012, 46(7): 16-20. LI Y, LI L, ZHONG G Y,. Influence of last stage turbine on aerodynamic performance and condensation characteristic of low pressure cylinder[J]. Journal of Xi’an Jiaotong University, 2012, 46(7): 16-20.

[10] 巫志华, 李亮, 丰镇平. 三维湿蒸汽自发凝结流动的数值模拟[J]. 动力工程, 2006, 26 (6): 814-817. WU Z H, LI L, FENG Z P. Numerical simulation of 3D wet steam flow with spontaneous condensation[J]. Journal of Power Engineering, 2006, 26 (6): 814-817.

[11] 吴晓明, 李亮, 李国君, 等.基于双流体模型的湿蒸汽凝结流动三维数值模拟[J]. 热能动力工程, 2007, 22(4): 367-370. WU X M, LI L, LI G J,. Three-dimensional numerical simulation of wet steam condensation flows based on a dual fluid model[J]. Journal of Engineering for Thermal Energy & Power, 2007, 22(4): 367-370.

[12] WU X M , LI L, LI G J,. Numerical investigation of the effect of inlet condition on self-excited oscillation of wet steam flow in a supersonic turbine cascade[J]. Int. J. Numer. Meth. Fluids, 2009, 60(12): 1334-1350.

[13] 朱晓峰, 林智荣, 袁新. 透平级中湿蒸汽均/异质凝结流动的数值方法[J]. 清华大学学报(自然科学版), 2012, 52(7): 973-979. ZHU X F, LIN Z R, YUAN X. Homogeneous/ heterogeneous condensing flow modeling in turbine cascades[J]. Journal of Tsinghua University(Science and Technology), 2012, 52(7): 973-979.

[14] 林智荣, 袁新. 自发凝结流动数值模拟方法及其在Laval喷管中的应用[J]. 工程热物理学报, 2006, 27(1): 42-44. LIN Z R, YUAN X. A numerical method for spontaneous condensing flow and its application on Laval nozzle[J]. Journal of Engineering Thermophysics, 2006, 27(1): 42-44.

[15] 张冬阳, 蒋洪德, 刘建军. 考虑若干影响的一元蒸汽凝结流数值解[J]. 工程热物理学报, 2001, 22(s1): 25-28. ZHANG D Y, JIANG H D, LIU J J. Numerical calculation of one dimensional steam nucleating flow by considering some influences[J]. Journal of Engineering Thermophysics, 2001, 22(s1): 25-28.

[16] 张冬阳, 刘建军, 蒋洪德. 三维湿蒸汽流动快速准确数值模拟方法及应用[J]. 工程热物理学报, 2003, 24(2): 262-264. ZHANG D Y, LIU J J, JIANG H D. The approach and application of fast and accurate numerical simulation on 3d wet steam flow[J]. Journal of Engineering Thermophysics, 2003, 24(2): 262-264.

[17] 鞠凤鸣, 王祥锋, 颜培刚, 等. 末级中空静叶除湿方法的数值研究[J]. 汽轮机技术, 2011, (5): 331-334+388. JU F M, WANG X F, YAN P G,. Numerical simulation on moisture removal method of final stage hollow vane[J]. Turbine Technology, 2011, (5): 331-334.

[18] 鞠凤鸣, 颜培刚, 陈晓娜, 等. 除湿槽对涡轮叶栅非平衡凝结流动的影响[J]. 哈尔滨工业大学学报, 2013, 45(9): 35-41. JU F M, YAN P G, CHEN X N,. Influence of moisture removal slot on wet steam non-equilibrium condensation flow in turbine cascade[J]. Journal of Harbin Institute of Technology, 2013, 45(9): 35-41.

[19] 韩中合, 陈柏旺, 刘刚, 等. 湿蒸汽两相凝结流动中水滴生长模型的研究[J]. 中国电机工程学报, 2011, 31(29): 79-84. HAN Z H, CHEN B W, LIU G,. Droplets growth model in wet steam two-phase condensation flow [J]. Proceedings of the CSEE, 2011, 31(29): 79-84.

[20] HAN Z H, HAN X, LI H F,. Comparative study of homogeneous nucleation rate models for wet steam condensing flows[J]. Korean J. Chem. Eng., 2016, 33(12): 3487-3492.

[21] 韩中合, 韩旭, 李恒凡. 叶栅通道内湿蒸汽非平衡凝结流动的数值模拟[J]. 化工学报, 2016, 67(5): 1806-1813. HAN Z H, HAN X, LI H F. Numerical simulation of wet steam non-equilibrium condensing flow in cascade passage[J]. CIESC Journal, 2016, 67(5): 1806-1813.

[22] 韩中合, 韩旭, 李鹏. 湿蒸汽非平衡凝结流动的热力学特性[J]. 化工学报, 2015, 66(11): 4312-4319. HAN Z H, HAN X, LI P. Effect of thermodynamic properties on wet steam non-equilibrium condensing flow [J]. CIESC Journal, 2015, 66(11): 4312-4319.

[23] 钱江波, 韩中合, 张美凤, 等. 蒸汽参数突变对蒸汽湿度测量的影响分析[J]. 工程热物理学报, 2013, 34(5): 888-891. QIAN J B, HAN Z H, ZHANG M F,. Analysis of steam parameters mutations affecting to measure steam wetness[J]. Journal of Engineering Thermophysics, 2013, 34(5): 888-891.

[24] HAN Z H, HAN X, WANG Z. Numeric simulation of wet-steam two-phase condensing flow in a steam turbine cascade[J]. J. Braz. Soc. Mech. Sci., 2017, 39(4): 1189-1199.

[25] WÖLK J, STREY R, HEATH C H,. Empirical function for homogeneous water nucleation rates[J]. J. Chem. Phys., 2002, 117(10): 4954-4960.

[26] ANDERSON R J, MILLER R C, KASSNER J L,. A study of homogeneous condensation freezing nucleation of small water droplets in an expansion cloud chamber[J]. J. Atmos, 1980, 37: 2509-2520.

[27] MILLER R C, ANDERSON R J, KASSNER J L. Homogeneous nucleation rate measurements for water over a wide range of temperature and nucleation rate[J]. J. Chem. Phys., 1983, 78(6): 3204-3211.

[28] WHITE A J, YOUNG J B, WALTERS P T. Experimental validation of condensing flow theory for a stationary cascade of steam turbine blades[J]. Philos. Trans. R. Soc. Lond. , 1996, 354(1704): 59-88.

Supersonic condensation flow characteristics of wet steams in turbine rotor blade tip section

HAN Xu, HAN Zhonghe

(Key Laboratory of Condition Monitoring and Control for Power Plant Equipment, North China Electric Power University, Ministry of Education, Baoding 071003, Hebei, China)

Steam turbines are critical power generation equipment in electric power industry. Understanding water vapor condensation flow is important to improve efficiency and safety of steam turbines. Due to complexity of high speed condensation flow in steam turbines, no universally accepted nucleation model is available at present and current numerical models usually neglect vapor-liquid slip. Considered steep distribution and change sensitivity of condensing parameters, a double fluid numerical model of shear stress transport (SST)--dtwo-phase turbulence,which can not only describe transonic flow of compressible gas accurately but also capture parameter jump instantly, was used to analyze condensation flow characteristics in turbine rotor blade tip section.The study revealed influence of pressure ratio on non-equilibrium condensation flow characteristics of wet steams and summarized changing patterns of surface pressure, nucleation rate, humidity, and number of water droplets.Results showed that calculation of pressure ratio at compression surface was in good agreement with experimental data under various operating conditions, although some error was observed in the second half of suction surface. The two fluid numerical model was applicable to both overheating operation and condensations with slight overcooling inlet. But pressure jump caused by condensation shock could hardly be caught for large overcooling inlet. Shock wave interference and vortex mixing had a great influence on distribution of water droplets.

wet steam; steam turbine;supersonic; two-phase flow; condensation; thermodynamics

10.11949/j.issn.0438-1157.20170678

O 354

A

0438—1157（2017）09—3388—09

2017-05-25收到初稿，2017-06-26收到修改稿。

韩中合。

韩旭(1991—)，男，博士研究生。

国家科技支撑计划项目(2014BAA06B01);中央高校基本科研业务费专项资金项目(2016XS106)。

2017-05-25.

HAN Zhonghe, han_zhonghe@163.com

supported by the National Science and Technology Support Program (2014BAA06B01) and the Fundamental Research Funds for the Central Universities(2016XS106).