基于密度泛函理论的活性炭孔径分布改进算法
朱子文,郑青榕,陈武,王泽浩,唐政
基于密度泛函理论的活性炭孔径分布改进算法
朱子文,郑青榕,陈武,王泽浩,唐政
(福建省船舶与海洋工程重点实验室,集美大学轮机工程学院,福建厦门 361021)
为提高非定域密度泛函理论(NLDFT)预测活性炭孔径分布(PSD)的精度,考虑了活性炭孔壁面晶体粗糙度对结果的影响。在传统NLDFT基础上,结合吸附壁面碳原子的密度分布,推导出改进NLDFT,预测了氩在光滑及具粗糙碳晶体表面的吸附平衡,并根据87.3 K、氩在活性炭上的吸附平衡数据,在由两种NLDFT确定了不同孔径的理论等温线核后,由寻优函数确定活性炭在0.35~12 nm区间的PSD。结果表明,以改进的NLDFT预测活性炭的PSD时,确定的活性炭孔径呈连续分布,预测平衡数据的相对误差小于10%;传统NLDFT确定的孔径在1 nm处出现断点,最大的预测相对误差范围达45%。改进NLDFT能较准确预测氩在具有粗糙晶体碳表面活性炭的PSD。
氩;活性炭;吸附;分布;密度泛函理论
引 言
由于活性炭具有较大的微孔容积和比表面积,其在物理吸附储氢、吸附式天然气存储(ANG)以及二氧化碳的吸附捕集等领域具有光明的应用前景[1]。然而,由于吸附质分子直径及极性的差异,适合于不同吸附质分子吸附的活性炭具有不同的孔径分布(PSD),如何准确获取用于描述吸附平衡的活性炭PSD极为关键。
当前,表征活性炭PSD的方法主要有BJH、t-plot、H-K、DR理论和非定域密度泛函理论(NLDFT),NLDFT具有较高的预测精度[2-3]。吸附过程中,近吸附剂壁面的吸附质分子受吸附势作用,密度分布出现振荡。在早期的研究中,Tarazona等[4-5]提出了光滑密度近似(SDA)的概念,Lastoskie等[6]将SDA应用于确定活性炭的PSD,Neimark[7]则引入不定Lagrange因子法(ILM)简化求解过程,而Ustinov等[8]在求解过程时进一步考虑了一维能量分布不均匀项(EH)。随后2D-NLDFT[9]、基于基本度量理论(FMT)[10-11]及统计缔合流体理论(SAFT)[12-13]的NLDFT模型被逐渐应用。然而,由上述方式确定的流体在第一层内的局部密度过于密集,偏离了假设的硬球模型,PSD计算结果在1 nm处出现不连续的情况[14]。为此,Ustinov将非石墨化碳黑以及活性炭狭缝孔视为能量分布非均匀表面,通过对实验数据进行非线性拟合确定了表面碳原子密度分布误差函数,并将具有粗糙碳晶体表面近似为吸附质的淬火状态(quenched),而靠近壁面区域的流体分子则近似为退火状态(annealed),通过改进Carnahan-Starling(CS)方程求解混合状态过剩自由能,最终由吸附数据拟合确定碳原子表面对流体分子施加的作用势[15-19]。Ravikovitch等[20]则将具有粗糙碳晶体表面视为淬火相态的碳原子,提出了骤冷固体密度函数理论(QSDFT),利用FMT求解该二元硬球流体排斥项,预测了氮、氩在硅胶上的吸脱附平衡,并通过X射线衍射仪(XRD)衍射结果确定表面碳原子密度分布后,计算了活性炭的PSD[21-22]。郑青榕等[23-24]引入碳原子表面密度分布误差函数,结合氢在活性炭以及石墨化碳黑上的吸附数据,确定了活性炭的PSD。上述文献引入碳原子表面密度分布的误差函数后,均保证了在1nm处PSD的连续性,提高了计算精度。而对于处于亚临界区域的吸附质,在压力变化较大的区间,吸附相为液相或过冷液态,粗糙的吸附壁面使流体出现毛细凝聚和起泡等现象。为准确描述上述现象,改进FMT以及SAFT等理论被拓展应用于确定受限流体密度分布,但相关理论的泛函方程求解过程复杂[12-13,25]。
基于此,为精确预测活性炭的PSD,基于传统NLDFT,参考Ustinov以及Ravikovitch等考虑活性炭孔壁面粗糙度对于预测PSD的研究,通过引入表面碳原子密度分布函数改进NLDFT,预测氩在具有光滑与粗糙晶体表面的碳黑上的吸附平衡后,依据氩在活性炭SAC-01上吸附平衡数据,比较了两种NLDFT确定的活性炭PSD。
1 试 验
活性炭(SAC-01)试样由福建宁德鑫森碳业有限公司提供。为确定SAC-01活性炭的PSD,本文选用Micromeritics 3Flex固体表面分析仪于液氩温度下测得吸脱附等温线,结果如图1。更多实验信息参阅文献[26]。
从图1看出,氩在SAC-01活性炭上的吸脱附等温线在/0>0.4区域具有“滞回”现象,表明SAC-01活性炭具有介孔和大孔。通过BET法以及脱附数据利用BJH法确定的结构参数如表1所示。

表1 SAC-01活性炭结构参数
2 基本理论
2.1 传统理论
在给定化学势和温度的条件下,自由能是决定系统平衡特性最重要的热力参数。对于非均质系统,一维分布的受限流体的自由能可表示为[8]

式中,()为流体沿壁面处垂直方向的密度分布曲线。吸附平衡时,吸附自由能为最小值,密度分布曲线满足。
本征自由能[()]由理想气体自由能id和流体分子的过剩自由能ex构成。id可由式(2)求得

其中,B为Boltzmann常数,为de-Broglie波长。而ex可区分为流体分子间吸引项att和根据硬球分子间排斥力HS[()]。根据平均场理论,流体分子间吸引项为[27]
(3)
其中,()与(′)为位于三维空间内与′局部位置的密度分布,对于一维模型,局部密度分布函数只与垂直壁面方向相关;相吸自由能att由WCA扰动理论近似[28]。

(5)

(7)
式中,w为加权系数,=0,1,2。对于一维平均密度求解过程可参阅文献[9]。
传统NLDFT理论认为碳材料表面可视为光滑壁面。壁面对于流体分子施加的作用势ext可由10-4-3势能方程确定

式(8)相关参数如表2,物理意义参阅文献[29]。

表2 氩在碳表面上吸附的物性参数[15]
化学势可由CS状态方程求得[8]

其中,g为本体气相密度,则;末项为由WCA扰动理论计算的本体气相流体分子间相互作用,。
联立式(1)~式(9)可得受限流体的自由能方程;基于平衡条件,即可对相应的巨势[()]取最小值而获得密度分布()。本文利用ILM法求解[()]最小值,详细过程参见文献[7]。
2.2 改进NLDFT
Ustinov等[15]认为活性炭孔墙为表面能量不均匀且为粗糙晶体的碳原子表面,并将其近似为非石墨化碳黑表面。对于非石墨化碳黑BP280,可附加关于壁面碳原子表面的密度分布误差函数

其中,为碳原子表面分布修正系数,与Ustinov不同,本文依据Ravikovitch等对于BP280的XRD衍射结果,取0.026nm[16]。对于近壁面的硬球流体,受到的壁面作用势呈现不均匀分布,该区域流体密度分布需要引入附加项加以修正
(11)
其中,e()为等效密度分布;在靠近壁面区域,可将壁面视为粗糙晶体的碳表面,吸附质分子与表面碳原子晶体呈相互作用的混合状态,由于该区域表面碳原子的密度大于吸附质分子密度却远小于石墨层内碳原子密度,故可将表面碳原子密度等效为吸附质的淬火相态密度m,。同样利用SDA求解其光滑密度,则吸附壁面对流体施加的排斥项为[16]

与Ustinov等利用最小二乘法拟合确定壁面对于流体分子施加的作用势不同,本文利用WCA扰动理论确定碳原子与流体分子间的相吸自由能[16]
(13)
考虑吸引与排斥项的共同作用,通过积分求得流体受到壁面施加的作用势ext

其中,s为碳黑石墨层内碳原子密度。
由式(1)~式(13)确定粗糙晶体碳表面吸附平衡时的自由能,并对相应的巨势[()]取最小值即可得到密度分布()。将传统NLDFT求解的密度分布设为初值,再由数值迭代求解粗糙表面的密度分布()。在此,针对一维分布的受限空间,以Δ0.005ff构建空间内相应位置分布的矩阵,通过Picard迭代利用Matlab的矩阵运算离散求解[25]。
3 吸附平衡分析
3.1 氩在碳黑上的吸附平衡
根据文献[30],87.3 K时,氩在石墨化碳黑CarbopackF(BET=6.2 m2·g-1)以及非石墨化碳黑BP280(BET=36 m2·g-1)上的吸附数据如图2所示[图2(b)为对数坐标]。在此,石墨化碳黑CarbopackF近似为表面光滑的碳表面,而非石墨化碳黑BP280则具有粗糙晶体碳表面。利用传统NLDFT及改进NLDFT的预测结果如图2所示,氩在不同碳表面上的密度分布的计算结果如图3所示。
由图2(a)可发现,传统NLDFT的预测结果与氩在石墨化碳黑CarbopackF上吸附等温线较为接近,而改进NLDFT的预测结果则与氩在BP280上的吸附等温线更为吻合。从图2(b)还可发现,在低压区域,改进NLDFT的预测结果与CarbopackF的吸附数据间差距较大;在/0=0.01~0.1范围内,改进NLDFT预测值与氩在BP280吸附数据有显著误差,但在其他区域具有较高的预测精度。如图2(b)所示,/0=0.1时氩在碳黑表面上为单层吸附且接近最大值,图2中改进NLDFT预测值小于实验值,这说明仅引入一维误差函数,仍无法准确描述碳黑表面的晶体分布,需进一步建立二维模型[9]。
由图3更为直观地发现两者的区别:坐标原点为第1层碳原子的中心位置,由传统NLDFT确定密度分布起始点距壁面约0.5ff,而改进NLDFT的密度分布变化则从壁面开始。这表明在粗糙晶体的碳表面,由于表面能量分布不均匀,氩将优先聚集在吸附作用势较强的吸附位上。此外,传统NLDFT确定的氩在碳黑表面的密度分布函数()明显比改进NLDFT确定的振荡幅度大,如第1层流体分子的局部密度最大值()3ff=7,而改进NLDFT确定的密度分布则较为平缓,其值在液氩(L3ff=0.76[15])相态附近。显然,改进的NLDFT更适合于描述氩在具有粗糙晶体表面碳基材料上的吸附平衡。
3.2 PSD的寻优确定
活性炭吸附空间可视为两侧由无限大碳黑平板构成的狭缝孔,其孔径为两侧壁面间的距离[3]。在实际求解壁面对流体分子的作用势时,计算距离为对应壁面碳原子间的中心距离*,其中*=+[31]。为石墨层厚度,=0.34 nm。
狭缝孔内的流体分子受到的壁面作用势为[26]

(16)
求解过程中由于需要对密度分布函数作离散化处理,首先由梯形数值积分求得流体在不同孔径的理论吸附等温线核(,)[23]

其中,(,)是与平衡压力和孔宽对应的吸附量。传统NLDFT求解的、孔径为0.35~12 nm的等温线核()如图4(a)所示,图中的压力与图1中测试点的平衡压力对应。由改进NLDFT计算结果如图4(b)所示。
对比图4(a)和图4(b)可发现,改进NLDFT求解的等温线随压力的变化较为平缓;孔径较小、相对压力/0>0.01时,氩的吸附相密度将逐渐增大并超过液氩密度;孔径增大时,不同孔内吸附相发生相变的临界压力也随之增大,尤其在介孔范围,当/0>0.4时,吸附相密度呈直线急剧上升。
积分吸附等温方程(IAE)为

其中,max=12 nm;()为孔径分布函数。根据之前的研究,需要考虑氩在大于max的狭缝孔内的吸附量[23-24]
(19)
式中,为图1等温吸附线中吸附平衡压力的点数,本文=77;附加项ext为氩在大于max的狭缝孔内的吸附量,可由图2中氩在碳黑CarbopackF/BP280上吸附面密度插值计算获得,ext为类似碳黑的外表面积。由此可以构建一个关于不同孔的理论吸附等温线核(,)的×(-1)矩阵,将式(19)附加项加入该矩阵,变为维矩阵|(,)|。同样地,增量体积Δv与外面积ext也可组成一个长度为的向量|Δ|,式(19)可变为=的矩阵运算。由于增量体积|Δ|为非负向量,直接求解该线性方程无法得到具有物理意义的解。
因此,需要确定关于增量体积|Δ|向量的寻优函数以进行数值求解,设误差函数为,且满足约束条件|err|<0.1,则寻优函数为
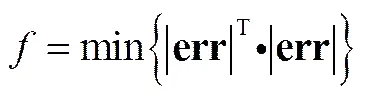
利用MATLAB中Optimtool工具箱中函数fmincon求出最优解|Δ|,两种NLDFT预测的吸附等温线如图5所示。
图5 87.3 K氩在活性炭SAC-01上的吸附等温线测试值与预测值
Fig.5 Isotherms of argon adsorption on activated carbon SAC-01 at 87.3 K from experiments and calculations
由两种NLDFT的预测值与实验数据间的相对误差|err|/exc×100%如图6所示。
如图6所示,由改进NLDFT预测值与实验数据间的相对误差范围在±10%,当/0>10-5时,相对误差约在±1%,而传统NLDFT的相对误差范围在-20%~45%。这说明,将活性炭狭缝孔墙视为粗糙的碳原子表面,并由改进NLDFT预测其孔径分布更为合理。
孔径分布函数()与增量体积Δv的关系为[31]

其中,Δ为该孔孔径的增量;ΔNLDFT为孔内增量面积。利用式(21)即可求出活性炭的孔径分布PSD如图7所示,累积孔容与比表面积如表3所示。
图7 由不同算法确定的活性炭SAC-01的PSD
Fig 7 PSD of activated carbon SAC-01 determined by different approaches

表3 由PSD确定的SAC-01活性炭结构参数
从表3可看出,改进NLDFT的结果较为接近BET法确定的比表面积。从图7也可看出,两种方法的预测结果的变化趋势相似,即具有较大的微孔孔容,介孔变化趋势一致,但对于孔宽小于1 nm微孔的预测差异明显,传统NLDFT预测时,在1 nm处()为0,而改进的NLDFT则是连续的。这表明将活性炭孔墙视为具有粗糙晶体的碳表面是合理的。
4 结 论
根据活性炭具有表面能量分布不均匀的特点,附加碳原子粗糙表面密度分布改进传统NLDFT,对比了两种NLDFT对于氩在不同碳黑表面上的吸附行为的预测结果,得到如下结论。
(1)改进的NLDFT可更准确描述氩在具有粗糙晶体表面碳基材料上的吸附平衡。由传统NLDFT确定的氩在碳黑表面上的密度分布函数()振荡幅度大,如第1层流体分子的局部密度最大值()3ff7,而改进NLDFT确定的密度分布则较为平缓,其值在液氩相态附近波动。这说明由于在粗糙晶体的碳表面上,氩将优先聚集在吸附作用势较强的吸附位上,呈现不均匀分布。
(2)改进NLDFT在预测活性炭的PSD时具有较高的精度。利用改进NLDFT确定的活性炭孔径呈现连续分布,预测值与实验数据相对误差分布范围在±10%,传统NLDFT确定的活性炭孔径分布在1 nm处出现断点,相对误差分布范围在-20%~45%,说明将活性炭狭缝孔孔墙视为表面能量分布非均匀、碳表面粗糙的碳黑平板更为合理。
基于SDA理论的CS状态方程预测二元混合硬球流体的精度有待提高,后续研究需要考虑建立二维模型或利用FMT以及SAFT等理论进一步提高改进NLDFT对于活性炭PSD的预测精度。
符 号 说 明

dHS——硬球分子直径,nm F,Fid,Fex——分别为本征Helmholtz自由能、理想气体自由能和来自流体分子的过剩自由能,J fex——体系内吸附质分子的过剩自由能,J H,H*——狭缝孔两侧壁面间的距离及壁面碳原子间中心距离,nm kB——Boltzmann常数,J·K-1 N——吸附量,mmol·g-1 r,r′——分别为流体分子位于三维空间内r与r′的位置,nm S——比表面积,m2·g-1 u——流体分子间相互作用势,J V——壁面对流体分子施加的作用势,J v,Δv——比孔容积以及容积增量,cm3·g-1 z——流体分子与壁面碳原子中心的距离,nm Γ——吸附质的表面密度,mmol·m-2 Δ——碳原子层间距,nm δ——碳原子表面密度分布参数,nm ε——势阱,J ——堆积因子 μ——化学势,J r,——吸附质密度分布及光滑密度,nm-3 σ——分子直径,nm Ω——巨势,J 上角标 AC——活性炭 rep——排斥项 下角标 att——吸引项 BET——比表面积 e——等效 ex——过剩 ext——外部附加 ff——流体分子间 i——序号 m——淬火相态 max——最大值 mic——微孔 min——最小值 s——固体壁面 sf——流体相对于固体壁面
References
[1] POLICICCHIO A, FILOSA R, ABATE S,. Activated carbon and metal organic framework as adsorbent for low-pressure methane storage applications: an overview[J]. Journal of Porous Materials, 2016, 23(6): 1-18.
[2] 杨侃, 陆现彩, 徐金覃, 等. 气体吸附等温线法表征页岩孔隙结构的模型适用性初探[J]. 煤炭学报, 2013, 38(5): 817-821. YANG K, LU X C, XU J T,. Preliminary verification of common calculation methods of pore size distribution of shale based on gas adsorption isotherm[J]. JCSE Journal, 2013, 38(5): 817-821.
[3] LANDERS J, GOR G Y, NEIMARK A V. Density functional theory methods for characterization of porous materials[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2013, 437(6): 3-32.
[4] TARAZONA P. Free energy density functional theory for hard spheres[J]. Physical Review A, 1985, 31(4): 2672-2679.
[5] TARAZONA P, MARINI U, EVANS R. Phase equilibria of fluid interfaces and confined fluids[J]. Molecular Physics, 1987, 60(3): 573-595.
[6] LASTOSKIE C, GUBBINS K E, QUIRKE N. Pore size distribution analysis of microporous carbons: a density functional theory approach[J]. Journal of Physical Chemistry, 1993, 97(18): 1012-1016.
[7] NEIMARK A V. The method of indeterminate Lagrange multipliers in nonlocal density functional theory[J]. Langmuir, 1995, 11(10): 4183-4184.
[8] USTINOV E A, DO D D. Application of density functional theory to analysis of energetic heterogeneity and pore size distribution of activated carbons[J]. Langmuir, 2004, 20(9): 3791-3797.
[9] JAGIELLO J, OLIVIER J P. 2D-NLDFT adsorption models for carbon slit-shaped pores with surface energetical heterogeneity and geometrical corrugation[J]. Carbon, 2013, 55(2): 70-80.
[10] ZENG M, TANG Y, MI J,. Improved direct correlation function for density functional theory analysis of pore size distributions[J]. Journal of Physical Chemistry C, 2009, 113(40): 17428-17436.
[11] BALZER C, CIMINO R T, GOR G Y,. Deformation of microporous carbons during N2, Ar, and CO2adsorption: insight from the density functional theory[J]. Langmuir, 2016, 32 (32): 8265-8274.
[12] SCHINDLER B J, MITCHELL L A, MCCABE C,. Adsorption of chain molecules in slit-shaped pores: development of a SAFT-FMT-DFT approach[J]. Journal of Physical Chemistry C, 2013, 117(41): 21337-21350.
[13] MALHEIRO C, MENDIBOURE B, PLANTIER F,. Density functional theory for the description of spherical non-associating monomers in confined media using the SAFT-VR equation of state and weighted density approximations[J]. Journal of Chemical Physics, 2014, 140(13): 108-112.
[14] USTINOV E A. Comparative features of Ar adsorption on smooth and amorphous surfaces examined by density functional theory[J]. Adsorption, 2008, 14(2): 171-179.
[15] USTINOV E A, DO D D, FENELONOV V B. Pore size distribution analysis of activated Carbopacks: application of density functional theory using nongraphitized Carbopack black as a reference system[J]. Carbon, 2006, 44(4): 653-663.
[16] USTINOV E A, DO D D. Modeling of adsorption in finite cylindrical pores by means of density functional theory[J]. Adsorption, 2005, 11(5): 455-477.
[17] USTINOV E A, DO D D, JARONIEC M. Application of density functional theory to equilibrium adsorption of argon and nitrogen on amorphous silica surface[J]. Applied Surface Science, 2005, 252(3): 548-561.
[18] USTINOV E A, DO D D, JARONIEC M. Adsorption of argon and nitrogen in cylindrical pores of MCM-41 materials: application of density functional theory[J]. Applied Surface Science, 2005, 252(4): 1013-1028.
[19] USTINOV E A, DO D D, JARONIEC M. Equilibrium adsorption in cylindrical mesopores: a modified Broekhoff and de Boer theorydensity functional theory[J]. Journal of Physical Chemistry B, 2005, 109(5): 1947-1958.
[20] RAVIKOVITCH P I, NEIMARK A V. Density functional theory model of adsorption on amorphous and microporous silica materials[J]. Langmuir, 2006, 22(26): 11171-11179.
[21] NEIMARK A V, LIN Y, RAVIKOVITCH P I,. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons[J]. Carbon, 2009, 47(7): 1617-1628.
[22] GOR G Y, THOMMES M, CYCHOSZ K A,. Quenched solid density functional theory method for characterization of mesoporous carbons by nitrogen adsorption[J]. Carbon, 2012, 50(4): 1583-1590.
[23] 郑青榕, 蔡振雄, 陈武, 等. 非局域密度泛函理论表征活性炭孔径分布的改进算法[J]. 低温与超导, 2010, 38(1): 80-84. ZHENG Q R, CAI Z X, CHEN W,. An improved method to determine PSD of activated carbon by using non-local density functional theory [J]. Cryogenics and Superconductivity, 2010, 38(1): 80-84.
[24] 郑青榕, DO D D, 陈武, 等. 应用超临界温度氢吸附数据表征活性炭结构[J]. 离子交换与吸附, 2010, 26(6): 551-558. ZHENG Q R, DO D D, CHEN W,. Determination of the pore size distribution of the activated carbon by adsorption data of supercritical hydrogen [J]. Ion Exchange and Adsorption, 2010, 26(6): 551-558.
[25] ROTH R. Fundamental measure theory for hard-sphere mixtures: a review[J]. Journal of Physics Condensed Matter, 2010, 22(6): 503-511.
[26] 朱子文, 冯玉龙, 郑青榕. 甲烷在石墨烯和活性炭上的吸附[J]. 化工学报, 2015, 66(S2): 244-249. ZHU Z W, FENG Y L, ZHENG Q R. Methane adsorption on graphene sheets and activated carbon[J]. CIESC Journal, 2015, 66(S2): 244-249.
[27] BALL P C, EVANS R. Structure and adsorption at gas-solid interfaces: layering transitions from a continuum theory[J]. Journal of Chemical Physics, 1988, 89(7): 4412-4423.
[28] WEEKS J D, CHANDLER D, ANDERSEN H C. Role of repulsive forces in determining the equilibrium structure of simple liquids[J]. Journal of Chemical Physics, 1971, 54(12): 5237-5247.
[29] DO D D, DO H D, TRAN K N. Analysis of adsorption of gases and vapors on nonporous graphitized thermal carbon black[J]. Carbon, 2003, 19(14): 5656-5668.
[30] GARDNER L, MICHAL K A, JARONIEC M. Reference data for argon adsorption on graphitized and nongraphitized carbon blacks[J]. Journal of Physical Chemistry B, 2001, 105(50): 12516-12523.
[31] BIRKETT G, DO D D. New method to determine PSD using supercritical adsorption: applied to methane adsorption in activated carbon[J]. Langmuir, 2006, 22(18): 7622-7630.
Modified approach of determining pore size distribution of activated carbon by using density functional theory
ZHU Ziwen, ZHENG Qingrong, CHEN Wu, WANG Zehao, TANG Zheng
(Provincial Key Laboratory of Naval Architecture & Ocean Engineering, Institute of Marine Engineering, Jimei University, Xiamen 361021, Fujian, China)
In observation of accurately determining the pore size distribution (PSD) of activated carbons by employing thenon-local density functional theory (NLDFT), the effect of surface roughness resulted from the distribution of carbon atoms on the accuracy was evaluated in terms of comparison of the adsorption equilibrium of argon. The classical NLDFT, which was developed based on the approximation to the smooth distribution of the density near the surface, was modified by taking into account the influence from the uneven distribution of the carbon atoms on the surface. The accuracies of the results from the modified model were firstly evaluated by the adsorption data of argon on adsorbent surfaces which respectively have even and uneven distribution of carbon atoms. Experimental data of argon adsorption on the activated carbon at 87.3 K was then taken as a reference, and comparisons were accordingly made between the adsorption isotherms calculated by the classical and modified NLDFT. The PSD, which covers the range of 0.35—12 nm, was finally determined by employing optimization function. Results show that the modified model can bring about the continuous distribution of PSD, and the relative error between the results determined by calculationthe PSD and those from experiment can be less than 10%. However, the calculation from the classical model has an interrupt at a pore width about 1nm, and the resulted maximum relative error amounts to 45%. It suggests that the modified model can more accurately calculate the PSD of the activated carbon having uneven distribution of carbon atoms around the surface.
argon; activated carbon; adsorption; distributions; DFT
10.11949/j.issn.0438-1157.20170013
O 647.3; TQ 424.1
A
0438—1157(2017)09—3328—08
2017-01-06收到初稿,2017-06-12收到修改稿。
郑青榕。
朱子文(1991—),男,博士研究生。
国家自然科学基金项目(51679107);福建省自然科学基金项目(2015J01216)。
2017-01-06.
Prof.ZHENG Qingrong, qrzheng816@sina.com
supported by the National Natural Science Foundation of China (51679107) and the Department of Sciences & Technology of Fujian Province(2015J01216).

