结合高光谱信息的土壤有机碳密度地统计模型

刘艳芳，宋玉玲，郭 龙，陈奕云，卢延年，刘 以



结合高光谱信息的土壤有机碳密度地统计模型

刘艳芳1,2,3，宋玉玲1,2,3，郭 龙4，陈奕云1,2,5,6※，卢延年1,2,3，刘 以1,2,3

（1. 武汉大学资源与环境科学学院，武汉 430079； 2. 武汉大学地理信息系统教育部重点实验室，武汉 430079； 3. 数字制图与国土信息应用工程国家测绘地理信息局重点实验室，武汉 430079； 4. 华中农业大学资源与环境学院，武汉 430070； 5. 地球空间信息技术协同创新中心，武汉大学，武汉 430079； 6. 武汉大学苏州研究院，苏州 215123）

传统线性回归模型在借助光谱信息进行土壤属性预测时，通常忽略了土壤自身所具有的空间异质性和依赖性，并且未考虑模型残差的空间结构。针对以上不足，该文以江汉平原232个土壤样本为研究对象，以土壤反射光谱为辅助变量，采用偏最小二乘回归、普通克里格、协同克里格以及回归克里格分别构建土壤有机碳密度预测模型，选取决定系数（2）、均方根误差、标准差与预测均方根误差比（ratio of performance to deviation，RPD）对模型预测精度进行对比评价。结果显示，结合高光谱信息，且同时考虑残差空间结构的回归克里格模型表现优于其他模型，预测决定系数R为0.617，RPD为1.614。鉴于土壤光谱信息同时还具有测定简单、省时、无损等优点，因此土壤光谱是土壤有机碳密度空间插值的理想辅助因子。

土壤；模型；光谱分析；土壤有机碳密度；偏最小二乘回归；协同克里格；回归克里格

0 引 言

土壤是地球陆地表层最为活跃的碳库之一，是陆地生态系统的重要组成。农田土壤碳库关系到国家粮食安全和生态农业可持续发展[1]，农田土壤碳储量的变化及时空分异规律研究是当前地理信息科学、土地资源管理等学科的研究热点。其中，土壤有机碳密度（soil organic carbon density，SOCD）是土壤碳储量估算的重要参数，其时空信息的快速、高效获取是未来地理国情监测和国土资源调查的重要发展方向。然而，土壤本身是一个开放的复杂系统，由于受复杂的成土过程、自然环境要素以及人类活动等因素的影响，在不同的地区SOCD存在各具特点的空间分异规律，环境要素与SOCD的关系表现出一定的空间异质性，因此，考虑模型残差的空间结构特征对SOCD进行快速有效的预测具有积极的研究意义。

目前的研究主要采用野外采土样结合实验室化学分析的方法对SOCD进行测定，该方法操作耗时，步骤繁琐，与现代农业精准监测、全面管理的需求不匹配。但可见—近红外光谱测定分析能够达到便捷准确、节约成本、精确度高的要求，逐渐成为土壤组分估算预测的新方法[2]。土壤有机质中包含大量的氢基团，而近红外光谱可以很好地捕捉到有机质中含氢基团的变化，并根据光谱反射率的不同反推出含氢基团的数量特征，从而得到土壤有机质含量，最后将有机质含量和Bemmelen换算系数相乘[3]，得到土壤有机碳含量值，因此近红外光谱在技术上为快速测定SOCD提供了可行性[4]。近年来基于光谱信息的土壤属性的预测模型引起土壤和生态学者的关注[5]，由于其迅速、精确、无污染、不破坏样本等诸多的优点在土壤领域得到迅速的发展。然而现有研究通常视土壤样本为化学样本，进而采用传统线性回归模型，如偏最小二乘回归（partial least squares regression，PLSR）结合光谱信息进行土壤属性的拟合和预测。例如，李耀翔等采用近红外光谱技术对森林土壤有机碳含量进行研究[6-7]，表明结合光谱反射率能够对土壤有机碳含量进行有效测算，但是仅采用PLSR模型进行估算，忽略了土壤属性本身所具有的空间异质性。实际上土壤属性的空间特征在进行土壤属性预测及制图中起到至关重要的作用。

当前进行土壤属性预测制图的方法主要有3种：1）以土壤发生学为理论基础，以外部环境要素与土壤内在属性协同变化关系为核心的土壤-环境模型[8-10]；2）基于空间信息的土壤属性空间插值预测模型，例如普通克里格插值模型（ordinary kriging，OK）[11-15]；3）综合模型，结合外部环境要素与土壤内在属性及空间信息进行建模，例如协同克里格插值模型（co-kriging，COK）。土壤属性的空间依赖性和异质性为构建土壤属性预测模型提供了理论基础和科学依据，同时也为克里格模型中的半变异函数提供选择依据和准则，为此在构建土壤属性模型的过程中充分考虑土壤属性的空间信息有助于提高模型的精度和可行性。而土壤在形成、转化和侵蚀的过程中受到多种自然环境和人为因素的影响，因此土壤-环境模型的发展也为预测土壤属性的空间分布以及变化过程提供了一定的帮助[16-17]。但是由于克里格模型是借助于半变异函数的权重系数而建立的空间插值模型，因此在地形复杂或者属性变化强烈的区域难以进行准确的建模和预测，并且克里格模型建模过程忽略了外界因素对土壤属性的影响。土壤-环境模型在建模的过程中，由于不同的环境因素对土壤属性的影响机理复杂，并且存在一定的时间滞后性，进而难以通过简单、直接的线性关系对土壤属性进行定量描述。因此，为了更好地揭示SOCD的空间分异规律，需要在建模过程中综合考虑与SOCD相关的外在环境因子以及内在组分的外在反映（如土壤的反射光谱）。

在构建综合模型进行土壤属性预测时，有学者采用回归克里格模型（regression kriging，RK），以光谱信息作为辅助变量，相对于环境变量而言可以更为直接地反映土壤属性，并且模型同时考虑了残差的空间依赖性，进而保证了基于最小二乘准则回归模型的基本假定（残差项相互独立，互不相关）。Ge等[18]选取密西西比河奎特曼县耕地类型的273个土壤样本，探究近红外光谱方法和地统计方法以及两者结合对土壤属性预测精度的影响，进行回归克里格建模和主成分回归建模，结果表明结合了光谱反射率和空间变异性的回归克里格模型效果更好，决定系数2达到了0.65；对于传统回归模型无法准确预测的土壤属性（如钾、钠、磷元素含量），回归克里格模型也能得到较好的预测结果。Bilgili等[19]选取土耳其北部一个32 hm2的研究区域内的土壤样本，进行PLSR、OK、COK、RK分别建模并进行对比分析，结果表明，光谱反射率结合地统计模型的预测效果更好，对土壤有机质的预测效果，COK、RK优于PLSR优于OK。然而，当前少有研究探究上述方法在SOCD预测制图中的应用。

本文从SOCD具有空间依赖性和异质性这一土壤本质特征出发，选取采集自江汉平原的232个土壤样本作为研究对象，尝试以土壤属性的光谱信息作为辅助变量，利用协同克里格模型和回归克里格模型构建SOCD预测模型，同时与普通克里格模型和PLSR模型进行预测精度比较，探讨土壤光谱信息和空间信息在SOCD建模中的作用，以期为SOCD的预测提供有效的参考信息和理论基础。

1 材料与方法

1.1 研究区域概况

汊河镇位于江汉平原中心，地理坐标位于29°55′～30°04′N，113°23′～113°33′E[20]，被选为研究区域。汊河镇的地理面积约为153 km2，海拔范围为2～35 m，属亚热带季风气候，也具有明显的大陆性气候特点，冬夏长，春秋短，四季分明，光照充足，雨量充沛，温和湿润，年均气温为16.6 ℃，年均降雨量达1 154 mm。江汉平原是典型的冲积平原，研究区域适合多种作物生长，是中国的一个重要农业地区。研究区的土壤母质层主要来源是河流冲积和湖泊沉积，土壤类型主要为水稻土和潮土，研究区区位及土壤样本点的空间分布如图1所示。

图1 研究区区位及样本点空间分布图

Fig.1 Location of study area and spatial distribution of sample points

1.2 样本制备与光谱测定

土壤样本的采集工作于2013年7月完成，采集时使用随机布点法布设232个样点，每个样点处在1 m2的方形范围内的4个角及中心处使用木铲采集5份表层土壤样本（0～30 cm），混合均匀后取500 g作为该样点土壤样本，装入自封袋中。此外，取部分土样装入铝盒中，用于实验室土壤含水量的测定。同时使用环刀采集环刀土一份装入自封袋，用于土壤容重分析[20]，样本采集点之间的最小间隔为100 m，其中耕地样本130个、林地29个、园地28个、建设用地39个、荒地6个。

土壤样本在实验室内经过一系列预处理，包括风干、研磨和过0.15 mm筛等，之后分别进行光谱测定和化学方法分析。其中，土壤有机碳含量分析采用的化学方法是重铬酸钾氧化-分光光度法[21]。土壤有机碳密度的计算公式为

式中为土壤发生层数（文中取=1）；θ为第层土壤大于2 mm砾石的体积百分含量，%；p为第层土壤容重，g/cm3；C为第层土壤有机碳含量，g/kg；为第层土壤厚度，cm[20]。

土壤样本在可见光—近红外光谱（350～2 500 nm）区间内的光谱反射率由ASD FieldSpec3地物光谱仪获得，光谱反射率的具体测量步骤与卢延年、陈奕云等的研究类似[2,22]。

1.3 光谱数据预处理

由于受到光谱仪自身误差和测量环境噪声的影响，光谱反射率不可避免地受到随机噪声、基线漂移以及多次散射效应等因素影响，这些因素可能影响最终建立模型的可靠性[4]。因此，光谱预处理是建模前的一个重要步骤。

本研究选取了5种光谱预处理方法，包括Savitzky-Golay平滑方法（S-G）、一阶导数法（1st）和二阶导数法（2nd）、标准正态变量变换处理方法（standard normal variate，SNV）和多元散射校正处理方法（multiplicative seater correction，MSC）[23-26]，以及它们的组合，比较了它们在SOCD的PLSR模型中对预测精度的影响，分别是S-G、S-G+MSC、S-G+SNV、S-G+1st、S-G+2nd、S-G+1st+MSC、S-G+2nd+MSC、S-G+1st+SNV、S-G+2nd+SNV。

1.4 建模方法

1.4.1 偏最小二乘回归

由于光谱波段变量间往往存在多重共线性，直接使用最小二乘法拟合得到的回归方程会产生严重失真。偏最小二乘回归是一种多变量统计数据分析方法，它开辟了一种有效的途径，在处理样本容量小、解释变量多、变量间存在多重共线性问题方法有独特的优势，已成为土壤有机碳等组分估算的常用方法[21,27]。

1.4.2 普通克里格模型

普通克里格法，是一种建立在区域化变量理论上的空间局部插值法，待估计点的值可以根据周围一定范围内观测点的值加权得到。它的权重值是结合观测值的变异函数，在无偏最优估计的思想和拉格朗日极小化原理指导下得到，且往往假设空间为各向同性。具体公式如下

权重取决于领域内样点和目标点的相对位置，半变异函数可以描述数据点各变量的空间相关性和协方差结构，对未知样点进行无偏、最优估计，无偏是指偏差的数学期望为0，最优是指估计值与实际值之差的平方和最小，公式如下

1.4.3 协同克里格模型

协同克里格对普通克里格进行了扩展，主要区别是添加了一个或多个与主变量（1）存在空间相关性的辅助变量（2），具体公式如下

本文的主变量是土壤有机碳密度，辅助变量是土壤可见—近红外光谱反射率。

1.4.4 回归克里格模型

回归克里格法将观测值看作代表确定性部分的趋势项和代表随机性部分的残差项的加和，其中趋势项由外界因素干扰产生，依据最小二乘法（ordinary least square，OLS）原理拟合目标变量和辅助变量的回归方程，并得到各辅助变量参数；残差项代表土壤属性固有的随机性，理论上呈正态分布，可以通过克里格插值得到任意一点的残差。则预测点属性值可由辅助变量加权值与该点残差加和得到[19]。其过程可表示为

1.5 模型评价

为了最大限度的检验模型对未知样点的估测能力，文章选择1∶1的比例来构建建模样本集与验证样本集，即根据Kennard-Stone算法将232个总体样本划分为建模样本集（119个样本）和验证样本集（113个样本）[28-29]。

模型的精度选取决定系数2、均方根误差（root mean squares error，RMSE）、预测均方根误差（root mean squares error of prediction，RMSEP）、标准差与预测均方根误差比（ratio of performance to deviation，RPD）等参数来衡量。RPD是验证样本集SOCD的标准差与预测均方根误差RMSEP的比值，一般认为，RPD小于1.4时，模型难以对样本进行有效预测；RPD介于1.4～2之间，模型可以对样本进行粗略地预测；RPD大于等于2时，模型预测效果极好[22,30-31]。计算公式如下

式中为验证点个数，y为第个样本的测量值，为第个样本的预测值，为测量值的均值。

2 结果与分析

2.1 SOCD描述性统计

土壤总体样本、建模样本集和验证样本集的SOCD数据分布特征基本相近，保证了建模数据集的代表性。标准差和变异系数可以表示土壤样本数据与平均值的离散度，3个数据集的标准差分别为1.37、1.30和1.40 kg/m2，变异系数分别为29.70%、29.83%和28.39%（表1），三者之间的标准差和变异系数差距很小，保证了数据之间离散程度的一致性。3个数据集的偏度系数分别为0.03、0.06和−0.08，峰度系数分别为−0.72、−0.52和−0.89（表1），均接近于0，这表明3个数据集中的土壤有机碳密度的分布特征符合正态分布特征，说明建模数据可以满足克里格插值模型所要求的二阶平稳性，保证了建模结果的准确可靠性。

表1 不同样本集土壤有机碳密度的基本统计特征

2.2 PLSR建模中光谱数据预处理效果

不同光谱预处理条件下的模型评价结果如表2所示。对未经预处理的原始光谱（即反射率光谱）进行建模，可以得到建模集决定系数（2ofcalibration，2-Cal）为0.74，留一交叉验证决定系数2-CV（2of leave-one-out cross validation）为0.603，验证集决定系数（2ofprediction，2-Pred）为0.558。这说明光谱反射率对SOCD的变异具有较好的指示作用。由于原始光谱存在的噪声、漂移因素对建模存在一定的干扰，因此对原始光谱进行合适的预处理可以进一步提高模型的预测精度。单纯地采用Savitzky-Golay平滑方法，或者在对原始光谱进行Savitzky-Golay平滑的基础上，结合标准正态变换（SNV）或多元散射校正（MSC），建立的模型精度未有明显提高。而对光谱数据进行一阶和二阶微分预处理后再结合S-G、SNV、MSC等预处理方法进行建模，2-Cal可达0.909，建模精度有了明显的提高，并且模型主成分数为4，与无预处理模型的8个主成分数相比也有了明显的降低，这说明一阶和二阶微分方法对光谱数据的预处理起着至关重要的作用。预处理之后的土壤光谱与SOCD的皮尔逊相关系数（Pearson’s coefficient）绝对值的最大值有明显提高，突出了光谱特征波段与SOCD之间的相关关系，进而可以使用较少的光谱主成分包含更多的SOCD变异信息（图2）。综合考虑建模和留一交叉验证精度（所建模型需要对建模数据变异具有良好的解释能力，即较高的2-Cal和2-CV）以及验证样本集检验精度（即模型需要具有良好的预测能力，如RPD>1.4）。因此，认为Savitzky-Golay平滑处理、一阶微分和标准正态变换的组合是最佳预处理方法。

2.3 SOCD预测模型的建立

2.3.1 利用PLSR构建SOCD预测模型

利用S-G+1st+SNV预处理方法对土壤光谱反射率进行变换之后，采用PLSR方法建立SOCD预测模型，模型的前4个主成分变量可以解释80%以上的光谱数据信息，贡献率分别为47.36%、9.63%、16.18%和8.04%（表3），同时利用皮尔逊相关系数来验证主成分变量与SOCD之间的关系，相关系数分别为0.688、0.310、0.402和0.284，值均满足小于0.01，这说明光谱主成分变量与SOCD之间均表现出正相关的关系，且第一主成分（principal component1，PC1）与SOCD之间的相关性最高，第四主成分（principal component4，PC4）的相关性最低，这主要是由于不同的主成分变量包含不同的波段信息，而不同位置的波段信息对土壤中的不同组分具有不同程度的响应。由上节可知，基于光谱信息，利用S-G+1st+SNV预处理方法进行PLSR建模，能够对SOCD进行较好的预测，标准差与预测均方根误差比值RPD为1.523，2-Pred为0.605。

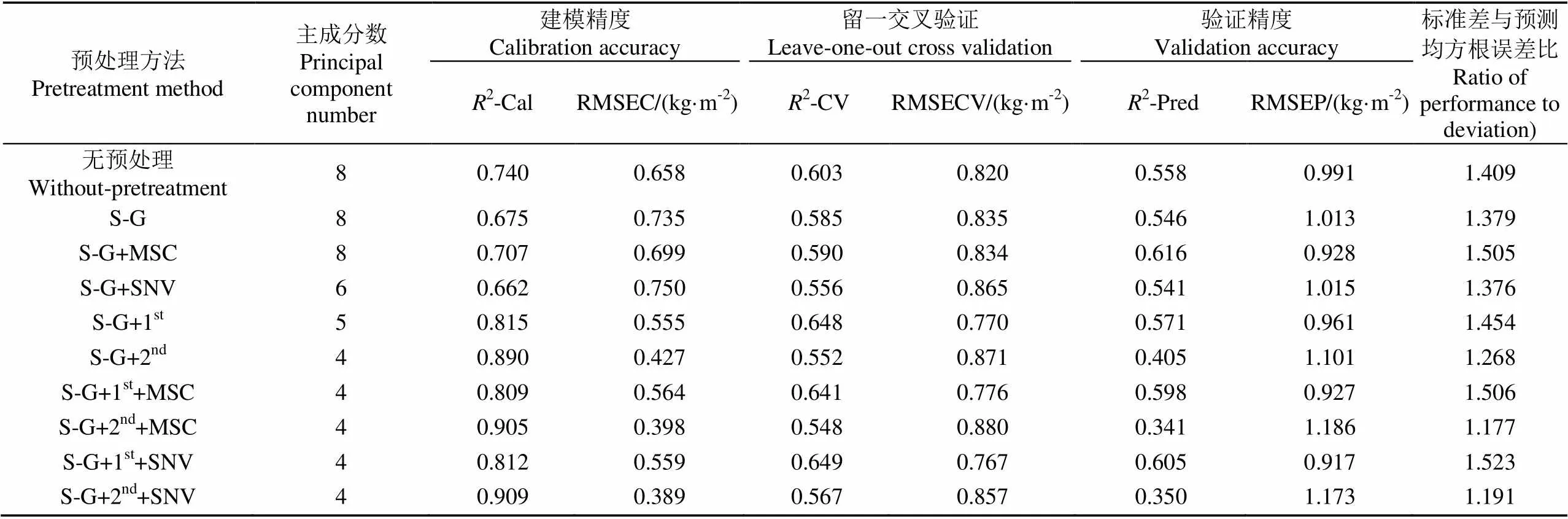
表2 基于不同预处理方法的PLSR模型及检验结果

注：S-G: Savitzky-Golay 平滑处理；1st、2nd：一阶、二阶微分处理；SNV：标准正态变换；MSC：多元散射校正处理；2-Cal：建模集决定系数；RMSEC：建模集均方根误差；2-CV：留一交叉验证决定系数；RMSECV：留一交叉验证均方根误差；2-Pred：验证集决定系数；RMSEP：预测均方根误差，下同。

Note: S-G: Savitzky-Golay smoothing; 1st, 2nd: first-order and second-order differential equation; SNV: standard normal variate; MSC: multiplicative seater correction;2-Cal:2of calibration; RMSEC: root mean squares error of calibration;2-CV:2of leave-one-out cross validation; RMSECV: root mean squares error of leave-one-out cross validation;R-Pred:2of prediction; RMSEP: root mean squares error of prediction, the same as below.

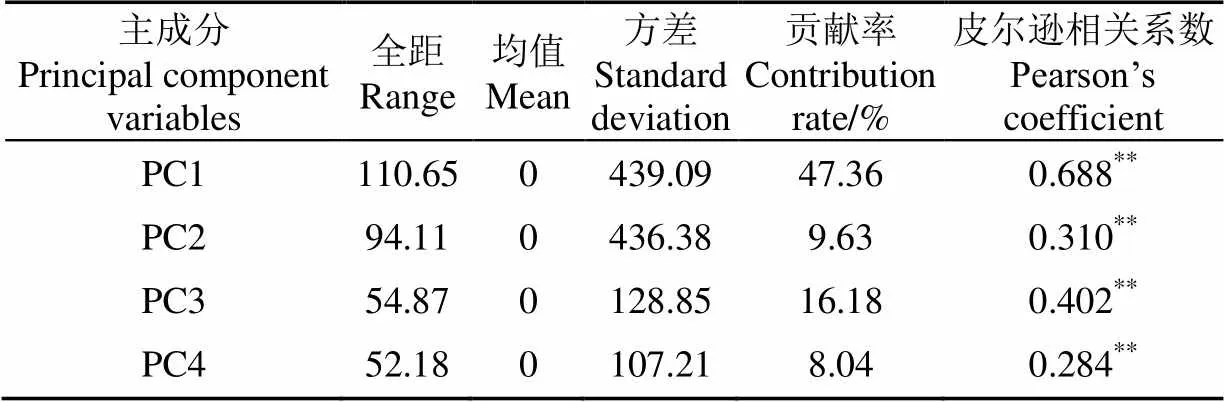
表3 样本光谱信息主成分的基本统计

注：**为在0.01水平（双侧）上显著。PC1、PC2、PC3、PC4分别为样本光谱信息的第一、二、三、四主成分，下同。

Note: ** means significant at 0.01 level (double sides). PC1, PC2, PC3, PC4 represent the first, second, third, and the forth principal component of sample spectra, respectively, the same as below.

2.3.2 利用OK模型和COK模型构建SOCD预测模型

考虑土壤属性具有空间变异性，对SOCD实测值进行普通克里格插值分析，其中半变异函数拟合模型采用指数函数，块基比参数0/(0+)为59.32%，介于25%～75%之间，具有中等程度空间相关性[32]。验证集决定系数2-Pred仅为0.004（表4），说明普通克里格模型对于SOCD预测结果精度并不理想。这主要是由于样点布设时采用随机布点法，未有SOCD的空间变异信息作为先验知识，导致样本密度不尽合理，进而影响OK模型的预测结果，普通克里格模型虽然考虑了变量的空间变异性，但对样点本身数据质量依赖性较强。

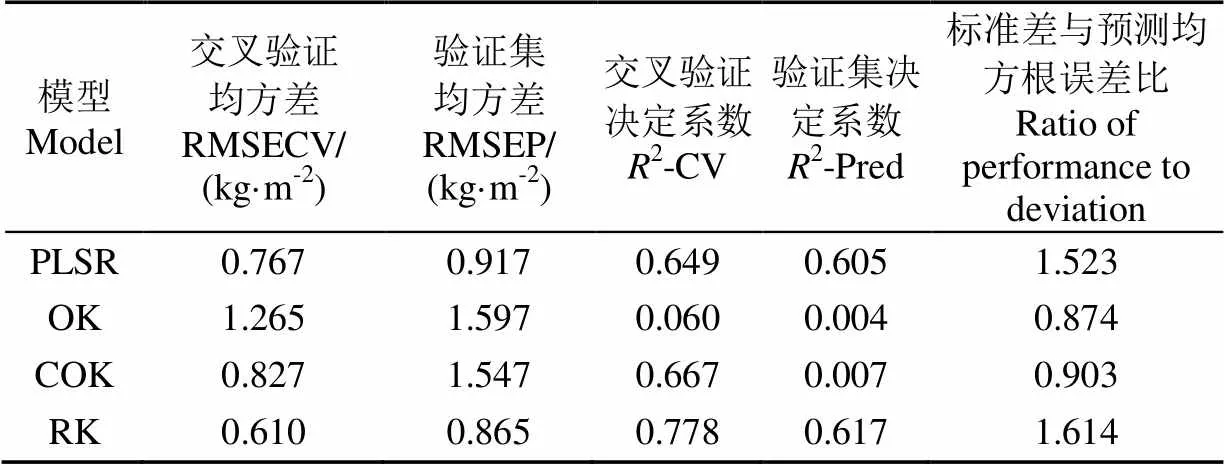
表4 PLSR、OK、COK及RK 4种方法的精度评价指标对比

注：PLSR：偏最小二乘回归模型，OK：普通克里格模型，COK：协同克里格模型，RK：回归克里格模型，下同。

Note: PLSR: partial least-squares regression model, OK: ordinary kriging model, COK: co-kriging model, RK: regression kriging model, the same as below.

根据光谱数据主成分与SOCD的皮尔逊相关系数，选取第一、二、三主成分作为辅助变量，以SOCD为主变量进行协同克里格插值，SOCD与各协同变量的半变异函数模型显示，块基比分别为34.20%、23.49%、37.09%（表5），第一、三辅助变量的块基比介于25%～75%之间，具有中等程度空间相关性，第二辅助变量的块基比小于25%，具有较强空间相关性[32]，交叉验证决定系数为0.667（表4），建模集模型拟合度较好，这主要是由于土壤光谱反射率与SOCD相关性较强，可以提供有价值的辅助信息，在SOCD预测建模中起重要作用。但是由于COK模型对样本密度均一性有一定要求，并且在模型预测过程中，未能结合预测集样本光谱信息，致使预测精度不理想，2-Pred仅为0.007（表4）。

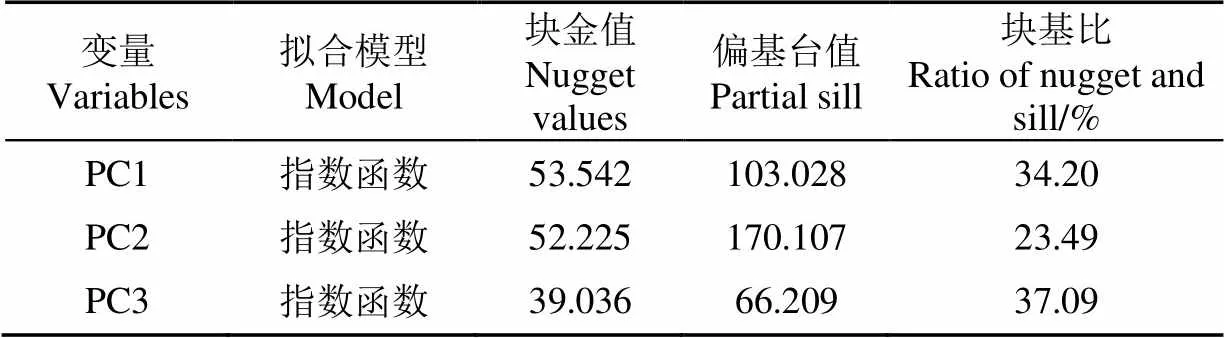
表5 协同克里格模型参数

2.3.3 利用RK模型构建SOCD预测模型

在利用RK模型构建SOCD预测模型的过程中，使用OLS得到模型残差范围为−1.29～1.24kg/m2，残差值主要集中在0左右，偏度系数为−0.116，峰度系数为−0.369，通过Kolmogorov-Smirnov检验符合正态分布，适合进行克里格插值（图3a）。对残差进行普通克里格插值，半变异函数模型采用指数函数模型，块基比为27.12%，接近25%，具有较高的空间相关性[32]（图3b）。回归克里格模型作为SOCD预测模型具有较高的验证精度，2-Pred为0.617（表4）。土壤是变异性极强的连续体，空间非平稳性的存在导致OLS这一类全局模型无法捕捉到土壤变异的局部特征，利用克里格法对代表随机性的残差进行插值，插值结果能揭示可能被空间非平稳性所掩盖的一些局部变化，反映出更加真实的土壤属性空间变异情况。

2.4 验证与评价SOCD预测模型

留一交叉验证结果表明RK模型具有最好的建模精度，建立的模型能解释建模集SOCD 77.8%的变异，而COK和PLSR次之，2-CV分别为0.667和0.649，OK模型最差，2-CV仅为0.06（表4）。OK模型的预测精度较差，这主要是由于样点布设时采用随机布点法，未有SOCD的空间变异信息作为先验知识，导致样本密度不尽合理，进而影响OK模型的预测结果；同时在小区域尺度中，受到土壤属性空间复杂程度以及变程多样性的影响，OK模型并不能保证半变异函数模型可以完全模拟真实的土壤属性空间结构特征。光谱反射率作为土壤属性的直接反应可以提供有价值的辅助信息来模拟SOCD的空间分布特征，在SOCD预测建模中起到重要的作用，这也是以土壤光谱反射率为自变量的PLSR模型和以土壤光谱反射率为辅助变量的COK模型在预测精度方面优于OK模型的主要原因。对于多元线性回归模型而言，一旦预测残差具有空间结构，就说明因变量的部分变异未能被模型所解释，为此本研究选用RK模型来减少残差结构对于预测结果的影响。结果表明RK模型具有相对较高的预测精度，这也体现了在建立土壤属性多元线性回归模型时考虑残差空间特征的必要性。

3 讨 论

土壤有机碳储量与气候、成土母质、土壤生物、地形、成土时间等环境因素以及人类活动密切相关，土壤有机碳具有空间依赖性和空间异质性，进而导致土壤有机碳空间分布的不确定性，影响土壤有机碳密度计算和土壤有机碳储量估算的精度。

土壤光谱是与SOCD相关的土壤内在组分与外部因素的代理变量，光谱反射率可以直接反映土壤的物理结构及化学特征，光谱反射率也可以通过某一波段的光谱特征来反映相对应的SOCD。文中考虑到土壤光谱信息进行建模，相比于OK模型，以土壤光谱反射率为自变量的PLSR模型和以土壤光谱反射率为辅助变量的COK模型预测效果更好，并且与前人的研究结果相一致[19]，说明借助于光谱反射率作为辅助信息在一定程度上可以提高模型的预测精度，光谱反射率在土壤属性预测建模中起重要作用。

土壤本身是一个开放的复杂系统，由于受复杂的成土过程、自然环境要素以及人类活动等因素的影响，在不同的地区SOCD存在各具特点的空间分异规律，表现出一定的空间异质性。结合光谱信息和SOCD的空间分布信息构建的COK模型，建模集的2-CV为0.667，高于仅考虑光谱信息进行建模的PLSR模型（2-CV=0.649），说明SOCD的空间信息可以提高模型的建模精度，但是由于克里格模型是借助于半变异函数的权重系数而建立的空间插值模型，在地形复杂或者属性变化强烈的区域难以进行准确的预测，并且会忽略外界影响因素对土壤属性的影响和作用，因而本研究中的COK模型的预测精度低于PLSR模型。

由于预测残差空间自相关性的存在，难以保证通过PLSR模型得到的预测结果具有无偏性和独立性，为此考虑在构建基于光谱的土壤属性预测模型时，尽量地减少残差对结果的影响，有助于模型精度的提高。文中RK模型的建模精度（2-CV=0.778）和预测精度（2-Pred=0.617）均高于PLSR模型（2-CV=0.649，2-Pred=0.605），说明同时考虑光谱反射率和土壤属性的空间特性可以提高预测精度，考虑多元线性回归模型残差的空间结构能够更加真实的反映出土壤属性的空间变异情况。

研究表明，PLSR模型预测效果（2-Pred=0.605）优于OK模型（2-Pred=0.004），这两种模型均可以低成本地预测土壤属性，但是都具有一定的缺点，OK模型是一种基于样点空间依赖性的局部预测方法，PLSR模型虽可以进行大尺度全局预测，但是精准的预测结果需要以土壤变量具有较宽的测定范围值以及变量与土壤反射光谱具有直接相关性为前提，具有一定的局限性。克里格法的前提是假设数据来自平稳的随机过程，然而研究区域具有特殊性，受人为活动的影响，SOCD的分布并非随机过程，因此OK和COK模型未能很好的预测结果，PLSR和RK模型则充分利用了未知样点的光谱这一获取便捷的先验信息，因此对未知样点的SOCD估算效果较好。光谱反射率作为COK和RK模型中重要的辅助变量，光谱数据的预处理过程对土壤属性的预测结果有极大的影响，之后的研究需要进行更多的实验来选出最佳预处理方法。

此外，本文对SOCD进行估测时，没有对不同土地利用类型的土壤进行区分，只是根据各种地类的面积，确定不同地类上采样点的个数以确保样本集的全面性与准确性，而不同地类对应不同的土壤类型，也意味着不同的SOCD值，以后的研究可以进一步探索SOCD在不同地类上的分布规律。

4 结 论

本文借助于土壤可见—近红外反射光谱（400～2 350 nm），构建了偏最小二乘回归、普通克里格、协同克里格、回归克里格模型，进行土壤有机碳密度预测精度对比分析。考虑了光谱反射率的空间结构特征，以及多元线性回归模型残差的空间结构，从不同的角度和方向来尽可能的提高空间模型的预测精度和准确度，得出以下结论：

1）偏最小二乘回归模型（partial least squares regression，PLSR）中光谱数据预处理采用平滑处理、一阶微分和标准正态变换的组合时结果最佳，留一交叉验证决定系数（2of leave-one-out cross validation，2-CV）值为0.649，模型的标准差与预测均方根误差比（ratio of performance to deviation，RPD）值为1.523，均达到最高值，优于其他预处理方法。

2）当选用光谱反射率作为协同克里格模型（co-kriging，COK）的辅助变量时，在一定程度上可以提高模型的建模精度。同时考虑多元线性回归模型残差的空间特征，对提高模型的预测精度也起到重要的作用，因此，回归克里格模型（regression kriging，RK）具有最高的预测精度（2-Pred=0.617）。

[1] 潘根兴，赵其国. 我国农田土壤碳库演变研究：全球变化和国家粮食安全[J]. 地球科学进展，2005，20(4)：384－393. Pan Genxing, Zhao qiguo. Study on evolution of organic carbon stock in agricultural soils of China: Facing the challenge of global chance and food security[J]. Advances in Earth Science, 2005, 20(4): 384－393. (in Chinese with English abstract)

[2] 卢延年，刘艳芳，陈奕云，等. 江汉平原土壤有机碳含量高光谱预测模型优选[J]. 中国农学通报，2014，30(26)：127－133. Lu Yannian, Liu Yanfang, Chen Yiyun, et al. Optimization of the hyperspectral prediction model of soil organic carbon contents of Jianghan plain[J]. Chinese Agricultural Science Bulletin, 2014, 30(26): 127－133. (in Chinese with English abstract)

[3] 王绍强，周成虎. 中国陆地土壤有机碳库的估算[J]. 地理研究，1999，18(4)：349－356. Wang Shaoqiang, Zhou Chenghu. Estimating soil carbon reservior of terrestrial ecosystem in China[J]. Geographical Research, 1999, 18(4): 349－356. (in Chinese with English abstract)

[4] 张小超，吴静珠，徐云. 近红外光谱分析技术及其在现代农业中的应用[M]. 北京：电子工业出版社，2012：95－140.

[5] 陈涛，常庆瑞，刘京. 基于光谱信息辅助的污灌区农田土壤镉协同克里格分析[J]. 光谱学与光谱分析，2013，33(8)：2157－2162. Chen Tao, Chang Qingrui, Liu Jing. Study of spatial interpolation of soil Cd contents in sewage irrigated area based on soil spectral information assistance[J]. Spectroscopy and Spectral Analysis, 2013, 33(8): 2157－2162. (in Chinese with English abstract)

[6] 李耀翔，汪洪涛，耿志伟，等. 基于近红外光谱及BP神经网络分析法预测森林土壤有机碳含量[J]. 西部林业科学，2014，43(3)：1－6. Li Yaoxiang, Wang Hongtao, Geng Zhiwei, et al. Prediction of forest soil organic carbon content based on NIRS and BP neural network[J]. Journal of West China Forestry Science, 2014, 43(3): 1－6. (in Chinese with English abstract)

[7] 李耀翔，汪洪涛，耿志伟，等. 基于NIR及PLS-PCR-SVR预测森林土壤有机碳含量[J]. 安徽农业科学，2014，42(15)：4702－4706. Li Yaoxiang, Wang Hongtao, Geng Zhiwei, et al. Prediction of forest soil carbon content based on the near infrared spectroscopy and PLS-PCR-SVR[J]. Journal of Anhui Agricultural Sciences, 2014, 42(15): 4702－4706. (in Chinese with English abstract)

[8] 王绍强，刘纪远，于贵瑞. 中国陆地土壤有机碳蓄积量估算误差分析[J]. 应用生态学报，2003，14(5)：797－802. Wang Shaoqiang, Liu Jiyuan, Yu Guirui. Error analysis of estimating terrestrial soil organic carbon storage in China[J]. Chinese Journal of Applied Ecology, 2003, 14(5): 797－802. (in Chinese with English abstract)

[9] 邵月红，潘剑君，许信旺，等. 浅谈土壤有机碳密度及储量的估算方法[J]. 土壤通报，2006，37(5)：1007－1011. Shao Yuehong, Pan Jianjun, Xu Xinwang, et al. Discussion on the methods for estimating soil organic carbon density and storage[J]. Chinese Journal of Soil Science, 2006, 37(5): 1007－1011. (in Chinese with English abstract)

[10] 吴瑾，吴克宁，赵华甫，等. 土壤有机碳储量估算方法及土地利用调控措施研究进展[J]. 中国土地科学，2010，24(10)：18－24. Wu Jin, Wu Kening, Zhao Huafu, et al. Review on the methods of soil organic carbon storage estimation and land use control measures[J]. China Land Science, 2010, 24(10): 18－24. (in Chinese with English abstract)

[11] 顾成军. 克里格插值在区域土壤有机碳空间预测中的应用[J]. 中国土壤与肥料，2014(3)：93－97. Gu Chengjun. Application of kriging method in spatial prediction of regional soil organic carbon[J]. Soil and Fertilizer Sciences in China, 2014(3): 93－97. (in Chinese with English abstract)

[12] 郭龙，张海涛，陈家赢，等. 基于协同克里格插值和地理加权回归模型的土壤属性空间预测比较[J]. 土壤学报，2012，49(5)：1037－1042. Guo Long, Zhang Haitao, Chen Jiaying, et al. Comparison between co-kriging model and geographically weighted regression model in spatial prediction of soil attributes[J]. Acta Pedologica Sinica, 2012, 49(5): 1037－1042. (in Chinese with English abstract)

[13] 杨顺华，张海涛，郭龙，等. 基于回归和地理加权回归Kriging的土壤有机质空间插值[J]. 应用生态学报，2015，26(6)：1649－1656. Yang Shunhua, Zhang Haitao, Guo Long, et al. Spatial interpolation of soil organic matter using regression kriging and geographically weighted regression kriging[J]. Chinese Journal of Applied Ecology, 2015, 26(6): 1649－1656. (in Chinese with English abstract)

[14] 姜勇，梁文举，李琪. 利用与回归模型相结合的克里格方法对农田土壤有机碳的估值及制图[J]. 水土保持学报，2005，19(5)：99－102. Jiang Yong, Liang Wenju, Li Qi. Prediction and Mapping of Soil Organic Carbon in Farmland Using Kriging Combined with Regression[J]. Journal of Soil and Water Conservation, 2005, 19(5): 99－102. (in Chinese with English abstract)

[15] 代富强，周启刚，刘刚才. 基于回归克里格和遥感的紫色土区土壤有机质含量空间预测[J]. 土壤通报，2014，45(3)：562－567. Dai Fuqiang, Zhou Qigang, Liu Gangcai. Spatial prediction of soil organic matter contents in a purplish soil region with regression Kriging and remote sensing[J]. Chinese Journal of Soil Science, 2014, 45(3): 562－567. (in Chinese with English abstract)

[16] 张忠启，于法展. 土壤类型信息在土壤有机碳空间预测中的应用研究[J]. 中国农学通报，2013，29(11)：139－144. Zhang Zhongqi, Yu Fazhan. Study on the application of soil type information in spatial prediction of soil organic carbon[J]. Chinese Agricultural Science Bulletin, 2013, 29(11): 139－144. (in Chinese with English abstract)

[17] 邓祥征，姜群鸥，林英志，等. 中国农田土壤有机碳贮量变化预测[J]. 地理研究，2010，29(1)：93－101. Deng Xiangzheng, Jiang Qunou, Lin Yingzhi, et al. Simulation of the changes of soil organic carbon stock of cropland in China[J]. Geographical Research, 2010, 29(1): 93－101. (in Chinese with English abstract)

[18] Ge Y, Thomasson J A, Morgan C L, et al. VNIR diffuse reflectance spectroscopy for agricultural soil property determination based on regression-kriging[J]. Transactions of the ASABE, 2007, 50(3): 1081－1092.

[19] Bilgili A V, Akbas F, Es H M V. Combined use of hyperspectral VNIR reflectance spectroscopy and kriging to predict soil variables spatially[J]. Precision Agriculture, 2011, 12(3): 395－420.

[20] Liu Yaolin, Guo Long, Jiang Qinghu, et al. Comparing geospatial techniques to predict SOC stocks[J]. Soil & Tillage Research, 2015(148): 46－58.

[21] 梁重山，党志，刘丛强. 土壤沉积物样品中有机碳含量的快速测定[J]. 土壤学报，2002，39(1)：129－133. Liang Chongshan, Dang Zhi, Liu Congqiang. Rapid determination of total organic carbon in soil/sediment samples[J]. Acta Pedologica Sinica, 2002, 39(1): 129－133. (in Chinese with English abstract)

[22] 陈奕云，漆锟，刘耀林，等. 顾及土壤湿度的土壤有机质高光谱预测模型传递研究[J]. 光谱学与光谱分析，2015，35(6)：1705－1708.

Chen Yiyun, Qi Kun, Liu Yaolin, et al. Transferability of Hyperspectral Model for Estimating Soil Organic Matter Concerned with Soil Moisture[J]. Spectroscopy and Spectral Analysis.2015, 35(6): 1705－1708. (in Chinese with English abstract)

[23] Shi Tiezhu, Chen Yiyun, Liu Yaolin, et al. Visible and near-infrared reflectance spectroscopy—An alternative for monitoring soil contamination by heavy metals[J]. Journal of Hazardous Materials, 2014, 265(2): 166－176.

[24] Rinnan A, Berg F V D, Engelsen S B. Review of the most common pre-processing techniques for near-infrared spectra[J]. Trac-Trends in Analytical Chemistry, 2009, 28(10): 1201－1222.

[25] Liu Yaolin, Chen Yiyun. Estimation of total iron content in floodplain soils using VNIR spectroscopy—a case study in the Le’an River floodplain, China[J]. International Journal of Remote Sensing, 2012, 33(18): 5954－5972.

[26] Wold S , Kettaneh-Wold N , Skagerberg B. Nonlinear PLS modeling[J]. Chemometrics and Intelligent Laboratory Systems, 1989, 7(1/2): 53－65.

[27] Haaland D M, Thomas E V. Partial least-squares methods for spectral analyses. 1. Relation to other quantitative calibration methods and the extraction of qualitative information[J]. Analytical Chemistry, 1988, 60(11): 1193－1202.

[28] Kennard R W, Stone L A. Computer aided design of experiments[J]. Technometrics, 1969, 11(1): 137－148.

[29] 刘艳芳，卢延年，郭龙，等. 基于地类分层的土壤有机质光谱反演校正样本集的构建[J]. 土壤学报，2016，53(2)：332－341.

Liu Yanfang, Lu Yannian, Guo Long, et al. Construction of calibration set based on the land use types in visible and Near-InfRared (VIS-NIR) model for soil organic matter estimation[J]. Acta Pedologica Sinica, 2016, 53(2): 332－341. (in Chinese with English abstract)

[30] 于雷，洪永胜，耿雷，等. 基于偏最小二乘回归的土壤有机质含量高光谱估算[J]. 农业工程学报，2015，31(14)：103－109.

Yu Lei, Hong Yongsheng, Geng Lei, et al. Hyperspectral estimation of soil organic matter content based on partial least squares regression[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(14): 103－109. (in Chinese with English abstract)

[31] Shi Tiezhu, Cui Lijuan, Wang Junjie, et al. Comparison of multivariate methods for estimating soil total nitrogen with visible/near-infrared spectroscopy[J]. Plant and Soil, 2013, 366(1): 363－375.

[32] Johnson R A, Wichern D W. Applied multivariate statistical analysis[M]. New Jersey: Prentice Hall, 2002: 425－430.

Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance

Liu Yanfang1,2,3, Song Yuling1,2,3, Guo Long4, Chen Yiyun1,2,5,6※, Lu Yannian1,2,3, Liu Yi1,2,3

(1.430079; 2.430079; 3.,,,430079,; 4.,,430070,; 5.,430079,; 6.,215123,)

The availability of soil organic carbon density (SOCD) information is of great importance for the development of ecological agriculture and the study of global climate change. Compared with traditional laboratory analysis, Visible and near-infrared (VNIR) reflectance spectroscopy has proven to be a rapid, non-destructive and cost effective method for estimating a variety of soil properties. It has got rapid development and has been applied in the field of soil research. In the prediction of soil properties by using spectral information, however, traditional linear regression models often ignore the spatial heterogeneity and dependency of soil, and fail to consider the spatial structure of the error term. With the aims to fill the current gap, a total of 232 topsoil samples were collected in Jianghan Plain with their spectral reflectance and SOCD measured. Partial least squares regression (PLSR), ordinary kriging (OK), co-kriging (COK), and regression kriging (RK) were used to estimate SOCD by using differently pre-treated spectral reflectance. Due to the facts that spectral pretreatments are crucial to reduce the physical variability and particle size effect, and are helpful to remove both additive and multiplicative effects in the spectra, five combinations of spectral pretreatments were utilized while predicting SOCD with PLSR. They were Savitzky-Golay smoothing (S-G), S-G + Multiplicative Scatter Correction (MSC), S-G+Standard Normal Variate (SNV), S-G + first derivative (1st), S-G + second derivative (2nd), S-G+1st+MSC, S-G+2nd+MSC, S-G+1st+SNV, S-G+2nd+SNV. The prediction capabilities of the models were evaluated byR, root mean squared error (RMSE), and ratio of performance to deviation (RPD). Results showed that the RK approach which utilized soil spectra information outperformed the others, with the highestR-Pred 0.617 and RPD 1.614, and the lowest RMSEP 0.865 kg/m2. PLSR took the second place withR-Pred 0.605, RPD 1.523 and RMSEP 0.917 kg/m2, which was also acceptable for SOCD prediction. COK and OK generally failed in the predictions of SOCD, withR-Pred equaled to 0.007 and 0.004, RPD equaled to 0.903 and 0.874 and RMSEP equaled to 1.547 and 1.597 kg/m2, respectively. Results indicated that the RK model, which considered both the spectral reflectance and the spatial structure of the error term of multivariate linear regression model can improve the prediction accuracy of SOCD. The fundamental reasons could be that soil spectra are comprehensive reflections of soil properties and those environmental factors that influence the formation of soil. Therefore, soil spectra are related with the variation of SOCD, and could be helpful in the prediction of SOCD. Besides, the optimal spectral pretreatment for PLSR modelling of SOCD is the combination of smoothing, first-order derivation and SNV. In summary, soil reflectance spectra in the visible and near-infrared region (350-2 500 nm) could serve as an effective proxy variable for SOCD estimation. Given that soil VNIR reflectance spectra are easy and quick to measure, and the measurement is also environmentally friendly, we would like to argue that soil spectral reflectance could serve as an ideal auxiliary variable for the spatial interpolation of SOCD.

soils; models; spectrum analysis; soil organic carbon density; partial least-squares regression; co-kriging; regression kriging

10.11975/j.issn.1002-6819.2017.02.025

S151.9+5

A

1002-6819(2017)-02-0183-09

2016-05-10

2016-10-22

国家自然科学基金项目（41501444）；苏州市应用基础农业项目（SYN201422）；中央大学基础研究基金（2662016QD032）

刘艳芳，女，湖北武汉人，教授，博士，主要从事区域规划和经济地理研究及地理信息应用工程的研究工作。武汉 武汉大学资源与环境科学学院，430079。Email：yfliu610@163.com

陈奕云，男，福建泉州人，副教授，研究方向为土壤遥感与地理信息科学。武汉 武汉大学资源与环境科学学院，430079。 Email：chenyy@whu.edu.cn

刘艳芳，宋玉玲，郭 龙，陈奕云，卢延年，刘 以. 结合高光谱信息的土壤有机碳密度地统计模型[J]. 农业工程学报，2017，33(2)：183－191. doi：10.11975/j.issn.1002-6819.2017.02.025 http://www.tcsae.org

Liu Yanfang, Song Yuling, Guo Long, Chen Yiyun, Lu Yannian, Liu Yi. Geostatistical models of soil organic carbon density prediction based on soil hyperspectral reflectance[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2017, 33(2): 183－191. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2017.02.025 http://www.tcsae.org