基于实物期权的分布式风电站投资策略研究
黄守军,余 波,张宗益
(1.中山大学岭南(大学)学院,广东 广州 510275;2.重庆大学经济与工商管理学院,重庆 400030)
基于实物期权的分布式风电站投资策略研究
黄守军1,余 波2,张宗益2
(1.中山大学岭南(大学)学院,广东 广州 510275;2.重庆大学经济与工商管理学院,重庆 400030)
考虑分布式发电的优先自用特征与风电站的经济特性,在贡献毛益随机变动前提下,运用实物期权理论构建了分布式风电站投资机会的期权定价模型。求解出贡献毛益临界值、最优投资规模、以及延迟投资的期权价值和期望等待时间,通过算例分析验证了主要结论并给出了参数对均衡状态影响程度的变动规律。研究发现:对投资有时限的分布式风电站而言,贡献毛益临界值、最优投资规模、以及期望等待时间均与贡献毛益的期望增长率和变动率正相关,而延迟投资的期权价值与此二者相关性存在差异,且影响的显著性也不同;在一定条件和贡献毛益波动范围内,推迟投资的期权价值与相应的期望等待时间随风电自用占比或初始贡献毛益的增大而分别增大和减小,但风电自用占比对最优投资规模,以及初始贡献毛益对贡献毛益临界值与最优投资规模并无影响;决策者的最优投资决策需同时考虑贡献毛益临界值及其最优投资规模。
分布式风电;实物期权;贡献毛益临界值;投资规模;期望等待时间
1 引言
在国家“风电发展兼顾大基地和分布式发展”的政策信号下,过去5年风电场投资的热点已从原来的陆上风电大基地转向海上风电和内陆中小型分布式风电站。据《“十二五”可再生能源发展规划》拟定的1亿kW风电装机目标,分布式风电到2015年装机将达到3000万kW。经测算,在低风速和高海拔地区开发风电场,其在设备上的投入约为8000元/kW。继分布式光伏发电之后,分布式风电成为了国家力推的又一项发电模式[1]。与大规模集中式开发的风电站不同的是,分布式风电一般规模较小,一般不需要集电线路和电力升压站系统,直接就近并入当地同电压等级电网。适用于靠近用电负荷中心的内陆地区,突出优点就是利于就地并网、就地消纳。此外,所发电量优先自用,富余电量按照当地燃煤脱硫机组标杆电价卖给电网公司,同时电网公司以当地销售目录电价收取下网电量电费。风电站投资利润取决于自用和外售两种情形的收益与成本;另一方面,分布式发电技术、储能技术以及智能电网技术正处于推广应用阶段,并网标准、上网电价实施细则以及政府扶持措施等仍在完善中,而在现实中这些问题就显得至关重要[2]。在分布式风电站投资的诸多决策问题中,对最优时机与规模的选择是研究中很重要的问题之一。
由于分布式风力发电具有投资块性(Lump),建设周期长,沉淀部分大,电价以及贡献毛益面临较大不确定性等特征,因而适用于采用不确定条件下的不可逆投资理论即实物期权(Real options,ROs)方法进行分析[3]。实物期权是从金融期权的概念发展而来的,而金融期权是指赋予其购买者在规定期限内按双方约定的价格购买或出售一定数量潜含金融资产(Underlying financial assets)或标的资产权利的合约。实物期权是金融期权在实体投资领域中的延伸,且核心思想是不确定性可以增加企业投资的价值,期权的所有者可以延迟选择是否对这些资产进一步投资,使资产贬值的风险最小化并保持实物资产收益的稳定性。对实物期权理论建模的经典文献要首推McDonald和Siegel[4]以及Pindyck[5]。不同的是前者的讨论是离散的,而后者的讨论是连续的。之后,Quigg[6]对此作了实证研究,并证实了等待期权所具有的价值。虽然并不是专门针对分布式风电站而做出的,但这些研究是利用实物期权对有关投资策略问题所做的一般性研究。企业在进行投资决策时通常面临3大基本选择,即投资战略、投资时机与投资规模。Dixit和Pindyck[7]首次分析了不可逆条件下,不确定性对企业投资时机的影响,为采用实物期权方法研究企业投资决策问题提供了基本分析框架,此后的研究主要集中在企业最优投资时机和投资战略选择上。然而企业在进行投资决策时,除了投资战略和投资时机选择外,选择合适的投资规模也同样重要[8]。
近年来,国内外众多学者将实物期权理论广泛应用于不确定环境下可再生能源发电决策的研究中。例如,Fleten等[9]假设天然气分布式发电长期成本及电价均为随机变量,求解微电网投资临界值进而得到相对于发电成本,高电价波动延迟投资的同时增加投资期权价值;Bøckman等[10]针对受不确定电价影响的小水电项目提出了一种评价方法,研究发现当电价低于某一限制值时,投资永远都不会是最优选择。相反,则立即投资,且由最优规模函数计算发电容量;刘国中等[11]发展了能够处理多种不确定性因素的发电投资决策框架,用仿真算例对所提出的模型和方法进行了说明,并比较分析了不同场景下的投资决策结果;刘敏和吴复立[12]考虑风了电上网电价的不确定性、风电场投资及运行成本、投资政策(包括项目经营期限、合同期、上网电价的确定、CDM项目等)以及投资时机等因素,建立了适用于中国风电投资环境的风电项目投资决策模型。算例分析表明该模型可为投资者选择合适的投资时机提供决策参考,另外还可作为政策制定者制定合理投资政策的量化分析工具;钟渝等[13]在建设成本和上网电价不确定的情况下,分析了光伏并网发电项目的特点并研究发电企业的最佳投资时机。在此基础上,根据发电企业延迟投资的等待时间得到成本补偿比例,进一步分析得出政府光伏并网发电的成本补偿策略;Boomsma等[14]分析了在政府不同的上网电价和可再生能源证书交易支持计划下,可再生能源项目的最优投资时机和容量选择。研究结论表明上网电价促使投资提前,而决策者一旦实施了投资,则可再生能源证书交易有利于扩大项目发电容量。在这些研究中,投资机会类似于一个没有确定到期日期的看涨期权,因而投资决策就相当于决定是否执行这一看涨期权,执行价格就是投资成本。这正是已有文献及本文建模的基本思想。
总的来说,从目前已有的文献来看,针对分布式风电站投资行为进行均衡决策分析的研究并不多,且国内外主流研究都长期忽视了对最优投资时机可达性问题的讨论。其次,分布式发电的优先满足用户自用特征也将直接影响投资期权价值,而据作者的文献检索发现,现有研究往往都忽视了这一问题,极少有关注。针对这一问题,本文的建模考虑了该风电站发电产出在满足自用的同时,多余电量还可出售给电网公司,并对风电自用占比变动下的投资策略进行了敏感性分析。再者,相关文献中的模型参数设定与算例分析数值多为作者主观给出,并非依据当前或历史数据统计分析得到,为此本文搜集国内外相关法规文件以及主要风电场建设项目相关数据,较为合理地估计模型参数设定。以在Ⅱ类资源区重庆某一新建社区投资新建一座分布式风电站为例说明了所提出模型与方法的基本特征。以上这几点正是本文的创新之处。综上所述,在前人研究的基础上,结合风力发电的经济性分析,对分布式风电站最优投资时机与规模等决策问题展开研究。本文的组织结构如下:第一部分说明研究方法与研究问题,并指出文章创新性与结构;第二部分构建问题的数学模型;第三部分求解与分析模型的均衡;第四部分为模型参数设定;第五部分对控制变量作了敏感性分析,最后是本文的结论。
2 模型构建
2.1问题描述与模型假设
一般地,决策者在取得分布式风电站建设权后有两种策略可供选择:即立即投资与延迟投资。两种策略的选择结果是对二者所带来收益的权衡。延迟投资相当于持有一个无到期日的看涨期权,但决策者不得不面对来自于风电价格及其发电成本的不确定性。相应地,立即投资相当于执行期权,期权的执行成本是建设与发电成本。决策者如何在这两种策略之间做出选择?其最优投资规模如何确定?继续与停止区域的边界(临界值)是什么?什么因素会影响到这种边界?这种边界是否可达、可达概率与可达时间如何?这正是下文要建模解决的主要问题。
应解决问题的建模之需,首先需做一些主要的假设:1)投资是完全不可逆的且决策可以被延迟;2)决策者的收益函数是最大化期权的净现值;3)分布式风力发电贡献毛益服从几何布朗运动;4)电站的建设是瞬时完成且立刻产生现金流;5)拥有投资权的决策者只有一种建设选择:建设分布式风电站;6)决策者无税收支出及其它各种寻租成本。
2.2基本变量及其标准化
1)电价
风电价格是影响分布式风电站投资策略选择最重要的不确定因素。考虑到在市场条件下,短期价格会有波动,但其通常是一个均值回复过程,这一般不会影响投资决策,因此在后面发展的模型中忽略了这种短期变化。长期价格漂移过程采用几何布朗运动来描述[15-16]。新的鼓励分布式风力发电的政策或机制的变化往往会导致风电价格出现跳跃现象。但作为初步的研究工作,这里暂且不予考虑。
现阶段,假设终端零售电价p1(t)以用户支付的平均电费计算,由电网公司依据综合购电平均成本及其合理收益制定;上网电价p2(t)实行政府指导价,但各省级电网公司通常采用当地火电机组脱硫标杆电价支付购电费用,若政府指导价高于标杆电价,则电网公司会享受相应的补贴。
2)投资规模
企业的投资规模大小通常表现为企业未来生产能力的高低,即通过投资所形成的项目产出规模,进而影响企业投资效益的好坏。企业增大投资规模有两个相反方向的作用:一方面增大了投资成本,实际产出数量达不到产出规模,企业生产能力将闲置,产生利润甚至不足以弥补投资成本;另一方面灵活地调整实际产出数量,享受产量增加带来的收益。因此,如何确定分布式风电站的最优投资规模将是本文研究的重点。
在所考察的时区内,设分布式风电站的投资规模用其建成后的年发电量Q(t)来衡量,单位为kW·h;发电产出不仅能满足自用(情形1),富余电量还可出售给电网公司(情形2),电能损失在此忽略不计,其中自用占比为λ,则出售占比为1-λ。
3)风力发电成本
分布式风电站的发电成本可划分为2类:与投资规模相独立的固定成本,主要包括对风电站的维护与监督管理费用。下文将此固定成本作为投资成本的一部分考虑,原因在于分布式风电站建成后,关闭不发电绝对不是最优策略,这就意味着固定成本肯定要发生;与投资规模相关的变动成本,主要包括燃料成本、设备运行维护更新费用、电网接入费、销售费用、人工费以及资金成本等,且由分布式风电自用和出售成本构成。其中,分布式风电自用成本主要是指风电机组以及风场的运行维护费用,而出售成本除包括自用成本外,还包括售电环节产生的电网接入费、电力输送与销售费用等。
4)贡献毛益
分布式风力发电站的贡献毛益主要取决于风电价格以及可变发电成本,因此本文采用此二者之间的差额来定义贡献毛益,即:
χi(t)=pi(t)-ci(t)
(1)
式中,i=1、2分别表示分布式风电自用和出售情形,ci(t)为分布式风电站的边际发电成本,χi(t)为相应的贡献毛益。由于需同时考虑风电价格及其发电成本的双重不确定性,因此本文将分布式风力发电的贡献毛益过程视作为由内、外生性因素共同发挥作用的随机过程。不失一般性,假设贡献毛益服从几何布朗运动,则[10]:
(2)
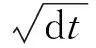
5)延迟投资机会成本
设决策者为风险中性,经过其风险调整的分布式风电站预期回报率为r,由资本资产定价(capital asset pricing model,CAPM)模型可得:
r=r0+ερσχ
(3)
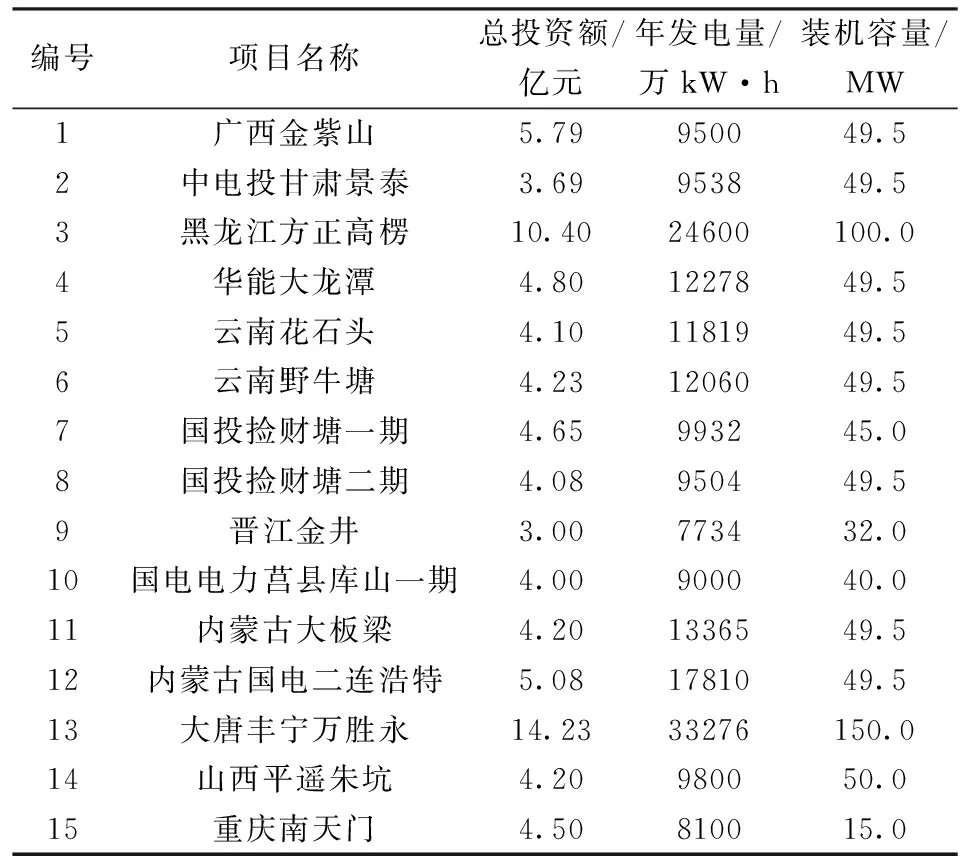
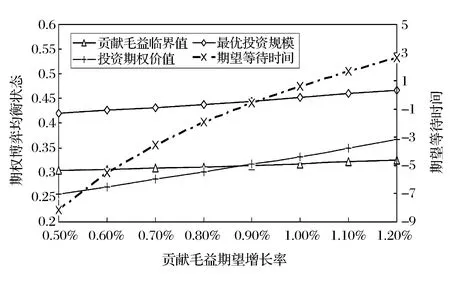
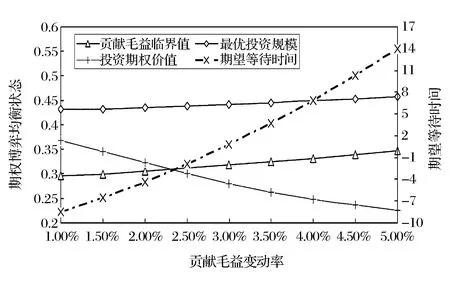
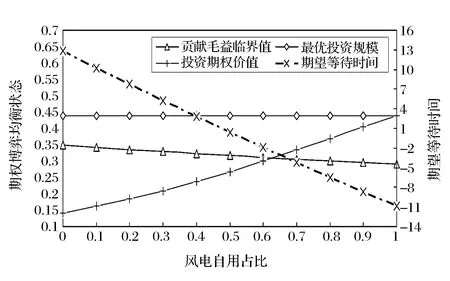
式中,r0为无风险利率;ε和ρ均为正常数,分别表示风险的市场价格和该项目收益率与市场组合收益率的相关系数。考虑到如果μχ≥r0,则延迟投资总是决策者更好的策略,从而最优解不存在,所以在此只考虑μχ 6)价值函数 与实物期权理论中假定投资无时限不同,本文考虑了分布式风电站具有投资时限的情形。事实上,分布式风力发电在中国属于新兴技术产业,项目的经济寿命往往常极为有限。在这样的背景下,投资有时限的假设更符合实际。 在有限的时区内寻求分布式风电站的最优投资策略,这就需要解析表出分布式风电站建成后的价值函数及其投资成本。下文中,首先将价值函数定义为风力发电的贡献毛益和投资规模的函数,然后将投资成本描述为投资规模的函数。 在前文的基本假设及符号说明下,可得分布式风电站的价值函数为: (4) 式中,E(·)为期望值算子,T分布式风电站的投资时限,V(·)为分布式风电站的价值函数。 7)投资成本 分布式风电站的投资成本包括风电机组、进口关税、联网和输电工程、通讯、必要的土建工程、土地征用、前期费用、管理监理费用、保险、准备费、外汇风险以及建设期利息等,且不同投资规模对应的投资成本是不同的。 已有较多文献对分布式能源项目的投资成本与规模选择之间的关系进行了研究,如Bøckman等[10]和Singal等[17]研究发现每一个小水电项目都存在一个有限的最大投资规模,且越接近该极限值,边际投资成本越大。在此基础上,进一步论证出小规模水电站的投资成本可表示为年发电量的指数函数,该研究结论与Bean等[18]和Dangl等[19]建立的投资成本模型实质上是一致的。本文采用这一研究成果,将分布式风电站投资成本定义为: I[Q(t)]=κeαQ(t) (5) 式中,κ和α为分布式风电站投资成本,且值为正的影响参数;I(·)表示分布式风电站投资成本,且是关于投资规模的凸函数。 2.3目标函数 单个分布式风电站的电能供给量有限,不具备与电网公司讨价还价的能力,因而是风电交易价格的接受者。但是一旦确定了投资规模,只要风电价格大于边际发电成本,使分布式风电站一直维持在发电状态都是有利可图的。 由式(4)可以看出,贡献毛益的随机变化导致了分布式风电站价值的不确定性,在此不确定情形下的净现值(Net present value,NPV)决策准则为: (6) 如果将投资机会视为美式看涨期权,投资决策就等同于决定何时以何种价格执行这一期权。因此,投资决策可以看做是期权定价问题,采用动态规划方法求解。 虽然求解上述最大化问题的方法有很多,如或有债权(Contingent claim)方法、动态规划方法以及最优停时方法。但是,由于该问题是一个无到期日且无终止回报(Termination payoff)的久期美式期权问题,所以下文将主要利用时间水平无穷的连续时间动态规划方法的基本方程:无即期收益(Immediate profit)的Bellman方程来解决这一问题[20]。至此,分布式风电站的实物期权定价模型可表示为: (7) 式中,F(·)表示投资时机的价值,即投资的期权价值。 在分布式风电站的投资决策过程中,有两个关键问题亟待解决:一个是应当何时投资,即投资时机问题;另一个是应当投资多少,即投资规模问题。本部分将以投资机会的期权定价模型为基础,对此两个问题依次加以解决,从而得到最优投资策略。 3.1最优投资规模 为推导分布式风电站的投资时机和投资规模,首先可求出既定外生冲击水平下的最优投资规模。给定贡献毛益初始值为χi,则根据伊藤积分,式(2)有如下解: (8) 对于任意的t值,这是一个对数正态分布随机变量,进一步求出其数学期望为: E[χi(t)]=χieμχt (9) 分布式风电生产贡献毛益的不确定性引起投资风险问题,虽然上式给出了贡献毛益的期望函数,但是在整个投资时限内,贡献毛益的即时实现值均可能会出现显著大于或小于上述期望值。另外,在式(1)中易证自用情形下的贡献毛益更大。为便于论述,假设二者之间存在正比例关系χ1(t)=ηχ2(t),其中η>1为常数。考虑到风力发电及其并网调度稳定性,在不变产出的条件下,将式(9)代入式(4)中,得: (10) 最优投资规模即受到一定的贡献毛益限制,使得NPV最大化的风力发电量。求解式(6)右端关于Q的一阶条件,得到风力发电的边际价值等于边际投资成本,进而最优投资规模为: (11) 由此不难发现,分布式风电站的最优投资规模Q*是其风电出售获得贡献毛益初始值χ2的单调递增函数。 3.2最优投资时机 (12) 由于投资机会F(χ2)在执行投资的时刻t*之前不会产生现金流,持有它的唯一回报是其资本增值,在连续时间段的Bellman方程为[7]: rF(χ2)dt=E[dF(χ2)] (13) (14) 将式(2)代入式(14),因E[dz(t)]=0时可忽略dt的高阶项,进而得到: (15) 将上述E[dF(χ2)]代入式(13)中,于是原Bellman方程可重写为: (16) 根据Dixit和Pindyck[7]标准实物期权分析方法,分布式风电站的投资期权价值形式为: (17) 式中,A1、A2为待定常数;β1>1、β2<0均为关于r、μχ以及σχ的非线性函数,且满足: (18) 由于这一一元二次方程的判别式大于0,故其必在两个相异解,且: (19) 为进一步分析,F(χ2)在必须满足的式(15)基础上,还应该满足以下三个边界条件[21]: 第一,初始零值条件,即F(0)=0,说明的是在χ2为零情形下,投资期权将不会被执行,因而该期权的价值也必须为零,此条件保证了微分方程的解具有经济学意义。这样,只取β1>1,则可以把式(17)改写成: (20) 另外两个条件来自对最优投资的考虑,以保证期权执行时不存在套利机会,同时使得期权价值不仅是连续的,而且在临界值处是平滑的。 (21) 表示执行最优投资决策时的期权价值与立即投资的净现值相等。该边界条件反映了期权执行时期权的损益。 (22) (23) 由式(22)最大化条件得到: (24) 考虑到净现值决策规则作为一个实物期权决策规则比较的基准,为此将式(11)代入(6)中,并求解其对χ2的一阶偏导数并令其等于零,解之可得: (25) (26) 随着不确定性的增大,实物期权决策规则下的最优投资临界值及分布式风电站的价值都将增大,此时决策者更愿意推迟投资。这表明不确定性增大了项目的等待价值,决策者推迟投资,并最终投资于更大的产出规模,以满足未来市场需求增长的需求,这与Dangl[19]研究结论相吻合。 将式(24)分别代入式(11)和(12)中,可得分布式风电站的最优投资时机和投资规模为: (27) 3.3贡献毛益临界值可达性 设首次到达时间(First passage time)为t*,则对于形如式(2)的随机过程,参考Rhys等[22]对实物期权执行时间(exercise time)的理论分析,随机变量t*的密度函数f(·)可表示为: (28) (29) (30) 4.1发电成本 目前,国际上比较通用的分布式风电站运行维护费用为0.05元/kW·h。在中国,可再生能源发电项目接网费用的收费标准是按线路长度制定:50 km以内为0.01元/ kW·h,50~100 km为0.02元/kW·h,100 km及以上为0.03元/kW·h[23]。分布式风力发电成本除接网费外,还涉及电力输送和销售费用等,而中国目前还没有此方面的明确规定。据欧盟2005年官方核定指导价,电力输送费用为0.25欧元/MW·h,销售费用为0.31欧元/MW·h[10]。考虑到分布式风电接入线路长短及其上网销售各有差异,不失一般性,本文在此取c1=0.05元/kW·h、c2=0.08元/kW·h。 4.2投资成本 由于缺乏实际案例数据,在此将以陆地风电场的投入产出水平近似替代分布式风电站技术水平。利用国内近年主要风电场建设项目的投资总额、年发电量以及装机容量数据(见表1),采用回归分析法估计分布式风电站的投资成本系数κ和α。 由于表1所列的风电场建设项目装机容量大多为49.5 MW,而根据发电容量的规模大小,分布式发电可分为微型:5 kW以下、小型:5 kW至5 MW、中型:5 MW至50 MW以及大型:50 MW至300 MW等4个层次,即分布式风力发电规模一般均在50 MW以下,相关数据修正后经回归拟合得到κ=4.776×107,α=2.686×10-8。 4.3风力发电贡献毛益 分布式风力发电收益主要包括自用节省支出以及出售给电网公司所获收益。自用收益与用户终端零售电价直接相关,而终端零售电价则由当地用户所属消费类型决定。以重庆市为例,取其阶梯电价执行方案的第二档标准:月用电量为200~400kW·h(含),居民生活用电价格为0.57元/kW·h,将其设为终端零售电价初始值。 表1 近年中国主要风电场建设项目相关数据 数据来源:作者根据中国风电网(http://wp.china-nengyuan.com/)发布的近年风电场建设项目相关资料整理。 出售收益主要包括向电网公司售电所得收益、补贴以及清洁发展机制(clean development mechanism,CDM)收益。在中国电网公司一般按照当地火电机组脱硫标杆价支付购电费,而火电机组脱硫标杆价往往低于风电上网指导价,差额部分享受补贴。由于在中国CDM尚不健全,且小规模分布式风电项目的CDM收益较难以实现,这里暂不考虑这部分收益。因此出售收益与上网指导电价数值相等。现阶段我国风电上网指导价为0.51、0.54、0.58以及0.61元/kW·h[24],取中间值p2=0.54元/ kW·h为初始上网电价。由此计算得到自用与出售分布式风电的贡献毛益正比例系数η=1.13。 4.4其他相关参数 分布式风电站投资时限:风电场经济生命周期一般是20~30年[25],考虑到我国风电设备制造水平相比国外仍有差距、机器设备需加速折旧,分布式风电站投资时限取T=20年。 无风险利率一般即银行的年存款利率,本文在此选取r0=5.8%;而市场风险价格与市场组合的相关系数则直接沿用Farzin等[26]的研究数据,即ε=0.4和ρ=0.7;考虑到风电自用占比因具体项目而异,对其无特别要求,故这一取值范围为0~100%。 贡献毛益期望增长率与变动率:近年风电站设备投资成本逐年下降,而土地使用费等其他固定成本却在逐年增加,且风电长期合约电价又是非公开数据,因此直接利用历史数据计算较为困难[25]。本文采用某地区火电厂年平均利润增长率以及变动率来替代,不妨假设μχ=0.8%和σχ=2.5%。 某一能源公司决定在Ⅱ类资源区重庆某一新建社区投资新建一座分布式风电站,主要用以解决该小区居民用电问题。本项目拟采用国产直驱永磁技术风电设备,预估满负荷年利用小时数约1800小时。随着小区陆续投入使用后,初步估计风电站60%的年发电量将用于自用,余下全部出售给电网公司。将上一部分中的参数设定取值代入式(11)和(24),可得此分布式风电站的出售贡献毛益临界点为0.311元/kW·h,最优投资规模为4381.3713万kW·h。如果给定该项目的初始贡献毛益为0.316元/kW·h,初始值高于临界值则表明决策者应该立刻投资,相应获得的净现值为0.3012亿元。 虽然在这一情景下的各参数取值均为常数,但是实际应用中各参数经常是变动的,因此会影响决策者的最优投资策略。本部分将对相关参数变动下的投资决策行为进行敏感性分析。 图1 贡献毛益期望增长率变动下的投资决策 图2 贡献毛益变动率变动下的投资决策 图3 风电自用占比对投资决策的影响 图4 初始贡献毛益对投资决策的影响 本文根据分布式发电的优先自用特征与风电站的经济特性,在贡献毛益增长不确定前提下,运用实物期权理论建立了分布式风电站最优投资时机与规模决策的期权定价模型。具体决策过程分为两个阶段:首先评估风电站的投资收益和成本,分别构建最优投资规模以及价值函数;然后评估推迟投资该项目的实物期权价值,求解出最优投资规模,并分析贡献毛益临界值及其可达性。最后,通过算例分析验证了研究结论并对贡献毛益期望增长率与波动率、风电自用占比以及初始贡献毛益变动下的投资决策进行了敏感性分析。 研究结果表明:对投资有时限的分布式风电站而言,贡献毛益临界值、最优投资规模、以及期望等待时间均与贡献毛益的期望增长率和变动率正相关,而延迟投资的期权价值与此二者相关性存在差异,且影响的显著性也不同;在一定条件和贡献毛益波动范围内,决策者推迟投资的期权价值与相应的期望等待时间随风电自用占比或初始贡献毛益的增大而分别增大和减小,但风电自用占比对最优投资规模,以及初始贡献毛益对贡献毛益临界值与最优投资规模都并无影响;决策者的最优投资决策需同时考虑贡献毛益临界值及其最优投资规模。 虽然本文所发展的分布式风电站实物期权定价模型具有实用价值,但是尚有一些未尽工作,如关于平均首次可达时间、可达概率与模型中各参数之间的定量与定性关系没有做详细推导,且模型假设中只有一种建设机会、无税收、无寻租成本、以及建设没有时滞等。而事实上,考虑各类成本及其波动性问题、考虑建设的时滞性问题、考虑建设机会的多样性与组合性问题都是富有意义与富有成果的研究切入点,但由于不可能在一篇文章中尽述所有,关于这些问题的探讨我们将在后续的研究中深入展开。 [1] 李俊峰,蔡丰波,唐文倩,等.中国风电发展报告2011[M].北京:中国环境科学出版社,2011. [2] 艾芊,郑志宇.分布式发电与智能电网[M].上海:上海交通大学出版社,2013. [3] Dixit A K.Irreversible investment with price ceilings[J].Journal of Political Economy,1991,99(3):541-557. [4] McDonald R L,Siegel D R.The value of waiting to invest[J].Quarterly Journal of Economics,1986,101(4):707-727. [5] Pindyck R S.Irreversibility investment,capacity choice and the value of the firm[J].American Economic Review,1988,78(5):969-985. [6] Quigg L.Empirical testing of real option-pricing models[J].Journal of Finance,1993,48(2):621-640. [7] Dixit A K,Pindyck R S.Investment under uncertainty[M].Princeton :Princeton University Press,1994. [8] 阳军,孟卫东,熊维勤.不确定条件下最优投资时机和最优投资规模决策[J].系统工程理论与实践,2012,32(4):752-759. [9] Fleten S-E,Maribu K M,Wangensteen I.Optimal investment strategies in decentralized renewable power generation under uncertainty[J].Energy,2007,32(5):803-815. [10] Bøckman T,Fleten S-E,Juliussen E,et al.Investment timing and optimal capacity choice for small hydropower projects[J].European Journal of Operational Research,2008,190(1):255-267. [11] 刘国中,文福拴,薛禹胜.计及温室气体排放限制政策不确定性的发电投资决策[J].电力系统自动化,2009,33(18):17-22,32. [12] 刘敏,吴复立.基于实物期权理论的风电投资决策[J].电力系统自动化,2009,33(21):19-23. [13] 钟渝,刘名武,马永开.基于实物期权的光伏并网发电项目成本补偿策略研究[J].中国管理科学,2010,18(3):68-74. [14] Boomsma T K,Meade N,Fleten S-E.Renewable energy investments under different support schemes:A real options approach[J].European Journal of Operational Research,2012,220(1):225-237. [15] Schwartz E S,Smith J E.Short-term variations and long-term dynamics in commodity prices[J].Management Science,2000,46(7):893-911. [16] Pindyck R S.The dynamics of commodity spot and futures markets:A primer[J].Energy Journal,2001,22(3):1-29. [17] Singal S K,Saini R P,Raghuvanshi C S.Analysis for cost estimation of low head run-of-river small hydropower schemes[J].Energy for Sustainable Development,2010,14(2):117-126. [18] Bean J C,Higle J L,Smith R L.Capacity expansion under stochastic demands[J].Operations Research,1992,40(3):210-216. [19] Dangl T.Investment and capacity choice under uncertain demand[J].European Journal of Operational Research,1999,117(3):415-428. [20] 张新华,叶泽,赖明勇.考虑价格上限的寡头发电投资阈值与容量选择[J].管理科学学报,2012,15(9):1-9. [21] Siddiqui A S,Marnay C.Distributed generation investment by a microgrid under uncertainty[J].Energy,2008,33(12):1729-17337. [22] Rhys H,Song Jihe,Jindrichovska I.The timing of real option exercise:Some recent developments[J].Engineering Economist,2002,47(4):436-450. [23] 中国国家发展和改革委员会.可再生能源电价附加收入调配暂行办法[Z].发改价格[2007]44号,2007. [24] 中国国家发展和改革委员会.关于完善风力发电上网电价政策的通知[Z].发改价格[2009]1906号,2009. [25] 张文宝,王友.风电场不同机组技术经济性的分析[J].能源技术经济,2011,23(3):46-48,58. [26] Farzin Y H, Huisman K J M,Kort P M.Optimal timing of technology adoption[J].Journal of Economics Dynamics and Control,1998,22(5):779-799. Abstract: Under the premise of contribution margin varying randomly,distributed power generation first serves self-use as well as its economic characteristics are considered.Based on the real options theory,the option pricing model for investment opportunity in distributed wind power stations is established,and the contribution margin threshold,optimal investment scale,the option value and expected waiting time of delayed investment are solved.A case study is presented to validate the main conclusions,and give the influence variation of different parameters on the equilibrium state.It is found that for distributed wind power stations with limited investment time,contribution margin threshold,optimal investment scale,and expected waiting time are all positively related to the expected increase and variation rate of contribution margin.Meanwhile,the option value of delayed investment has different correlations with these two rates,and the significances of the influences are different.In a certain condition and range of contribution margin,the option value of delayed investment and expected waiting time increases and decreases respectively,with the increase of the proportion of generated wind power for self-use or initial contribution margin.However,the proportion of generated wind power for self-use does not influence the optimal investment scale,and the initial contribution margin does not influence the contribution margin threshold and optimal investment scale.The decision-maker’s optimal decision should take both contribution margin threshold and optimal investment scale into consideration. Keywords: distributed wind power;real options;contribution margin threshold;investment threshold;expected waiting time A Study on Investment Strategies for Distributed Wind Power Stations Based on Real Options HUANGShou-jun1,YUBo2,ZHANGZong-yi2 (1.Lingnan(University)College,SuYat-sen University,Guangzhou 510275,China;2.School of Economics and Business Administration,Chongqing University,Chongqing 400030,China) TM614;F272.3 A 1003-207(2017)09-0097-10 10.16381/j.cnki.issn1003-207x.2017.09.011 2016-03-06; 2016-08-29 国家自然科学基金重点资助项目(71133007) 黄守军(1985-),男(汉族),安徽马鞍山人,中山大学岭南学院,特聘副研究员,博士,研究方向:电力经济及技术创新管理,E-mail:hsjqy@163.com.
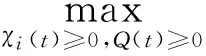
3 均衡策略求解
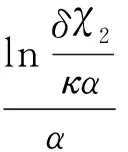

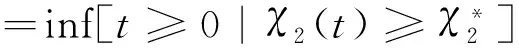
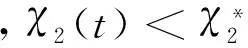
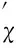
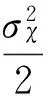
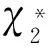
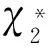
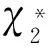
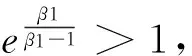
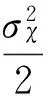
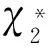
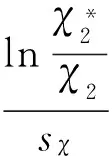
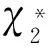
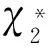

4 模型参数设定
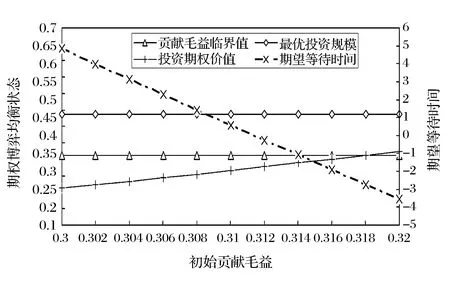
5 算例分析
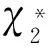
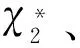
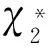
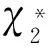

6 结语

