基于O2O的大型零售企业城市配送网络优化研究

赵泉午，赵军平，林 娅

(1.重庆大学经济与工商管理学院，重庆 400030;2.重庆大学现代物流重庆市重点实验室，重庆 400030)

基于O2O的大型零售企业城市配送网络优化研究

赵泉午1,2，赵军平1,2，林 娅2

(1.重庆大学经济与工商管理学院，重庆 400030;2.重庆大学现代物流重庆市重点实验室，重庆 400030)

本文研究了O2O转型背景下大型零售企业城市配送网络优化面临的中转中心选址及末端需求点分配问题，构建了考虑配送中心到末端需求点近似配送距离的中转中心选址及末端需求点分配联合优化模型，设计了集成遗传算法和禁忌搜索算法的混合算法求解模型，通过混合算法与CPLEX的对比证明了本文算法的有效性。以苏宁重庆主城核心区域的城市配送网络优化为实例进行测算，给出了苏宁重庆主城核心区域中转中心的选址及需求点分配的联合优化方案。联合优化方案表明城市物流“最后一公里”末端配送成本占城市物流总成本的比例超过60%；车型是影响城市物流总成本的关键因素，选择与中转中心容量接近的车型能够显著降低城市物流总成本，减少运输距离；合理的中转中心选择能提高短距离配送比例和减少配送总距离。

O2O转型；选址-分配；“最后一公里”；遗传算法；禁忌搜索算法

1 引言

布局O2O模式是国内大型零售企业应对电商对冲击的重要途径。2014年国内连锁百强有75家开展网络零售，其中23%的门店提供自提服务。门店是实施O2O的关键环节，目前国内大型零售企业的O2O转型模式分为三种。第一种是门店仅提供商品展示及消费体验服务，不涉及任何线上订单的物流功能。第二种是门店提供线上订单的物流中转服务，以少数门店作为中转中心，为周边末端需求点提供配送服务。第三种是门店在前两种模式的基础上，提供客户自提、商品包装等服务，实现了线上线下库存及服务的共享融合。目前国内大型零售企业(苏宁、国美等)O2O布局以前两种模式为主。城市内部核心区域需求密度大，需求量集中，中转中心选址关系到城市物流系统运作效率和成本，各企业纷纷优化布局城市核心区域的中转中心，完善“最后一公里”配送。

中转中心选址问题属于物流设施选址问题，大量文献进行了研究。Aikens等[1]研究了现有多种选址模型，认为模型的选择应根据问题特征而定。Shen等[2]研究了包含一个供应商，多个需求不确定零售商的选址及库存联合优化模型，建立非线性规划模型进行求解。Tsao等[3]综合考虑区域配送中心选址、需求点分配及区域配送中心库存策略使物流总成本最小，论文采用非线性规划求解。Taniguchi等[4]应用双层规划研究了公共物流站点选址问题，采用遗传算法得出最优解。Wang Yong等[5]采用遗传算法和粒子群混合算法研究了两层物流网络设施选址及分配问题，并以中国贵阳为例对算法进行检验，其设计的算法适用于优化小规模的双层物流系统。Diabat等[6]研究了单个产品多层次库存选址联合优化问题，并采用拉格朗日松弛多阶段算法进行求解。Amir等[7]研究了价格影响需求和库存容量对物流设施选址的影响，通过数据模拟得出所建模型适用于优化价格、选址和库存联合优化。Jouzdani等[8]通过构建混合整数规划模型研究了交通拥堵及需求不确定下奶制品供应链规划问题。唐金环[9-12]研究了碳排放对企业物流设施选址的影响，企业可通过设施选址、车辆选择、路径设计等方式以较小代价降低碳排放。O2O物流设施选址与B2C物流设施选址具有相似特征，针对B2C物流设施选址问题，刘必争等[13]认为B2C车辆配送业务需考虑车辆的回访特性，并建立带软时间窗的选址-路径集成模型，结合遗传算法和退火算法求解。周翔等[14]考虑顾客满意度最大和运输成本最低两个目标，对B2C模式下城市配送物流网络中末端节点数量、配送中心和末端节点的选址进行研究，构建了两阶段优化模型并求解。蒋忠中等[15]建立选址-分配模型，设计基于嵌入表上作业法的遗传算法求解。Xu Bin等[16]立足于提升物流系统效率和降低运输成本研究了B2C两级物流分拨体系，采用Lingo软件求解证明模型的有效性。Torabi等[17]研究了电商物流库存设施选址和库存转运问题，建立了混合整数规划模型，通过数据仿真说明了库存转运对于电商企业的重要性。Yu等[18]研究了引入第三方物流时考虑车辆不返回的设施选址及路径问题，采用模拟退火算法进行求解，通过算例证明算法有效性。文献[19-22]研究了模糊需求下物流设施选址问题，集成优化设施选址、分配及路径规划。

现有文献侧重优化算法设计，以随机生成中小规模算例验证算法有效性，缺乏明确应用背景，并且末端需求点规模设置鲜有超过300个。本文以苏宁等国内大型零售企业O2O转型实践为背景，综合考虑中转中心运营成本、车辆往返配送成本和车型选择等因素，构建整数规划模型对具有容量限制的城市配送中转中心选址、末端需求点分配和末端配送问题进行研究。本文的创新处体现在如下几点：一是基于苏宁等国内大型零售企业O2O转型实践为背景研究城市配送中转中心选址及末端需求点分配问题。二是针对问题特性及模型特点，论文综合了遗传算法和禁忌搜索算法的优点，基于启发式规则设计了集成混合算法，并通过混合算法与CPLEX软件求解结果的对比，验证本文混合算法的有效性。三是采用Daganzo[24]提出的距离估算方法测算中转中心到末端需求点的配送距离，该测算方法使得配送距离更加接近车辆日常配送距离。四是本文以苏宁重庆主城核心区域为实例进行测算，给出了不同情景下选址及末端需求点分配的具体方案，所得结论契合实际，具有较高的决策参考价值。

2 问题及模型

2.1问题描述

本文研究国内大型零售企业实施O2O转型面临的城市配送网络优化设计问题，也就是从城市配送中心到消费者过程中面临的中转中心选址和末端需求点分配问题，中转中心的备选地址为城市区域内全部零售门店。城市配送中心承担库存、包装、分拣、运输甚至流通加工等功能。中转中心承担订单的中转分拨功能。末端需求点包括自提点、公共快递取送点、自提柜等形态。城市配送中心到中转中心一般采用轻型卡车运输，中转中心到末端需求点采用三轮车、摩托车、面包车及电动车等车型进行配送。末端需求点同时回收客户的退换货，将退换货送至中转中心，由中转中心转送至城市配送中心。城市配送物流总成本包括从城市配送中心到中转中心的运输成本、中转中心运营成本和中转中心到末端需求点的配送成本。

2.2变量及参数定义

为方便刻画大型零售企业城市配送网络优化中面临的中转中心选址以及末端需求点分配问题，定义如下变量及参数。

I:备选中转中心集合，I={1,2,…,m}；

J:末端需求点集合，J={1,2,…,n}；

Oi:备选中转中心i每天运营固定成本；

F(·):中转中心i每天包裹处理成本，包括装卸、分拨等成本，与包裹处理量有关；

f1,f2:配送中心到中转中心、中转中心到需求点运输(配送)车辆固定成本；

c1:配送中心到中转中心货车单位距离运输成本；

di:配送中心与中转中心i之间的距离；

Mi:备选中转中心i日最大中转量；

vc1,vc2:配送中心到中转中心、中转中心到末端需求点车辆容量；

c2,c3: 中转中心到末端需求点的配送车辆每天人工成本、配送车辆单位运输成本；

rj,qj:末端需求点j平均每天配送量、退货量；

Li:中转中心i到末端需求点的配送车辆总行驶距离；

zij：当j客户需求点由中转中心i服务时为1，否则为0；

yi：是否选中备选地点i作为中转中心，选中为1，否则为0。

2.3联合优化模型

为更好构建中转中心选址及末端需求点分配的联合优化模型，本文做如下三个重要假定。

假定1：以末端需求点的日平均配送量为基准进行优化

末端需求点的配送量是变化的，本文研究侧重战略层面的中转中心选址问题，因此以末端需求点的日平均配送量为基准进行优化。每天具体配送量的变化可以在每天运作层面的路径及调度优化中实现。

假定2：中转中心到多个末端需求点配送距离采用近似算法

为了使配送距离近似测算更接近日常状况，采用连续逼近法测算配送车辆的行驶距离。Eilon[23]通过仿真得出当末端点均匀分布在正方形区域，中转中心i到所服务末端需求点的配送距离Li与所服务末端需求点个数N之间的关系可以近似表示为：

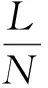
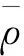
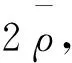
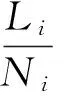
假定3：中转中心运营成本存在规模效应，采用阶梯函数刻画运营成本

F(x)表示中转中心的包裹处理费用，通常随着中转中心中转量的增长。由于存在规模效应，运营成本不能认为是简单的线性函数[20]。成本函数可表示为：

x表示i中转中心包裹处理量，Ni和Mi是中转中心的临界参数、最大中转量，Ej0为系数，θ中转中心规模效应系数，θ∈(0,1)。

基于以上三个重要假定，构建如下联合优化模型：

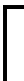
(1)

s.t.

∑izij=1,∀j∈J

(2)

∑jzijrj≤Mi,∀i∈I

(3)

rj>qj,∀j∈J

(4)

zij≤yi,∀i∈I,∀j∈J

(5)

∑jzij≥yi,∀i∈I,∀j∈J

(6)

zij,yi∈{0,1},∀i∈I,∀j∈J

(7)

式(1)为最小化物流总成本，其中包括从配送中心到中转中心运输成本，中转中心运营成本和包裹处理成本，中转中心到末端需求点的配送成本。约束条件(2)表明末端需求点有且只有一个中转中心为其提供服务，约束条件(3)表明中转中心日中转量不得大于中转中心容量，约束条件(4)表明末端需求点退换量小于需求量，保证车辆动态负载不超过其容量，约束条件(5)(6)(7)为决策变量之间的关系及变量属性。

3 模型求解

对于模型的求解，当前学者采用智能算法与启发式算法相结合的方式。国外文献方面，Tsao等[3]采用连续逼近算法求解，Wang Yong等[5]采用扩展粒子群算法与遗传算法相结合的混合算法，Diabat、Amir等[6-7,12]分别采用基于拉格朗日松弛的启发式算法和遗传算法，Torabi等[17]采用Bender分解法等。国内方面，唐金环等[9]采用基于遗传算法的细菌觅食和粒子群理论(BFA-PSO)，杨珺等[10]采用禁忌搜索算法，周翔等[14]采用基于最小生成树聚类算法，关菲等[19]采用多目标粒子群算法求解模型。本文提出了基于末端需求点配送量及配送距离的相对大小的启发式规则分配末端需求点，综合利用遗传算法、禁忌搜索算法和启发式算法的优点，设计混合优化算法对模型进行求解。

3.1遗传算法和禁忌搜索混合优化算法

本文使用遗传算法生成中转中心开放方案，充分利用遗传算法搜索范围广的特点，由于禁忌搜索算法对初始解有较强的依赖性，基于启发式规则生成末端需求点初始分配方案，采用禁忌算法优化末端需求点的分配方案。混合算法的具体步骤如下：

步骤1随机产生一定数量的选址方案作为初始种群，计算当前种群中全部开放中转中心总容量。若总容量小于末端需求点的总需求，增选任意尚未开放的备选中转中心，直到总容量大于总需求。

步骤2对种群中个体执行以下操作：

步骤2.1按3.2所示方法生成末端需求点初始分配方案。

步骤 2.2按3.3所示方法生成优化分配方案。

步骤 2.3若达到终止条件，转步骤3，否则转步骤2.2。

步骤3记录当前最优解和对应目标值。

步骤4采用适应度函数计算当前种群个体的适应度。

步骤5对种群进行选择、交叉和变异操作，并将新的最优解加入下一代种群中，同时更新种群代数。

步骤6当迭代次数大于算法设定的最大代数时，输出优化结果。否则转步骤2。

3.2基于启发式规则的初始分配算法

采用末端需求点配送量及配送距离比值由大到小的启发式规则对末端需求点进行分配：

步骤1测算开放的中转中心与末端需求点之间的距离dij。

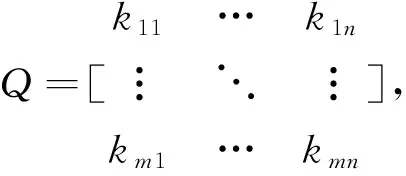
步骤3取矩阵Q中kij的最大值ki′j′，ki′j′表示末端需求点j′预分配中转中心i′，检查i′中转中心剩余容量能否满足末端需求点j.当满足时，将末端需求点j′分配给中转中心i′，同时删除该末端需求点j′所在列；当不能满足时，ki′j′点置零。

步骤4重复执行步骤3直到将全部末端需求点完全分配给中转中心，生成初始分配方案。

3.3基于禁忌搜索算法的优化分配算法

定义“移动”、“交换”两个操作。以A、B为例，“移动”指将中转中心A服务的一个或几个末端需求点改由B中转中心服务；“交换”指属于A服务的若干个末端需求与属于B服务的若干末端需求点进行交换。

应用禁忌搜索算法对分配方案进行优化，具体步骤如下：

步骤1生成选中中转中心与末端需求点距离表，1A表示中转中心A服务需求点1，如表1所示：

步骤2“移动”操作。随机选择两个选中的中转中心A和B，计算A中转中心服务的末端需求点距离B中转中心的距离，将距离最小的需求点改由B中转中心服务，判断是否满足B中转中心容量约束；若不满足容量约束，放弃当前操作；若满足执行“移动”操作。

步骤3“交换”操作。随机选择两个选中的中转中心A和B，分别计算A中转中心服务的末端需求点距离B中转中心的最近距离，以及B中转中心服务的末端需求点距离A中转中心的最近距离。交换中转中心A和B中距离对方最近需求点，同时判断末端总需求是否超过容量。若未超过，执行“交换”操作；否则放弃“交换”操作。

步骤4当候选解满足藐视准则时，用满足藐视准则的最佳状态替代当前状态成为新的当前解，并用与原状态对应的禁忌对象替换最早进入禁忌表的禁忌对象，并转步骤6；否则转步骤5。

步骤5判断候选解对应的各对象的禁忌属性，选择候选解集中非禁忌对象对应的最佳状态为新的当前解，同时用与之对应的禁忌对象替换最早进入禁忌表的禁忌对象。

步骤6判断终止条件，是则停止，否则转步骤2。

4 算法有效性分析

CPLEX是IBM开发的求解规划问题的商业软件之一。能最少用户干预、精确地解决问题，已有学者在研究解决较大规模物流与供应链问题时证明CPLEX在解决规模较小问题时具有好的求解精确度，但在求解问题规模较大时，CPLEX效率不高[27]。本文采用CPLEX求解结果作为验证混合算法求解有效性的基准。

构建一组算例验证上述模型和算法的可行性和有效性。算例的参数采用5.1实际测算参数，各项数据在对应区间范围内随机生成。表1中规模4*10指4个备选中转中心和10个末端需求点，其他情形以此类推。本文采用Matlab R14编程语言实现上述混合算法，运行平台为:

AMD,A8-7650K,Radeon,R7,10Compute Cores 4C+6G@3.3GHZ,Win8 PC。

针对问题特性，混合算法在求解模型过程中采用启发式规则进行人工干预，生成一个较优质初始解，极大提高了算法后续搜索效率。模型求解配送距离方式较为复杂， CPLEX在求解时间显著大于混合算法。混合算法执行结果与CPLEX模型求解结果相对比，两者效果相当，混合算法效率高于CPLEX，也说明了CPLEX在针对小规模问题时表现出更优异的性能，当问题规模较大情况较为复杂时混合算法表现更加优异。

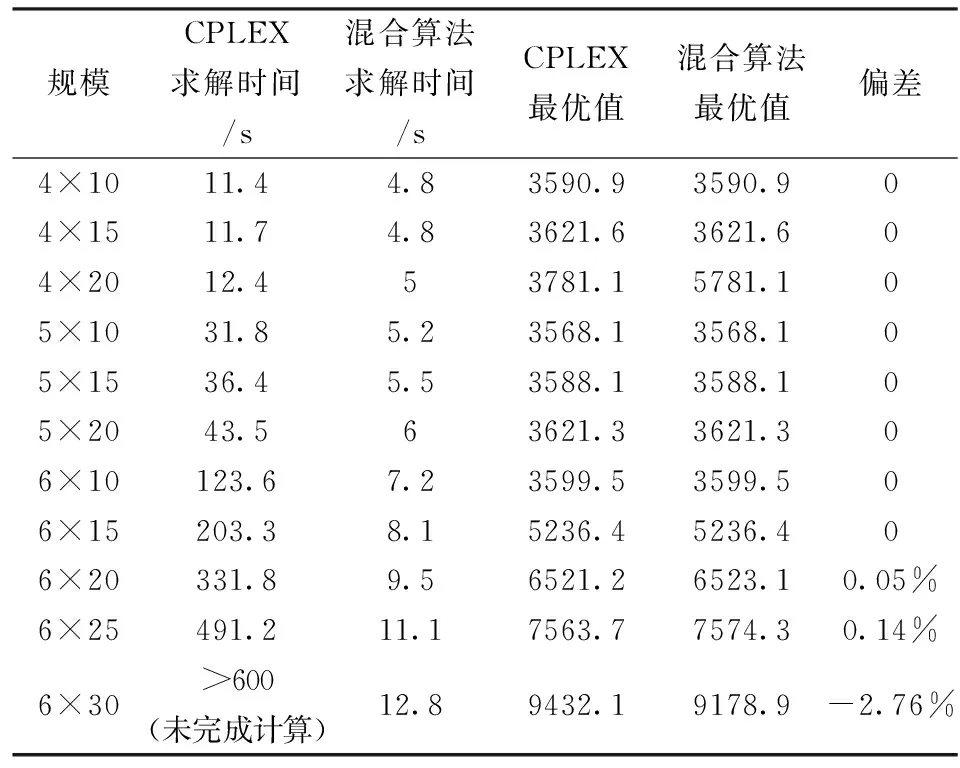
表1 CPLEX求解与混合算法性能比较

5 苏宁重庆实例分析

5.1模型测算

本文以苏宁重庆主城核心区域的城市配送网络为实例，各项数据均来源于苏宁重庆实地调研。苏宁在重庆拥有1个城市配送中心，承担线上订单的分拨转运和线下商品的库存、分拣、包装和城市配送等职能。主城核心区域15家门店(表2)，为实现线上线下城市配送的融合，在15家门店中选择若干家作为线上包裹中转中心。选中的门店作为实体门店展示销售商品的同时，承担周边一定范围内线上包裹的中转和末端需求点配送服务。本文将重庆主城核心区域15家门店作为备选中转中心，末端需求点划分根据重庆主城核心区域的人口分布、消费水平及交通状况等，将重庆主城核心区域划分为419个末端需求点，各个末端需求点的线上包裹配送需求量依据实地调研数据和经验估算。

表2 苏宁重庆主城区核心区域门店信息

从配送中心到中转中心采用直送方式，以福田欧马可1.49T厢式轻卡为例，车辆购买费用10.23万元，车辆购置税8744元，折旧年限5年，保险税5203元/年，驾驶员工资6000元/月，以此计算车辆平均行驶固定成本为272元/天，车辆行驶变动费用3元/公里(包括过桥过路费、燃油费、轮胎损耗费等)。额定载重1.49T运输车包裹输送量约1000个/车·次。中转中心配置面积50-70平方米，日处理能力800-1400个包裹，由于门店处于不同城市区域，租金略有不同，租金区间大致为每天3.5-5元/平方米，中转中心除租金外固定开支1000元/天，包括了人员工资/水电费和设备使用费等。中转中心到末端需求点的配送车辆多采用面包车或摩托车，容量平均在80个包裹，车辆固定成本与人工成本合计为210元/天，配送车辆变动成本3.5元/公里。根据前文设计的混合算法，结合相关文献参数，本文设定遗传算法种群规模100，交叉概率0.5，变异概率0.1，禁忌表长度20，禁忌搜索400，迭代次数20，对实例进行求解。将以上参数、测量数据带入模型，编程运行15次，剔除5个相同结果，得出10个不同方案(表4)。

5.2结果讨论

5.1采用车型为福田欧马可1.49T厢式轻卡，最大容纳包裹1000个，由于中转中心处理量介于800-1400之间，车型改变会对中转中心选择和末端需求点分配产生影响。本节以庆铃五十铃1.25T厢式轻卡，福田欧马可2.0T厢式轻卡为例进行测算。表3为3种车型参数对比。

表3 车型参数对比

表5是基于1.25T运输车型得出的10个中转中心开放方案，其中最大成本30548元，最小成本29290元，平均成本29878.2元，平均成本较5.1上升2.3%，平均运输距离204.83千米，增加32.7%，平均配送距离654.2千米，增加2.9%。表6是基于2.0T运输车型得出的10个中转中心开放方案，最大成本29099元，最小成本27796元，平均成本28507.2元，较5.1平均成本下降2.43%，平均运输距离139.64千米，降低9.5%，平均配送距离597.58千米，下降6.0%。由于通常状况下中转中心包裹日处理量处于800-1400，因此采用实际容量小于800车型会增加运输车数量，增加总运输距离，增加固定成本和运输成本，大于1400车型会增加车辆固定成本。

根据表3、表5和表6的中转中心选址及末端需求点分配优化方案，得出城市物流总成本中，配送中心到中转中心的运输成本、中转中心的运营成本和中转中心到末端需求点的配送成本占比分别约为6.7%、33.3%、60%。“最后一公里”末端配送成本占整个城市配送成本的60%，同时影响客户体验，是城市配送物流的关键环节。

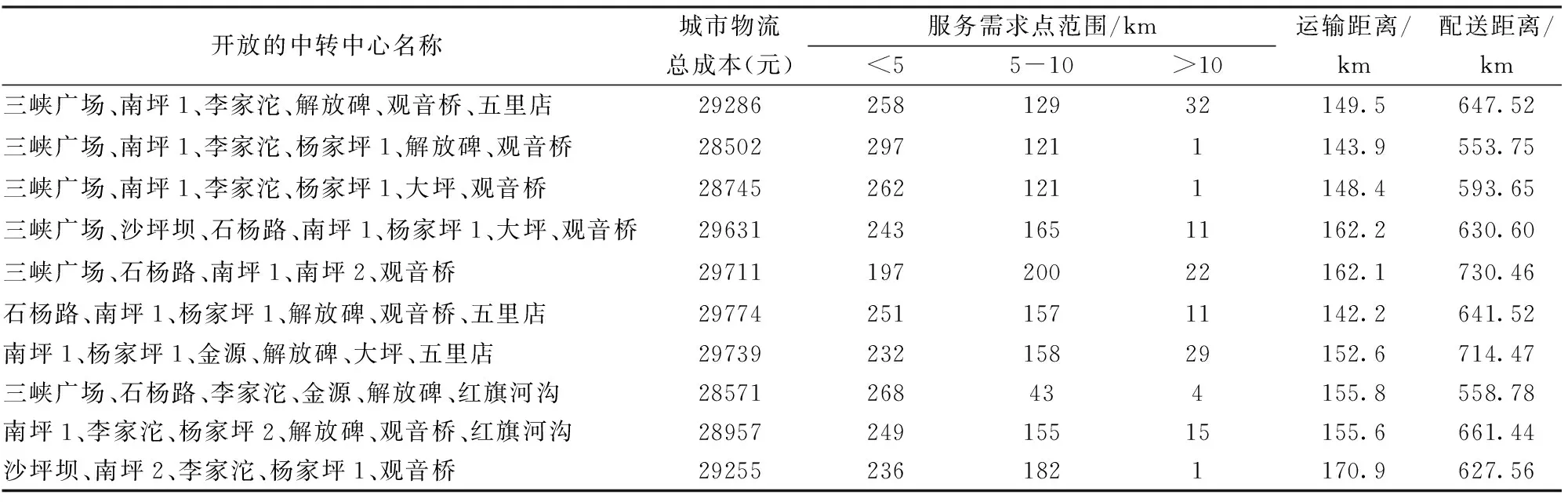
表4 中转中心开放方案

注1：南坪1对应南坪店，南坪2对应南坪江南大道店，南坪3对应南坪西路店；杨家坪1对应杨建设广场店，杨家坪2对应杨家坪店。

2：运输距离指配送中心到所有开放中转中心的总距离；配送距离是所有开放中转中心到其服务末端需求点的配送总距离。下同。

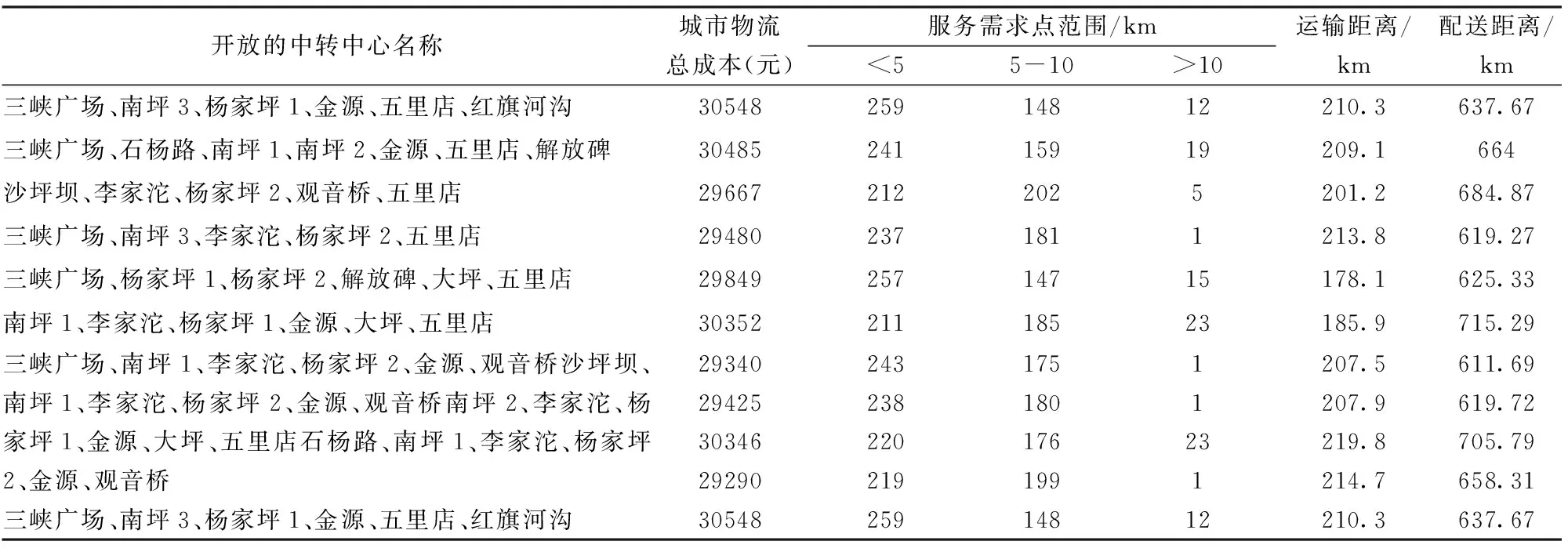
表5 基于庆铃五十铃1.25T厢式轻卡的中转中心开放方案

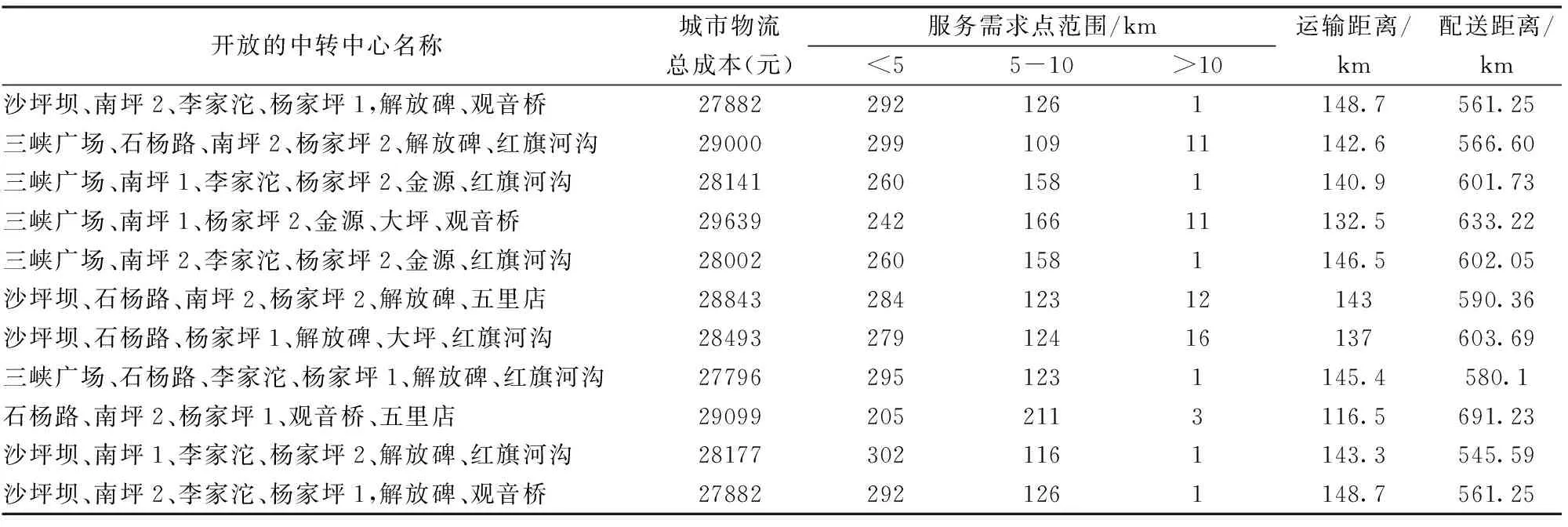
表6 基于福田欧马可2.0T厢式轻卡的中转中心开放方案

表3、表5和表6方案中，苏宁重庆主城核心区域的城市物流年总成本最大约为1150.02万元，最小约为1014.55万元。2014年苏宁重庆线上线下总营业额54亿元，主城占比约为65%，主城核心区域线上销售占比约为20%，线上物流费用占线上营业额约2.5%。主城核心区需求占主城需求量超过75%，以此计算2014年线上部分城市物流总成本约为1755万元，该项费用包含了城市配送中心的运营成本，其占比约10%，因此苏宁重庆主城核心区域城市物流总成本(不包括配送中心运营成本)约1184.6万元。本文优化最大成本、最小成本相比现有状况分别降低2.92%,14.36%。根据当前测算每单包裹从配送中心到客户的城市配送成本约为4.6元。按照当前重庆市内电商同城配送次日送达的时效要求条件下，外包物流订单一般1kg以下6元，因此对于苏宁重庆来说主城核心区域乃至主城区采用自有物流配送在提升效率的同时也有效节约成本。

6 结语

本文以苏宁等国内大型零售企业O2O转型实践为背景，对具有容量限制的城市配送中转中心选址、末端需求点分配和末端配送问题进行研究。不同于动态车辆路径问题，本文考虑城市核心区域“最后一公里”配送问题，在配送距离的估算上采用了由Daganzo[24]提出的距离估算方式。构建了中转中心选址及末端需求点分配的联合优化模型。设计了基于启发式规则的遗传算法和禁忌搜索算法的混合算法，并通过混合算法和CPLEX的对比验证本文算法的有效性。以苏宁重庆主城核心区域的O2O实践为基础，运用本文设计的算法给出了具体的中转中心选址及末端需求点分配优化方案，并给出了各个成本、运输距离和配送距离的具体数值，并与苏宁重庆主城核心区域的实际运作进行对比，结论表明在不考虑其他因素情况下，本文所得方案城市物流总成本相比现有状况最少降低2.92% ，最多降低14.36%。论文测算了三种不同车型对中转中心选址方案产生的影响，得出选择与中转中心容量接近车型能够有效降低物流成本，减少运输、配送距离。另外得出运输、运营、配送费用分别占到物流成本的比例约为6.7%，33.3%，60%等结论。城市交通限行及碳排放等问题都会对决策产生影响，考虑这些因素所得结论更具有参考价值，后续研究可以针对这些问题进行探讨。

[1] Aikens C H.Facility location models for distribution Planning[J].European Journal of Operational Research,1985,22(3):263-279.

[2] Shen Z J M,Coullard C,Daskin M S.A joint location-Inventory model[J].Transportation Science,2003,37(1):40-55.

[3] Tsao Y C,Mangotra D,Lu J C,et al.A continuous approximation approach for the integrated facility-inventory allocation problem[J].European Journal of Operational Research,2012,22(2):216-228.

[4] Taniguchi E,Noritake M,Yamada T,et al.Optimal size and location planning of public logistics terminals[J].Transportation Research,1999,35(3):207-222.

[5] Wang Yong,Ma Xiaolei,Xu Maozeng,et al.Two-echelon logistics distribution region partitioning problem based on a hybrid particle swarm optimization-genetic algorithm[J].Expert Systems with Applications,2015,42(12):5019-5031.

[6] Diabat A,Battaïa O,Nazzal D.An improved Lagrangian relaxation-based heuristic for a joint location-inventory problem[J].Computers &Operations Research,2015,61:170-178.

[7] Ahmadi-Javid A,Hoseinpour P.A Location-inventory-pricing model in a supply chain distribution network with price-sensitive demands and inventory-capacity constraints[J].Transportation Research Part E:Logistics and Transportation Review,2015,82:238-255.

[8] Jouzdani J,Sadjadi S J,Fathian M.Dynamic dairy facility location and supply chain planning under traffic congestion and demand uncertainty: A case of Tehran[J].Applied Mathematical Modeling,2013,37(18-19) :8467-8483.

[9] 唐金环,戢守峰,朱宝琳.考虑碳配额差值的选址-路径-库存集成问题优化模型与算法[J].中国管理科学,2014,22(9):114-122.

[10] 杨珺,卢巍.低碳政策下多容量等级选址与配送问题研究[J].中国管理科学,2014,22(5):51-60.

[11] 赵泉午,杨茜.考虑CO2排放量的城市专业物流中心选址研究[J].中国管理科学,2014,22(7):124-130.

[12] Diabat A,Al-Salem M.An integrated supply chain problem with environmental considerations[J].International Journal of Production Economics,2015,164:330-338.

[13] 刘必争,毛超.电子商务下的配送中心选址问题及其优化[J].系统工程,2008,26(10):17-20.

[14] 周翔,许茂增,吕奇光.B2C模式下配送中心与末端节点的两阶段布局优化模型[J].计算机集成制造系统,2014,20(12):3140-3149.

[15] 蒋忠中,汪定伟.B2C电子商务中配送中心选址问题及其优化[J].控制与决策,2005,20(10):1125-1128.

[16] Xu Bin,Wei Chunli,Shi Zhanjiang,et al.Study on location-selection of B2C e-commerce logistics distribution center[C]//Proceedings of 2009 International Forum on Computer Science-Technology and Applications,Chongqing,China,December 25-27,2009.

[17] Torabi S A,Hassini E,Jeihoonian M.Fulfillment source allocation,inventory transshipment,and customer order transfer in e-tailing[J].Transportation Research Part E:Logistics and Transportation Review,2015,79:128-144.

[18] Yu V F,Lin S Y.A simulated annealing heuristic for the open location-routing problem[J].Computers &Industrial Engineering,2015,62：184-196.

[19] 关菲,张强.模糊多目标物流配送中心选址模型及其求解算法[J].中国管理科学,2013,21(S1):57-62.

[20] Lau H C W,Jiang Zhongzhong,Ip W H,et al.A credibility-based fuzzy location model with Huriwicz criteria for the desingn of distribution systems in B2C e-commerce[J].Computers &Industrial Engineering,2010,59:873-886.

[21] 张晓楠,范厚明,李剑锋.B2C物流配送网络双目标模糊选址模型与算法[J].系统工程理论与实践,2015,35(5):1202-1213.

[22] Nadizadeh A,Nasab HH.Solving the dynamic capacitated location-routing problem with fuzzy demands by hybrid heuristic algorithm[J].European Journal of Operational Research,2014,238(2):458-470.

[23] Eilon S,Waston-Gandy C D T,Christofides N.Distribution management: Mathematical modelling and practical analysis [M].New York:Hafner,1971.

[24] Daganzo C F.The distance traveled to visit N points with a maximum of C stops per vehicle: An Analytic Model and an Application [J].Transportation Science,1984,18(4):331-350.

[25] Figliozzi M A.Planning approximations to the average length of vehicles routing problems with varying customer demands and routing constraints [J].Transportation Research Record: Journal of the Transportation Research Board,2008,2089:1-8.

[26] Davis B A,Figliozzi M A.A methodology to evaluate the competitiveness of electric delivery trucks[J].Transportation Research Part E:Logistics and Transportation Review,2013 49:8-23.

[27] 周愉峰,马祖军,王恪铭.应急物资储备库的可靠性P-中位选址模型[J].管理评论,2015,27(5):198-208.

Abstract： In this article,joint location-assignment problem is studied for designing an Urban Logistics Network (ULN) with multiple intermediate depots (IDs) and terminals of ULN.The key decisions are where to locate the intermediate depots (IDs) and how to assign terminals to IDs such that the total network cost is minimized.A large-scale static and deterministic integer programming model is presented solving a joint location-assignment problem of large chain retailers.To solve this model,a more efficient hybrid algorithm integrated with Genetic algorithm and Tabu search algorithm is put forward based on heuristic searching criteria.Our methodology is illustrated with the Urban Logistics Network from a leading Chinese retailer (Suning) in Chongqing.Numerical analysis suggests that optimal solutions can reduce the total network cost between 2.92%～14.36% by comparison with the current ULN .Delivery costs of “Last Mile” account for total urban logistics network costs more than 60%.Vehicle type is a deterministic factor to total urban logistics network costs.The effects of changing parameter values on the optimal solutions are also studied and some management implications are pointed out.

Keywords： online-offline channel integration;iocation-assignment problem;“last mile ";Genetic algorithm;tabu search algorithm

A City Logistics Network Optimization Model for Large Chain Retailers under Online-Offline Channel Integration

ZHAOQuan-wu1,2,ZHAOJun-ping1,2，LINYa2

(School of Economics and Business Administration,Chongqing University,Chongqing 400030,China;Chongqing Key Laboratory of Logistics,Chongqing University,Chongqing 400030,China)

U121;O221

A

1003-207(2017)09-0159-09

10.16381/j.cnki.issn1003-207x.2017.09.018

2016-01-29；

2016-10-14

重庆市社会科学规划一般项目(2015YBGL109)；国家自然科学基金资助项目(71002070)；国家社会科学基金重点项目(14AGL023)；国家科技支撑计划资助项目(2015BAH46F01)

赵泉午(1976-)，男(汉族)，河南方城人，重庆大学经济与工商管理学院教授，博士，研究方向：现代物流与供应链管理、营销渠道及零售管理，E-mail:zhaoquanwu@126.com.