半参数可加beta回归模型及其应用

方匡南，姚紫薇

(1.厦门大学经济学院，福建 厦门 361005；2.上海财经大学国际工商管理学院，上海 200433)

半参数可加beta回归模型及其应用

方匡南1，姚紫薇2

(1.厦门大学经济学院，福建 厦门 361005；2.上海财经大学国际工商管理学院，上海 200433)

当响应变量为连续比例数据时,即其取值为(0,1)区间时,经典的线性回归或者数据变换方法的结果往往不理想。这种情况下可以使用Ferrari and Cribari-Neto提出的beta回归模型。但是传统的beta回归模型仅局限于参数线性回归,模型的灵活度不高。本文提出了半参数可加beta回归模型以及参数估计方法，通过模拟发现具有良好的效果。另外，将半参数可加beta回归应用于医疗支出占家庭总支出比例的实证分析上,探讨了影响医疗支出占家庭总支出比例的影响因素。

半参数；beta回归； 广义可加模型；医疗支出

1 引言

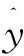
Beta回归假定连续性响应变量y服从beta分布，且取值范围为(0,1)。Beta分布的密度函数的形式多样，密度函数也随着分布参数的改变呈现出多种形态，如左偏、右偏、U型等，所以可以解决数据不对称性问题。又因为y的方差是随着beta分布的参数的变化而变化，所以beta回归可以适用于数据存在异方差的情形。

关于beta回归的研究起步相对较晚，最早由Ferrari和Cribari-Neto[1]提出了beta回归的具体模型以及参数估计方法。随后，相关的研究逐渐展开，但目前大多数都是根据Ferrari和Cribari-Neto[1]所设定的原始模型进行改进和衍生。Branscum等[2]将先验信息纳入分析，利用Markov Chain Monte Carlo (MCMC)算法，构造贝叶斯beta回归来检测时间和地理距离两个因素对引起手足口病的细菌的进化方向的影响。由于最原始的beta回归利用的极大似然估计的结果存在二阶偏差，所以模型不够准确，为此多位学者对此进行研究并提出了校正的方法和公式，比较有代表性的有Ospina等[3](2006)，Simas等[4]和Ospina和Ferrari[5]等，其中Simas等[4]还通过放宽beta回归线性的设定并使精度参数为非恒定的，增加了模型的灵活性。Cook等[6]提出了膨胀beta回归，允许响应变量出现0或者1。Pereira等[7-8]研究了截断膨胀beta回归模型，允许响应变量为子集[c,1]。此外，还有部分学者研究了beta回归模型的诊断问题，如Espinheira等[9]，Chien[10]和Anholeto[11]。

Beta回归模型本质上可以看作是一种具有参数形式的广义线性回归模型。参数模型需要对模型作一定的假设，当假设成立时，其推断有较高的精度，但当假设不成立时，参数模型所作的预测和推断效果很差。由于经济社会系统的复杂性，对模型作线性假设往往是不合理的。半参数回归模型是参数回归和非参数的回归的结合，兼具参数回归和非参数回归的优点，具有较大的灵活性和适应性。

本文在Ferrari和Cribari-Neto[1]的beta线性回归模型和Hastie和Tibshirani[12]的广义可加模型(Generalized Additive Model)基础上，结合了beta回归和广义可加模型的特点，克服了传统beta回归无法拟合非参数模型和半参数模型的缺点，提出了半参数可加beta回归模型，并研究了其参数估计方法，并将该方法应用到我国医疗支出占家庭总支出比例的影响因素分析。

2 半参数可加beta回归

本文提出的半参数可加beta回归模型的设定如下:

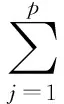
(4)

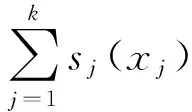
半参数可加beta回归模型求解使用的是由迭代重加权最小二乘法 (Iteratively-reweighted least-squares，IRLS)和backfitting过程合并而成的局部积分算法(Local-Scoring Procedure)，其中外部的Fisher积分过程用于链接函数的估计，而内部的backfitting过程用于估计光滑可加项。模型的估计最主要的三部分：函数sj(·)的估计，链接函数的估计以及平滑参数的选择。

2.1平滑参数的选择

平滑参数的选择是半参数可加beta回归模型估计的一个重要部分，本文主要利用的是三次样条平滑方法结合惩罚最小二乘估计方法进行拟合。三次平滑样条的形式为:

(5)

式(5)的第一项是损失函数，即最小二乘法的残差平方和，第二项是惩罚项。λ是一个非负的平滑参数，主要通过对数据的分析，综合考虑模型的拟合度和平滑度来选择其具体数值，λ越大，平滑效果越明显。一般可以依据PSE(Average Predictive Square Error)，CV(Cross-Validation)，GCV(Generalized Cross-Validation)，AIC (Akaike information criterion)来选择λ，其中最常用的是GCV和AIC(邵臻等[13])。本文采用的是AIC准则。

2.2平滑项的估计

半参数可加beta回归模型的平滑项的估计主要依据局部积分算法内部的backfitting算法计算得到。为了便于迭代，模型估计采用调整后的响应变量。令y=η(x)+ε，当已知关于η(x)的部分估计量时，可以建立以下调整后的响应变量:

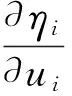
(6)

在back-fitting算法中，假设模型的形式是：

(7)

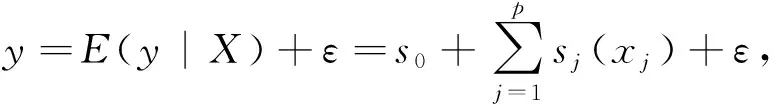
(8)

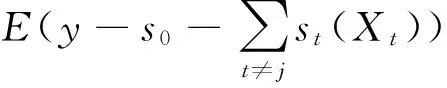
(1)初始值:

其中，g(·)为链接函数，N是样本数，m是迭代过程的循环指标。

(2)迭代：m=m+1，

ui(m-1)=g-1(ηi(m-1))

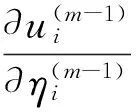
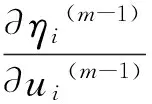
其中，vi=Var(Yi)，wi表示权重

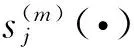
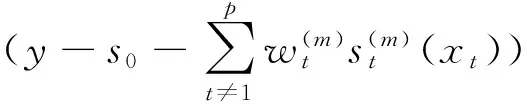
(4)重复第(2)-(3)步，直到Δ(η(m),η(m-1))足够小而收敛。

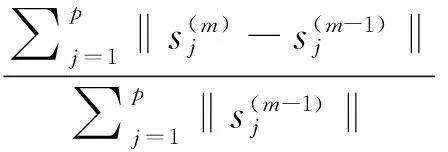
其中，ξ是事先设定的迭代容忍度。

2.3链接函数的估计

在局部积分算法中主要利用外部的Fisher积分过程用于链接函数的估计。在具体的估计过程中，首先需要预先给定η(x)的初始估计，然后通过泰勒一阶展开式并结合Fisher积分方法获得改进的估计。其中，ηgiven(x)表示η(x)的初始估计，ηest(x)表示改进后的估计。

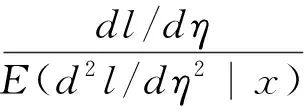
利用平滑方法来求解，则：

ηest(x)=smoother[ηgiven(x)-

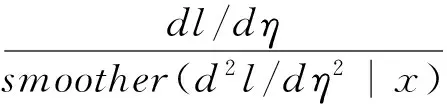
对于beta分布的极大似然函数为:

其中，

li(ui,φ)=logΓ(φ)-logΓ(uiφ)-logΓ((1-ui)φ)+(uiφ-1)logyi+{(1-ui)φ-1}log(1-yi) 一般来说链接函数会取logit的形式，即：

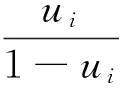
则可以根据l(u,φ)和η(x)的形式求得改进后的η(x)，即ηest(x)，然后进行进一步迭代，算出每个ηi(x)。

3 蒙特卡罗模拟

为了检验本文提出的半参数可加beta回归模型的估计效果，利用蒙特卡罗模拟方法进行分析。

模拟1：设φ=500，p=4，即考虑4个自变量，且假设每个自变量均是(0,1)上均匀分布随机数，即xj～U(0,1)，j=0,1,2,3。按式(4)生成半参数可加beta回归模型：

η=g(u)=s0(x0)+s1(x1)+s2(x2)+s3(x3)

(9)

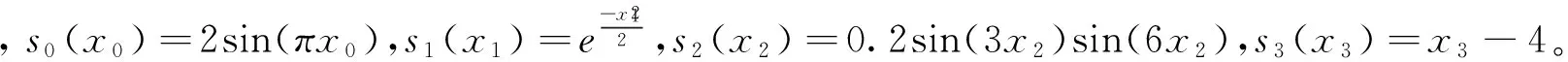
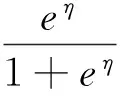
利用半参数可加beta回归模型对以上生成的数据进行拟合。回归结果显示，所有自变量都是显著的，其Null Deviance 为7.1312，Residual Deviance为0.198，Null Deviance是只有常数项的模型的偏差值，Residual Deviance是模型拟合后的残差偏差值，说明拟合的模型解释了y的大部分变动。模型的拟合结果见图2，图2中的散点是按照上文对应的函数形式所生成的随机数，实线是通过半参数可加beta回归模型拟合的回归线。从图2中可以看出，模型的拟合效果非常好，可以很好地拟合出数据的形状和弯曲走向。

接下来，利用上述模拟方式进行模拟100次，通过绘制该100次模拟的拟合图来检验模型的稳健性(见图3)。可以从100次模型的拟合图中看出，半参数可加beta的拟合效果非常稳健，平滑项的变化趋势与模拟数据的实际函数形式非常接近，对于非线性关系的数据的拟合能力非常强。此外，我们还与其他方法进行了比较，分别计算每个模型的样本内MSE和样本外MSE，详见表1。从表1可以看出，半参数beta回归模型的结果是最好的，且半参数模型结果都好于线性的参数模型结果，这个结果是很自然的，因为真实模型的假设都是非线性的函数，此时线性的参数模型存在设定误差，很难准确拟合数据，而半参数模型可以从数据本身出发，很好地拟合数据。而不管参数模型还是半参数模型，beta回归都是好于普通的线性回归，因为对于取值在(0,1)的因变量，普通线性回归的拟合值往往会超出这个范围，而beta回归可以很好拟合这个比例因变量数据。

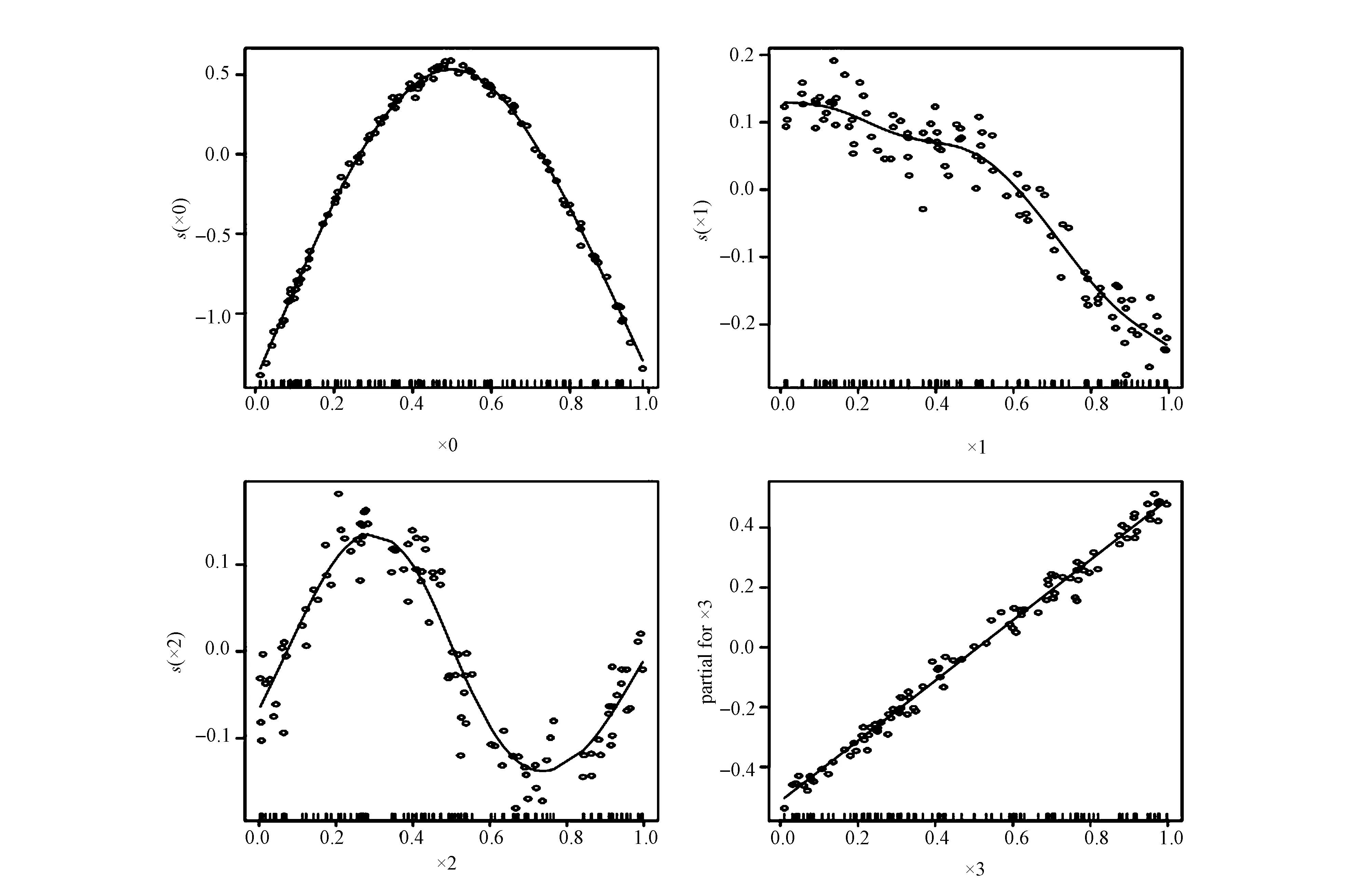
图2 半参数beta回归模型估计结果

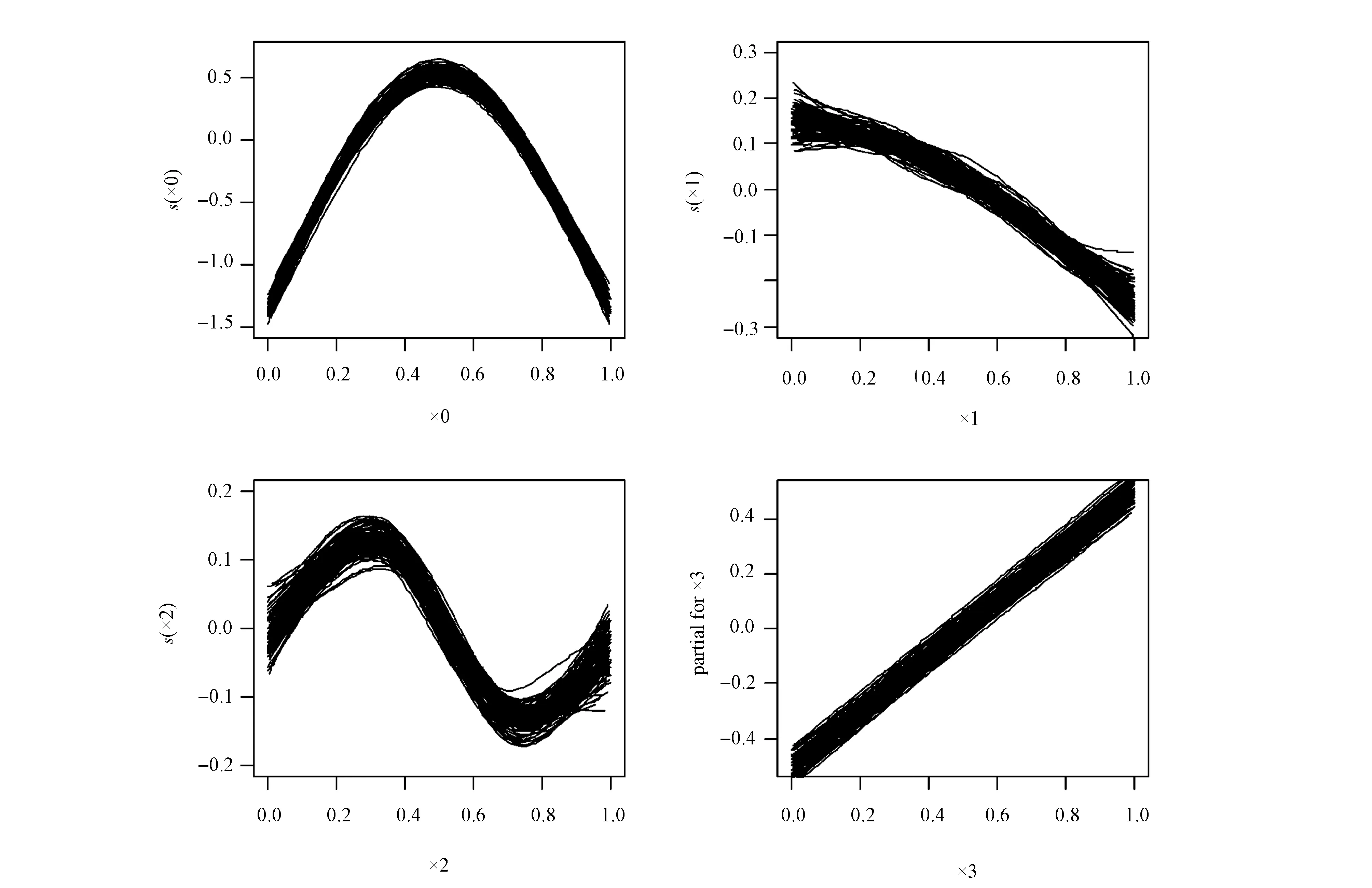
图3 100次模拟结果

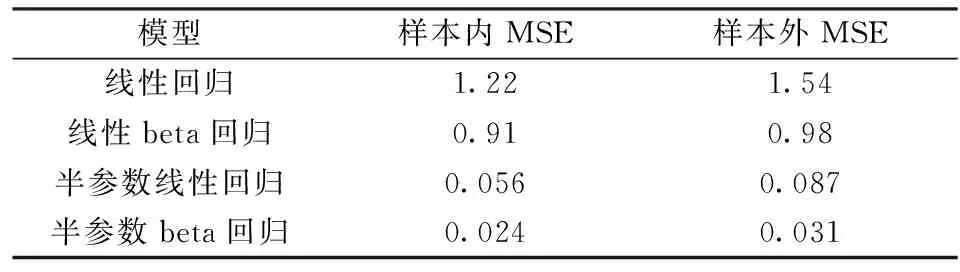
表1 模拟1的结果

模拟2：为了进一步检验模型的稳健性，我们更改模型的函数形式以及随机数的分布。设φ=1000，考虑4个自变量，假设x0仍然是(0，1)上的均匀分布随机数，即x0～U(0,1)，x1,x2是标准正态分布随机数的绝对值，即取值范围为(0,∞)，该假设和下文的实证分析中很多变量的取值范围一致，x3是二点分布随机数，即x3～binom(1,0.5)，是离散变量。按式(4)生成半参数可加beta回归模型：

η=g(u)=s0(x0)+s1(x1)+s2(x2)+s3(x3)

(10)

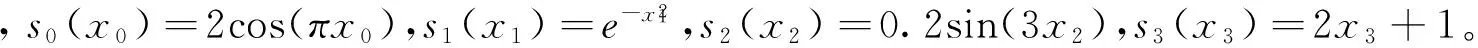
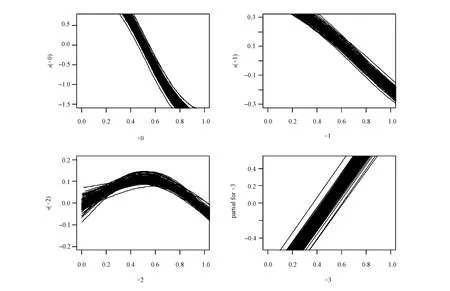
图4 100次模拟结果

4 医疗支出比例实证分析

近年来我国城乡居民医疗支出不断上涨，医疗支出成为家庭消费的重要组成部分，“看病难”“看病贵”的现象日益增多。Fang 等[14]认为医疗支出是很多家庭的一项重要支出，当家庭的医疗支出增加，会影响家庭的总消费支出及消费结构。Smith[15]研究表明，负面的健康冲击与家庭用于医疗的现金支出有直接的关联，同时也会对收入和消费产生影响。Himmelstein等[16]发现，美国的个人破产有接近一半是因为遭遇了健康困境。对于发达国家的公民，一般都有较好的健康保险，但健康的冲击仍然会对家庭的消费行为产生如此的影响。对于发展中国家而言，健康冲击所产生的负面效应应更加明显。Dercon和Krishan[17]发现，在埃塞尔比亚，家庭遭遇健康冲击时，妇女的消费会下降。Gertler和Gruber[18]对印度尼西亚的研究，也得出了类似的结论。为了防止农民因病致贫，因病返贫，2003年我国卫生部提出了在农村实施新型农村合作医疗保险制度(简称“新农合”)。理论上，新型农村合作医疗保险作为农村居民应对突发大额医疗支出的保障措施之一，在很大程度上可以减少农村居民面对的未来医疗支出的不确定性(齐良书[19]；曲卫华等[20])。本文利用入户实地调查的数据研究实施新农合后的农村居民医疗支出占家庭总支出比例的变化情况及其影响因素。

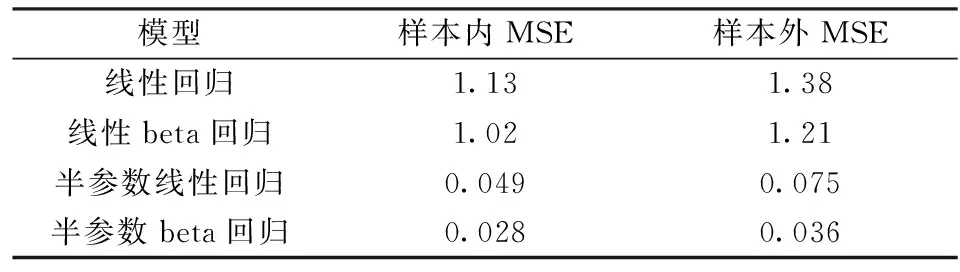
表2 模型比较

数据来源于新型农村合作医疗制度的入户调查，该项调查由美国耶鲁大学公共卫生学院、辅仁大学管理学院、厦门大学数据挖掘研究中心共同发起，具体入户调查由厦门大学数据挖掘研究中心相关研究人员完成。调查范围为福建漳州、三明、南平、龙岩、福州五个市的农村地区，调查时间为2012年7月至9月份。除去部分无效的样本，最终得到724个有效样本。各变量的说明情况请详见表3。

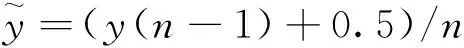
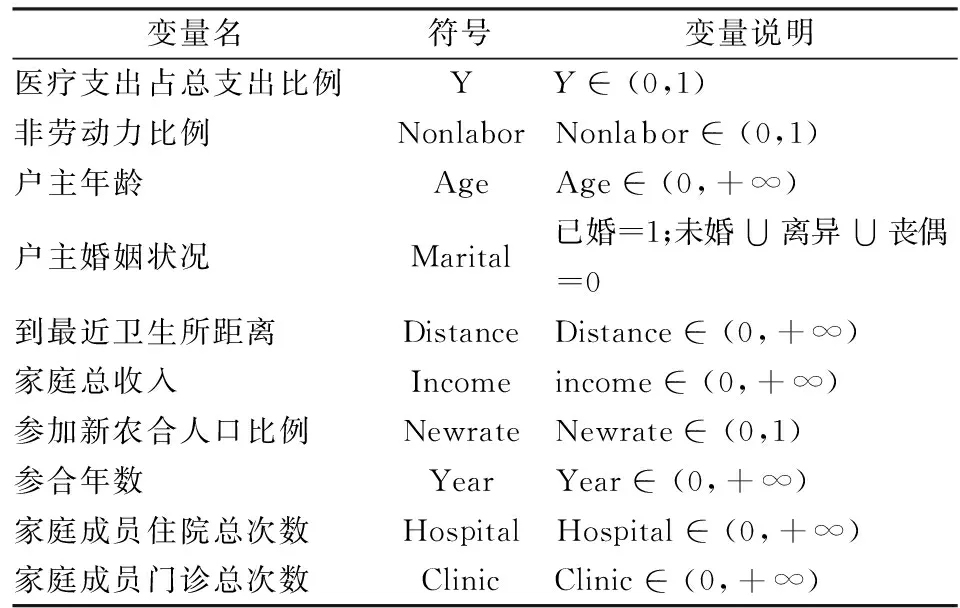
表3 变量说明

注：其中非劳动力比例是指家庭中16岁以下和65岁以上人口占总人口的比例；参合年数是指参合家庭自第一次参合距今年数。户主婚姻状况里将未婚、离异和丧偶的归为一类，已婚的归为一类。家庭成员住院总次数是指过去一年家庭所有成员到医院住院的次数总和，家庭成员门诊总次数是指过去一年家庭所有成员到医院看门诊的次数总和。

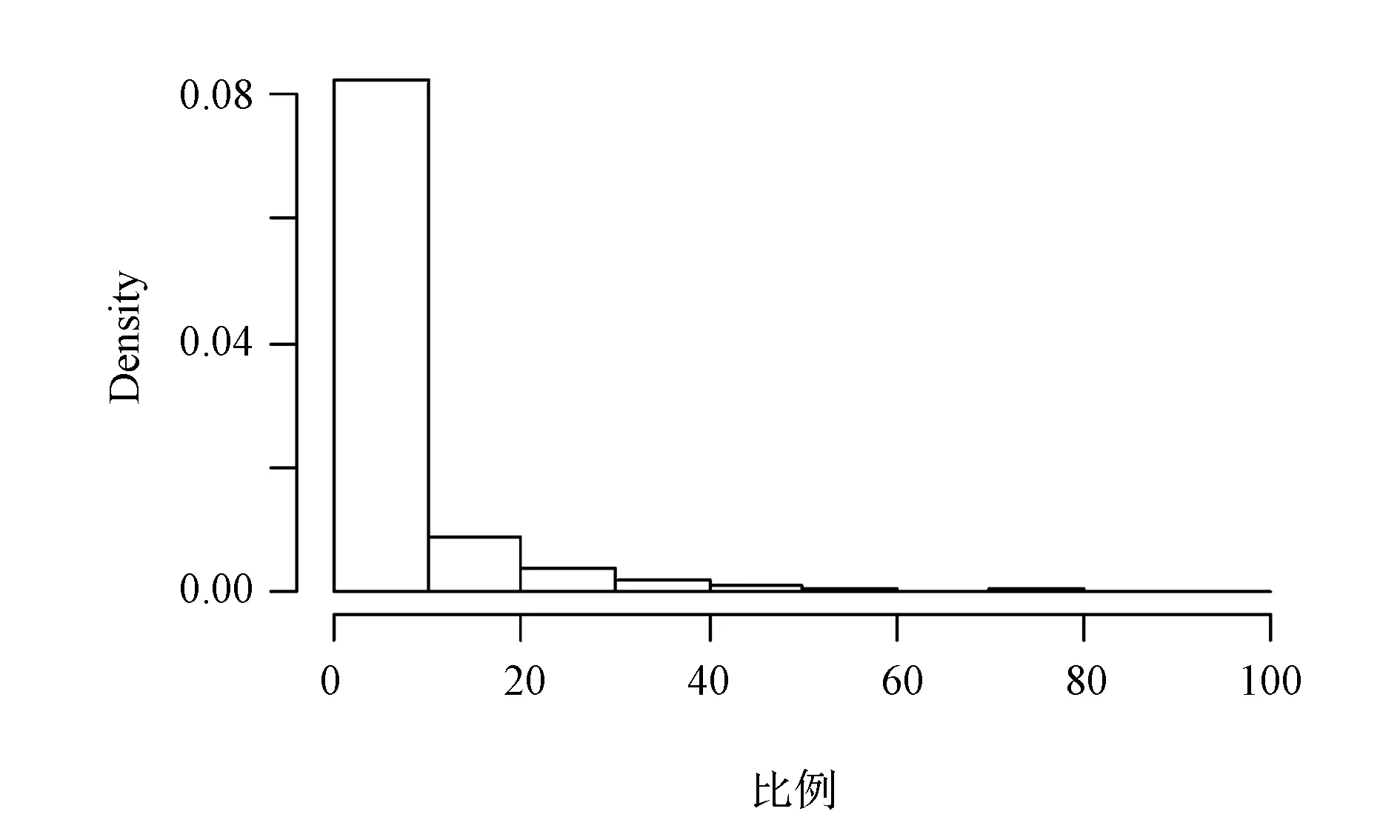
图5 医疗支出比例的分布

下面利用本文提出的半参数可加beta回归模型进行分析，响应变量为家庭医疗支出占总支出的比例。自变量为表3中其他的变量。通过拟合半参数可加beta回归，探讨农村家庭医疗支出比例的影响因素，发现最终显著的变量为户主年龄(age)、户主婚姻状况(marital)、庭总收入(income)、家庭成员住院总次数(hospital)、家庭成员门诊总次数(clinic)，其中户主婚姻状况是离散的虚拟变量，在模型中假设其线性的，而户主年龄、庭总收入、家庭成员住院次数和家庭成员门诊次数假设具有非线性特征。模型的形式为

g(u)=βmarital+s(age)+s(income)+s(hospital)+s(clinic)

(10)

对于非参数函数，我们采用三次平滑样条去展开，利用AIC选择最优的平滑参数，最终模型的AIC为-3.47。模型估计的参数部分系数为β=-0.423，说明户主的婚姻状况对医疗支出比例有显著影响，户主已婚的家庭比户主单身(未婚、离异或丧偶)的医疗支出比例要低。模型非参数部分的拟合图见图6。

从图6中可以看出，医疗支出比例与户主年龄存在正向关系，随着户主年龄的增加，家庭医疗支出比例也随之增加，但不完全是线性关系，而是存在翘尾现象，即当户主年龄超过60岁以后，家庭医疗支出比例会较快地上升。这是因为根据医学理论，当户主年龄超过60岁后，意味着家庭年龄结构偏向老龄化，发生疾病的概率大幅上升，因此，医疗支出比例也会更快地增长。

从图6可以看出，家庭总收入与医疗支出比例呈负向关系，但是并不是严格的线性负向关系。当家庭年总收入小于15万时，曲线较为陡峭，即随着家庭年总收入的增加，医疗支出比例较快下降。当家庭年总收入大于15万时，曲线变得较为平坦，即医疗支出比例下降速度减慢。这可能是由于中低收入群体的医疗花费大多是基础医疗支出，对医疗需求层次较低，随着家庭收入的增加，医疗支出比例不断下降。而对于高收入群体，生活压力相对较小，故在满足家庭基本消费之后其逐渐增加对健康的重视，对医疗需求的层次也较高，比如生病时去更好的医院以及预防保健的支出等，其医疗支出绝对值随着收入增加而增加。因此，对于高收入群体，虽然医疗支出比例随着收入的增加而降低，但其降低速度也变得平缓。

从图6可以看出，家庭医疗支出比例和家庭成员住院总次数呈折线形正向关系，即当过去一年家庭成员住院总次数从0到2次时，医疗支出比例呈较快上升，当超过2次时，家庭医疗支出比例增长变得平缓。这可能是对于住院次数超过2次的家庭，更重视参加医疗保险，包括新农合甚至其他商业医疗保险，医疗保险可以覆盖其较大部分的医疗支出。从图6可以看出，家庭医疗支出比例和家庭成员门诊总次数呈波浪形关系，当过去一年家庭成员门诊总数小于10次时，随着门诊次数的增加，医疗支出比例也增加；当门诊总次数在10次到40次之间，随着门诊次数的增加，医疗支出比例保持在一定的水平，可能是对于门诊次数在10次到40次之间的家庭，其医疗保险的意识更强，购买更多的医疗保险，可以覆盖其较大部分的医疗支出；而当门诊次数超过40次，随着门诊次数的增加，医疗支出比例也增加，这可能因为家庭即使购买了医疗保险，但医疗保险不能覆盖部分，即其自付部分的医疗支出也随之增加，因此，其医疗支出比例也增加。

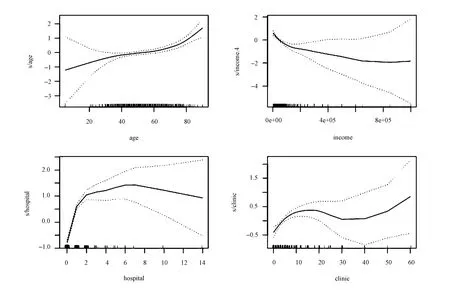
图6 医疗支出比例的回归结果 注：图中的虚线为95%的置信区间。

5 结语

在回归分析中，若响应变量为比例的连续数据，即其取值范围为(0,1)区间时，数据往往存在异方差，利用经典的线性回归模型或者数据变换后的回归模型进行预测研究时常常都不尽如人意。这种情况下可以使用由Ferrari和Cribari-Neto[1]提出的beta回归模型。但传统的线性beta回归缺少对非参数回归形式的支持。本文根据Hastie和Tibshirani[12]所提出的广义可加模型的理论框架，结合beta回归模型的特性，构建了半参数可加beta回归模型，并对模型平滑参数的选择、单变量函数sj(·)的估计以及链接函数的估计进行了研究。利用三次样条平滑方法结合惩罚最小二乘估计方法并结合AIC对平滑参数进行选择。单变量函数sj(·)的估计主要依据局部积分算法结合back-fitting算法通过重复迭代得到估计结果。而链接函数的估计主要通过在初始的η(x)基础上，通过泰勒一阶展开式并结合Fisher积分方法获得改进的估计。本文通过模拟发现，半参数可加beta回归模型的拟合效果较好。

本文利用半参数可加beta回归模型探讨了家庭医疗支出比例的影响因素。研究结果表明：户主的婚姻状况对医疗支出比例有显著影响，户主已婚的家庭比户主单身(未婚、离异或丧偶)的医疗支出比例要低；医疗支出比例与户主年龄存在正向关系，随着户主年龄的增加，家庭医疗支出比例也随之增加，但不完全是线性关系，而是存在翘尾现象；家庭总收入与医疗支出比例呈负向关系，但是并不是严格的线性负向关系。当家庭年总收入小于15万时，曲线较为陡峭，当家庭年总收入大于15万时，曲线变得较为平坦；家庭医疗支出比例和家庭成员住院总次数呈折线形正向关系，即当过去一年家庭成员住院总次数从0到2次时，医疗支出比例呈较快上升，当超过2次时，家庭医疗支出比例增长变得平缓；家庭医疗支出比例和家庭成员门诊总次数呈波浪形关系，当过去一年家庭成员门诊总数小于10次时，随着门诊次数的增加，医疗支出比例也增加，当门诊总次数在10次到40次之间，随着门诊次数的增加，医疗支出比例保持在一定的水平，而当门诊次数超过40次，随着门诊次数的增加，医疗支出比例也增加。

[1] Ferrari S,Cribari-Neto F.Beta regression for modelling rates and proportions [J].Journal of Applied Statistics,2004,31(7):799-815.

[2] Branscum A J,Johnson W O,Thurmond M C.Bayesian beta regression: Applications to household expenditure data and genetic distance between foot-and-mouth disease viruses [J].Australian &New Zealand Journal of Statistics,2007,49(3):287-301.

[3] Ospina R,Cribari-Neto F,Vasconcellos K L P.Improved point and interval estimation for a beta regression model [J].Computational Statistics &Data Analysis,2006,51(2):960-981.

[4] Simas A B,Barreto-Souza W,Rocha A V.Improved estimators for a general class of beta regression models [J].Computational Statistics &Data Analysis,2010,54(2):348- 366.

[5] Ospina R,Ferrari S.A general class of zero-or-one inflated beta regression models[J].Computational Statistics and Data Analysis,2012,56(6):1609-1623.

[6] Cook D O,Kieschnick R,Mccullogh B D.Regression analysis of proportions in finance with self-selection[J].Journal of empirical finance,2008,15 (5):860-867.

[7] Pereira G H A,Botter D A,Sandoval M C.The truncated inflated beta distribution[J].Communications in Statistics-Theory and Methods,2012,41(5): 907-919.

[8] Pereira T L,Cribari-Neto F.Detecting model misspeciflcation in inflated beta regressions[J].Communications in Statistics-Simulation and Computation,2014,43(3): 631-656.

[9] Espinheira P L,Ferrari S L P,Cribari-Neto F.Influence diagnostics in beta regression[J].Computational Statistics and Data Analysis,2008,52(9):4417-4431.

[10] Chien L C.Diagnostic plots in beta-regression models[J].Journal of Applied Statistics,2011,38(8):1607-1622.

[11] Anholeto T,Sandoval D A,Botter D A.Adjusted pearson residuals in beta regression models[J].Journal of Statistical Computation and Simulation,2014,84(5):999-1014.

[12] Hastie T,Tibshirani R.Generalized additive models [J].Statistical Science,1986,3(1):297-310.

[13] 邵臻,杨善林,高飞,等.基于可变区间权重的中期用电量半参数预测模型[J].中国管理科学，2015,23(3)：123-129.

[14] Fang Kuangnan,Jiang Yefei,Shia B,et al.Impact of illness and medical expenditure on household consumptions: A survey in western China[J].PLoS ONE.2012,7(12):1-8.

[15] Smith J P.Healthy bodies and thick wallets: The dual relation between health and economics status[J].Journal of Economic Perspectives,1999,13(2):145-166.

[16] HimmelsteinD U,Warren E,Thorne D,et al.Market watch: Illness and injury as contributors to bankruptcy[J].Health Affairs,2006,25 (5):84-88.

[17] DerconS,Krishnan P.In sickness and in health: Risk sharing within households in rural ethipoia[J].Journal of Political Economy,2000,108(4):688-724.

[18] Gertler P,Gruber J.Insuring consumption against illness[J].American Economic Review,2002,92(1):51-76.

[19] 齐良书.新型农村合作医疗的减贫、增收和再分配效果研究[J].数量经济技术经济研究，2011,(8):35-52.

[20] 曲卫华，颜志军.环境污染、经济增长与医疗卫生服务对公共健康的影响分析——基于中国省际面板数据的研究[J].中国管理科学，2015,23(7)：166-176.

Abstract： In regression analysis,classical linear regression or its transformation methods are not satisfied when response variable is restricted to the interval (0,1),that is ,proportional or fractional data,which is common in Economics,education,medical science etc.One of the most promising approaches is the beta regression proposed by Ferrari and Cribari-Neto.However,the traditional beta regression is confined in the linear situation and thus lacks flexibility.Besides,it has specification error if the true model is not linear.Borrow the idea from generalized additive model (GAM) proposed by Hastie and Tibshirani,a semi-parametric additive beta regression model is proposed.It is assumed the model can be decomposed into parametric and nonparametric parts.For the nonparametric part,the local scoring algorithm is used to fit the unknown function and AIC is used to choose the best smoothing (tuning) parameters.Two simulation examples under different scenarios are conducted,the simulation results shows that semi-parametric beta regression model perform well.Comparing to traditional models,the proposed semi-parametric beta regression model is the best and is significantly better than other traditional models.The proposed model is applied on medical expenditure data to explore the factors of the medical expenditure portion in patients’ overall expenditure.It is found marital status,age of householder,income,the number of inpatient and outpatient are the significant factor for the proportion of medical expenditure in overall expenditure.

Keywords： semi-parametric;beta regression;generalized additive models;medical expenditure

Semi-parametric Additive Beta Regression Model with its Application

FANGKuang-nan1,YAOZi-wei2

(1.The School of Economics,Xiamen University,Xiamen 361005,China;2.International College of Business Administration,Shanghai University of Finance and Economcics,Shanghai 200433,China)

F064.1；F063.4

A

1003-207(2017)09-0116-09

10.16381/j.cnki.issn1003-207x.2017.09.013

2016-06-16；

2016-12-07

国家自然科学基金资助项目(71471152，71303200)；全国统计科学研究重点项目(2015629)

方匡南(1983-)，男(汉族)，浙江台州人，厦门大学经济学院统计系教授，研究方向：数据挖掘机器学习、应用统计，E-mail:39863401@qq.com.