可抗噪声的Canny改进边缘检测算法①
徐德明, 万长林
可抗噪声的Canny改进边缘检测算法①
徐德明, 万长林
(惠州学院电子科学系, 惠州 516015)
由于图像噪声的存在, 传统的边缘检测算法常常无法准确检测到边缘信息. 本文分析了噪声条件下边缘信息的几何特征, 提出一种基于几何边缘增强技术的边缘检测算法. 首先采用Canny算子计算图像的初始边缘信息, 然后根据初始边缘信息自动计算阈值排除弱边缘, 对剩余边缘计算带方向梯度值进行增强, 根据增强边缘信息自动计算双阈值, 最后用双阈值方法检测、过滤并连接边缘. 该算法提高了边缘检测的准确性, 可以高效率地处理噪声和纹理导致的虚假边缘.
边缘检测; 图像噪声; Canny算子; 高斯滤波; 几何特征
1 引言
边缘检测是图像处理和计算机视觉中的基本问题, 边缘检测的目的是标识数字图像中属性发生显著变化的点[1,2]. 图像属性中的显著变化通常反映了图像属性的重要事件和变化, 常常体现在亮度的变化上. 这些属性变化包括: 深度上的不连续、表面方向不连续、物体纹理变化和场景照明变化. 边缘信息的检测属于高级的计算机视觉的基础. 计算机视觉以数字图像处理与识别为基础的结合人工智能、系统学等学科的研究方向, 其研究成果被广泛应用在各种工业及探测机器人上[3]. 现在已有很多边缘检测算法被提出来, 大部分算法是基于数值差分方法[4], 比如Sobel、Robert、Laplacian算子. 除了传统的数值差分类算法, 现代边缘检测技术在差分的计算方式上提出了各种改进, 比如Daniel等人[5]提出用Krawtchouk多项式近似计算差分以提高检测速度. 除了差分类方法, 还其它一些采用不同技术的算法, 比如采用蚁群优化技术[6]和神经网络技术[7]. 现代图像识别技术的一个不足就是自适应性能差, 一旦目标图像被较强的噪声污染或是目标图像有较大残缺往往就得不出理想的结果. Canny于1986年提出边缘检测算子[8]应满足以下三条准则:
(1) 较高的信噪比, 使非边缘点被误判为边缘点或者边缘点被误判为非边缘点的概率要低, 即输出的信噪比达到最大;
(2) 边缘定位准确, 即检测出的图像边缘点要尽可能在图像实际边缘的中心;
(3) 单边响应准则, 即要保证单个边缘只有一个像素响应, 并且使虚假边缘的响应在最大程度上得到抑制.
同时Canny提出了一种满足以上3条准则的边缘检测算法, 称为Canny算子, 与传统的微分算子相比, Canny 算子应用于检测图像边缘时具有运算速度快和检测精度高的优点, 因而在实践中Canny 算子被广泛应用. 但该算法存在两个主要问题: 如Canny算子采用在2×2 邻域内求有限差分均值的方法来计算梯度幅值, 虽然对边缘定位准确, 但容易被噪声干扰; 如Canny算法的双阈值都是固定的, 高低门限依赖人工设置, 自动化程度较低.
在随后的时间里, 许多针对Canny算子的改进算法[9-12]被提出来, 运算复杂问题普遍存在于这些对Canny算子的改进算法当中. 比如Arbelaez等人于2010年提出的globalPb算法一定程度上克服了Canny算子的主要问题. 抗噪声能力强, 无需人工设置阈值, 检测效果更好. 其主要步骤如下:
(1) 以不同尺度分别计算带方向的梯度值(,,)并根据多尺度组合公式

计算多尺度综合的梯度值, 其中为尺度数,为图像信息种类数(颜色、灰度、纹理).
(2) 对图像的梯度值进行“局部非极大抑制”得到边缘信息.
(3) 用谱聚类方法对图像的边缘信息进行聚类排除噪声或纹理导致的虚假边缘.
但是, globalPb算法有两个主要的问题: 运算过程复杂, 不但要对多尺度多信息计算梯度, 还需要额外的谱聚类计算排除虚假边缘; 如由于算法需要提供额外的纹理信息, 限制了它无法在缺乏纹理信息的场景中应用.
2 边缘噪声的几何特征
Canny算子在处理椒盐噪声时相对困难, 本文就以椒盐噪声条件下的边缘信息进行分析. 我们知道由于噪声会在图像中形成小范围的亮度显著变化的点(密集的纹理也有类似的特点), 采用Canny算子对亮度求导得梯度值, 并寻找局部最大梯度值时, 就会把噪声周围的点误认为强边缘. 图1是对图像加椒盐噪声后用Canny算子得到的强边缘图.

图1 噪声条件下Canny算子得到的强边缘图
如图1所示, 除了真实的强边缘, 还有许多噪声和纹理引起的虚假强边缘. 对两种强边缘进行分析后可知, 虚假强边缘尺度较小, 而且在其尺度上呈现为曲线组成的无规则图形, 而真实的强边缘在同样的尺度上往往呈现为直线, 虽然其组成的整体(大尺度)上可能是曲线. 基于这样的分析, 本文将给出一种新的几何增强的边缘检测方法, 该方法通过判断用Canny算子得到的强边缘在小尺度上接近直线的程度来估算其真假程度, 从而增强真实边缘, 削弱虚假边缘, 最终通过双阈值方法排除噪声和纹理导致的虚假边缘.
3 线性边缘增强技术
以一个边缘点周围一定大小的正方形为窗口, 考虑过该边缘点的边缘线的线性程度, 如图2所示.
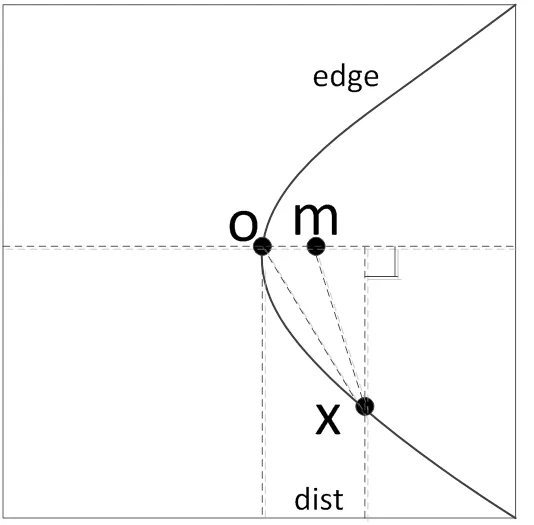
图2 Web信息抽取流程
图2中点为边缘线edge的偏移中心(质心), 如果edge越接近直线, 那么edge上的点, 例如点, 到直线om的投影距离就越短, 而在edge已知的情况下,点位置和edge上的点到om的投影距离都是可以计算得到的. 其中点坐标可以通过在o点坐标上加上一个偏移值得到, 该偏移值为edge所有点的横向梯度和与纵向梯度和, 根据算出的om坐标, edge上任意边缘点的投影距离dist可根据余弦定理求出. 然后, 该部分边缘的直线接近程度就可以通过统计所有边缘点的投影距离来计算: 将|dist|<0.5的点作为中间点, 将|dist|>=1的点作为周围点, 中间点数和周围点数的差值就可以用来作为边缘接近直线程度的数量度量, 该度量即可用于对边缘进行增强.
4 改进的Canny边缘检测算法
基于前面的分析, 本文提出一种几何增强的边缘检测算法, 该算法主要思想是: 首先用Canny算子和双阈值方法得到图像的边缘图, 然后对边缘图中的每个边缘点, 指定一个局部窗口, 在窗口中以几何方法计算以该边缘点为中心的一段边缘线接近直线的程度, 将直线接近程度作为该边缘点的增强量与原始边缘图融合, 在新的边缘图中采用双阈值方法得到强边缘和弱边缘, 从强边缘中过滤长度小于一定值的虚假边缘, 然后将强边缘和弱边缘连接得到最终的边缘信息图. 算法主要流程如图3所示.

图3 算法流程图
根据算法主要思想和流程图, 该算法可用MATLAB或C语言进行编程实现, 现将算法实现详细步骤列举如下:
(3) 对梯度图应用非极大值抑制得到边缘信息图E,非极大值抑制实质上是找到梯度图(边缘强度图)数据中的最高点,利用边缘方向信息来处理,验证所有点是否峰值,以一个3×3大小的数据区域为例,如果一个点两侧的梯度小于该点上的梯度,那么它为极大值.
(4) 对边缘信息图中的数据按数值由小到大进行排序,取排在全部数值70%处的数值大小的30%作为最低阈值,从边缘信息图中排除小于最低阈值的边缘得到边缘信息图1.
(5) 按以下步骤对边缘信息图1计算带方向梯度值的增强边缘3:
① 如图2所示,以窗口大小(默认取值为7)对边缘信息图E1中每个非零边缘点(,)计算梯度偏移位置(,),

② 计算边缘图1中每个窗口中心位置(,)与其梯度偏移位置(,)的距离的平方

③ 对窗口中每个非零边缘点(,)分别计算其到窗口中心位置和梯度偏移位置的距离的平方
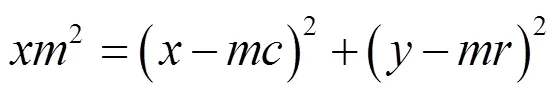
④ 根据余弦定理计算窗口中每个非零边缘点(,)到中心位置o在直线om上的投影距离
⑤ 按以下步骤对窗口的中心点(,)计算其边缘增强值2:
= 0,1 = 0,2 = 0;
循环对窗口W中的每个非零边缘点进行统计;
如果小于0.5>>-0.5, 那么=+ 1;
如果>1, 那么1 =1 + 1;
如果<-1, 那么2 =2 + 1;
如果=2, 那么2(,) = -
否则2(,) =–1 –2
⑥ 将边缘增强图2的值归一化到0-1,与边缘图1叠加并归一化到0-1,按如下公式得到边缘增强图3:

(6) 按以下步骤根据边缘信息图1和3计算双阈值:
① 将边缘增强图3中的非零点由小到大排序;
② 取排在序列中位的值作为上阈值,等于3中非零点数量减去1中非零点数量的30%,
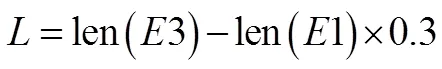
③ 取排在序列中Lx0.7位的值作为下阈值.
(7) 按以下步骤对增强的边缘信息采用双阈值方法检测并连接边缘:
① 对大于上阈值的强边缘进行过滤,滤除边缘长度小于(的优选值为8),的虚假强边缘;
② 将过滤后的强边缘与大于下阈值的弱边缘进行连接得到最终的边缘信息.
在算法中有一些参数取值值得注意, 其中计算边缘增强图时选取的窗口大小, 判断一条边缘是否直线所需的最小长度为3, 考虑计算直线逼近程度的准确性,需取一个较大值, 考虑到计算时间开销需取一个较小值, 结合实验数据本算法选取窗口大小为7; 在第6.2步计算边缘上阈值的计算公式参考了Canny算法计算上下阈值的思想, 在噪声条件下, 由于噪声的影响E3的强度偏向于向上部集中, 所以选取的上阈值也要提高; 而在无噪声条件下, 选取的上阈值偏低, 而原始边缘1 点的数量通常随噪声的增强而增加, 所以实际的上阈值可选取为3去除1的因子, 其中系数0.3的选择来自于实验数据和经验公式, 同样, 下阈值系数0.7也参考了Canny下阈值选取的思想, 结合了实验数据和经验公式.
5 实验结果
为了评估本文所提出的图像边缘检测方法的检测效果, 本文在一台配置2.5GHz双核CPU, 4GB内存的PC机上进行了对比实验, 实验图片4(a)为MATLAB 2012a软件附带的cameraman.tiff, 图片大小为256×256像素, 分辨率为72dpi. 以图4(a)的无噪声的图片作为原始图片分别采用Canny算法和本文的图像边缘检测方法进行处理, 分别得到如图4(b)和图4(c)所示的边缘信息图. 从图4.b和图4.c的对比可以看到, 采用本文的图像边缘处理方法相对于采用Canny算法可以显著提高图像的边缘检测准确性, 能够排除草地纹理导致的虚假边缘.
为了更进一步评估本文所提出的图像边缘检测方法在噪声条件下的检测效果, 以图4(a)的无噪声的图片加入噪声密度为2%的椒盐噪声的图5(a)作为原始图片, 然后分别采用Canny算法和本文的图像边缘检测方法对图5(a)进行处理, 分别得到如图5(b)和图5(c)所示的边缘信息图. 从图5.b和图5.c的对比可以看到, 即使在有噪声干扰的条件下, 采用本文提出的图像边缘处理方法相对于只采用Canny算法可以显著提高图像的边缘检测抗噪声能力.

(a) 原始图 (b) Canny算法 (c) 本文
为了评估本文所提出的方法的时间效能, 本文分别对不同大小的图片用Canny算法和本文提出的方法进行处理, 统计各自发费的时间, 以此评估算法的执行效率. 实验所采用的图片分别为MATLAB 2012a软件附带的256×256像素的cameraman.tif, 512×384像素的peppers.png, 640×480像素的fabric.png, 1200×1500像素的saturn.png, 2956×2215像素的concordorthophoto.png. 实验结果如表1所示.
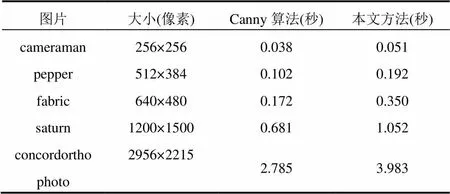
表1 算法执行效率对比实验结果
从表1可以看出, 本文提出的方法相比Canny算法运算时间只有小幅的增加, 而边缘检测效果有明显提升, 在大部分情况下性能都能满足实际应用的要求.
6 结语
本文对噪声条件下的边缘特征进行了分析, 总结出局部线性程度是衡量边缘真假的重要指标, 并给出了一种计算直线近似程度的几何方法, 在此基础上, 提出了一种几何增强的边缘检测算法, 该算法可以较准确的定位图像的边缘, 能够有效抑制噪声和纹理导致的虚假边缘, 可以自适应地改变边缘检测的高低阀值, 在增加少量计算的前提下提高了边缘检测效果和自动化程度. 最后, 对比实验的结果也验证了算法的有效性. 该算法在生产自动化的视觉检测上得到应用, 用于跟踪生产线上的工件, 自动上下料, 并进行表面缺陷检测, 取得了较好的应用效果.
1 Nixon MS, Aguado AS. 特征提取与图像处理.北京:电子工业出版社,2010.
2 Bhardwaja S, Mittalb A. A survey on various edge detector techniques. Procedia Technology, 2012, 4: 220–226.
3 盛遵冰.机器视觉图像检测与定位系统关键技术研究[博士学位论文].哈尔滨:哈尔滨工业大学,2009.
4 Fan L, Song F, Jutamulia S. Edge detection with large depth of focus using differential Haar-Gaussian wavelet transform. Opt. Commun, 2007, 270(2): 169–175.
5 Rivero-Castillo D, Pijeira H, Assunçao P. Edge detection based on Krawtchouk polynomials. Journal of Compu- tational and Applied Mathematics, 2015, 284: 244–250.
6 Liu X, Fang S. A convenient and robust edge detection method based on ant colony optimization. Optics Communications, 2015, 353: 147–157.
7 Li H, Liao X, Li C, et al. Edge detection of noisy images based on cellular neural networks. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(9): 3746–3759.
8 Canny J. A computational approach to edge detection. IEEE Trans. Pattern Analysis and Machine Intelligence, 1986, 8(6): 679–698.
9 Arbelaez P, Maire M, Fowlkes C, Malik J. Contour detection and hierarchical image segmentation. IEEE TPAMI, 2010, 33(5): 898–916.
10 Hao F, Shi JF, Zhang ZS, Chen RW, Zhu SQ. Canny edge detection enhancement by general auto-regression model and bi-dimensional maximum conditional entropy. Optik, 2014, 125(15): 3946–3953.
11 Li HQ, Liao XF, Li CD, Huang HY, Li CJ. Edge detection of noisy images based on cellular neural networks. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(9): 3746–3759.
12 殷海青,江玲玲,刘红卫.联合纹理提取和边缘检测的新方法.系统工程与电子技术,2010,32(4):846–850.
Noise-Proof Enhanced Canny Edge Detection Algorithm
XU De-Ming, WAN Chang-Lin
(Department of Electronic Science, Huizhou University, Huizhou 516015, China)
Because of the existence of image noises, classical edge detection operators often fail to detect the edge exactly in many cases. In view of this, we analyze the geometry characters of edge under the condition of noises, and propose an enhanced algorithm of Canny operator, based on geometry edge enhancing. The algorithm firstly applies Canny operator to compute initial edges, and then excludes weak edges according to an automated threshold. In the following, it computes the directed gradients of remaining edges to improve the edges, and computes the double thresholds according to the improved edges. Finally, this algorithm detects filters and connects the edges by the double-thresholds method. This algorithm improves the accuracy of the edge detection, and can handle the false edges caused by noises or textures efficiently.
edge detection; image noise; Canny operator; Gauss filter; geometric feature
科技部科技型中小企业技术创新基金项目(14C26214402603);惠州学院教博启动项目(2015JB015)
2016-04-29;收到修改稿时间:2016-06-12
[10.15888/j.cnki.csa.005581]

