一种改进的Inter-Apriori算法①

崔双弥, 张德生



一种改进的Inter-Apriori算法①

崔双弥, 张德生

(西安理工大学理学院, 西安 710054)

建立了一种基于定位和权值事务项集的挖掘算法, 该算法只需扫描一遍事务数据库. 利用垂直型布尔矩阵来存储交易数据, 通过 “与”运算与权值来计算计算支持度, 利用定位搜索和合并事务矩阵相同列来剪枝, 从而减少了算法在挖掘过程中使用的存储空间和计算时间. 实验结果表明, 改进算法在性能上得到了的明显提高.

频繁项集; 垂直型布尔矩阵; Inter-Apriori算法

1 引言

关联规则挖掘[1]是数据挖掘领域的一个重要问题, 旨在发现大量数据中项集之间有趣的关联或相关联系. 这些关联关系可以为商业决策者提供有价值的信息, 从而实现商务决策的制定, 如交叉销售、商品摆放等.

Apriori算法[2]是挖掘关联规则最经典的算法, 它在执行“连接-剪枝”的过程中采用逐层搜索的迭代方法来挖掘满足阈值的关联规则, 但存在两个缺陷: (1)重复多次扫描事务数据库; (2)产生的候选集数据过大.

近年来, 基于矩阵的关联规则挖掘算法研究快速发展, 使得挖掘效率进一步提高. 如基于压缩矩阵的研究方法[3,4]、基于矩阵分解的研究方法[5]、基于上三角矩阵的研究方法[6]、基于排序索引矩阵的研究方法[7],基于矩阵和数组的研究方法[9,10]等,文献[11]提出了基于矩阵取交集的Inter-Apriori算法, 但当Tidset的规模庞大时将出现以下问题: (1)求Tidset的交集的操作将消耗大量时间,影响了算法的效率; (2)Tidset的规模相当庞大, 消耗系统大量的内存. 文献[12]提出对项集矩阵进行累加运算, 虽能大大提高挖掘效率, 但只适用于事务数据库中, 重复事务多的情形. 文献[13]提出了基于散列布尔矩阵的研究方法, 虽然大大减少了算法的比较次数, 提高了算法效率, 但却增加了算法的空间复杂度, 加大了开销.

针对以上问题, 本文建立了一种基于垂直型布尔矩阵的挖掘关联规则频繁项目的算法, 该算法将事务数据库映射为垂直型布尔矩阵, 在此基础上进行挖掘频繁项集, 很大程度上减少了时间和空间消耗.

2 Inter-Apriori算法的改进

2.1 建立垂直型布尔矩阵

定义1. 项集I(itemset)[14]: 事务数据库中个不同项目组成的集合, 记作, 其中的每个项目相当于一种商品.

定义2. 设有项目, 包含项目的所有事务的标识符的集合称为项目的Tidset. 在这种数据表示方法中, 数据库的事务由项目和该项目的Tidset组成, 该事务有项目唯一标识.

定义3.垂直型布尔矩阵

对于任意给定的事务数据库, 令:

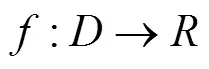
因此, 事务数据库经过一次扫描后, 就经上述定义映射为垂直型布尔矩阵.

2.2 支持计数计算

若项集的出现频率大于或等于min-sup与中事务总数的乘积, 称项集满足最小支持度min-sup, 若项集满足最小支持度, 则称为频繁项集集. 频繁-项集通常记作L.

支持计数通过两个项集的Tidset的“与”运算后得的矩阵与权重的乘积得到, 因此关联规则的支持计数定义为:

性质1: 频繁项集的所有非空子集都必须是频繁的.

性质2: 在数据库中若有一事务T其长度小于+1, 则由项集生成+1项频繁项集事务T是没有必要扫描的.

性质3: 由-1项集生成项集时, 当作自身连接时, 若两个项集的前-2项不同, 则放弃连接运算, 因为产生的项集不是重复的就是非频繁项集.

2.3 改进Inter-Apriori算法的主要思想

(1) 频繁1-项集. 扫描事务数据库一次, 将事务数据库利用定义1映射为垂直型布尔矩阵, 同时在矩阵前加一行全为1的权值; 矩阵后加一列count记录该商品出现次数,加一行sum-c, 记录每个事务所包含的项目数. 把不满足最小支持度的行(count列中min-sup所在的行)删去, 得到矩阵(布尔矩阵和sum-c行), 得到频繁1-项集.

(2) 剪枝. 首先, 合并矩阵中相同列, 即对整个矩阵中相同列进行整体合并, 得出合并后的矩阵及合并后的相同列所在的位置, 根据位置对矩阵应列的权值累加; 其次. 查找sum-c行大于或等于的位置, 把小于的列删去, 得到无重复列且每个事务所包含的项目数大于或等于的矩阵D.

(3) 频繁项集挖掘, 由-1项集挖掘-项集, 按照性质3进行连接. 对应的行进行“与”运算, 利用定义4计算支持计数. 重复过程2,3直至生成的频繁项集为空.

2.4 改进的Inter-Apriori算法

输入: 事务数据库; 最小支持度min-sup

2.5 实例分析

假定最小支持计数为2, 表1记录了9个顾客购买5种商品的具体情况.

表1 事务数据库

(1) 事务数据库映射为垂直型布尔矩阵, 并计算每个项的支持数count, 在矩阵的第一行给每个项集赋权值, 并在矩阵的最后一列sum-c, 记录每个事务所包含的项目总数. 如表2所示.

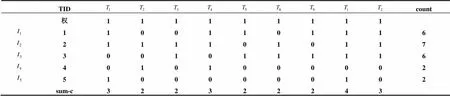
表2 垂直型布尔矩阵

(2) 扫描表2, 把不满足最小支持度的行(count列中min-sup所在的行)删去, 得到频繁1-项集, 并合并相同的列, 相应改变权值. 得到频繁1-项集,如表3所示

表3 频繁1-项集

(3) 描表3, 进行连接, 并且相应的列进行“与”运算, 如项集,, 支持计数为, 因此是频繁2-项集. 如表4所示.

表4 频繁2-项集

(4) 合并频繁2-项集矩阵中相同的列, 查找sum-c行大于或等于3的位置, 删去不符合条件对应的列. 得到剪枝后的频繁2-项集, 为挖掘频繁3-项集减少了计算量. 如表5所示.

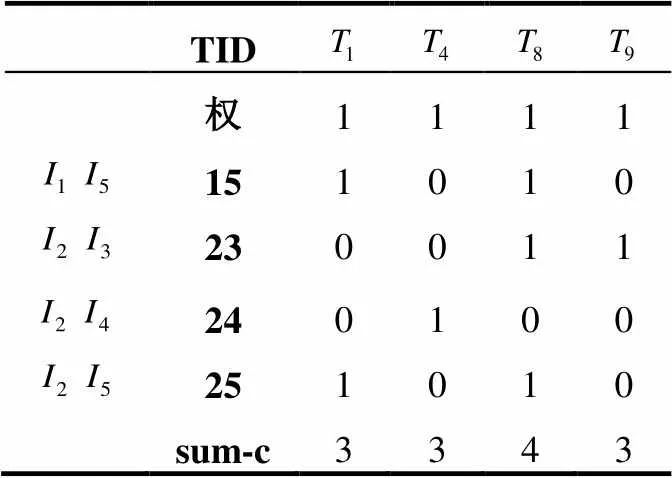
表5 剪枝后频繁2-项集

表6 频繁3-项集

(6)利用上述⑷的步骤, 整理频繁3-项集后得到剪枝后频繁3-项集, 因为中项集的个数为2<4, 所以算法终止. 如表7所示.

表7 剪枝后频繁3-项集

3 改进算法的性能分析

Inter-Apriori算法和改进的算法都将事务数据库映射为垂直型矩阵, 实现了仅扫描一次数据库; 其次, 由-1-项集连接生成-项集时, 若满足两个项集的前项不同, 则放弃连接运算, 避免产生过多的候选项集, 同时减少了扫描项集的次数, 有效的提高了算法的挖掘效率.

Inter-Apriori算法和本文算法的不同主要有:

(1)在空间复杂性上: Inter-Apriori算法将产生的项集存储在内存中, 而本文算法利用布尔矩阵进行存储, 记录样本占用更少的空间; 同时, 利用性质2和性质3对候选项集进行剪枝缩小了原布尔矩阵的规模, 也将占用更少的存储空间.

同时, Inter-Apriori算法是利用Tidset集取交集, 而本文算法对布尔矩阵进行“与”运算, 效率较高.

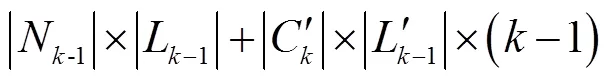
而Inter-Apriori算法利用性质3的计算量为:

3.1 实验环境

为了验证本算法的性能, 将其与Inter-Apriori算法作对比. 实现环境: 7GHZCPU, 2G内存和Windows XP操作系统, 程序用matlab语言实现. 实验数据集[15]来自IBM Almaden实验室生成的T10I4D100K和UCI机器学习数据仓库, 选择大小不同的四个事务数据集, 分别为两个稠密的Mushroom、Chess和两个稀疏的Nursery、T10I4D100K(取前22000个项目), 如表8所示.

表8 四种数据集

3.2 实验结果

根据数据集的稠密性, 不同的数据集给定不同的支持度, 然后分别测试挖掘频繁项集所消耗的时间和空间, 四种数据集的测试情况如图1.

图1 四种数据的运行时间

从时间复杂度上看, 改进的算法时间消耗比Inter-Apriori算法较少, 性能优势比较明显, 同时, 时间复杂度也明显降低了. 因为支持度越大时, 产生的频繁项集越少. 在支持度较小的情况下, 对于密集型数据集Mushroom与Chess, 改进后的算法运行时间变化缓慢, 而Inter-Apriori算法的变化趋势较大. 但是对于稀疏型数据集Nursery与T10I4D100K, 随着支持度不断变化的过程中, 在运行时间上, 改进后的算法明显优于Inter-Apriori算法.

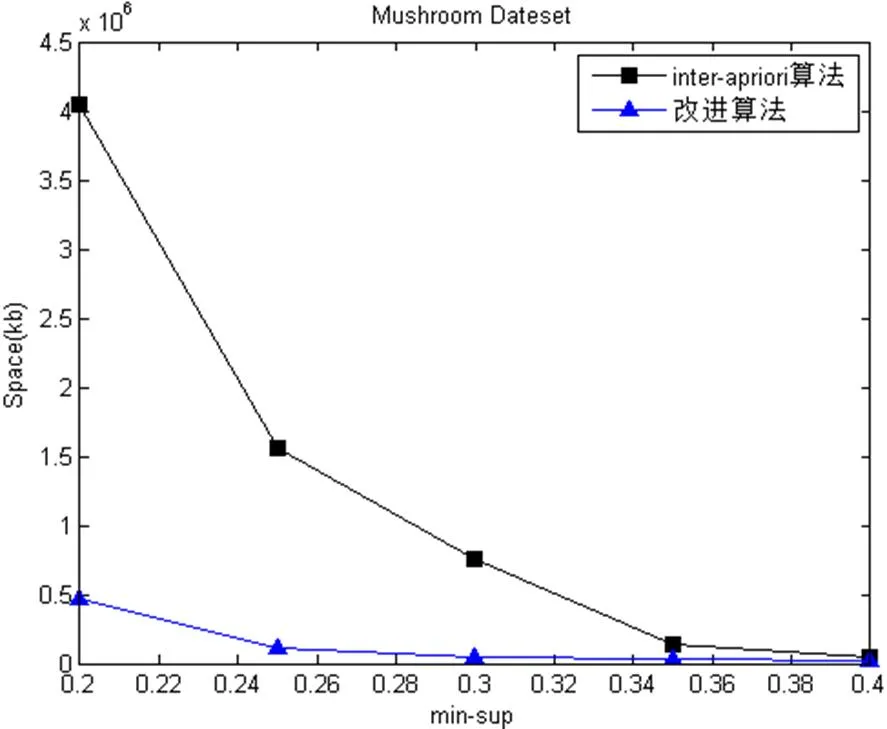
图2 四种数据的运行所占的内存

从空间复杂度上看, 改进后的算法明显比Inter-Apriori算法少. 因为支持度越大时, 产生的候选项集少, 进而产生的频繁项集越少, 算法运行所占的空间存储也越少. 在支持度较小的情况下, 对于密集型数据集Mushroom与Chess, 改进后的算法运行内存变化接近平缓, 而Inter-Apriori算法的变化趋势较大. 但是对于稀疏型数据集Nursery与T10I4D100K, 随着支持度不断变化的过程中, 在运行内存上, 改进后的算法明显优于Inter-Apriori算法.

由图1和图2测试结果可知, 改进算法的性能优于Inter-Apriori算法. 无论是稀疏型还是密集型数据集,随着minsup不断减小的过程中, 改进算法的性能和Inter-Apriori算法的性能差距逐步扩大, 也体现了改进后的算法良好的可伸缩性.

4 结论

本文建立了一种基于垂直型布尔矩阵的数据存储结构的挖掘算法, 利用定位和改变权值的大小, 来减少候选项目集的扫描时间和空间存储的复杂度, 并且通过不同稠密度及规模的Mushroom、Chess、 Nursery、T10I4D100K数据集, 从时间和内存上, 对两种算法性能进行了比较, 实验结果证明了改进算法的性能比Inter-Apriori算法要高.

1 范明,范宏建.数据挖掘导论.北京:人民邮电出版社,2011.

2 Agrawal R, Imielinaki T, Swami A. Mining association rules between sets of items in large databases. Proc. of ACM SIGMOD Conference on Management of Data. Washington, USA. ACM Press. 1993.

3 胡维华,冯伟.基于分解事务矩阵矩阵的关联规则挖掘算法.计算机应用,2014,3(S2):113–116.

4 苗苗苗,王玉英.基于矩阵压缩的Apriori算法改进的研究.计算机工程与应用,2013,49(1):159–162.

5 罗丹,李陶深.一种基于压缩矩阵的Apriori算法改进的研究.计算机科学,2013,40(12):75–79.

6 黄龙军,段隆振,章志明.一种基于上三角项集矩阵的频繁项集挖掘算法.计算机应用研究,2006,11:25–26.

7 荀娇,徐连成,杨仁华.基于排序索引矩阵的频繁项集挖掘算法.计算机工程,2012,38(19):41–44.

8 张玉芳,熊忠阳.Eclat算法的分析及改进.计算机工程, 2010,36(23):28–30.

9 徐嘉莉,杨洪军,赵茂娟,樊云.一种基于位运算的频繁闭项集挖掘算法.计算机应用研究,2013,11(30):80–82.

10 张文东,尹金焕,等.基于向量的频繁项集挖掘算法研究.山东大学学报(理学),2011,3(46):31–34.

11 刘步中.基于频繁项集挖掘算法的改进与研究.计算机应用研究,2012,36(2):475–477.

12 纪怀猛.基于频繁2项集支持矩阵的Apriori改进算法.计算机工程,2013,39(11):183–186.

13 熊忠阳,陈培恩,张玉芳.基于散列布尔矩阵的关联规则Eclat改进算法.计算机应用研究,2010,27(4):1323–1325.

14 Chen J, Xiao K. BISC: A bitmap itemset support counting approach for efficientfrequent itemset mining. ACM Trans. on Knowledge Discovery from Data, 2010, 4(3).

15 Goethals B. Frequent itemset mining dateset repository. http://fimi.ua.ac.be/date. [2004-12-02].

Improved Inter-Apriori Algorithm

CUI Shuang-Mi, ZHANG De-Sheng

(College of Science, Xi’an University of Technology, Xi’an 710054, China)

This paper establishes a mining algorithm based on the location and weight transaction item sets. It needs to scan the transaction database once. The algorithm adopts the vertical Boolean matrix to store transaction data, and the logic “and” operation and weight to calculate the support. Then it prunes through the searching location and combining the same columns of transaction matrix. Thereby the storage space and computing time used by the algorithm in the mining process can be reduced. The experimental results show that the improved algorithm performance has been significantly improved.

frequent itemsets; vertical type Boolean matrix; Inter-Apriori algorithm

国家自然科学基金(51379172)

2016-04-07;收到修改稿时间:2016-06-12

[10.15888/j.cnki.csa.005560]