航天器交会系统非脆弱滤波器的设计
程权成
(辽宁机电职业技术学院 华孚仪表学院,辽宁 丹东 118009)
航天器交会系统非脆弱滤波器的设计
程权成
(辽宁机电职业技术学院 华孚仪表学院,辽宁 丹东 118009)
针对航天器交会控制系统的滤波控制问题,利用Lyapunov函数方法、线性矩阵不等式(LMI)技术,运用H∞滤波控制理论,设计满足性能要求的非脆弱H∞滤波器。仿真实验表明,非脆弱H∞滤波器系统稳定、有效。
航天器交会系统;LMI;非脆弱;滤波器
Abstract:Considering the fi ltering problem of spacecraft rendezvous system, a non-fragile fi ltering in accordance with the function requirement is designed via linear matrix inequality (LMI) method and Lyapunov function method with the application of H∞ theory. The simulation experiment shows that the non-fragile fi ltering system is stable and effective.
Key words:Spacecraft rendezvous system; LMI; Non-fragile; H∞fi ltering
0 引 言
交会控制是航天器空间控制的关键技术之一,航天器交会控制问题受到学者的广泛关注。为解决航天器交会的实际工程技术需求,张莹瑾等提出一种合作目标定位方法,取得了较高的精度[1];针对航天器椭圆轨道,刘伟杰等采用线性定常增益进行航天器自主交会鲁棒控制器的设计方法研究[2];张卓等通过Lyapunov函数证明航天器交会系统的稳定性,进一步研究多个航天器交会时的协同控制问题[3]。关于滤波器设计问题的研究也有诸多成果。针对航天器交会对接系统,李艳辉等研究鲁棒H∞滤波器的相关设计问题[4];文献[5]针对连续非线性T-S模糊系统,对H∞滤波问题进行研究;文献[6]针对离散模糊系统,提出一种新的方法来保证滤波系统的稳定性。此外,由于MATLAB软件的强大运算功能,该软件一直是控制领域相关研究人员的主要使用工具[7]。随着MATLAB软件中线性矩阵不等式(LMI)工具箱的出现,LMI技术的应用逐步广泛,在一定程度上促进了LMI技术在控制理论相关领域的应用。本文以航天器交会控制系统为研究对象,利用Lyapunov函数方法、LMI技术,运用H∞滤波控制理论及非脆弱滤波控制理论,推导出非脆弱H∞滤波器存在的矩阵不等式条件,设计航天器交会系统非脆弱H∞滤波器。
1 问题描述
两个航天器进行交会对接的相对运动状态方程见(1)式,针对该系统方程的交会系统进行滤波器的设计[8]。
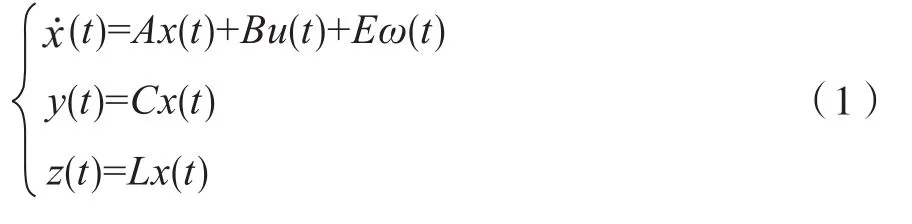
其中,x(t)=[OxOyOzO O Oż]T为系统的状态变量,Ox, Oy, Oz是追踪航天器相对于目标航天器的位置坐标; u(t)=[TxTyTz]T为系统的控制变量输入,Tx, Ty, Tz是作用于追踪航天器三个坐标轴的控制推力;ω(t)为系统的干扰变量;y(t)为系统的测量输出变量;z(t)为待估计信号变量;A, B, C, E, L为系统的系数矩阵。

这里,n是目标航天器绕地飞行的角速度,m是目标航天器的质量。
针对航天器交会对接系统的滤波问题,在滤波器的设计过程中,一般假定系统(1)式是稳定的,因而考虑如(2)式所描述的状态反馈控制器系统模型,以保证航天器交会对接系统的稳定性。

其中K为使系统稳定的控制器矩阵增益参数。
将(2)式代入(1)式中,经过数学方法处理后可得到系统模型为:

为实现航天器交会系统的滤波控制,采用的滤波器结构为:

其中,AF, BF, CF为需要设计的滤波器参数增益;xF(t)为滤波器的状态向量;zF(t)为滤波器的估计变量。ΔAF, ΔBF, ΔCF为滤波器模型中的参数不确定性变量,且具有形式ΔAF=HAFFAF(t)EAF, ΔBF=HBFFBF(t)EBF,为已知的定常矩阵,为时变参数,且满足
定义新的变量ξT(t)=[x(t) xF(t)]T,e(t)=z(t)-zF(t),综合系统模型(3)式和滤波器结构(4)式,得到滤波系统模型为:

在考虑非脆弱问题的情况下,设计H∞滤波器增益,使其满足当ω(t)=0时,滤波系统模型(5)式是渐进稳定的,同时对于γ>0,有不等式关系[5],即:
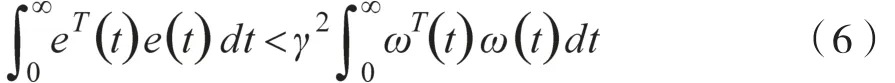
主要结论的推导过程使用了以下三个引理:
引理1[11]已知对称矩阵可得出结论,不等式条件(7)式和(8)式等价。

引理2[12]对于给定适当维数的实矩阵W=WT, H,E, ΔTΔ≤I,可得出结论,存在任意的常数ε > 0,使其满足不等式关系:

引理3当ω(t)=0时,对于系统模型(3)式,若存在矩阵X > 0,Y使得不等式成立,即:

则系统模型(3)式是渐进稳定的,且K=YX-1。
证明选取Lyapunov函数:

对Lyapunov函数求导可得:
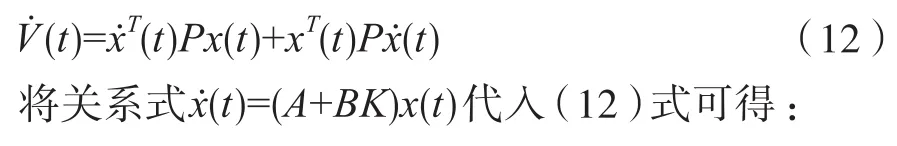

因此,若要保证系统模型(3)式是稳定的,则只需不等式成立,即:

定义矩阵变量X=P-1, Y=KX,对不等式左右分别乘以X和它的转置,则可得到引理3所述的条件。
需要说明的是,引理3的主要意义在于可求解出控制器矩阵参数K,进而保证系统模型(3)式是稳定的,使其满足滤波器设计的前提条件。
2 非脆弱滤波器的设计
先推导实现非脆弱H∞滤波器的不等式条件,再通过LMI方法,得出非脆弱滤波器的矩阵不等式的设计条件。
定理1对于航天器交会滤波系统模型(5)式,对于给定的H∞性能指标γ>0,若存在矩阵G>0,使得下列矩阵不等式成立,即:

可见,航天器交会滤波系统模型(5)式是稳定的,且满足H∞性能指标,其中, , , 的定义见(5)式。
证明若要实现H∞滤波器的设计,则需满足H∞性能指标:

定义Lyapunov函数:

根据Lyapunov函数,可得出结论,即φ(0)=0,且φ(∞) > 0,进而得出关系式:
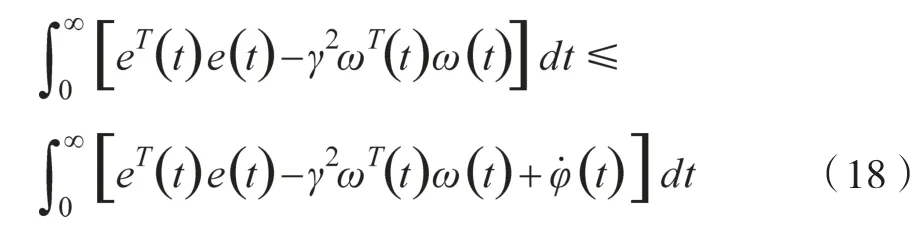
为使滤波系统的H∞性能得到保证,只要满足不等式关系:

将系统模型(5)式代入(19)式中,可得到不等式关系:


若不等式(21)式成立,那么不等式(20)式也成立。
对不等式(21)式运用引理1,便可得到定理1所述的不等式条件。定理1证毕。
需要说明的是,定理1给出了滤波系统模型(5)式满足H∞稳定的不等式条件,但该条件不能求解出滤波器的参数,故需要进一步处理,即给出定理2的条件。
定理2利用LMI方法,推导出非脆弱H∞滤波器存在的矩阵不等式条件。
定理2对于航天器交会滤波系统模型(5)式,对于给定的H∞性能指标γ > 0,若存在矩阵G1, G2, R, S,T及常数λ,ε > 0使得下列矩阵不等式成立:

其中П=G1A+ATG1+G1BK+KTBTG1+SC+CTST,那么航天器交会滤波系统模型(5)式是稳定的,且满足H∞性能指标,滤波器的参数增益为:
证明定义矩阵变量,同时将,及G代入定理1,然后定义矩阵变量R=G2AF,S=G2BF, T=CF,可得到不等式:

根据滤波器模型中的参数不确定性变量的定义,可将矩阵不等式(24)式改写为矩阵不等式:

对不等式(25)式运用引理2和引理1,便可得到定理2所述的不等式条件。定理2证毕。
3 仿真实验
为进一步证明滤波器设计方法的有效性,选取数值实例进行仿真分析。假设追踪航天器的质量m=300kg,目标航天器的轨道角速度为n=7.2722×10-5rad/s,假定滤波器模型中存在的不确定参数为:

通过Matlab软件中LMI工具箱求解定理2中非脆弱H∞滤波器存在的矩阵不等式条件,计算得出滤波器增益参数为:

图1 滤波器状态向量的响应曲线
4 结 论
本文将非脆弱滤波器设计技术引入到两个航天器交会系统的应用中,针对航天器交会控制系统的滤波控制问题,利用Lyapunov函数方法、LMI技术及H∞滤波控制理论,设计满足性能要求的非脆弱H∞滤波器。所设计的滤波器增益参数存在条件通过LMI的形式给出,通过Matlab软件中LMI工具箱直接求解。通过Matlab软件的simulink技术对所设计的滤波器系统进行仿真实验,结果表明,当滤波器中时变矩阵参数改变时,系统仍能保持稳定,具备较强的非脆弱性。下一步将研究多个航天器交会控制问题,不断增强其实际应用性。
[1] 张莹瑾,秦世引,胡晓惠.航天器自主交会对接的高精度目标定位方法[J].宇航学报,2014,35(12):3-6.
[2] 刘伟杰,谌颖.航天器椭圆轨道自主交会的鲁棒H∞控制[J].宇航学报,2015,36(2):179-185.
[3] 张卓,张泽旭,谭浩.基于鲁棒协同控制方法的多航天器交会问题[J].深空探测学报,2016,3(1):90-96.
[4] 李艳辉,刘畅.网络环境下航天器交会对接系统的鲁棒H∞滤波[J].中国惯性技术学报,2015,23(4):522-526.
[5] XIE X P,ZHU X L,GONG D W.Relaxed Filtering Designs for Continuous-time Nonlinear Systems Via Novel Fuzzy H∞Filters[J].Signal Processing,2013,93(5):1251-1258.
[6] ZHANG J,XIA Y.New LMI Approach to Fuzzy H∞Filter Designs[J].IEEE Transactions on Circuits and Systems—II:Express Briefs,2009,56(9):739-743.
[7] 田丰.基于自适应信号处理技术的有源电力滤波器控制方法[J].温州职业技术学院学报,2016,16(2):51-54.
[8] 高会军,杨学博,王常虹.一种有限推力航天器交会轨道的鲁棒设计方法[J].空间控制技术与应用,2009,35(2):3-6.
[9] WO S,ZOU Y,CHEN Q,et al.Non-fragile Controller Design for Discrete Descriptor Systems[J].Journal of the Franklin Institute,2009,346(9):914-922.
[10] 程权成,常晓恒.T-S模糊系统非脆弱跟踪控制器设计[J].电子设计工程,2014,22(17):1-4.
[11] BOYD S,GHAOUI L E,FERON E,et al.Linear Matrix Inequalities in System and Control Theory[M].Philadelphia:Society for Industrial and Applied Mathematics,1994:57-63.
[12] PETERSEN I R.A Stabilization Algorithm for a Class of Uncertain Linear Systems[J].Systems & Control Letters,1987,8(4):351-357.
[责任编辑:乔维德]
Design of Non-fragile Filtering for Spacecraft Rendezvous System
CHENG Quancheng
(School of Huafu Meter Instrument, Liaoning Mechatronics College, Dandong, 118009, China)
V526
A
1671-4326 (2017) 03-0062-05
10.13669/j.cnki.33-1276/z.2017.058
2017-02-06
辽宁机电职业技术学院科研项目(2017010)
程权成(1989—),男,辽宁辽阳人,辽宁机电职业技术学院华孚仪表学院,助理工程师,硕士.

