基于计算流体力学的车辆发动机散热器芯部外形优化

索文超， 许翔， 耿飞

(1.陆军航空兵学院 预选士官训练基地, 北京 101123; 2.军事交通学院 军用车辆系, 天津 300161)

基于计算流体力学的车辆发动机散热器芯部外形优化

索文超1， 许翔2， 耿飞1

(1.陆军航空兵学院 预选士官训练基地, 北京 101123; 2.军事交通学院 军用车辆系, 天津 300161)

为降低散热器空气侧流动阻力和芯部体积以达到节约冷却风扇功率和车辆动力舱空间的目的，建立了散热器空气侧计算流体力学(CFD)模型和基于CFD分析的散热器芯部外形优化模型。在满足散热需求和动力舱安装空间要求的前提下，以空气侧流动阻力和芯部体积为目标函数，基于遗传算法对一板翅式散热器芯部外形进行了优化，对优化后散热器的散热性能进行了校核。结果表明，所建优化模型是可行的。采用正交试验设计法确定了各变量对优化目标影响的主次顺序：在空气流量一定时，散热器芯部高度对散热器空气侧流动阻力和芯部体积的影响最为显著。

动力机械工程； 散热器； 计算流体力学； 遗传算法； 外形优化

Abstract: A radiator air side CFD model and an optimization model of radiator core shape based on CFD are established for reducing the airflow pressure drop and the volume of vehicle engine radiator core to save the cooling fan power and the vehicle engine compartment space. Under the precondition of satisfying the requirement of heat dissipating capacity, the shape of a plate-fin radiator core is optimized based on genetic algorithm by taking the air side pressure drop and the volume of its core as the target functions. The heat dissipation performance of the optimized radiator was verified. The optimized results show that the proposed optimization model is feasible. The primary and secondary sequences of the variables affecting the optimization targets are found by using an orthogonal experimental design method. And the height of radiator core has the most significant influence on the air side pressure drop and the volume of radiator core when the air flow rate is constant.

Key words: power machinery engineering; radiator; computational fluid dynamics; genetic algorithm; shape optimization

0 引言

散热器是车辆冷却系统的重要部件，其芯部结构参数确定后，需要着重解决在车辆总体限定的安装空间内，安排出足够的散热面积以满足散热要求；同时要尽可能降低散热器空气侧的流动阻力和芯部体积，以达到节约冷却风扇功率和车辆动力舱空间的目的。其中的关键就是要合理确定散热器的正面面积和厚度，这是一个不断优化的过程[1]。

计算流体力学(CFD)与优化算法在散热器空气流动与传热及其优化设计方面应用十分广泛，通常做法为：针对不同方案分别进行CFD的分析对比[2-4]；分别实施优化过程与CFD分析以完成结构优化与性能分析[5-7]；将CFD分析、近似公式与序列二次规划法相结合以完成优化设计[8]等。以上研究未能将CFD分析与优化算法进行有效结合，或者由于使用了近似公式而容易带来误差影响。本文以芯部结构参数已定的某大功率车辆发动机水散热器为对象，分别建立了散热器空气侧CFD模型和基于CFD分析的散热器芯部外形优化模型，通过编制程序控制CFD软件来自动完成散热器CFD模型的几何建模、边界设置和CFD求解等过程；通过CFD分析与优化算法相结合，对散热器芯部外形进行了优化；对优化后散热器的散热性能进行了校核，以保证满足散热需求；最后采用正交试验设计法确定了优化目标各影响因素的主次顺序。

1 散热器空气侧CFD模型

大功率发动机散热器芯部体积庞大、冷热流体通道相对非常微小，难以实现整体三维建模及网格离散。在针对散热器芯部建立CFD模型时，通常利用散热器芯部结构的几何对称性与周期性，采用对称边界和周期性边界对计算区域进行简化[3-9]。基于此方法，文献[9]对一管片式散热器建立了空气侧CFD模型并进行了验证，计算结果表明，所得空气侧流动阻力的模拟值与试验值最大相对误差为8.24%，验证了该模型的可行性。

本文以一叉流型板翅式水散热器为研究对象，其空气侧翅片为多折型百叶窗式翅片，水侧翅片与空气侧结构相同，但不开百叶窗。相关参数定义如下：散热器芯部外形长度为L、宽度为W、高度为H，芯部体积为V；翅片(隔板)厚度为δ、高度为h，节距为b、节距数为Nb、层数为N、散热面积为As、流体流通面积为Ac、芯部正面面积为Af、空气侧翅片百叶窗间距为d、百叶窗间隙为c. 通过添加下角标a、w和p对空气侧翅片、水侧翅片和隔板的参数进行区别。图1为散热器芯部结构示意图，图2为空气侧翅片结构及主要参数标注情况。

参照文献[9],计算区域确定如下：H向(空气流动方向)取散热器芯体的全长；W向取半层空气层的高度；L向取空气侧翅片一个节距的长度。入口边界设置为质量流量入口边界，出口边界设置为压力出口边界，壁面热边界条件处理采用第2类热边界条件，即输入热流密度。计算区域的选取及其余边界设置情况如图3所示。

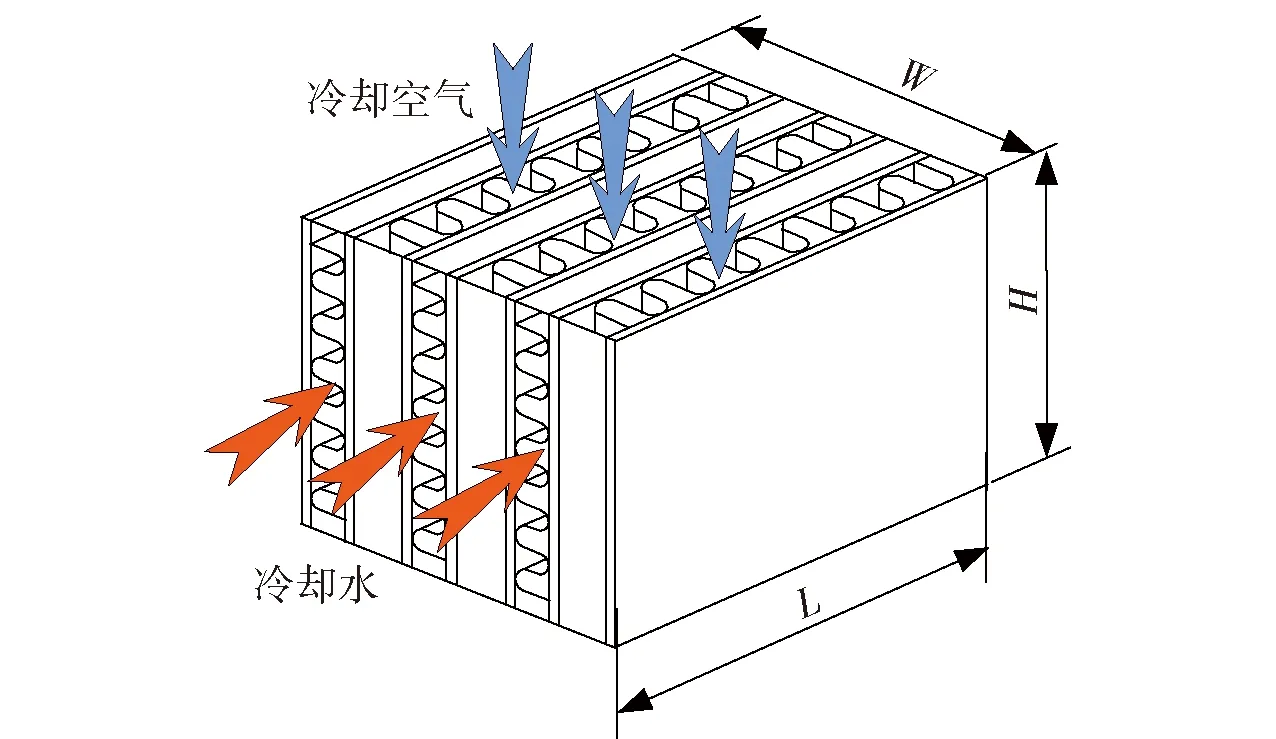
图1 散热器芯部结构示意图Fig.1 Schematic diagram of radiator core structure

图2 空气侧翅片结构及主要参数标注图Fig.2 Air-side fin structure and its parameters

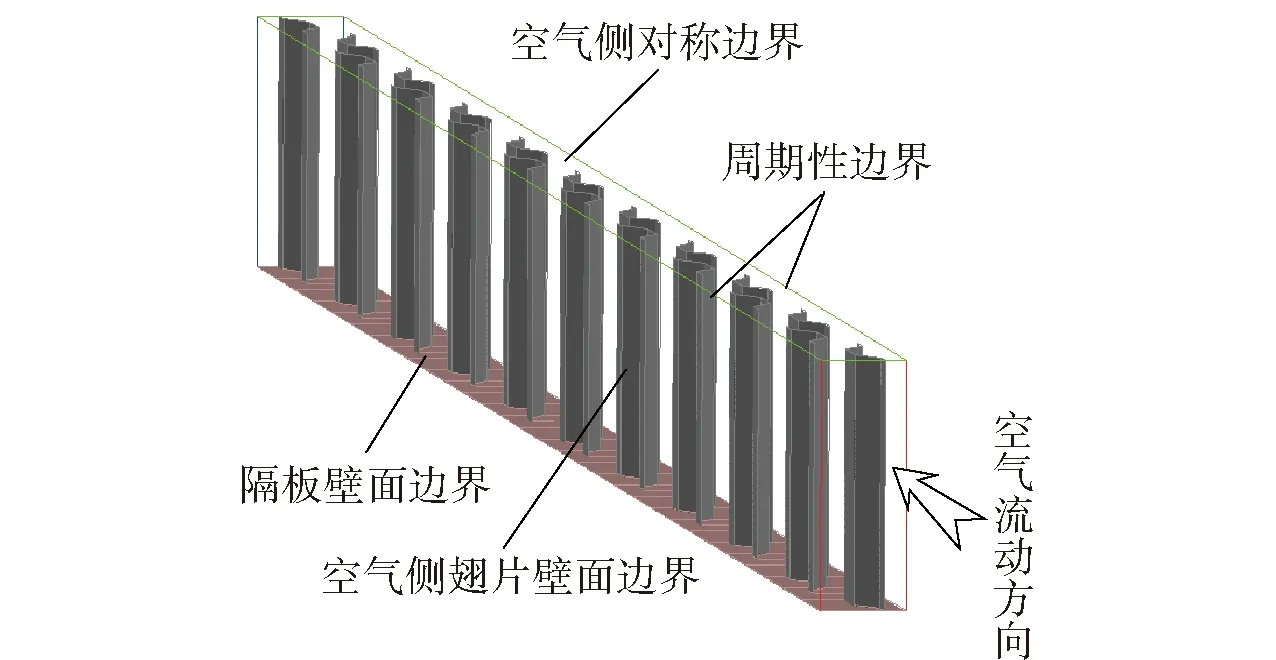
图3 计算区域的选取及边界设置Fig.3 Computation domain and boundary

模型基于三维直角坐标建立，并作如下假定：1)流动为稳态流动，散热器空气侧入口处空气速度均匀分布，相邻空气侧流道内气体的流动特性非常接近；2)空气侧散走的总热量在各散热表面均匀分配；3)翅片与隔板(水管)的焊接情况良好，接触部分之间不存在缝隙或突起；4)忽略翅片厚度对流动的影响；5)空气为不可压缩气体，物性参数只随温度而发生改变；6)辐射换热与重力影响忽略不计。

计算基于空气流动的质量守恒方程、动量守恒方程、能量守恒方程及标准k-ε湍流模型建立控制方程，采用基于压力耦合式算法进行CFD求解，控制方程的离散格式为2阶迎风格式。

2 优化模型的建立

2.1 基本思路

优化以满足散热要求为前提。首先，根据已知条件进行热平衡估算，并根据散热器安装位置的空间尺寸限制来确定约束条件；然后，选取设计变量和目标函数并优化求解；最后，根据优化结果对散热器的散热性能进行校核，以确保优化后仍能满足设计要求。图4为散热器芯部外形优化过程框图。

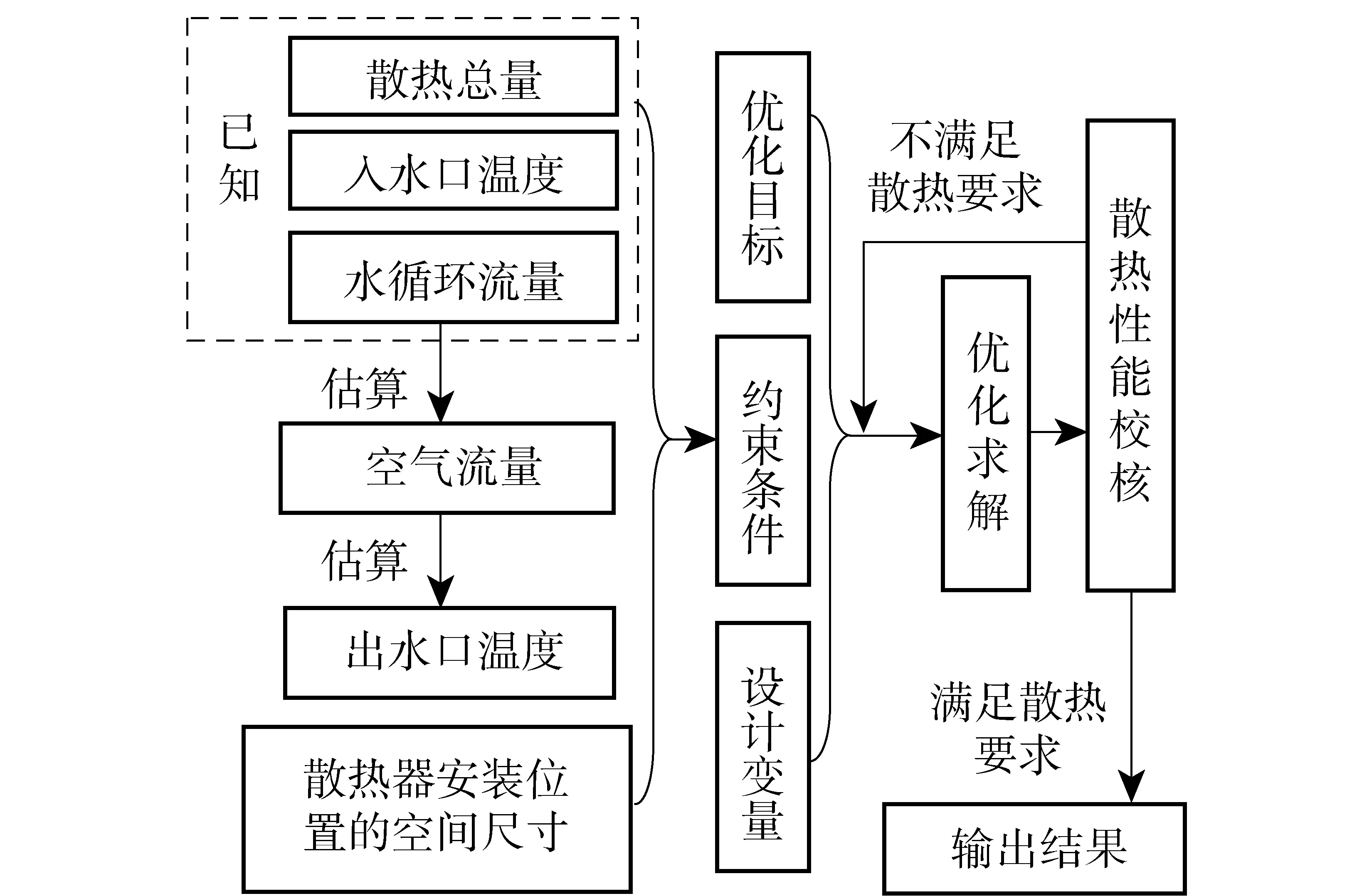
图4 优化过程框图Fig.4 Block diagram of optimization process

2.2 热平衡估算

为保证散热器满足发动机冷却系统的散热要求，通过热平衡估算确定相关参数。

2.2.1 已知条件

散热器内冷却水需要散走的总热量为Φw，散热器入水口温度为Ti,w，水循环流量为qm,w.

2.2.2 估算冷却空气流量

散热器在稳态工作时，不考虑散热器的热损失，散热器冷却水放出的热量Φw可认为全部由冷却空气带走，即冷却空气带走的热量Φa与冷水放出的热量Φw相等。冷却空气流量的大小一般由(1)式确定：

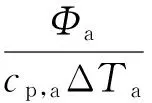
(1)

式中：qm,a为空气质量流量；cp,a为空气定压比热容；ΔTa为空气进出口温差，参考同类车辆水散热器的空气侧温升可对ΔTa做出近似估计。

2.2.3 确定入水口与出水口温度差

水侧同样满足(1)式的关系，则入水口与出水口温度差满足(2)式：

(2)

式中：qm,w为水循环流量；cp,w为水定压比热容。

2.3 目标函数

为减小散热器的空气侧流动阻力Δp和体积V，达到节约冷却风扇功率和车辆动力舱空间的目的，在满足散热要求的条件下，将空气流动阻力最小和芯部体积最小作为目标函数，按照线性加权组合法，将多目标函数转化为如下单目标函数形式：

(3)

式中：ωi为各目标函数的权重因子，i=1,2；Si为各目标函数的无因次系数。

2.4 设计变量

为正确选定散热器合理的正面面积和厚度，初步选取长方体状散热器芯体的长L、宽W、高H3个外形尺寸作为设计变量。如图1所示，板翅式散热器芯部结构为空气层与水层依次交替，且层与层之间均有隔板隔开，散热器芯部宽度W的计算式可表示如下：

W=haNa+hwNw+δpNp,

(4)

式中：ha为空气侧翅片高度；Na为空气侧层数；hw为水侧翅片高度；Nw为水侧层数；δp为隔板厚度；Np为隔板层数。

根据散热器芯部结构的规律性，空气侧层数Na、水侧层数Nw和隔板层数Np三者之间有着确定的数学关系，因此，只要确定了空气侧层数Na，即可确定另外两个层数。由于空气侧翅片高度ha、水侧翅片高度hw和隔板层厚度δp均已确定，因此，只要确定了空气侧层数Na，就可以确定散热器芯部宽度W.

由于散热器芯部宽度W是由空气侧层数Na决定的，改用空气侧层数Na代替芯部宽度W作为设计变量，可以避免芯部宽度的优化结果出现半个层数或其他不符合实际的现象。

综上所述，最终选取散热器芯部长度L、芯体高度H和空气侧层数Na作为设计变量。其中，前两个参数为连续型变量，后一个参数为整型变量，其标准形式如下：

X={x1,x2,x3}T={L,H,Na}T.

(5)

3个设计变量决定了散热器芯部的正面面积Af和体积V；当芯部翅片结构一定时，3个设计变量还决定着空气侧和水侧的总散热面积As. 同时，散热器芯部的正面面积又决定了空气流通面积，在一定的空气流量下，也就决定了散热器芯部的正面空气速度。而散热器的空气流动阻力主要受正面空气速度与流道长度(即散热器芯部高度H)的影响，因此，3个设计变量又影响着空气流动阻力。综上分析可知，3个设计变量直接制约着两个目标函数。

2.5 约束条件

2.5.1 正面面积的约束

散热器芯部的正面空气速度u通常控制在设计范围内。根据前文给定的空气质量流量qm,a，通过(6)式即可对散热器的正面面积进行约束。

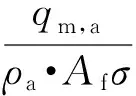
(6)

式中：ρa为空气密度；σ为散热器空气流通面积与其正面面积之比。

2.5.2 温度差的约束

为了得到冷热介质的温度差，通常采用算术平均温度差ΔTm进行估算，计算式如下：

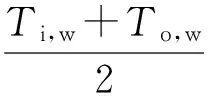
(7)

式中：Tw和Ta分别为散热器水侧和空气侧平均温度；Ti,w和To,w分别为散热器水侧入口温度和出口温度；Ti,a和To,a分别为散热器空气侧入口温度和出口温度。

由于CFD模型中没有建立水侧模型，而采用对固体壁面施加热边界条件的方式来模拟传热，空气侧与隔板平均温度差ΔT′m应小于空气层与水层的算术平均温度差ΔTm，否则将影响热量从水侧到空气侧的传递。ΔT′m按(8)式计算：

ΔT′m=Tp-Ta，

(8)

式中:Tp为隔板表面平均温度。

2.5.3 设计变量的约束

为提高计算效率，应尽可能缩小设计变量的搜索空间。根据散热器安装空间的限制，可确定L、Na和H的上限值。由于散热器芯部的正面面积Af与空气侧散热面积As,a均为散热器芯体外形尺寸的函数，即有

Af=f(L,Na)，

(9)

As,a=f(L,Na,H).

(10)

通过对散热面积、正面面积等条件的约束，可对L、Na和H的上限值、下限值做出进一步约束。

综上所述，所有约束条件汇总如下：

(11)

3 优化求解

3.1 边界条件的更新

根据新的设计变量更新边界条件，具体步骤如下：

1)确定芯部宽度W. 根据设计变量中的Na计算出W.

2)确定散热器芯部空气侧总的通道数Nc. 将散热器芯部空气侧翅片每一个节距的流通面积看作一个通道，则Nc可以按(12)式计算：

Nc=(L/ba)×Na.

(12)

3)确定空气侧总散热面积As,a. 由于CFD分析区域的入口横截面选取的是空气侧一个节距翅片的宽度和半个翅片高度，相当于选取了散热器芯部空气侧所有通道中的半个通道，根据CFD计算结果可读出空气侧翅片的面积At,a与隔板面积Ap，求和之后即为半个通道的散热面积。因此，总散热面积计算式为

As,a=(At,a+Ap)×2×Nc.

(13)

4)确定壁面边界的热流密度

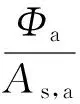
(14)

5)确定计算区域入口处的空气质量流量

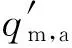
(15)

3.2 基于CFD分析的优化过程实现

优化过程采用优化软件、自编程序与CFD软件相结合进行。由C++语言编制的可执行程序将优化软件赋予的设计变量值处理为CFD求解所需的参数，并控制CFD软件自动完成散热器空气侧CFD模型的CFD求解过程，最后将计算结果整理为目标函数值并报告给优化软件。由于空气侧流动阻力通过CFD计算获得，没有明确的计算表达式，传统的优化方法受到限制。遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法，它直接以目标函数作为搜索信息，仅使用由目标函数值变换来的适应度函数值就可确定进一步搜索的方向和范围，对目标函数的性质几乎没有要求，算法的鲁棒性、可靠性和移植性好，因此本文的优化过程基于遗传算法进行，采用罚函数法处理约束条件。基于CFD分析的优化过程流程图如图5所示。

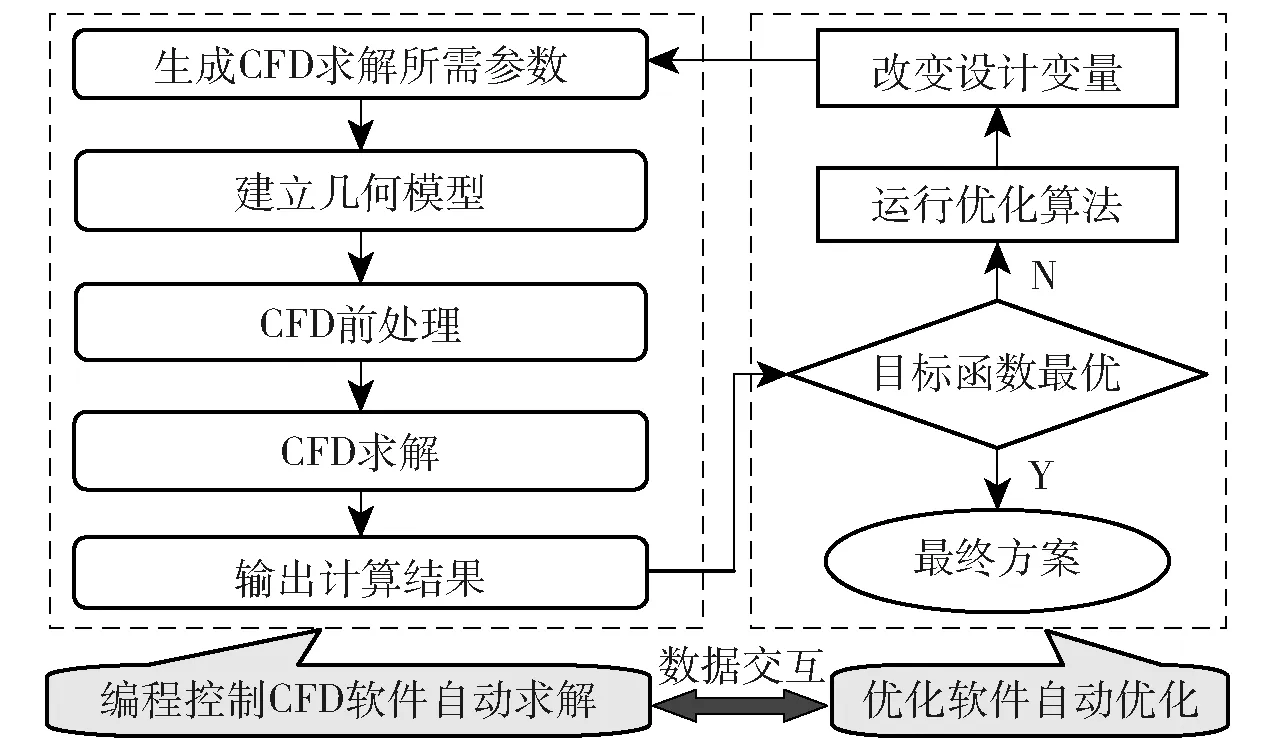
图5 基于CFD分析的优化过程流程图Fig.5 Flow chart of optimization process based on CFD

3.3 优化结果

为同时兼顾节约风扇功率和动力舱空间，优化过程中，认为散热器空气侧流动阻力和芯部体积两个分目标函数同等重要，其权重因子均取为1，并通过无因次系数将各目标函数无因次化，以消除各分目标因数量级差异所引起的权重失衡。

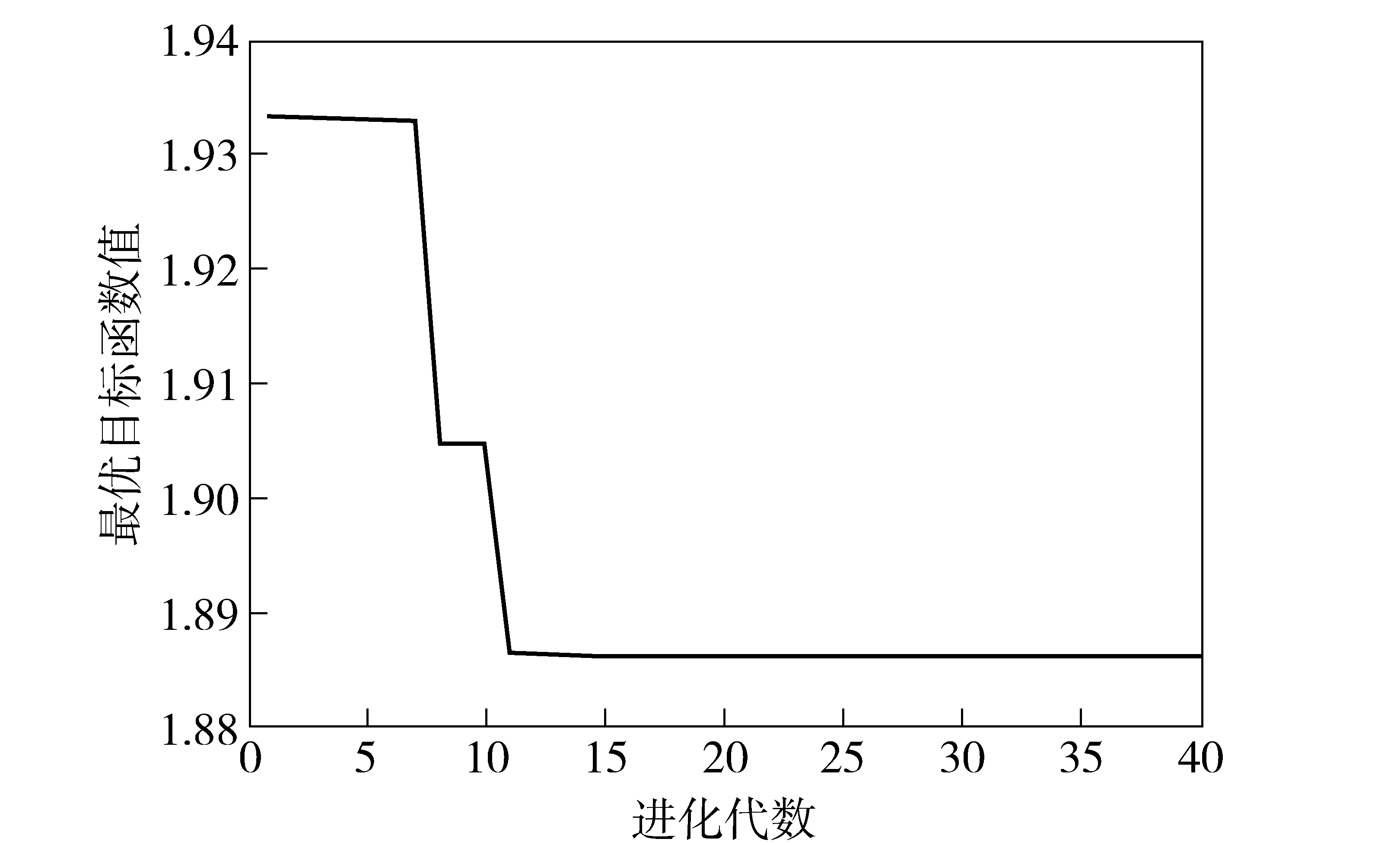
图6 遗传算法进化过程Fig.6 Evolutionary process of genetic algorithm

遗传算法的进化过程如图6所示。由图6可见，随着进化的逐代进行，最优目标函数值不断减小，尤其是在初始阶段，较差个体很快被淘汰，最优目标函数值下降明显，经过不断进化并最终趋于稳定。

在各参数取值区间内分别选取接近上限的一个值，将该值与各参数实际值之比作为该参数的无因次值。散热器各无因次参数值优化前后的对比情况如表1所示。优化后散热器空气侧流动阻力和芯部体积比优化前分别降低了6.95%和6.31%.

表1 优化前后参数对比

优化后，散热器芯部高度减小了6.67%，芯部高度的减小使得空气流道变短，从而降低了空气流动阻力；优化后，散热器正面面积增加了0.52%，正面面积的增加使得在同等空气流量下散热器的正面风速下降，也会促使散热器空气侧的流动阻力下降。因此以上因素促使优化后的散热器空气侧流动阻力比优化前下降了6.95%.

4 散热器散热性能校核

考虑到优化后的散热器正面风速下降以及芯部体积减小可能会影响到散热器的散热性能，因此对优化后散热器的散热性能进行校核。

根据优化结果，可以求出空气侧进口和出口处的空气温度，而水侧入口水温已知，因此需要校核出口水温是否满足设计要求。校核步骤如下：

1)列出优化后散热器的结构及相关物性参数，计算空气侧和水侧雷诺数；

2)根据空气侧和水侧雷诺数，确定两侧流体的换热系数αa和αw；

3)计算散热器传热表面的总效率η0,a和η0,w；

4)计算传热壁面的导热热阻R；

5)根据上述计算结果，计算总传热系数K；

6)根据优化后水侧散热面积As,w及总传热系数K,计算算术平均温度差ΔTm；

7)根据(7)式计算出散热器出口水温。

有关计算公式参见文献[1]。经校核，优化后散热器的散热性能能够满足散热要求。

5 灵敏度分析

为确定各设计变量对目标函数影响的主次顺序，采用正交试验设计法进行灵敏度分析。将3个设计变量全部作为因素，对每个因素取3个水平，按照L9(34)的要求共安排9次模拟计算实验。采用极差法确定各因素对优化目标影响的主次顺序，结果如表2所示。

表2 各变量对优化目标影响的主次顺序

分别对指标的平均值进行无因次处理，获得对应的无因次值。以因素水平为横坐标，以指标无因次值为纵坐标，可得出因素与指标关系如图7所示。

图7 因素与指标关系图Fig.7 Relationship among factors and targets

通过以上分析可知，在空气流量一定的情况下，影响散热器空气侧流动阻力和其芯部体积的各因素的主次顺序依次为散热器芯部高度、空气侧层数和芯部长度。其中，尤其以散热器芯部高度的影响最显著。因此，在散热器的芯部外形尺寸设计时应重点关注芯部高度的设计。

6 结论

本文所做研究工作的贡献和结论如下：

1)提出了一种基于遗传算法和CFD分析的优化设计方法。在优化过程中，通过编制程序控制CFD软件自动完成CFD分析过程，并实现了CFD分析过程与优化过程的数据交互。

2)以散热器空气侧流动阻力和芯部体积为目标函数，建立了基于CFD分析的散热器芯部外形优化模型。实例优化显示，优化后散热器空气侧流动阻力和芯部体积分别降低了6.95%和6.31%.

3)基于正交试验设计法的灵敏度分析结果表明，在空气流量一定时，散热器芯部高度是散热器空气侧流动阻力和芯部体积的主要影响因素。

References)

[1] 姚仲鹏, 王新国. 车辆冷却传热[M].北京: 北京理工大学出版社, 2001. YAO Zhong-peng, WANG Xin-guo. Vehicle cooling heat transfer[M]. Beijing: Beijing Institute of Technology Press, 2001. (in Chinese)

[2] 冯燕燕，李义林，王丽华. 基于Fluent仿真模拟的车辆散热器外形优化研究[J]. 北京汽车, 2015(3):43-46. FENG Yan-yan, LI Yi-lin, WANG Li-hua. Study on shape optimization of vehicle radiator based on Fluent[J]. Beijing Automotive Engineering, 2015(3):43-46. (in Chinese)

[3] 田杰安, 李世伟, 闫伟, 等. 基于CFD分析的散热器结构优化[J]. 内燃机与动力装置, 2012(4): 40-42,57. TIAN Jie-an, LI Shi-wei, YAN Wei, et al. Improvement of the radiator structure based on CFD analysis[J].Internal Combustion Engine & Powerplant, 2012(4): 40-42,57. (in Chinese)

[4] 李宇. 工程机械双流程散热器散热特性分析[D]. 长春：吉林大学, 2016. LI Yu. Research on heat transfer characteristics of the two-pass radiator for construction vehicle[D]. Changchun: Jilin University, 2016. (in Chinese)

[5] 张钦国. 工程车辆温控独立冷却系统关键技术研究[D]. 长春：吉林大学, 2016. ZHANG Qin-guo. Research on key techniques of independent temperature control cooling system for construction vehicle[D]. Changchun: Jilin University, 2016. (in Chinese)

[6] 张敏, 高婵. 基于计算流体动力学的板翅式散热器传热性能研究[J]. 机械强度, 2016,38(4):833-837. ZHANG Min, GAO Chan. Study on heat transfer performance of plate-fin radiator based on computational fluid dynamics[J]. Journal of Mechanical Strength, 2016, 38(4):833-837. (in Chinese)

[7] 郭健忠，徐敏，张光德，等. 汽车散热器的性能分析及翅片结构优化[J]. 科学技术与工程, 2016, 16(26):58-64. GUO Jian-zhong, XU Min, ZHANG Guang-de, et al. Performance analysis and optimization of automobile radiator fin structure[J].Science Technology and Engineering, 2016, 16(26):58-64. (in Chinese)

[8] 毕小平，李贺佳，索文超. 计算流体力学在水散热器芯部外形尺寸设计中的应用[J].内燃机工程，2010,31(1): 97-99. BI Xiao-ping, LI He-jia, SUO Wen-chao. Application of computational fluid dynamics in outline size design of water radiator core[J]. Chinese Internal Combustion Engine Engineering, 2010,31(1): 97-99. (in Chinese)

[9] 索文超，毕小平，李贺佳. 车用散热器空气流动阻力数值预测研究[J].汽车工程，2008,30(9): 800-803. SUO Wen-chao, BI Xiao-ping, LI He-jia. A study on the prediction of the airflow resistance for vehicle radiator[J]. Automotive Engineering, 2008,30(9): 800-803. (in Chinese)

OptimizationofRadiatorCoreShapeofVehicleEngineBasedonCFD

SUO Wen-chao1， XU Xiang2， GENG Fei1

(1.Primary Non-Commissioned Officer Training Base, Army Aviation Institute of PLA, Beijing 101123，China;2.Department of Military Vehicle, Military Transportation University, Tianjin 300161, China)

TK421+.12

A

1000-1093(2017)09-1839-06

10.3969/j.issn.1000-1093.2017.09.022

2017-02-03

索文超(1979—)，男，工程师，博士。E-mail：suowenchao@163.com