永磁轨道磁感应强度计算方法*
李海涛葛玉梅孙睿雪邓自刚
永磁轨道磁感应强度计算方法*
李海涛1,2葛玉梅1孙睿雪2邓自刚2
(1.西南交通大学力学与工程学院应用力学与结构安全四川省重点实验室,610031,成都;2.西南交通大学牵引动力国家重点实验室超导技术研究所,610031,成都//第一作者,硕士研究生)
基于分子电流环模型,利用毕奥·萨伐尔定律建立了能够实现单块永磁体磁感应强度分布的三维模型;通过坐标变换的方法,得到可描述任意大小永磁体组合的磁感应强度分布的模型。以Halbach型永磁轨道作为研究对象,建立了完整的三维计算模型。通过对比分析,得到磁感应强度的解析解、实测值以及有限元解的一致性结果,肯定了模型的正确性。
永磁轨道;磁感应强度;三维计算模型
AbstractBased on the molecular current cycle model,a 3D numerical model is built to describe the magnetic field distribution of a single permanent magnet by using Biot-Savart Law.Then,through coordinate transformation,a model to describe the magnetic field distribution for any sizes of permanent magnets and any combinations is obtained.According to the Halbach type track,a complete 3D numerical model is built,and correctional parameters are introduced into the model by comparison and analysis.The correctness of the model is further verified by the measured data and finite element simulation results.
Key wordspermanent magnet track; magnetic field distribution;3D numerical model
First-author′s address Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province,Southwest Jiaotong University,610031,Chengdu,China
高温超导磁浮系统具有稳定、经济、环保等优点,在城市轨道交通领域具有很大的发展潜力。目前,针对该系统的重要组成部分永磁轨道的研究方法主要采用有限元法、实验测试法以及二维解析法。其中,有限元法较为精确,但由于计算量大,不适合对大型轨道进行计算;实验测试法成本较高;二维解析法假设轨道磁场沿一个方向完全均匀,无法描述存在缺陷或磁场分布不均匀的轨道。故在计算大型轨道结构时,需要寻求一种计算量更小、更经济的方法以提高效率。
本文根据毕奥·萨伐尔定律,利用分子电流环模型[1]建立了可求解单块永磁体磁感应强度的三维计算模型。此外,利用坐标变换的方法简化了计算流程。在此基础上建立了完整的Halbach型永磁轨道磁感应强度计算模型,通过对该模型的解析解、实测值以及ANSYS Maxwell二维有限元解进行对比,验证了该模型的正确性。
1 永磁体磁感应强度表达式
1.1 单块永磁体建模
根据毕奥·萨伐尔定律有:

式中:
d B ——磁感应强度微量,T;
I——源电流,A/m2;
r ——电流源指向待求场点的矢量,m;
I d l——源电流的微小线元,A/m;
μ0——真空磁导率,其值为4π×10-7H/m。式中,d B的方向垂直于I d l与r所确定的平面(符合右手螺旋定则)。
图1为长方体永磁体示意图。该永磁体长为a,宽为b1-b0,高为h。由图1可知,永磁体表面任意点P1(x1,y1,z1)(以微面ABDC上一点为例)处源电流在空间任意一点 P(x,y,z)处产生的磁感应强度可表示为:

式(3)中,x1,j代表微面 ABDC 上某点的 x 坐标值;z1,j代表微面ABDC上某点的z坐标值。

图1 长方体永磁体示意图
同理可得,微面ABHG、HGEF及EFDC上的电流在任意点 P(x,y,z)处的磁感应强度 d Bxi、d Byi、d Bzi(i=2,3,4)。为简化表达式,引入以下记号及函数表达式[2]。经过积分计算,可得图1中永磁体x,y,z方向的磁感应强度:
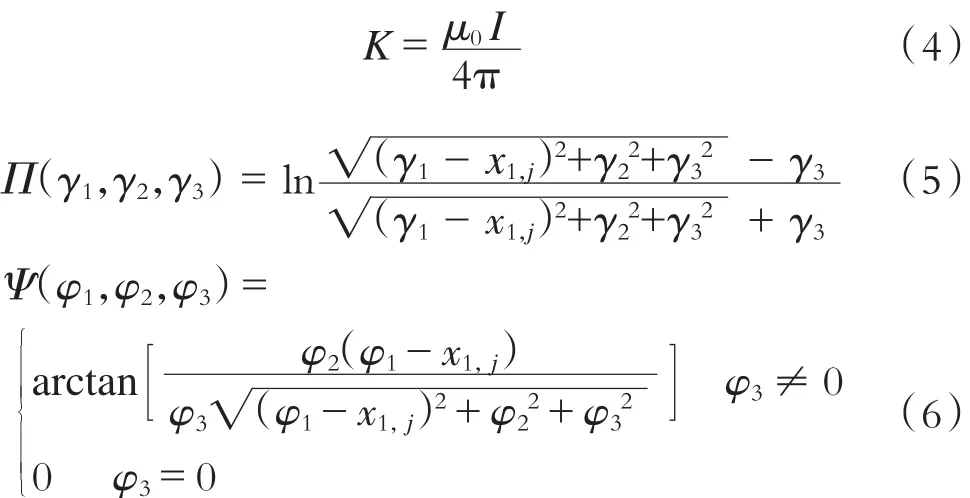


1.2 Halbach型永磁轨道建模
不同磁化方向、不同位置及尺寸的永磁体,可通过坐标变换得到其磁感应强度。本文以西南交大牵引动力国家重点实验室高温超导磁悬浮环形试验线所选用的Halbach型轨道(以下简称“试验轨道”)为例进行计算。试验轨道结构如图2所示,图中箭头为各单块永磁体的磁化方向。
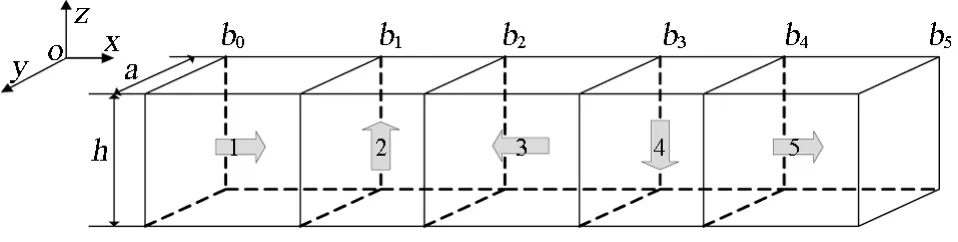
图2 试验轨道结构示意图
由图2可知,试验轨道在轨道截面上由5块永磁体组成,永磁体编号从左到右分别为1、2、3、4、5号。设各块永磁体x,y,z方向的磁感应强度分别为Bxk、Byk及 Bz(kk=1,2,3,4,5)。 其中,1 号永磁体即为图1所示永磁体,5号永磁体可由1号永磁体平移得到,3号永磁体可由1号永磁体经过坐标对称得到[3],2号和4号永磁体可由1号永磁体经过坐标旋转得到。永磁体尺寸不同时,只需带入不同的a,b,h值即可。对各永磁体的磁感应强度求和,得到Halbach型轨道的磁感应强度为:

计算中所需的电流,可由以下2种方法得到。方法1:针对已知磁感应强度的永磁体可直接给出电流I;方法2:确保模型正确时,可测得空间中任意一点的磁感应强度,将其代入式中可反推出电流I。本文采用上述方法2来计算电流。
本文建模实质是对各单块永磁体的磁感应强度进行矢量叠加,由于忽略了各永磁体的相互作用对磁感应强度的影响,势必会导致误差。因此,本文引入修正参数 η,修正后的Bz′如式(12)所示。
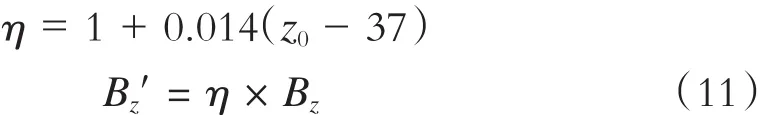
式中:
z0——以轨道上表面为零点的垂向位置。
2 结果分析
2.1 解析解与实测值对比
由图2可知,所有永磁体的磁化方向均垂直于y方向。由图1可知,该轨道磁感应强度分量By沿y=平面两侧对称分布。对于沿y方向延伸足够长的轨道,其磁感应强度分量By=0。故只需求解磁感应强度的分量Bx和Bz。图2所示试验轨道尺寸及电流参数如表1所示。

表1 试验轨道尺寸及电流参数表
本文采用Hall Generator 3020型高斯计来测量试验轨道的磁感应强度。于磁极处测得一组法向磁感应强度Bz随z的变化数据,并与解析解作对比,结果如图3所示。由图3可知,Bz的解析解与实测值一致性较高。
图4为试验轨道横截面方向法向磁感应强度Bz的解析解与实测值对比图。鉴于试验轨道磁场沿中轴线呈对称分布[4],本文只测量(计算)并对比了轨道的左半部分。由图4可知,解析解与实测值有较高的吻合度。值得注意的是,轨道边缘处的解析解的绝对值要小于实测值。
2.2 解析解与有限元解对比
为进一步验证模型,采用ANSYS Maxwell建立了试验轨道的二维模型。矫顽力在该模型中取994 000 A/m,在解析解中I取1.09×105A/m3,其他参数与表1保持一致。试验轨道法向磁感应强度Bz、切向磁感应强度Bx的解析解与有限元解的对比图如图5、图6所示。
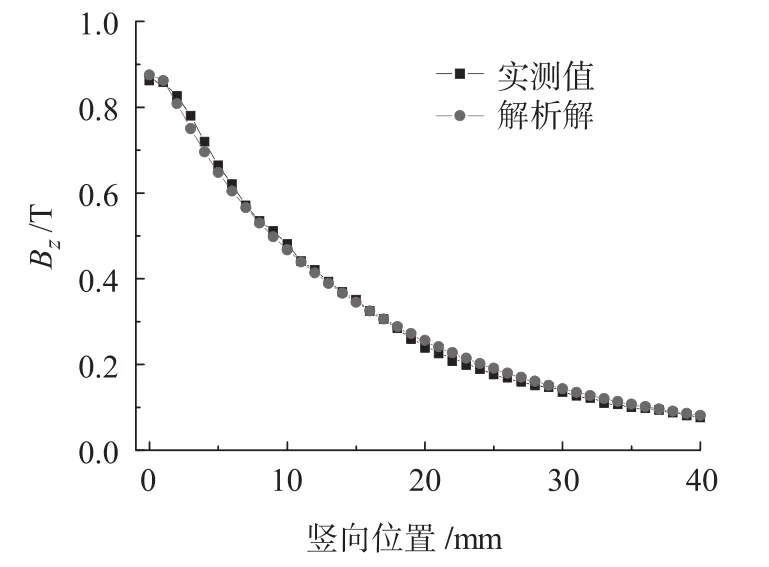
图3 磁极处法向磁感应强度Bz解析解与实测值对比图

图4 试验轨道截面方向法向磁感应强度Bz解析解与实测值对比图
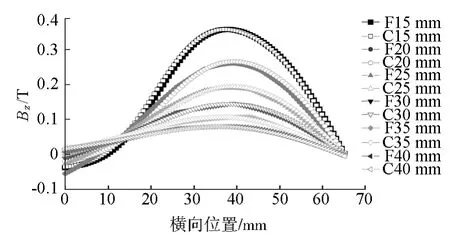
图5 试验轨道法向磁感应强度Bz的解析解与有限元解对比图
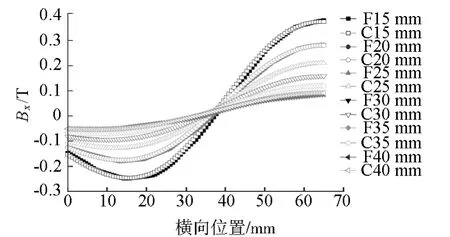
图6 试验轨道切向磁感应强度Bx的解析解与有限元解对比图
由图5可知,两者的吻合度整体较高。在试验轨道边缘处,两者有一定的差距,解析解略小于有限元解。这说明忽略各永磁体之间的相互影响将会导致误差,并且在轨道表面附近表现更为明显。由图6可知,两者吻合度亦较高,在试验轨道边缘处以及距离轨道表面较近处未出现明显的差距。
2.3 误差分析
观察对比结果,磁极上方法向磁感应强度解析解与实测值误差为2.5%;试验轨道截面方向法向磁感应强度的解析解与实测值误差为13.2%(若不包含左侧轨道边缘处的10个点,则误差为5.5%);试验轨道截面方向法向磁感应强度的解析解与有限元解误差为9.5%(若不包含左侧轨道边缘处的10个点,则误差为2.6%);轨道切向磁感应强度的解析解与有限元解误差为0.39%。法向磁感应强度的解析解、实测值与有限元解对比均存在一定的误差。这是由于计算解析解的过程中忽略了永磁体相互之间的磁力线挤压作用;解析解与实测值的误差大于解析解与有限元解的误差,这是由于试验轨道是由小块永磁体拼接而成,而每一块永磁体的性能均可能存在差异;试验轨道边缘处三个解的误差较中心处较大,这是由于解析解忽略了试验轨道的边缘效应。试验轨道截面方向的切向磁感应强度与有限元解相似度较高。
3 结语
本文利用分子电流环模型,建立了单块永磁体模型,并通过坐标变换的方法得到了完整的Halbach型永磁轨道模型。计算磁感应强度时,由于忽略了各永磁体之间的影响,在试验轨道边缘处存在一定的误差。在与实测结果比对后,引入了修正参数。修正后的解析解与实测值以及 ANSYS Maxwell有限元解均有较高的吻合度。切向的磁感应强度Bx的计算中,解析解与有限元法解吻合度较高。在环形试验线车体振动范围以及运行速度内,该模型计算可以满足精度要求。
[1]CAMPBELL P,CHARI M V K,D′ANGELO J.Threedimensional finite element solution of permanent magnet machines[J].Magnetics IEEE Transactions on,1981,17(6):2997-2999.
[2]GOU X,YANG Y,ZHENG X.Analytic expression of magnetic field distribution of rectangular permanent magnets[J].Applied Mathematics and Mechanics,2004,25(3):297-306.
[3]MA G,LIU H,WANG J,et al.3D modeling permanent magnet guideway for high temperature superconducting maglev vehicle application[J].Journal of superconductivity and novel magnetism,2009,22(8):841-847.
[4]JING H,WANG J,WANG S,et al.A two-pole halbach permanent magnet guideway for high temperature superconducting,maglev vehicle[J].Physica C Superconductivity&Its Applications,2007,463:426-430.
[5]KAMERLINGH-ONNES H.On the sudden change in the rate at which the resistance of mercury disappears[J].Comm Phys Lab Univ Leiden,1911:124.
[6]WU M K,ASHBURN J R,TORNG C J,et al. Superconductivity at 93 K in a new mixed-phase Y-Ba-Cu-O compound system at ambient pressure[J].Physical Review Letters,1987,58(9): 908.
[7]邓自刚,王家素,王素玉,等.高温超导飞轮储能技术发展现状[J].电工技术学报,2008,12:1-10.
[8]WANG J,WANG S,ZENG Y,et al.The first man-loading high temperature superconducting maglev test vehicle in the world[J].Physica C Superconductivity&Its Applications,2002,378:809-814.
[9]SCHULTZ L,HAAS O,VERGES P,et al.Superconductively levitated transport system-the Supra Trans project[J].IEEE Transactions on Applied Superconductivity,2005,15 (2):2301-2305.
[10]任仲友.永磁导轨上高温超导磁悬浮的实验研究与数值计算[D].成都:西南交通大学,2004.
[11]芦逸云.永磁轨道上方高温超导块材磁悬浮实验与仿真研究[D].成都:西南交通大学,2009.
Calculation of the Magnetic Field Distribution of Permanent Magnet Track
LIHaitao,GE Yumei,SUN Ruixue,DENG Zigang
TM153+.1:U237
10.16037/j.1007-869x.2017.09.005
2015-11-18)
*国家自然科学基金项目(51375404)

