不同牵引策略下地铁杂散电流动态分布研究

张栋梁 刘颖熙 吴 晗

不同牵引策略下地铁杂散电流动态分布研究

张栋梁 刘颖熙 吴 晗

（中国矿业大学电气与动力工程学院，221116，徐州//第一作者，副教授）

基于3种经典牵引策略思想，建立了不同牵引策略下的列车牵引模型。将回流系统等效为4层结构的平面分布参数电阻网络，建立了地铁杂散电流分布模型。通过牵引供电等效计算，将不同牵引策略下的列车牵引模型与杂散电流分布模型相结合，构建了动态边界条件，得到了不同牵引策略下的杂散电流动态分布模型。在所建立的杂散电流动态分布模型的基础上，提出一种杂散电流泄漏总量的计算方法。利用MATLAB软件，对不同牵引策略下的杂散电流动态分布模型进行仿真研究，可为杂散电流的腐蚀防护提供一定的理论参考。

地铁；杂散电流动态分布；牵引策略；牵引供电

AbstractAccording to 3 classical traction strategies，corresponding train traction models are introduced.In this paper，a stray current distribution model is established，in which the reflow system is equivalent to plane distributed parameter resistor network in a four-layer structure.Through equivalent calculation of the traction power supply，the train traction models under different traction strategies are integrated with the stray current distribution models to build dynamic boundary conditions，thus the stray current dynamic distribution models under different traction strategies are obtained.Meanwhile,based on the distribution models，a method to calculate the total amount of stray current leakage is proposed.Then,MATLAB software is used to simulate the stray current dynamic distribution models under different traction strategies，the result could provide a theoretical reference for the stray current corrosion protection.

Key wordsmetro； dynamic distribution of stray current；traction strategy；traction power supply

Author′s addressSchool of Electrical and Power Engineering，China University of Mining and Technology，221116，Xuzhou，China

地铁杂散电流来源于列车牵引电流，而列车牵引电流主要受列车牵引策略影响。因此，研究不同牵引策略下的杂散电流动态分布情况对杂散电流的腐蚀防护具有一定的理论指导意义和实际应用价值。

列车牵引策略繁多，其中比较经典的有快速牵引策略、经济牵引策略及舒适牵引策略［1］。

目前，许多学者将列车牵引引入到杂散电流分布规律的研究中时，并没有考虑列车不同牵引策略对杂散电流动态分布的影响［2-4］。本文基于上述3种牵引策略，建立了3种相应的牵引计算模型，同时将复杂的杂散电流空间电流场问题简化为平面分布参数电阻网络问题，建立了4层结构杂散电流分布模型。并通过列车牵引供电计算，将牵引计算模型与杂散电流分布模型相结合，得到3种牵引策略下的杂散电流动态分布模型。

1 牵引计算建模

基于上述3种牵引策略，建立了3种相应的牵引计算模型。牵引计算模型相关参数主要以文献［5］为基础，假设列车在平直轨道上运行，运行区间位于两变电所之间。列车运行阻力只考虑基本阻力，列车采用再生制动方式，所回馈的能量能被接触网全部吸收。采用单质点模型对列车进行受力分析，根据微元思想将运行过程分段线性化，认为在Δt时间内列车受力恒定。

1.1 快速牵引计算模型

（1）加速运行阶段（列车速度v＜列车限速值vlim）。此阶段列车运行的主要参数求解见式（1）。

式中：

Ti——列车牵引力，kN；

Ri——列车运行基本阻力，kN；

ai——列车加速度，m/s2；

vi——列车速度，km/h；

Si——列车行走距离，m；

Pi——列车牵引功率，kW；

Δt——计算步长，s；

M——列车质量，t；

γ——回转质量系数。

列车运行基本阻力Ri采用Davis经验公式计算：

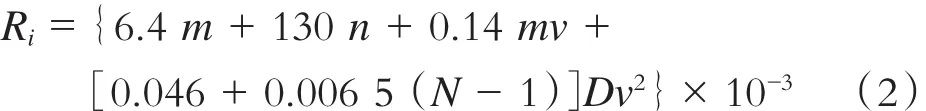
式中：

n——列车车轴数，个；

m——列车车辆数，辆；

D——列车前端面积，m2。

（2）匀速运行阶段（v=vlim）。此阶段列车加速度和牵引功率分别为：

（3）制动运行阶段。此阶段列车的主要参数求解与加速运行阶段类似；不同之处在于牵引力变成了制动力，且反向作用于列车。

1.2 经济牵引计算模型

加速运行阶段（v＜列车经济速度veco）、匀速运行阶段（v=veco）与制动运行阶段列车运行主要参数的求解和快速牵引计算模型相同。但在经济牵引策略下，列车匀速运行和制动运行之间有一段惰性运行过程。惰性运行时列车加速度和牵引功率分别为：

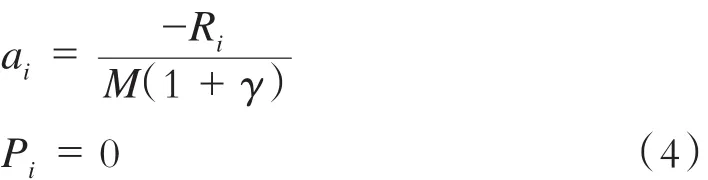
1.3 舒适牵引计算模型

（1）加速运行阶段（v＜veco）。此阶段列车加速度和牵引功率分别为：

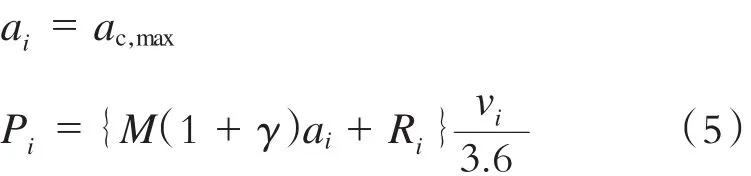
式中：

ac，max——乘客舒适级别最大加速度，m/s2。

（2）匀速运行阶段（v=veco）。此阶段列车运行主要参数的求解与快速牵引计算模型计算的匀速运行阶段相同。

（3）制动运行阶段。此阶段列车加速度和牵引功率分别为：

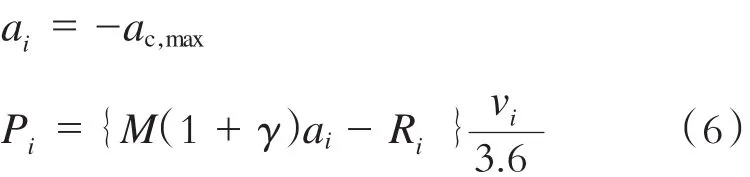
以上3种牵引计算模型均通过反向递推的方法确定出在当前速度下列车所需的最短制动距离。一旦进入制动距离范围，列车立即制动减速运行，否则保持当前状态运行。

2 地铁杂散电流动态分布建模

2.1 列车牵引供电等效模型

将列车等效为理想电流源，区间两端变电所视为理想电压源。从供电的角度来看，绝大部分牵引电流经由钢轨回流到变电所。因此，本文在牵引供电等效上，只考虑接触网电阻和钢轨电阻。列车牵引供电等效模型图如图1所示。由图1可知，当列车位于S处时，由基尔霍夫定律及列车牵引功率可得：

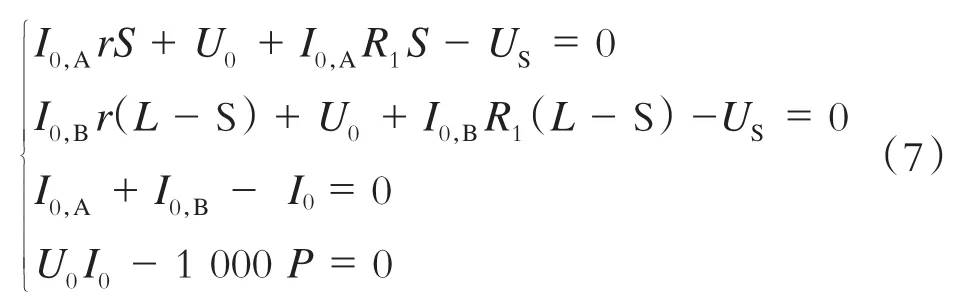
式中：

I0，A——变电所A电流；

I0，B——变电所B电流；

US——变电所电压；

I0——列车电流；

U0——列车电压；

P——列车牵引功率；

S——列车运行距离；

L——列车运行区间长度；

r——接触网电阻；

R1——钢轨电阻。

由式（7）得：

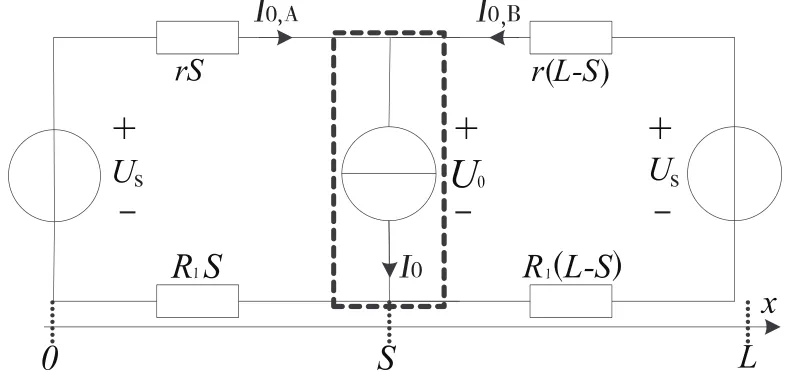
图1 列车牵引供电等效模型图

2.2 杂散电流动态分布模型

将地铁回流系统简化为平面分布参数电阻网络，并假设：①钢轨电阻和钢轨对排流网过渡电导均匀分布；②排流网电阻和排流网对埋地金属过渡电导均匀分布；③埋地金属电阻和埋地金属对大地过渡电导均匀分布。

在假设的基础上建立“钢轨-排流网-埋地金属-大地”4层结构形式的回流系统模型，如图2所示。

图2 回流系统模型图

沿列车运行方向，在微元Δx上构建等效电阻网络，如图3所示。

图3 微元Δx等效电阻网络

根据图2和图3，分析各电压电流之间的关系，可建立如下杂散电流分布模型：

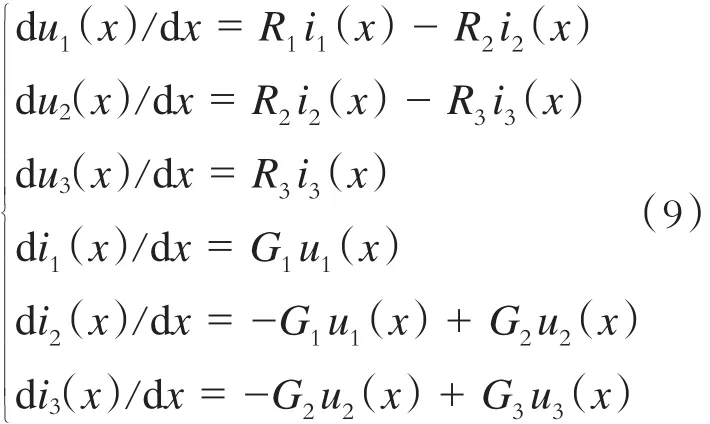
令

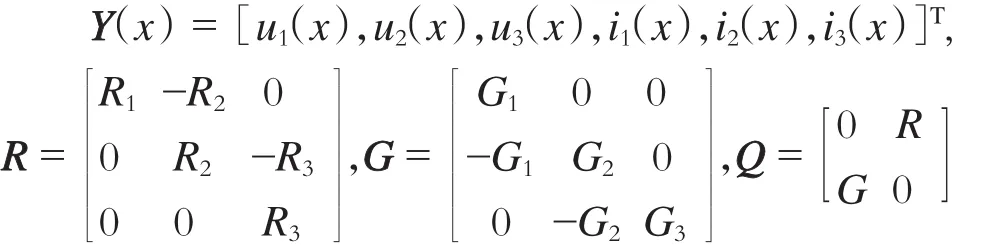
则式（9）可转化为：

求解式（10），得通解为：

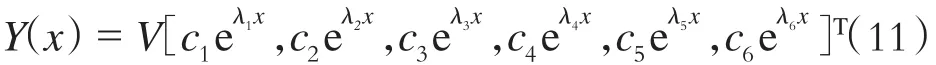
其中，λ1、λ2、λ3、λ4、λ5、λ6为 Q 的特征值，C1、C2、C3、C4、C5、C6为待定系数。

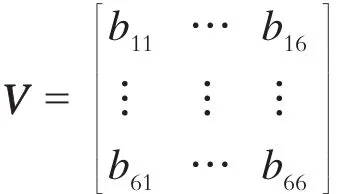
令待定系数矩阵 C=［C1、C2、C3、C4、C5、C6］T，V为Q的特征向量矩阵：

以列车位置S处作为分界点，将回流系统电阻网络划为两个分析域（0～S和S～L）。

当列车处于0～S分析域内时，设

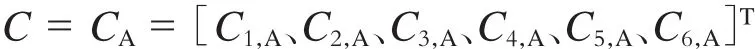
根据变电所电流可构建如下边界条件：

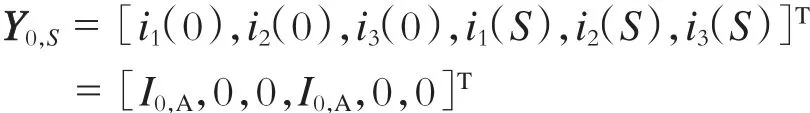
即：

令

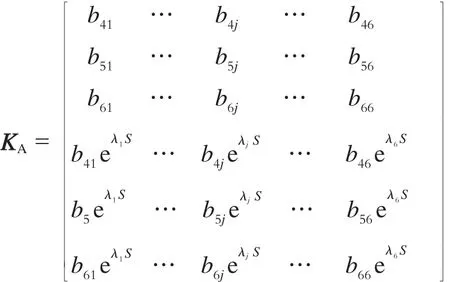
则式（12）可转化为：

求出KA的广义逆矩阵KA+，则待求系数矩阵为：

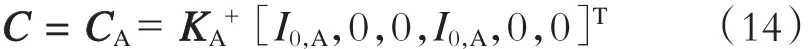
将待定系数代入式（11），即可求解出列车处于0～S分析域内的杂散电流分布模型。

当列车处于S～L分析域内时，边界条件为：

同理可得：

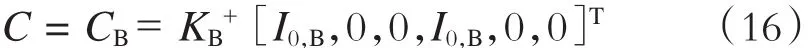
则待定系数矩阵为：将待定系数代入式（11），即可求解出列车处于S～L分析域内的杂散电流分布模型。

根据杂散电流定义，列车运行区间内杂散电流为：

式中：

I——变电所电流，当列车处于0～S分析域内时，I=I0，A； 当列车处于 S～L 分析域内时，I=I0，B。则区间钢轨电位为：

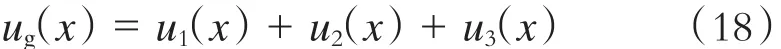
将列车牵引供电等效模型与杂散电流分布模型相结合，构建动态的边界条件 Y0，S和 YS，L，即可得到不同牵引策略下的杂散电流动态分布模型。

2.3 杂散电流泄漏总量的计算方法

根据CJJ 49—92《地铁杂散电流腐蚀防护技术规程》规定，地铁结构与设备受杂散电流腐蚀的危险性直接定量指标为杂散电流密度。本文依据所建立的杂散电流动态分布模型以及杂散电流腐蚀的累积效应，将杂散电流腐蚀危险性的评价指标等效转化为列车从变电所A运行到变电所B过程中区间杂散电流泄漏总量，即：

式中：

I0，A，x——列车运行至x处变电所A电流，A；

ug，x——变电所A处的钢轨电位，V。

IS的计算精度受步长Δt影响。另外，钢轨电位亦能反映杂散电流泄漏强度的电气量。因此，本文以列车运行过程中区间杂散电流泄漏总量IS和区间钢轨电位最大幅值ug，max来评价杂散电流腐蚀的危险性。

3 仿真分析

根据上述建立的不同牵引策略下的杂散电流动态分布模型，利用MATLAB软件进行仿真计算，研究分析不同牵引策略对杂散电流动态分布的影响。

（1）仿真参数。取 L=1.5 km，Δt=1 s，M=300 t，γ =0.06，vlim=80km/h，veco=60 km/h，ac，max=0.63m/s2，n=24，N=6，D=10m2，US=1500V，r=0.026 Ω/km；R1=0.030Ω/km，R2=0.010Ω/km，R3=0.020Ω/km，G1=0.333 S/km，G2=0.500 S/km，G3=0.500 S/km。

（2）列车牵引供电等效模型仿真结果。3种牵引策略下列车牵引功率P以及区间两端变电所电流I0，A及I0，B的仿真曲线如图4～6所示。不同运行阶段的列车牵引功率与区间两端变电所电流最大值如表1所示。由图4～6及表1可知，快速牵引策略下列车运行历时最短（90 s），经济牵引策略下历时适中（110 s），舒适牵引策略下历时最长（118 s）。 列车牵引功率和变电所电流在快速牵引策略下运行时间较长，在舒适牵引策略下运行时间较少。经济牵引策略下列车在惰行阶段的牵引功率和变电所电流均为零；在其他运行阶段列车牵引功率和变电所A电流介于另外两种牵引策略之间，变电所B电流小于另外两种牵引策略。此外，3种牵引策略下列车牵引电流主要由变电所A提供，再生制动回馈电流主要被变电所B吸收。

表1 不同运行阶段的列车牵引功率和区间两端变电所电流最大值

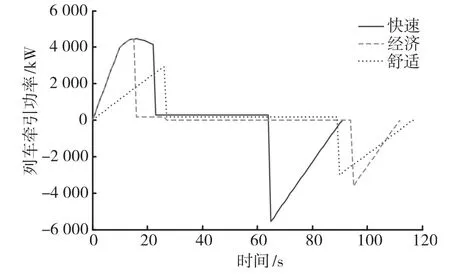
图4 列车牵引功率曲线

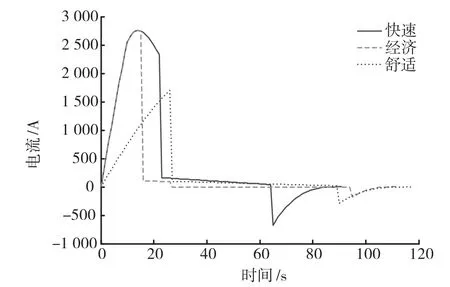
图5 变电所A电流曲线

图6 变电所B电流曲线

（3）杂散电流动态分布模型仿真结果。3种牵引策略下杂散电流三维动态分布图及俯视图如图7所示。由图7可知，经济牵引策略下的杂散电流明显小于另外两种牵引策略；快速牵引策略下的杂散电流最大。由区间位置可知，3种牵引策略下的杂散电流的较大位置均位于区间中部附近；由运行时刻可知，3种牵引策略下的杂散电流较大时刻均出现在加速运行阶段末期以及制动运行阶段初期。

图7 杂散电流三维动态分布图及其俯视图

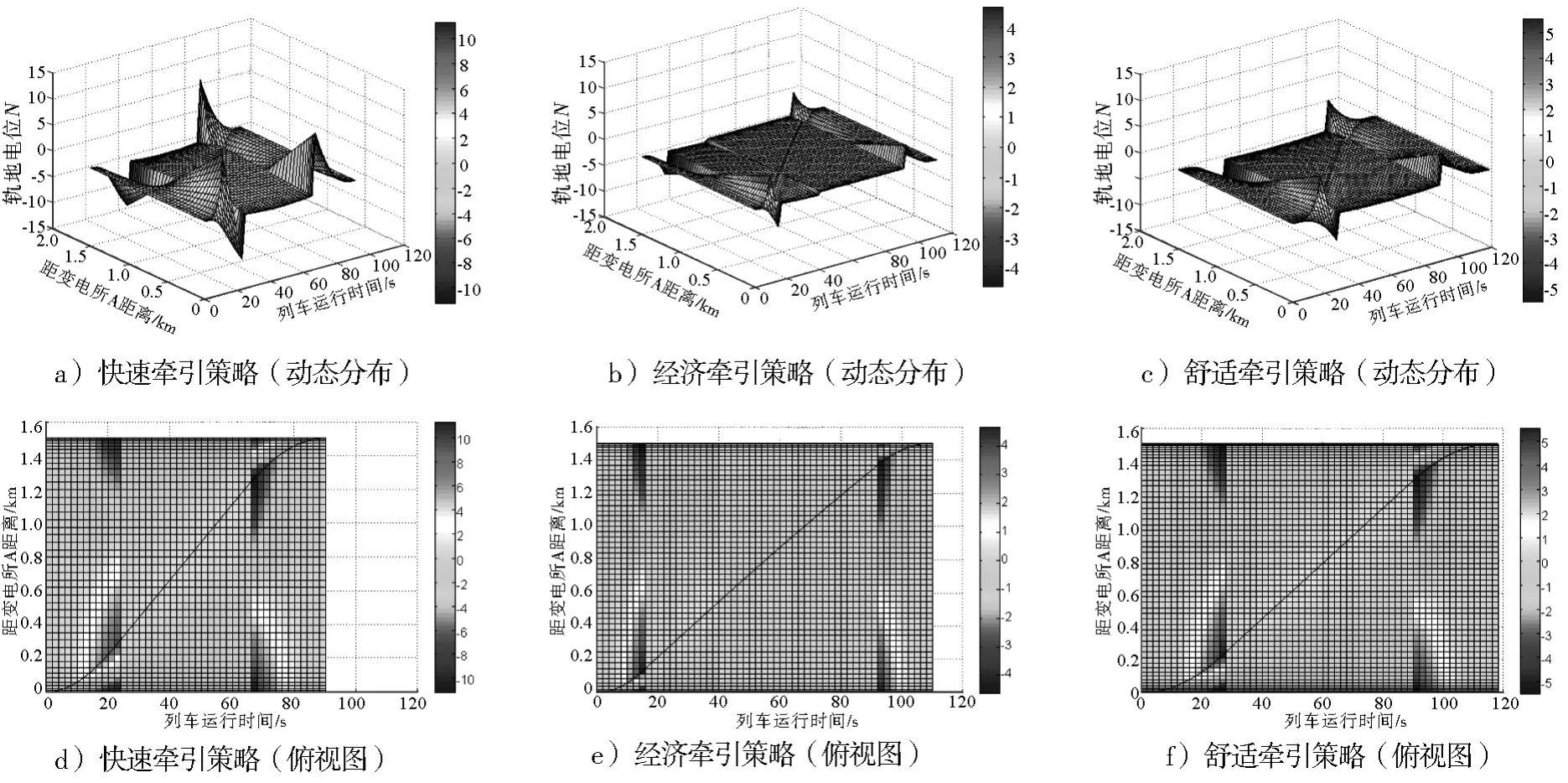
图8 钢轨电位三维动态分布图及俯视图

图8 为3种牵引策略下钢轨电位三维动态分布图及俯视图。由图8可知，经济牵引策略下钢轨电位幅值明显低于另外两种牵引策略，快速牵引策略下钢轨电位幅值最高。从区间位置来看，3种牵引策略下钢轨电位幅值较高的位置均位于区间两端变电所回流点附近以及列车所在位置附近；从运行时刻来看，3种牵引策略下钢轨电位幅值较高的时刻均出现在加速运行阶段末期以及制动运行阶段初期。

由不同牵引策略下杂散电流和钢轨电位评价指标（如表2）可知：快速牵引策略下杂散电流泄漏总量最大；舒适牵引策略下杂散电流泄漏总量较小，为快速牵引策略下的57.85%；经济牵引策略下杂散电流泄漏总量最小，仅是快速牵引策略下的27.51%。同时，快速牵引策略下钢轨电位的最大幅值亦是最大；舒适牵引策略下钢轨电位的最大幅值较小，为快速牵引策略下的49.11%；经济牵引策略下钢轨电位的最大幅值最小，为快速牵引策略下的40.20%。

表2 不同牵引策略下杂散电流和钢轨电位评价指标值

4 结论

本文基于3种经典牵引策略建立了不同牵引策略下杂散电流的动态分布模型，同时利用MATLAB软件，对杂散电流动态分布模型进行了仿真分析，相关结论如下：

（1）本文所建立的杂散电流动态分布模型能够直观地反映列车在不同牵引策略下各个运行阶段的杂散电流和钢轨电位动态分布情况。

（2）基于所建立的杂散电流动态分布模型，提出了一种列车运行时区间杂散电流泄漏总量的计算方法。该方法能有效地计算和评价列车在不同牵引策略运行过程中杂散电流的泄漏量和腐蚀危险性。

（3）列车在3种不同的牵引策略下的运行过程中，均为加速阶段及制动阶段的杂散电流较大、钢轨电位幅值较高，且杂散电流较大的位置位于线路区间中部，钢轨电位幅值较高的位置位于列车处及两端变电所附近。因此，从回流系统的角度出发，应加强两端变电所附近加速区段和制动区段的杂散电流腐蚀防护。

（4）列车在经济牵引策略下运行时，与另外两种牵引策略相比，杂散电流泄漏总量最少，钢轨电位最大幅值最小。因此，从列车牵引运行策略的角度出发，为减小杂散电流的腐蚀危害，列车宜采用经济牵引策略运行。

［1］孟建军，陈晓强，胥如迅，等.基于多质点的城轨列车牵引计算分析与仿真［J］.系统仿真学报，2015，27（3）：603-608，619.

［2］XU S，LI W，WANG Y.Effects of vehicle running mode on rail potential and stray current in DC mass transit systems［J］.IEEE Transactions on Vehicular Technology，2013，62（8）：3569-3580.

［3］FOTOUHI R，FARSHAD S，FAZEL S S.A new novel DCbooster circuit to reduce stray current and rail potential in DC railways［C］//IEEE.International Conference-workshop on Compatibility and Power Electronics.6th.Badajoz： IEEE，2009：457-462.

［4］王崇林，马草原，王智，等.地铁直流牵引供电系统杂散电流分析［J］.城市轨道交通研究，2007，10（3）：51-53，56.

［5］石红国，彭其渊，郭寒英.城市轨道交通牵引计算模型［J］.交通运输工程学报，2005，5（4）：20-26.

［6］吴仲刘，阳光武.基于ANSYS的地铁车辆振动特性分析［J］.科学技术与工程，2012，27：7130-7133，7137.

［7］JIA Z，YANG Z，LIN F，et al.Dynamic simulation of the DC traction]ower system considering energy storage devices［J］.Transportation Electrification Asia-Pacific，2014.

［8］陈志光，秦朝葵，唐继旭.城市轨道交通动态杂散电流理论分析与计算［J］.城市轨道交通研究，2014（3）：24.

［9］李群湛.城市轨道交通交流牵引供电系统及其关键技术[J].西南交通大学学报，2015（2）：199-207.

Dynamic Distribution of Metro Stray Current under Different Traction Strategies

ZHANG Dongliang，LIU Yingxi，WU Han

U223.6+2

10.16037/j.1007-869x.2017.09.007

2016-01-14）