递归算法在单一矩形毛坯无约束最优排样中的应用
李海生
(广西民族师范学院 物理与电子工程学院, 广西 崇左 532200)
递归算法在单一矩形毛坯无约束最优排样中的应用
李海生
(广西民族师范学院 物理与电子工程学院, 广西 崇左 532200)
优化排样问题属于典型的非确定型NP问题,需要借助计算机辅助排样选出材料利用率最大化和排样下料效率最高的排样方案,以解决企业对排样的实际需求。讨论了单一矩形毛坯无约束剪切排样优化处理问题,基于剪切冲裁相结合的下料工艺、以条带数衡量排样方式的复杂性,应用递归算法通过枚举搜索法遍历所有可能的更优的排样方案,在保证毛坯数最优的前提下选出条带数最少的排样方案。实验计算结果表明所述算法有效。
计算机辅助;递归算法;优化排样;矩形毛坯
Abstract: Optimal layout problem is a typical non-deterministic NP problem that needs the help of Computer Aided Nesting to select the layout scheme with material utilization ratio maximization and cutting patterns efficiency highest. In order to solve the actual demand of enterprise to the layout, the optimization problem of unconstrained cutting patterns for single rectangular blank is discussed. Through the two stages of cutting and blanking stock, with the complexity of cutting patterns measured by the number of strips, using a recursive algorithm search by enumeration method to traverse layout for all possible better, on the premise of guarantee blank for optimal, we choose the layout scheme of the minimum number strip. The calculation results show that the algorithm is effective.
Keywords: computer-aided; recursive algorithm; optimal layout; rectangle blanks
优化排样问题属于典型的非确定型NP问题[1],传统的人工排样受到多方面因素的影响和制约,降低了生产效率,增加了成产成本。因此,应用计算机辅助排样(computer aidde nesting,CAN)来解决实际排样问题是生产力发展的需要[2],可充分利用计算机的高速和精确的运算能力以及计算机编程技术,在短时间内遍历所有可能的更优的排样方案,选出材料利用率最大化和排样下料效率最高的排样方案,以达到降低材料成本和排样下料环节劳动成本的目的。
随着计算机技术的发展和深入应用,计算机辅助排样软件[3]得到了较好地发展和应用。由于单一矩形毛坯排样可以灵活组织下料,同时具有极大的通用性,在涉及到材料切割排样的行业中具有现实应用需求,因此深入研究单一矩形毛坯排样问题具有重要价值。对于单一矩形毛坯排样问题的求解,文献[4~5]提出的算法能实现毛坯数最优,但没有考虑切割工艺的复杂性问题;文献[6]提出的算法能减少条带数,但不能保证条带数最优;文献[7]提出的算法能实现毛坯数和切割工艺最优,但算法复杂。本文应用递归算法对单一矩形毛坯在矩形板材上进行无约束[8]优化排样,基于规范多级方式转换定理[9],以条带数衡量单一矩形毛坯剪切排样方式切割工艺的复杂性,通过枚举法搜索在实现毛坯数最优的前提下生成条带数最优的排样方式,同时算法具有简单、易于实现软件开发的优点。
1 递归的基本设计思想
基于剪冲工艺的下料方式,在剪切阶段每一刀将从当前尺寸为x×y的板材中切出一根条带(条带的宽度为毛坯的长度l,其尺寸为x×l或y×l),依此处理方式直到剩余板材不能切出一个毛坯为止。依次考察当前板材及其相应的剩余板材(从当前板材切出一根条带后其尺寸为x×(y-l)或(x-l)×y)的排样方式,发现具有如下特征:
① 从排样问题的求解规模来看,剩余板材的尺寸相对于当前板材的尺寸小,可知剩余板材排样问题的计算求解规模相对于当前板材来说其计算求解规模更小。
② 从排样问题的求解性质来看,当前板材和剩余板材的求解性质是相同的,都是在保证毛坯数最大化的前提下生成条带数最少的排样方式。
③ 从板材所有可能的尺寸来看,在剪切过程中每一刀剪切出一根竖直条带或垂直条带,可见对于两两相邻的板材来说具有非常紧密的联系,在尺寸上后一个板材的输入是前一个板材的输出,因此前一个板材的解依赖于后一个板材的解。
④ 从板材的整个剪切阶段来看,所有一系列剩余板材的问题求解规模和尺寸都是按照一定的条件有规律地递减,从而使整个单一矩形毛坯无约束排样问题逐渐趋向于结束而得到直接解。当剩余板材不能再剪切出任何一个毛坯时,那么当前排样方式的求解过程结束。
综合①~④来看,单一尺寸矩形毛坯排样问题的求解过程具有递归需要的递推前进段、回退返回段和边界条件,满足递归求解排样问题的条件。对于两两相邻的板材,后一个板材的排样问题是前一个板材排样问题的子问题,对所有可能尺寸的板材可应用递归算法[10]进行求解。通过搜索遍历所有的递归排样分支,即可找到毛坯数最优和条带数最优的规范多级排样方式。
2 递归剪切排样算法设计
设毛坯尺寸为l×w(l>w,l为毛坯长度,w为毛坯宽度),板材初始尺寸为L×W(L>W,L为板材长度,W为板材宽度)。对于尺寸为x×y的当前板材,令M(x,y)和N(x,y)分别表示从当前板材剪切出的条带数量和从条带冲裁出的毛坯数量。令D(x,y)用于记录从当前板材x×y剪切出第1根条带的切割方向。令M0(x,y)和N0(x,y)分别表示当前板材x×y其最优排样方式剪切出的条带数量和从条带冲裁出的毛坯数量。令Mx和Nx分别表示对当前板材x×y进行横切时,对应的递归排样分支剪切出的条带数和所含毛坯数。令My和Ny分别表示对当前板材x×y进行竖切时,对应的递归排样分支剪切出的条带数和所含毛坯数。令M(L,W)和N(L,W)分别表示当前排样方式剪切出的条带数和冲裁出的毛坯数。一维数组D用来记录当前排样方式中所含条带的切割方向。M0(L,W)和N0(L,W)表示当前最优排样方切割出的条带数量和从条带冲裁出的毛坯数量。一维数组D0记录当前最好排样方式各根条带的剪切方向。
2.1 递归的方程式
基于规范多级排样方式,从当前板材(x,y)剪切出条带,每一刀剪切方向只能是横切或竖切。
1) 横切
如图1所示,从当前板材的上边剪切出1根X向条带,条带的尺寸是x×l,令条带x×l可以冲裁出的毛坯数用Num(x) 表示,则有Num(x)=int(x/w)。剪切出1根X向条带后剩余板材的尺寸是x×(y-l),令其可以剪切出的毛坯数量为N(x,y-l),条带数为M(x,y-l)。令D(x,y)=0表示当前板材x×y第1刀的切割方向为竖切。按此切割方式,可得到如下关系式:
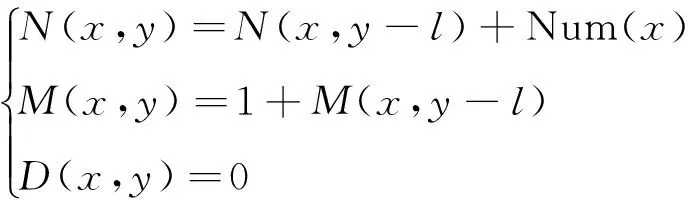
(1)
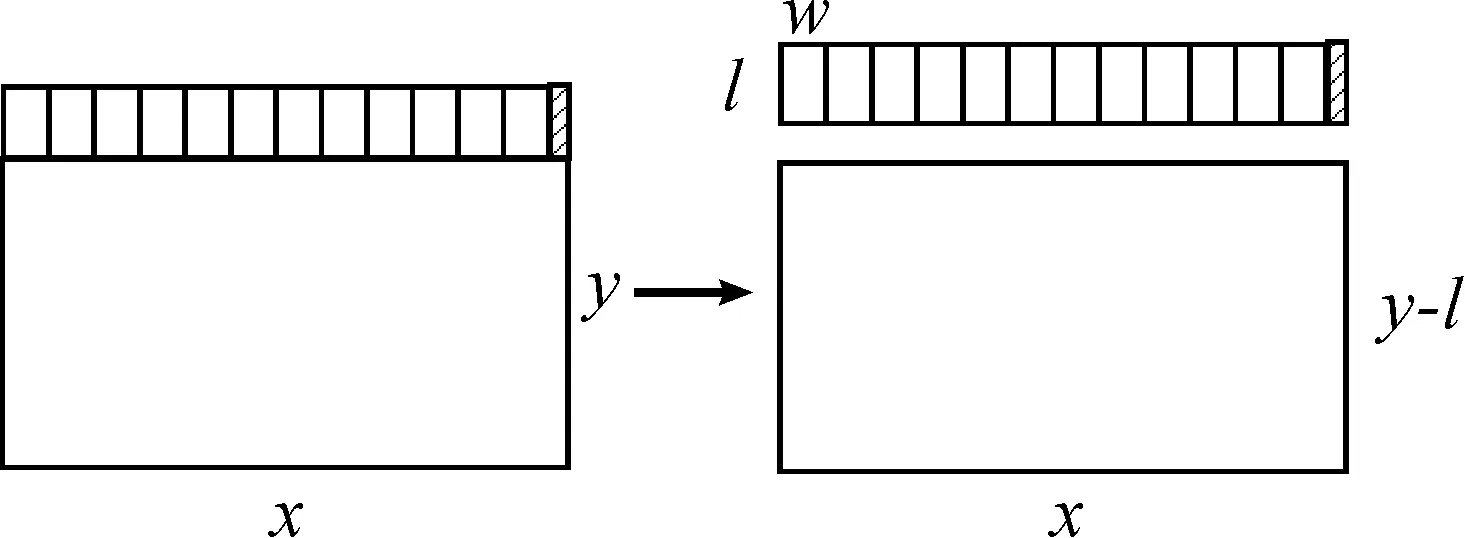
图1 条带横切
2) 竖切
如图2所示,从当前板材的左边剪切出1根Y向条带,条带的尺寸是y×l,令条带y×l可以冲裁出的毛坯数用Num(y) 表示,则有Num(y)=int(y/w)。剪切出1根Y向条带后剩余板材的尺寸是(x-l)×y,令其可以剪切出的毛坯数量为N(x-l,y),条带数为M(x-l,y)。令D(x,y)=1表示当前板材x×y第1刀的切割方向为竖切。按此切割方式,可得到如下关系式:
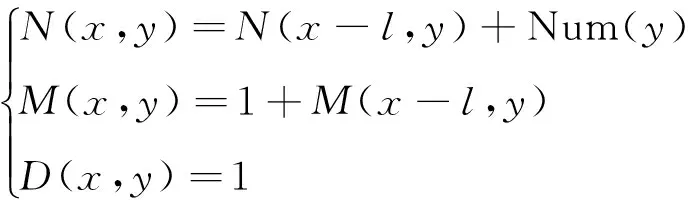
(2)
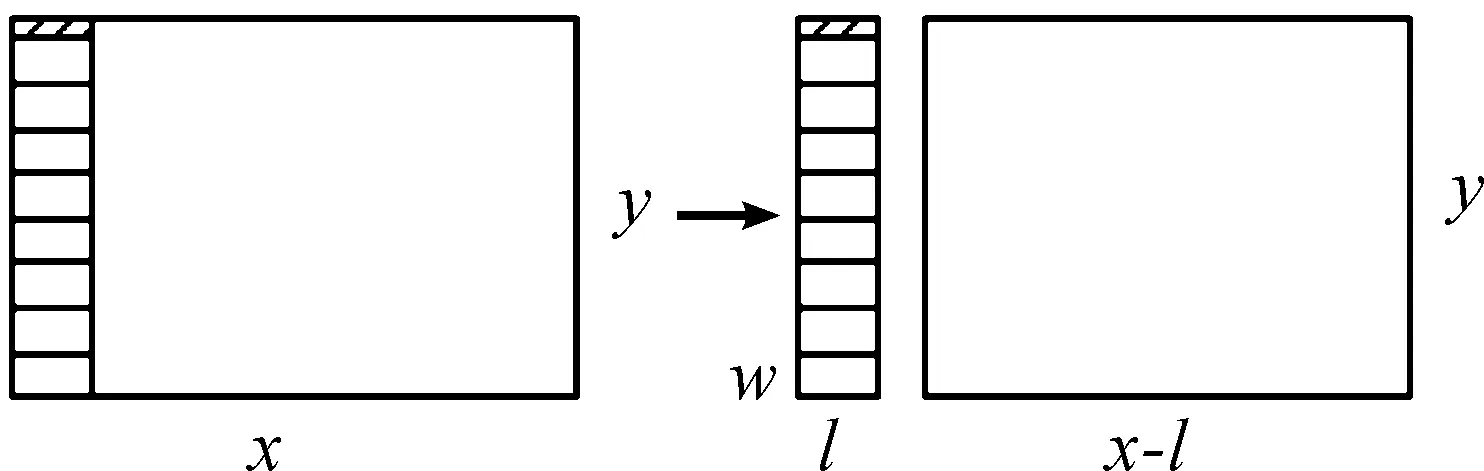
图2 竖切
2.2 毛坯数和条带数的优化
1) 毛坯数优化
根据规范多级排样方式和剪切冲裁下料工艺,从板材中剪切出条带时只能是横切和竖切两种方式。对于尺寸为x×y的当前板材,若第1刀的剪切方向选择横切,那么当前板材递归排样到底部时生成的条带数和毛坯数是由剩余板材x×(y-l)和当前产生的水平条带x×l来决定的。若第1刀的剪切方向选择竖切,那么当前板材递归排样到底部时生成的条带数和毛坯数是由剩余板材(x-l)×y和当前产生的垂直条带y×l来决定的。对于每一刀剪切方向的选择,是以当前板材最终可生成的毛坯数及其产生的条带数作为选择依据的。首先考虑板材的最大利用率,即毛坯数最优的切割方式,在板材利用率相同的情况下,选择切割工艺最优的切割方式。毛坯数的优化处理方式如下:
N0(x,y)={max(N0(x,y-l)+Num(x),
max(N0(x-l,y)+Num(y)}
(3)
2) 条带数优化
保证在毛坯数最优的前提下,为保证切割工艺最优,需要从减少条带数对单一尺寸矩形排样进行优化。
初始尺寸为L×W的板材,在不断地剪切出竖值条带或垂直条带后,当剩余板材最终不能冲裁出一个毛坯时,说明递归排样到了底部,生成一种新的排样方案(当前排样方式)。为实现在毛坯数最大化的前提下,得到条带数最少的优化排样方式,每当递归排样到了底部时(即N(x,y)=0),依照如下处理方式进行优化:
① 当N(L,W)>N0(L,W)时,令N0(L,W)=N(L,W),M0(L,W)=M(L,W),D0(L,W)=D(L,W)。
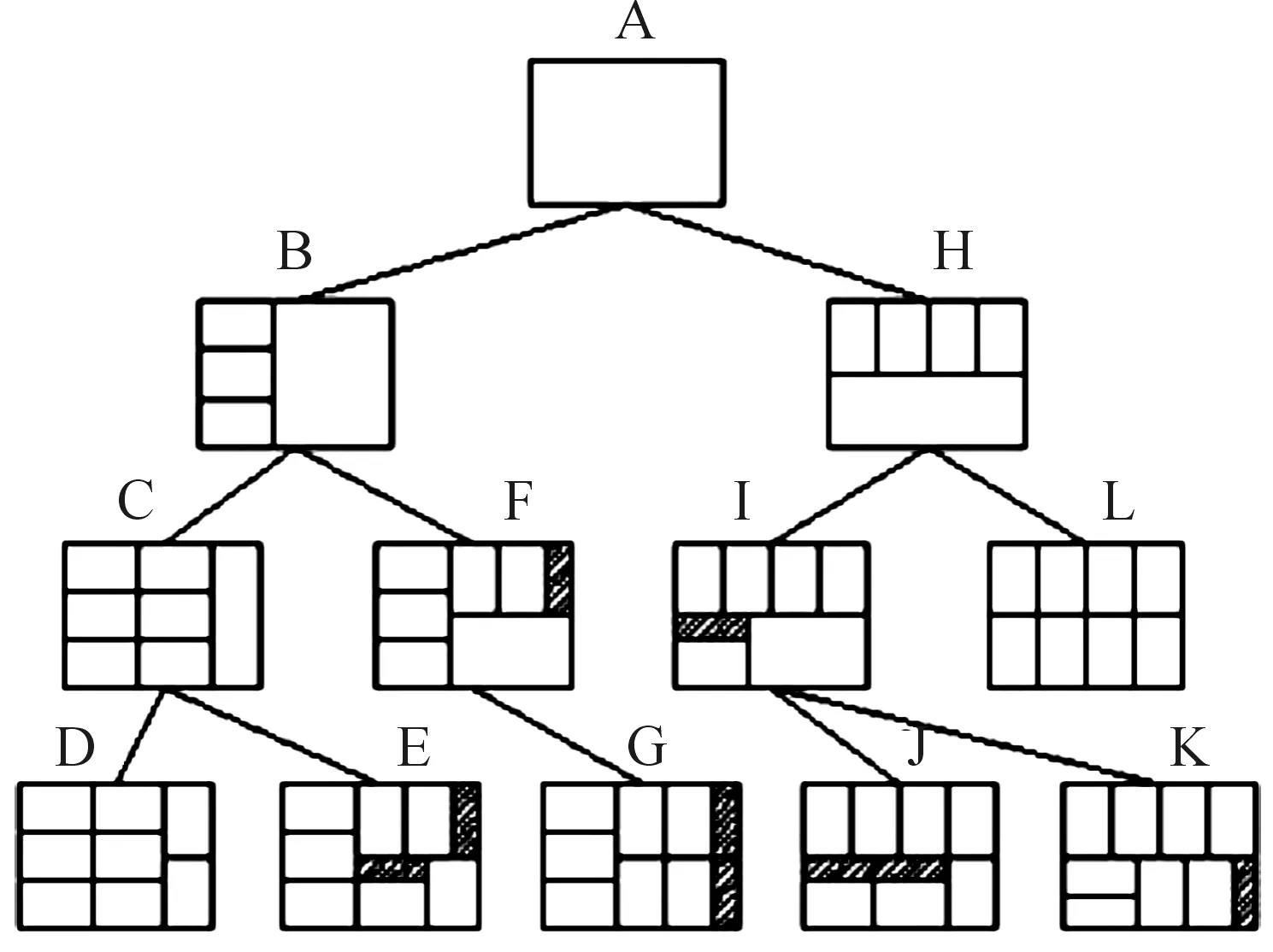
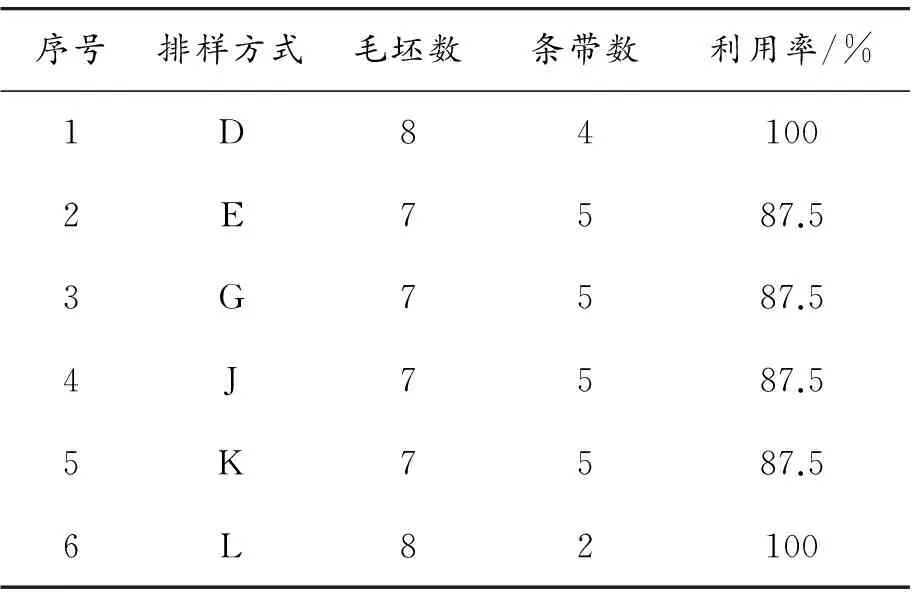
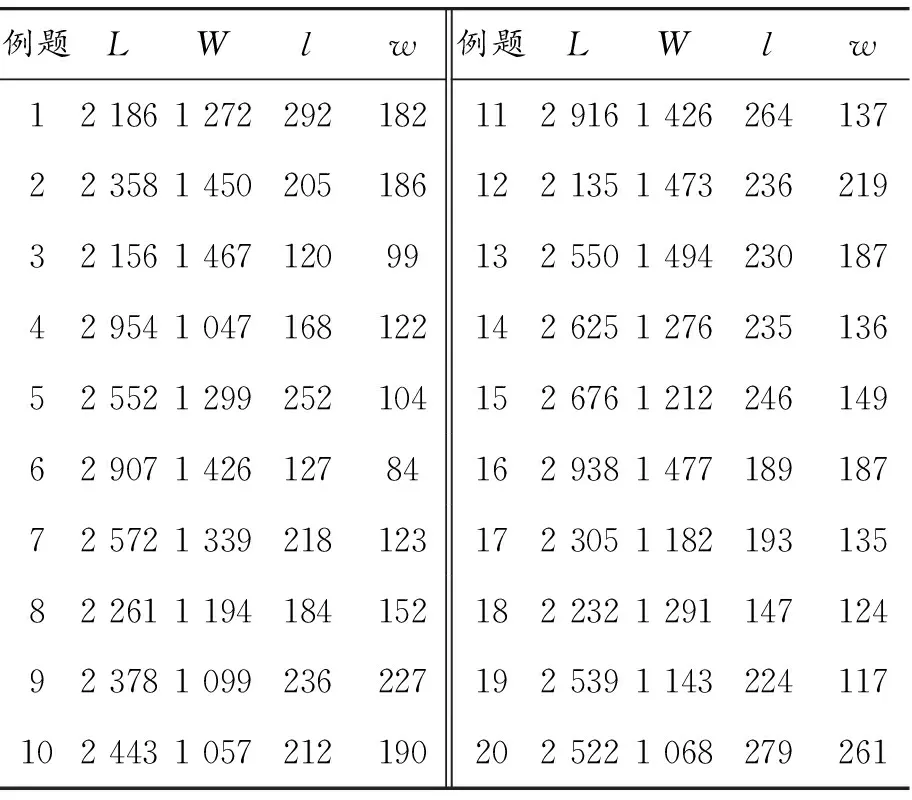
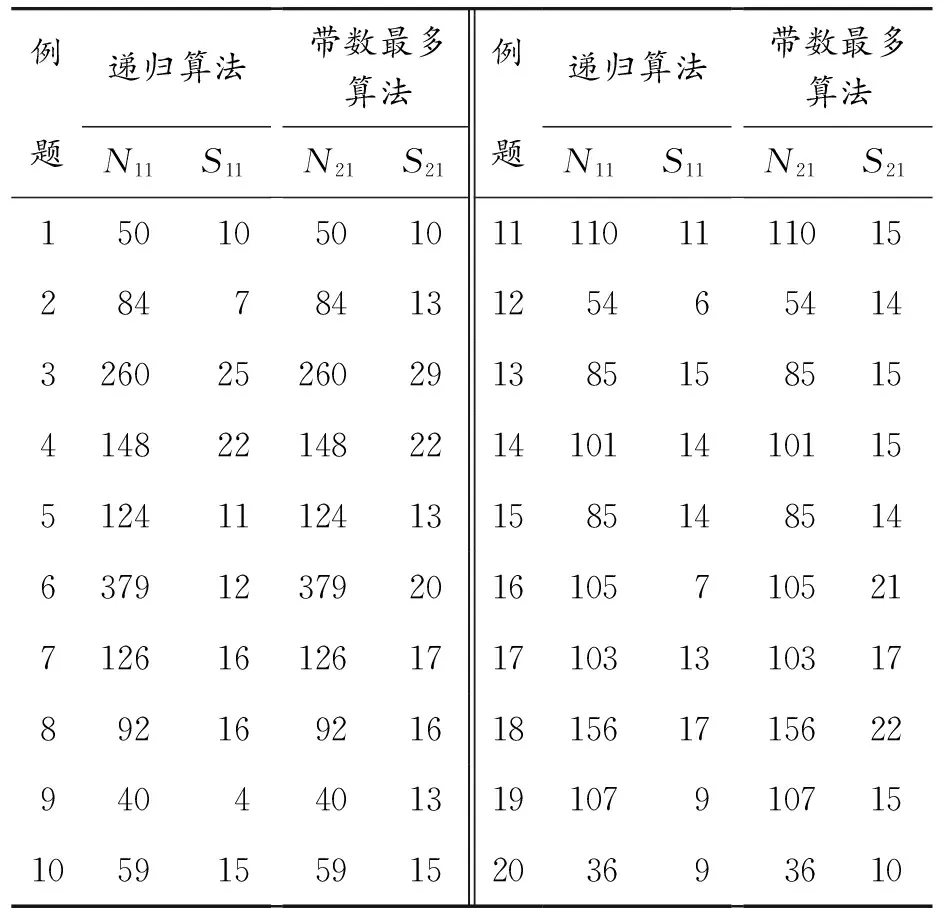
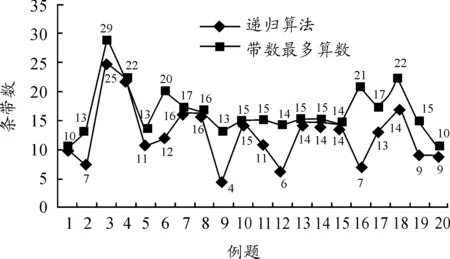
② 当N(L,W) ①和②表示当前最优排样方式与当前排样方式生成的毛坯数不相同时,则优选毛坯数多的排样方式作为当前最优排样方式,即以毛坯数最优为一级优化目标,实现材料利用率的最大化。 ③ 当N(L,W)=N0(L,W)且M0(L,W)>M(L,W)时,令N0(L,W)=N(L,W),M0(L,W)=M(L,W),D0(L,W)=D(L,W)。表示当前最优排样方式与当前排样方式生成的毛坯数相同时,则优选条带数少的排样方式作为当前最优排样方式,即保证在毛坯数最优的前提下以减少条带数为二级目标,简化切割工艺提高排样效率。 根据①~③得到如下表达式: (4) 根据上述可知,如果当前排样方式相对当前最优排样方式不能引起解的改善,将直接返回上一层递归调用;否则把当前排样方式置为当前最优排样方式,然后再返回到上一层递归调用,继续执行指定的递归操作,直到遍历所有的递归分支,搜索得到毛坯数和条带数最优的排样方式。 2.3 递归函数的构建 设递归函数RecFun(x,y,NP,MP,D)用于求解板材尺寸为L×W、毛坯尺寸为l×w的排样方式最优毛坯数,其中:参数NP表示剪切到当前板材尺寸为x×y时已经切出的毛坯数量;参数MP表示剪切到当前板材尺寸为x×y时已经切下的条带数量;参数D表示一维数组D用于记录条带切割的方向,“0”表示条带方向为竖直切割,“1”表示条带方向为水平切割。 当前最优排样方式的毛坯数(N0(L,W))和条带数(M0(L,W))的初始值为N0(L,W)=M0(L,W)=0。根据式(1)~(4),递归函数RecFun(x,y,NP,MP,D)为: Setp1If(min(x,y) If((NP>N0(L,W) or (NP=N0(L,W) andMP letN0(L,W)=NP; M0(L,W)=MP; D0=D; N0(x,y)=M0(x,y)=0; Return 0; Setp2If(y≥landx≥w) then letD(MP+1)=1; Nx=RecFun(x,y-l,NP+Num(x),MP+1,D)+Num(x); Mx=1+M(x,y-l); Setp3If(x≥landy≥w) then letD(MP+1)=0; Ny=RecFun(x-l,y,NP+Num(y),MP+1,D)+Num(y); My=1+M(x-l,y); Setp4If(Nx>Ny) then letN0(x,y)=Nx,M0(x,y)=Mx; If(Nx If(Nx=Ny) then letN0(x,y)=NxorN0(x,y)=Ny,M0(x,y)=min(Mx,My); Setp5ReturnN0(x,y)。 2.4 求解步骤 基于Win 32位系统平台,应用 C++面向对象编程语言开发了单一尺寸矩形毛坯排样系统,以测试验证本文所述算法的有效性。初始调用递归函数RecFun()时,实参板材尺寸为L×W、形式参数NP和MP对应的实参值均为0,即RecFun(L,W,0,0,D),具体求解过程如下: 步骤1 输入毛坯l×w和板材L×W的尺寸值。 步骤2 令N0(L,W)=M0(L,W)=0。 步骤3 调用递归函数RecFun(L,W,0,0,D)进行优化排样,求出N0(L,W)、M0(L,W)及D0。 步骤4 根据板材L×W、毛坯l×w和D0中前M0(L,W)个元素,画出排样图。 3.1 毛坯数实验计算分析 1) 应用例题 毛坯尺寸l×w为3×2、板材尺寸L×W为8×6,如图3所示,应用递归算法进行排样。 图3 毛坯和板材尺寸 2) 例题求解 初始条件:x=8,y=6;N0(L,W)=M0(L,W)=0。 递归结束条件: Min(x,y)<2 OR Max(x,y)<3。 通过调用递归函数RecFun(8,6,0,0,D)进行优化排样,整个递归调用排样过程,如图4所示。 图4 递归排样执行过程示意图 3) 排样分析 根据图4可知:本例题所有可能的排样方式为D、E、G、J、K、L共6种,对应毛坯数、板材利用率如表1所示。 表1 本例题所有可能的排样方式 根据图4和表1可知:如果只考虑板材的利用率,最优的排样方式为D、L,板材利用率均为100%,而E、G、J、K这4种排样方式的板材利用率仅为87.5%。在材料分割领域,利用排样方式为D、L进行下料可以最大化提高材料的利用价值,显然优于E、G、J、K这4种排样方式,可见在下料的过程中考虑毛坯数、利用计算机辅助排样提高材料利用率具有重要的价值和意义。排样方式L的条带数2优于条带数为4的排样方式D,利用本文算法同时考虑毛坯数和条带数,确定最优排样方式为L。 3.2 条带数实验计算分析 3.2.1 实验数据 如表2所示,板材和毛坯的尺寸范围基本涵盖了实际生产中的板材和毛坯的尺寸比例。在实际生产中,若板材和毛坯的尺寸含有小数,可通过等比例转换成整数。根据表2,使用程序随机生成20道例题,如表3所示。基于本文算法,在保证材料利用率最大化的前提下,生成条带数最少的排样方式(即递归算法)和条带数最多的排样方式(在递归算法的基础上进行改进,在保证毛坯数最优的情况下,生成条带数最多的排样方式,即带数最多算法),以便进行对比分析。 表2 板材和毛坯的尺寸范围 mm 表3 随机生成的20道例题 3.2.2 实验结果及其分析 1) 实验结果 表4的实验结果是通过单一矩形毛坯排样系统计算获得。实验数据符号的含义:N11、S11分别表示运用本文递归算法求解得到的毛坯数、条带数;N21、S21分别表示基于本文所述算法的带数最多算法排样求解得到的毛坯数、条带数。 表4 排样实验结果 2) 实验结果分析 根据表3和表4可知:条带数相同的例题为1、4、8、10、13、15,而例题2、3、5、6、7、9、11、12、14、16、17、18、19、20条带数互不相同,具体如图5所示。 图5 基于递归算法和带数最多算法排样条带数比较 如果N11=N21、S11=S21,说明在实现毛坯数最优的前提下其排样方式的条带数也是最优的(切割工艺最优);如果N11=N21、S11≠S21,说明能实现毛坯数最优的排样方式,其条带数未必是最优的,即存在条带数不一样的排样方式。根据表4和图5可知:对于任何一道例题均有N11=N21、S11≤S21,说明应用本文的递归算法可以在保证毛坯数最优的前提下实现条带数最少,即使切割工艺最优。表5为递归算法和带数最多算法的条带数平均值。 表5 条带数平均值 根据表4中递归算法和带数最多算法排样结果,各道例题条带数的差值范围为0~14。根据表5实验数据,这两种算法的条带数平均值的差值为3.65。基于剪冲工艺,单一尺寸矩形毛坯下料工作量主要取决于从板材中剪出所有条带的时间开销。由于切割工艺的复杂性与板材剪切出的条带数近似成正比,若条带数越多那么相应地下料工作量也就越大,排样效率就越低。根据表4条带数差值范围和表5条带数平均值差值,表明在单一矩形毛坯无约束排样中对条带数进行优化是必要的,在材料利用率最大化的前提下尽可能地减少条带数以简化切割工艺具有重要的现实意义。 从实验结果可知:本文递归算法能在保证毛坯数最优的前提下实现切割工艺最优。 采用本文提出的递归算法对单一尺寸矩形毛坯排样问题进行求解,能同时实现毛坯数最优和切割工艺最优。相对于其他算法,一方面本文算法实现较简单,在开发排样系统的过程中软件工程师将算法转化为对应代码很容易,这点在工程应用中比较重要;另一方面该算法属于枚举搜索法,能得到条带数最小的解,保证解的最优性。在涉及二维下料的制造行业中,通常会涉及到二维矩形板材的选购,若有多种尺寸不同、厚度和材质相同的板材提供选择,企业可以利用本文算法进行计算分析,优选利用率最大化的板材尺寸。企业在下料环节,则应用该算法在板材利用率最大的所有排样方案中选择切割工艺最优的排样方式,以有效降低原材料成本和减少人工成本。 [1] 李秋蓉.考虑切割刀数的板材下料算法研究[D].南宁:广西大学,2013. [2] 王晓庆.基于层排样方式的矩形毛坯下料算法[D].南宁:广西师范大学,2011. [3] 田双.基于Sigma Nest的板材下料问题研究[J].现代机械,2014 (4):25-27,31. [4] ARSLANOV M Z.Continued fractions in optimal cutting of a rectangular sheet into equal small rectangles[J].European Journal of Operational Research,2000,125:239-248. [5] 潘卫平,陈秋莲,崔耀东.考虑切割刀数的最优两段排样算法研究[J].广西大学学报,2014,39(3):687-692. [6] CUI Y,GU T,HU W.Recursive algorithms for the optimum cutting of equal rectangles[J].International Journal of Computers and Applications,2011,33(2):103-107. [7] 王桂兰,成亚云,朱龙彪,朱志松.满足“一刀切”要求的木工板排样优化研究[J]工程设计学报,2014,21(3):212-216. [8] 秦旭辉.圆形件剪切下料的排样研究[D].长春:吉林大学,2014. [9] 陈奇.数控切割下料与排程优化技术及应用研究[M].武汉:华中科技大学,2012. [10] 郑文.基于多线程求解一维下料问题的递归算法[D].南宁:广西大学,2011. (责任编辑陈 艳) RecursiveAlgorithmAppliedStudyonaSingleRectangleBlanksUnconstrainedOptimalLayout LI Haisheng (College of Physics and Electronic Engineering, Guangxi Normal University for Nationalities, Chongzuo 532200, China) 2017-05-04 国家自然科学基金资助项目(61363026);广西民族师范学院校级科研项目(2016YB037) 李海生(1980—),男,广西扶绥人,硕士,讲师,主要从事网络技术和排样计算方面的研究,E-mail:lihsmsy@126.com。 李海生.递归算法在单一矩形毛坯无约束最优排样中的应用[J].重庆理工大学学报(自然科学),2017(9):125-131. formatLI Haisheng.Recursive Algorithm Applied Study on a Single Rectangle Blanks Unconstrained Optimal Layout[J].Journal of Chongqing University of Technology(Natural Science),2017(9):125-131. 10.3969/j.issn.1674-8425(z).2017.09.020 TP399 A 1674-8425(2017)09-0125-073 实验计算分析
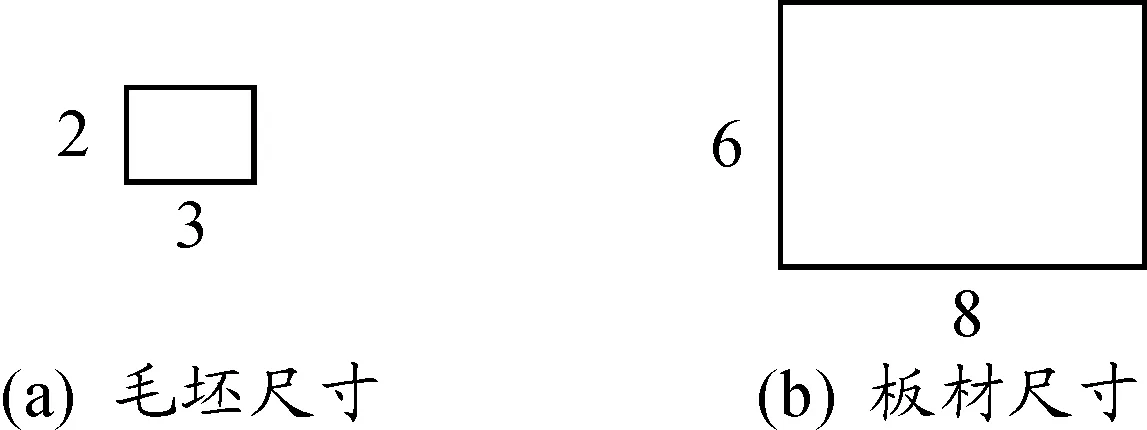


4 结束语

