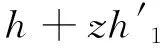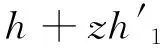Bloch型双调和映照
李西振, 陈行堤
(华侨大学 数学科学学院, 福建 泉州 362021)

Bloch型双调和映照
李西振, 陈行堤
(华侨大学 数学科学学院, 福建 泉州 362021)
研究 Bloch 型双调和函数的判别准则和系数估计.通过建立双调和函数的线性和复合性质,得到双调和函数的 Bloch 型判别法则.利用双调和的表示理论及调和函数的 Pre-Schwarz 导数估计,给出 Bloch 型双调和函数的单叶性判定定理及系数估计.
Bloch函数; 双调和映照; 系数估计; 拟正则映照
Abstract: This paper studies the criterion and coefficient estimate of Bloch-type biharmonic mappings. After establishing the linear and composite properties of biharmonic mappings, we give a criterion for biharmonic mappings to be Bloch-type. Combining the representation theorem of the biharmonic mappings with the estimation of Pre-Schwarz derivative of harmonic mappings, we obtain a univalent criterion and some coefficient estimates of biharmonic mappings for Bloch-type biharmonic mappings.
Keywords: Bloch function; biharmonic mapping; coefficient estimate; quasiregular mapping
1 预备知识
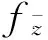

设f为单位圆盘D到自身上的保向映照,若它满足f∈ACL2(D),且不等式|f(z)|2≤KJf(z)在D上几乎处处成立,则称f为D上的K-拟正则映照,其中,|f|=|fz|+||.
如果一个C2函数f满足

则称为Bloch型函数,记这类函数全体为B.如果f为D上的解析函数时,记这类函数全体为BA.如果f为D上的调和函数时,记这类函数全体为BH.如果f为D上的双调和函数时,记这类函数全体为BBH,则BA⊆BH⊆BBH⊆B.文献[7-13]对类Bloch型函数BA,BH开展了研究,其中,文献[10]证明了定理A,B.




本文主要研究具有表达式f=|z|2h的双调和映照类.同时,给出该类双调和Bloch型函数的系数估计.
2 主要结论及证明
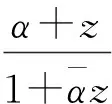
2)f∘φα∈BBH.
证明 1) 由假设知,存在两个解析函数h1,h2满足

从而有



同理可得
因此,有
故由f∈BBH可知,F∈BBH.
2) 令F=f∘φα=|φα(z)|2h∘φα,则有
同理可得
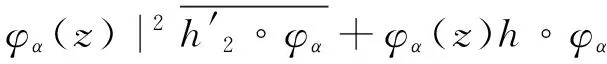
从而有
因此,有β(f)=β(F),这隐含着f∘φα∈BBH,证毕.

证明 令α∈D,定义

则Φ(z)在D上单叶调和,且满足Φ(0)=0,Φz(0)=1.因此,它的展开式的系数a2(α)的模有界,且满足

这隐含着


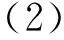
由于


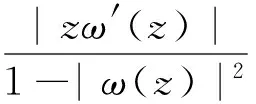
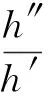
假设函数ω∶D→D解析,定义
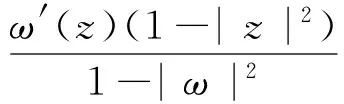
定理2假设f=|z|2h∈BBH,h=h1+h2,且f是K-拟正则的.对0<ε<1,令


证明 由假设f∈BBH,可得

又由于f为K-拟正则映照,有

上式隐含着

由于

所以可得

由定理C知函数F在D上单叶.证毕.

定理3若f=|z|2h∈BBH是K-拟正则的,且|h| 上式中:M为一正常数. 令z=reit,t∈(0,2π),r∈(0,1),则有 所以 又由于β(f)的定义可知,对∀z∈D,有 结合式(3),可得∀z∈D.由 进而有 从而有 将z=reit,t∈(0,2π),r∈(0,1)代入,可得 由式(4),(5)可得 [1] LEWY H.On the non-vanishing of the Jacobian in certain one-to-one mappings[J].Bulletin of the American Mathematical Society,1936,42(10):689-698. [2] DUREN P.Harmonic univalent functions[M].Cambridge:Cambridge University Press,2004:1-17. [3] CLUNIE J,SHEIL-SMALL T.Harmonic univalent functions[J].Ann Acad Sci Fenn Ser A,1984,9(1):3-25. [4] ABDULHADI Z,MUHANNA Y,KHURI S.On univalent solutions of the biharmonic equation[J].J Inequal Appl,2005,5(2005):469-478. [5] KALAJ D.On quasiregular mappings between smooth Jordan domains[J].Journal of Mathematical Analysis and Applications,2010,362 (1):58-63. [6] AHLFORS L V,EARLE C J.Lectures on quasiconformal mappings[M].New York:American Mathematical Society,1966:21-34. [7] ANDERSON J M,CLUNIE J,POMMERENKE C.On Bloch functions and normal functions[J].J Reine Angew Math,1974,270:12-37. [8] DANIKAS N.Some Banach spaces of analytic functions, function spaces and complex analysis, joensuu[J].Univ Joensuu Dep Math Rep Ser,1997,2:9-35. [9] POMMERENKE C.On Bloch functions[J].J London Math Soc,1970,2(2):689-695. [10] EFRAIMIDIS I,GAONA J,HERNNDEZ R,etal.On harmonic Bloch-type mappings arXiv preprint arXiv[DB/OL].[2016-07-15][2016-09-05].https:∥arxiv.org/pdf/1607.04626v1.pdf. [11] POMMERENKE C.Boundary behaviour of conformal maps[M].Berlin:Springer-Verlag,1992:185-187. [12] SEIDEL J,WALSH L.On the derivatives of functions analytic in the unit circle and their radii of univalence and ofp-valence[J].Trans Amer Math Soc,1942,52(1):128-216. [13] ZHU K. Operator theory in function spaces, marcel dekker[M]. New York: American Mathematical Soc,2007:101-132. [15] BEARDON A,MINDA D.The hyperbolic metric and geometric function theory[J].Quasiconformal Mappings and Their Applications,2007,3:9-56. (责任编辑: 陈志贤英文审校: 黄心中) OnBiharmonicBloch-TypeMappings LI Xizhen, CHEN Xingdi (School of Mathematical Sciences, Huaqiao University, Quanzhou 362021, China) 10.11830/ISSN.1000-5013.201609021 2016-09-15 陈行堤(1976-),男,教授,博士,主要从事函数论的研究.E-mail:chxtt@hqu.edu.cn. 国家自然科学基金资助项目(11471128); 福建省自然科学基金计划资助项目(2014J01013); 华侨大学青年教师科研提升资助计划(ZQN-YX110); 华侨大学研究生科研创新能力培育计划资助项目(1511313003) O 174.55 A 1000-5013(2017)05-0737-05