求解时变线性不等式离散算法的设计与分析

郭东生， 徐凤

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

求解时变线性不等式离散算法的设计与分析

郭东生， 徐凤

(华侨大学 信息科学与工程学院， 福建 厦门 361021)

提出一种用于求解时变线性不等式的数值算法.通过引入一个时变向量(其每个元素都大于或等于零)，将时变线性不等式转化为一个时变矩阵向量方程，并给出用于求解该方程的连续时间模型(即神经网络).采用欧拉差分公式将其离散化，推导得到相应的离散算法，并通过理论分析和数值实验验证该离散算法的有效性.结果表明：所提出的离散算法的稳态误差(SSRE)具有O(τ2)的变化规律，当τ的数值减小10倍，算法的稳态误差可减小100倍.

线性不等式； 时变； 离散算法； 欧拉差分公式； 稳态误差

Abstract： A numerical algorithm for time-varying linear inequality solving is proposed. By introducing a time-varying vector (of which each element is greater than or equal to zero), we convert the time-varying linear inequality to a time-varying matrix-vector equation. A continuous-time model (i.e., the neural network) is then presented to solve such an equation. Using Euler′s difference formula to discretize the continuous-time model, we propose the corresponding discrete algorithm. Both theoretical analysis and numerical results further substantiate the efficacy of such algorithm. These results also indicate that the steady-state residual error (SSRE) of the proposed discrete algorithm changes in anO(τ2) manner with beingτthe sampling gap; when theτvalue decreases by 10 times, the SSRE reduces by 100 times.

Keywords： linear inequality； time-varying； discrete algorithm； Euler′s difference formula； steady-state residual error

近年来，不等式在科学研究和工程应用领域扮演着越来越重要的角色[1-6].在不等式的研究中，如何有效求解形如Ax≤b的线性不等式是一个重要课题，且已受到广泛关注.对于线性不等式，许多研究学者提出了相应的求解方法[7-10]，如文献[7]设计的迭代算法，开发的连续时间神经网络模型，文献[8]展示的离散时间神经网络模型.但是，这些方法都是针对时不变线性不等式进行设计的，而对于时变线性不等式，采用前述方法进行求解得到的结果会有明显滞后误差[11].针对时变线性不等式的求解，文献[11]设计一种新型神经网络模型，并通过对比来说明该模型的有效性和优越性.文献[12-13]分别开发以隐式动力学方程和显式动力学方程描述的两种神经网络模型.为了硬件(如数字电路)实现的目的，针对文献[13]的神经网络模型，本文设计开发相应的数值算法,用以求解时变线性不等式.

1 问题和模型描述

不失一般性，所研究的时变线性不等式[11-13]为

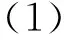
式(1)中:A(t)∈Rn×n和b(t)∈Rn分别是光滑时变的系数矩阵和向量;x(t)∈Rn是需要求解(1)得到的未知向量.需要说明的是，式(1)是一个具有代表性的时变线性不等式，文中的设计方法可拓展求解其他类型的不等式(如时变李雅普诺夫矩阵不等式[14]).为了保证式(1)中x(t)的存在，文中仅考虑系数矩阵A(t)在时间t∈[0，+∞)内是非奇异的情况.

文献[13]展示了时变线性不等式(1)的求解可等价于时变矩阵向量方程的求解，即

式(2)中:Λ(t)=[λ1(t)，λ2(t)，…，λn(t)]T∈Rn是一个需要求解的未知向量;时变向量Λ2(t)=D(t)×Λ(t)∈Rn，其中,对角线矩阵D(t)∈Rn×n，D(t)=diag(λ1(t)，λ2(t)，…，λn(t)).

基于上述转换，文献[13]设计了如下的神经网络模型，用以求解时变矩阵向量方程(2)及时变线性不等式(1)，即

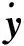
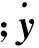
定理1对于时变线性不等式(1)，给定一个光滑时变的非奇异系数矩阵A(t)∈Rn×n和一个光滑时变的系数向量b(t)∈Rn,则模型(3)的状态向量y(t)从一个随机产生的初始状态y(0)∈R2n出发，收敛到时变矩阵向量方程(2)的一个精确解.该解的前n个元素组成时变线性不等式(1)一个精确的时变解.

2 新离散算法及其理论分析

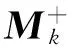
式(4)中：h=τγ>0∈R为步长.式(4)便是文中所提出用以求解(1)的离散算法.

定理2所提出的离散算法是一个一致的和收敛的方法，且对于所有的时间tk∈[t0，tfinal]，以其截断误差O(τ2)的阶数收敛.

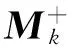
显然，去掉式(5)中的O(τ2)，正是文中所提出的离散算法(4).换言之，离散算法(4)的截断误差为O(τ2)，这表明该算法具有2阶的一致性.

综合上述分析可得，离散算法(4)是零稳定和一致的[19].因此，所提出的离散算法(4)是一个一致的和收敛的方法，且对于所有的时间tk∈[t0，tfinal]，以其截断误差O(τ2)的阶数收敛.证毕.

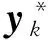
3 数值实验验证

对于时变线性不等式(1)，系数矩阵A(t)和向量b(t)为

当τ=0.01和h=0.5时，采用所提离散算法求解变线性不等式(1)，其数值结果如图1所示.

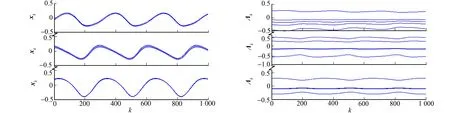
(a) xk的轨迹 (b) Λk的轨迹

(c) 计算误差的轨迹 (d) 测试误差的轨迹图1 采用离散算法求解时变线性不等式(1)的数值实验结果(τ=0.01， h=0.5)Fig.1 Numerical results of using discrete algorithm (τ=0.01， h=0.5) to solve time-varying linear inequality (1)

由图1(a),(b)可知：基于5个随机产生的初始状态，由离散算法计算得到的xk和Λk的状态轨迹是时刻变化的.图1(c)显示了计算误差‖ek‖2=‖Qkyk-bk‖2的变化特点，即计算误差快速减小并维持在一个小的数值范围内，且其最大稳态误差为1.056×10-3.这就意味着xk和Λk正是时变矩阵向量方程(2)的时变解.对于满足式(2)的xk，这就是时变线性不等式(1)的一个时变解，即Akxk≤bk.

当τ=0.001和h=0.5时，采用所提离散算法求解变线性不等式(1)，其数值结果如图2所示.

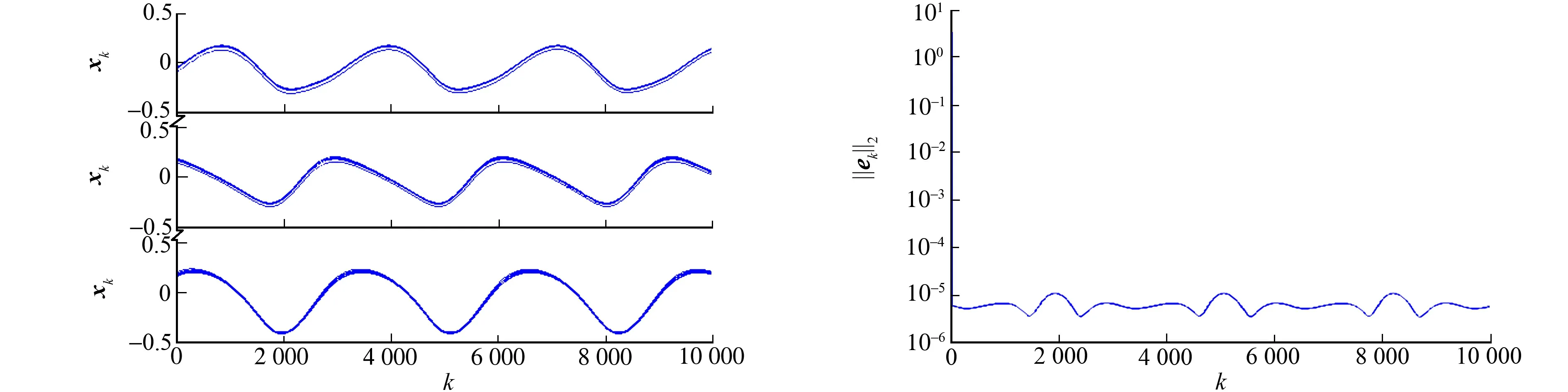
(a) xk的轨迹 (b) 计算误差的轨迹图2 采用离散算法求解时变线性不等式(1)的数值结果(τ=0.001， h=0.5)Fig.2 Numerical results of using discrete algorithm (τ=0.001， h=0.5) to solve time-varying linear inequality (1)

由图2(a)可知：由离散算法计算得到xk的状态轨迹是时变的.由图2(b)可知：计算误差快速减小并维持在一个小数值范围内，且其最大稳态误差为1.059×10-5.显然，这些结果再次表明离散算法能有效求解时变线性不等式(1).另外，对比图1(c)和图2(b)可知：随着τ的减小(从0.01到0.001)，相应的稳态误差也减小(从10-3到10-5).因此，离散算法的计算性能可以通过减小τ的数值来得到提高.

为了进一步研究，采用不同的τ和h来对所提出的离散算法进行数值实验，结果如图3,4所示.

(a) τ=0.1 (b) τ=0.01 (c) τ=0.001图3 不同τ值采用离散算法求解时变线性不等式(1)的误差状态轨迹(h=0.4)Fig.3 Error state trajectory of using discrete algorithm under different τ values (h=0.4) to solve time-varying linear inequality (1)

(a) τ=0.1 (b) τ=0.01 (c) τ=0.001图4 不同的τ值下采用离散算法求解时变线性不等式(1)的误差状态轨迹(h=0.6)Fig.4 Error state trajectory of using discrete algorithm under different τ values (h=0.6) to solve time-varying linear inequality (1)

由图3,4可知：对于固定τ的数值，采用不同的h的数值，离散算法的计算性能都有所不同(即相应的稳态误差都不一样).特别地，对于固定的h，减小τ的数值，离散算法的计算性能能够得到更有效的提高.具体而言，当τ的数值减小10倍，离散算法的稳态误差能够减小100倍，即所提出的离散算法的稳态误差具有O(τ2)的变化规律.这也就意味着可通过合理地减小τ的值来有效地满足应用实践中所需要的精度.总的来说，上述的数值实验结果很好地表明了所提出离散算法的有效性.

4 结束语

为求解时变线性不等式(1)，结合欧拉差分公式推导得到一种离散算法，并给出相应的理论结果来说明其计算性能.通过数值实验，进一步验证所提出的离散算法的有效性.结果表明，所提出的离散算法的稳态误差与采样间隔τ具有O(τ2)的变化关系，可以有效地求解时变线性不等式(1).

[1] 庄梁，林灿煌，孙洪飞.受扰线性不确定系统鲁棒H∞混合镇定[J].华侨大学学报(自然科学版),2017,38(2):147-152.DOI:10.11830/ISSN.1000-5013.201702003.

[2] 朱剑峰.调和K-拟共形映照下Heinz不等式的精确估计[J].华侨大学学报(自然科学版),2014,35(3):354-357.DOI:10.11830/ISSN.1000-5013.2014.03.0354.

[3] KLAPPER A.Improved multi-covering bounds from linear inequalities and supercodes[J].IEEE Transactions on Information Theory，2004，50(3):532-536.DOI:10.1109/TIT.2004.825504.

[4] GUO Dongsheng，ZHANG Yunong.Acceleration-level inequality-based MAN scheme for obstacle avoidance of redundant robot manipulators[J].IEEE Transactions on Industrial Electronics，2014，61(12):6903-6914.DOI:10.1109/TIE.2014.2331036.

[5] GUO Dongsheng，LI Kene.Acceleration-level obstacle-avoidance scheme for motion planning of redundant robot manipulators[J].Proceedings of IEEE International Conference on Robotics and Biomimetics.Qingdao:IEEE Press，2016:1313-1318.DOI:10.1109/ROBIO.2016.7866508.

[6] XIAO Lin，ZHANG Yunong.Dynamic design， numerical solution and effective verification of acceleration-level obstacle avoidance scheme for robot manipulators[J].International Journal of Systems Science，2016，47(4):932-945.DOI:10.1080/00207721.2014.909971.

[7] YANG Kai，MURTY K G，MANGASARIAN O L.New iterative methods for linear inequalities[J].Journal of Optimization Theory and Applications，1992，72(1):163-185.DOI:10.1007/BF00939954.

[8] CICHOCKI A，BARGIELA A.Neural networks for solving linear inequality systems[J].Parallel Computing，1997，22(11):1455-1475.DOI:10.1016/S0167-8191(96)00065-8.

[9] LABONTE G.On solving systems of linear inequalities with artificial neural network[J].IEEE Transactions on Neural Networks，1997，8(3):590-600.DOI:10.1109/72.572098.

[10] XIA Youshen，WANG Jun，HUNG D L.Recurrent neural networks for solving linear inequalities and equations[J].IEEE Transactions on Circuits and Systems Ⅰ，1999，46(4):452-462.DOI:10.1109/81.754846.

[11] XIAO Lin，ZHANG Yunong.Zhang neural network versus gradient neural network for solving time-varying linear inequalities[J].IEEE Transactions on Neural Networks，2011，22(10):1676-1684.DOI:10.1109/TNN.2011.2163318.

[12] GUO Dongsheng，ZHANG Yunong.A new variant of the Zhang neural network for solving online time-varying linear inequalities[J].Proceedings of the Royal Society A，2012，468(2144):2255-2271.DOI:10.1098/rspa.2011.0668.

[13] GUO Dongsheng，ZHANG Yunong.ZNN for solving online time-varying linear matrix-vector inequality via equality conversion[J].Applied Mathematics and Computation，2015，259(C):327-338.DOI:10.1016/j.amc.2015.02.060.

[14] GUO Dongsheng，ZHANG Yunong.Zhang neural network for online solution of time-varying linear matrix inequality aided with an equality conversion[J].IEEE Transactions on Neural Networks and Learning Systems，2014，25(2):370-382.DOI:10.1109/TNNLS.2013.2275011.

[15] MATHEWS J H，FINK F D.Numerical methods using MATLAB[M].4th ed.New Jersey:Prentice Hall，2004:1-696.

[16] 张雨浓，郭东生，徐思洪,等.未知目标函数之一阶数值微分公式验证与实践[J].甘肃科学学报，2009，21(1):13-18.DOI:10.3969/j.issn.1004-0366.2009.01.005.

[17] 张雨浓，侯占伟，郭东生.基于前向差分的一阶数值微分公式验证与实践[J].数学的实践与认识，2012，42(3):199-204.DOI:10.3969/j.issn.1000-0984.2012.03.031.

[18] MITRA S K.Digital signal processing: A computer-based approach[M].3rd ed.Beijing:Tsinghua University Press，2006.

[19] GRIFFITHS D F，HIGHAM D J.Numerical methods for ordinary differential equations: Initial value problems[M].London:Springer-Verlag London Ltd，2010.

(责任编辑： 陈志贤英文审校： 黄心中)

DesignandAnalysisofDiscreteAlgorithmforTime-VaryingLinearInequalitySolving

GUO Dongsheng， XU Feng

(College of Information Science and Engineering， Huaqiao University， Xiamen 361021， China)

10.11830/ISSN.1000-5013.201612043

2016-12-21

郭东生(1987-)，男，副教授，博士，主要从事神经网络、数值算法和机器人方面的研究.E-mail:gdongsh@hqu.edu.cn.

国家自然科学基金资助项目(61603143)； 福建省自然科学基金资助项目(2016J01307)； 华侨大学中青年教师科技创新计划资助项目(ZQN-YX402)； 华侨大学高层次人才科研启动项目(15BS410)

O 221.2; TP 183

A

1000-5013(2017)05-0732-05