事务约简和2项集支持度矩阵快速剪枝的Apriori改进算法

张健, 刘韶涛

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

事务约简和2项集支持度矩阵快速剪枝的Apriori改进算法

张健, 刘韶涛

(华侨大学 计算机科学与技术学院， 福建 厦门 361021)

在Apriori算法的改进算法M-Apriori基础上，为了进一步减少不必要的数据库扫描，引入事务约简技术，提出一种改进的MR-Apriori算法.考虑到M-Apriori算法会产生大量候选项集，为了实现对候选项集快速剪枝，加入一个自定义的2项集支持度矩阵，提出第2种改进的MP-Apriori算法.将事务约简和2项集矩阵快速剪枝一起引入到 M-Apriori算法中，提出第3种改进的MRP-Apriori算法.最后，在mushroom数据集上进行实验.结果表明：加入事务约简的MR-Apriori算法和加入2项集矩阵快速剪枝的MP-Apriori算法，运行时间相比原M-Apriori算法都有较大缩减，而同时结合两种优化策略的MRP-Apriori算法运行时间最短，验证了这两种优化策略的有效性.

关联规则； Apriori算法； 频繁项集； 支持度矩阵

Abstract： Based on the M-Apriori algprithm, an improved version of the Apriori algorithm, a transaction reduction technique is introduced and an improved algorithm, MR-Apriori, is proposed in the paper in order to further reduce unnessary database scans; Meanwhile, considering that the M-Apriori algorithm generates large amount of candidate itemsets during the running process, so as to quickly prune the candidate itemsets, a self-defined two-item set support matrix is added and a second improved algorithm, MP-Aproiri, is proposed in the paper. Then transaction reduction, accompanied by two-item set support matrix which is used to quickly prune the candidate itemsets, are combined together and a third improved algorithm, MRP-Aproiri, is proposed in the paper. Finally, an experiment is conducted on the mushroom dataset, the result shows that the MR-Apriori algorithm which uses the transaction reduction and the MP-Apriori algorithm which uses the two-item set support matrix that can quickly prune the candidate itemsets, is much faster than the M-Apriori algorithm, and the MRP-Apriori algotirhm which combines these two optimization strategies together gets the shortest time, therefore, it proves that these two optimization strategies are efficient.

Keywords： association rule； Apriori algorithm； frequent itemset； support matrix

关联规则挖掘是数据挖掘任务中一个重要的研究方面，旨在挖掘出数据库中潜在的关联关系[1-8].Apriori算法[1]是关联规则挖掘中最经典的算法，该算法基于“产生测试”框架，采用逐层迭代的方法得到频繁项集.Apriori算法思想简单，但也存在算法效率低的缺点.针对算法需要频繁扫描数据库的缺点，Al-Maolegi等[9]提出M-Apriori算法.M-Apriori算法采用了一种新的改进思路，大大减少了扫描数据库次数.但是，这种改进虽然减少了数据库扫描次数，但却存在很多不必要的扫描.Singh等[10]则是通过事务约简改进Apriori算法.纪怀猛[11]提出频繁2项集支持矩阵对候选项集快速剪枝的方法，对M-Apriori算法进行优化，优化后的算法命名为MP-Apriori算法.本文结合这两个优化算法，提出MRP-Apriori算法.

1 Apriori算法及M-Apriori算法

1.1Apriori算法及其改进

Apriori算法[1]采用宽度优先搜索的策略，算法有以下2个步骤.

步骤1扫描数据库，计算得到1项集的支持度，删去不满足最小支持度的项集，得到频繁1项集的集合.

步骤2由频繁1项集得到频繁2项集，频繁2项集得到频繁3项集，如此循环，直到不能找到频繁项集为止.

步骤2分为连接和剪枝.连接是频繁k-1项集Lk-1与自身进行连接，条件是两者前k-2个项都相同(称为可连接的)，最后一个元素不同，连接得到的结果是两者前k-2个项加上按字典顺序排列的两者的最后一个元素，即得到候选k项集Ck.剪枝运用Apriori性质[1]，即频繁项集的所有非空子集也都是频繁的，对候选k项集Ck进行剪枝，剪枝后得到频繁k项集Lk.

Apriori算法简单，但是它仍比较低效.原因主要有以下3个方面.

1) 需要多次扫描数据库.

2) 产生大量中间候选项集.

3) 候选项集求支持度时,需要和各条事务进行模式匹配，比较费时.

针对Apriori算法的这3点不足，国内外学者从各个方面来改进它的效率.DHP算法[2]引入Hash技术来减少候选2项集的生成；Partition算法[3]采用划分的办法，把数据库划分为若干个子库，在子库上求出局部频繁项集，最后再汇总求出全局频繁项集；Samping算法[4]随机选择一部分数据库样本，用这部分数据上的频繁项集代表全局频繁项集；DIC算法[5]在扫描的不同点添加候选项集，从而可以动态对项集进行评估，进一步减少数据库扫描次数.陈江平等[6]引入概率的方法对Apriori算法进行改进；黄建明等[7]将数据库转换为十字链表的方式存储，使得扫描数据库的次数减少到了1次；刘维晓等[8]在Apriori中加入用户兴趣项进行改进，从而大范围缩减数据库容量.

1.2M-Apriori算法

Apriori算法中，为了产生频繁k项集，需要保持大量候选项集，特别是当支持度很小的时候.因此，为了减少在扫描数据库确定频繁项集上花费的时间，M-Apriori算法[9]提出了一种新的改进的思路.在第1次扫描数据库时，M-Apriori算法保存频繁1项集L1中的每个项、对应的支持度及每个项所出现的事务ID号的集合.在计算k项集支持度时，M-Apriori算法先将k项集划分为k个1项集；接着，根据频繁1项集L1比较这k个1项集的支持度大小；最后，选择从其中支持度最小的事务ID集合所对应的事务中扫描计算此k项集的支持度，从而大大减少扫描数据库次数.改进后MR-Apriori算法示例，如图1所示.

图1中：D为原始数据库；L1为M-Apriori算法得到频繁1项集结果；实线为删去事务中单个项；虚线为删除整条事务.要产生频繁2项集{I1,I2}，先比较I1和I2的支持度的大小，I1的支持度为5，小于I2的支持度7，扫描从I1所对应的事务ID集合{T1,T3,T7,T9,T10}所对应的事务T1,T3,T7,T9,T10，计算{I1,I2}的支持度，这样本来需要扫描整个数据库，现在只用扫描其中的5条，减少了扫描次数.同理，要产生频繁3项集{I1,I2,I3}时，比较I1,I2和I3的支持度，扫描从支持度最小的即I1所对应的事务ID集合{T1,T3,T7,T9,T10}所对应的事务T1,T3,T7,T9,T10，计算{I1,I2,I3}的支持度.

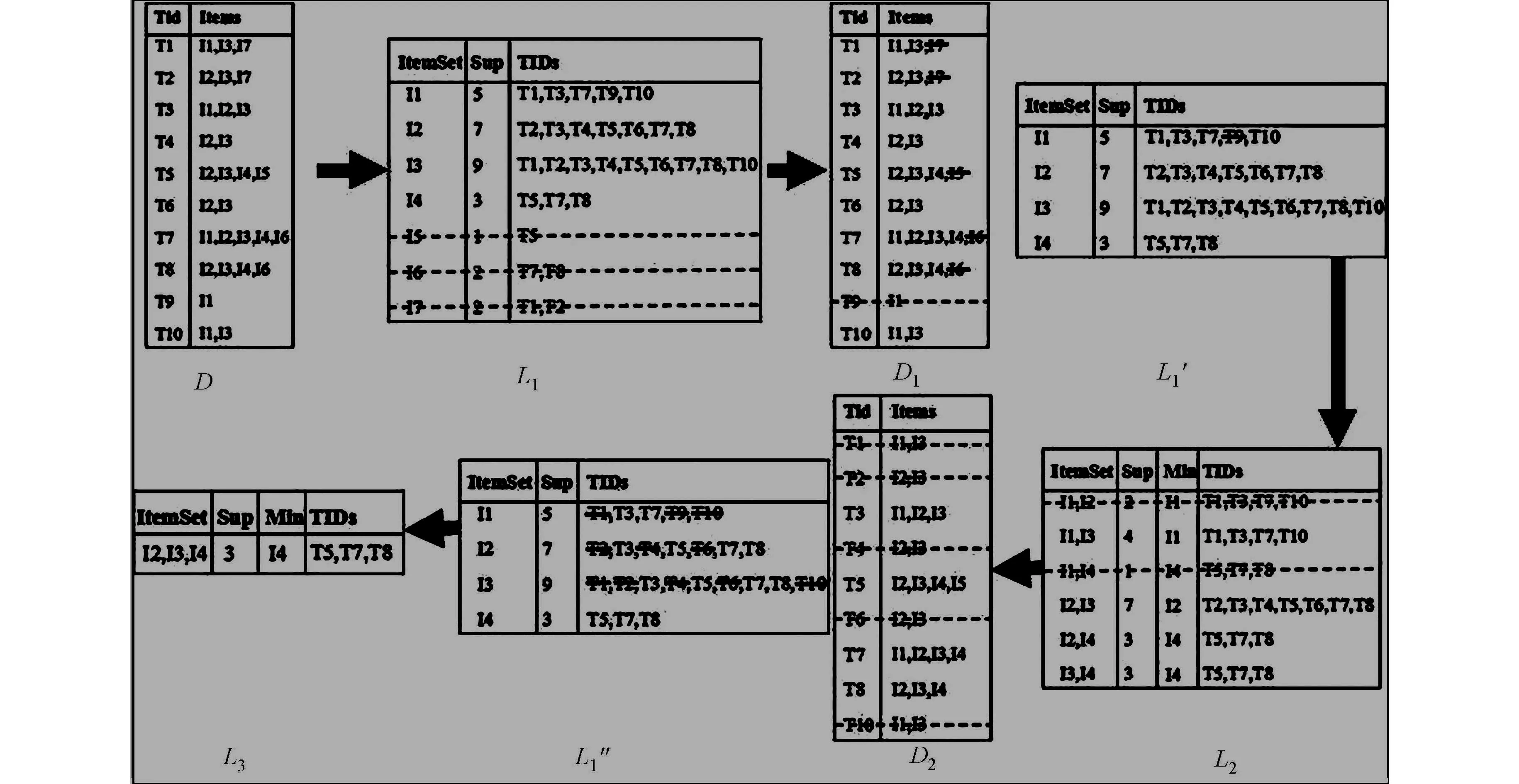
图1 改进后MR-Apriori算法示例Fig.1 Example of improved MR-Apriori algorithm

2 M-Apriori算法的优化

2.1MR-Apriori算法

文献[10]为了改进Apriori算法，用两点优化(性质1，2)：从数据库中删除某个值；删除某条事务.

性质1当扫描第k(k≥2)次时，从数据库中删除在频繁k-1项集Lk-1，但不删除在频繁k项集Lk的项.

性质2如果扫描第k(k≥2)次时，某事务项目数小于k, 则可以将其从数据库中删除.

需要注意这两点优化是在第k(k≥2)次扫描时结合在一起作用的，且有先后顺序，先用性质1删除单个项，再判断修改后的数据库中各项事务长度是否小于k(k≥2)，删除小于k(k≥2)的事务.

将这两点优化加入到M-Apriori中，提出MR-Apriori算法.MR-Apriori算法在M-Apriori算法的基础上，加入事务约简技术.在M-Apriori算法扫描数据库前，分别判断性质1，2是否成立，从而对数据库进行约简.然后，在约简后的数据库上执行M-Apriori算法的后续步骤.为了计算k项集支持度，根据频繁1项集L1比较k个1项集的支持度大小，扫描支持度最小的事务ID集合所对应的事务中，计算k项集的支持度.保存频繁1项集L1中的每个项，每个项对应的支持度及每个项所出现的事务ID号的集合，由于MR-Apriori算法对事务进行了约简，相应的L1的事务ID号集合这一项也要相应修改.

2.2MP-Apriori算法

Apriori算法产生大量候选集，尤其是候选2项集.候选集需要剪枝步骤才能生成频繁项集，M-Apriori算法采用的还是Apriori算法的剪枝原理，即∀c∈Ck，判断c的k个(k-1)-子集是否都在Lk-1中，若找到一个(k-1)-子集不在Lk-1中就淘汰c.因为这个过程会多次扫描Lk-1，特别是当生成Ck很大时，算法的效率并不理想[12].优化1虽然约简数据库，也能一定程度上由于数据库的减少而使生成的候选集数目减少，但从本质上说仍是基于传统Apriori算法的剪枝原理产生候选集，并没有充分改进候选集的剪枝过程.

定义matrix[MaxItemId][MaxItemId]的2项集支持度矩阵是一个三角矩阵(全部元素位于次对角线上方)，其中，MaxItemId为数据库中所有项的最大值，MaxItemId 为7，矩阵初始元素全部为0.MP-Apriori算法有如下3个步骤.

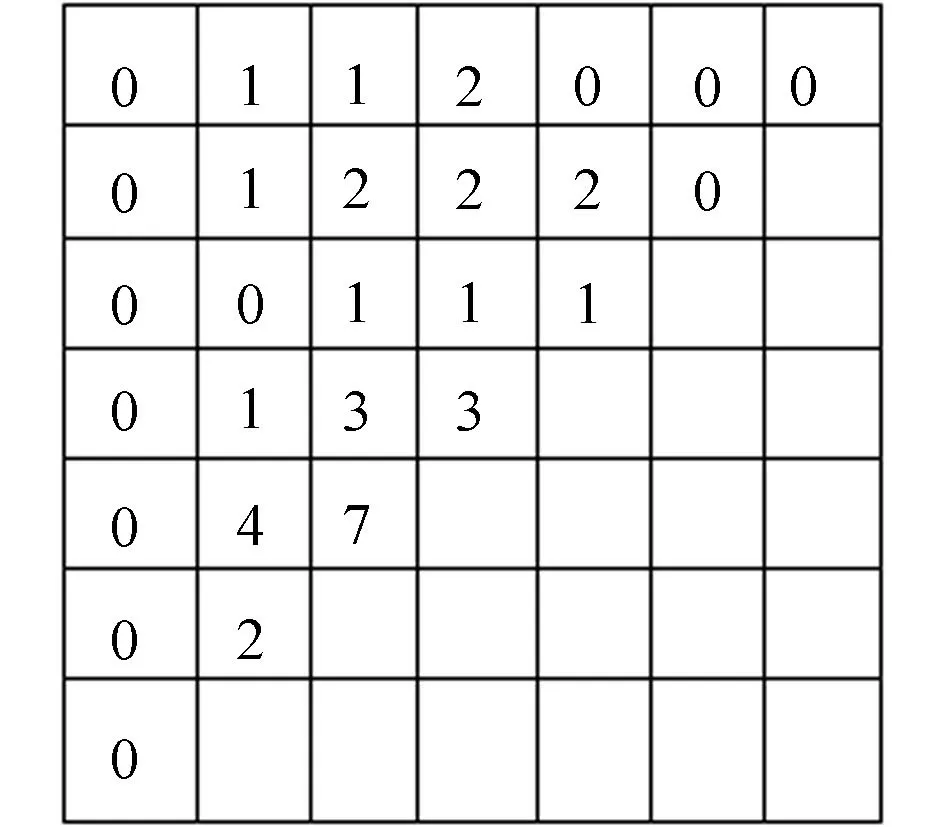
图2 填充后2项集支持度矩阵Fig.2 Two item support matrix after being filled

步骤1扫描数据库，构造2项集的支持度矩阵.以数据库中的项作为矩阵相应的行标和列标，如果扫描到一条事务中包含有{Ii,Ij}2项集，则对矩阵进行一次填充.

矩阵元素填充规则为：如果行下标i小于列下标j，则matrix[MaxItemId-j][i]+=1；否则，matrix[MaxItemId -1][j]+=1.填充后2项集支持度矩阵，如图2所示.

步骤2产生频繁2项集，由于第一步已经用矩阵保存了2项集和其对应的支持度，因此，只需要连接频繁1项集L1和频繁1项集L1.然后，从矩阵中得到连接后得到2项集的支持度，若支持度大于等于最小支持度，则加入到频繁2项集中.获取元素值的方法为：如果行下标i小于列下标j，则对应元素值为matrix[maxItemId -j][i]位置的值；否则，为matrix[maxItemId-1][j]位置的值.

步骤3产生频繁k(k≥3)项集,和M-Apriori算法中步骤基本一致，唯一不同的就是在算法的剪枝步.在M-Apriori算法中的剪枝步骤，要不断扫描数据库，确定候选k项集Ck的每一个(k-1)项非空真子集是否都是频繁的，从而确定频繁k项集Lk，而为了运用2项集支持度矩阵对Ck进行快速剪枝，在原剪枝前面加入了一个预判断.方法是在进行原Apriori剪枝前，先将要进行连接的两个项集的各自最后一项进行连接得到二项集；然后，从矩阵中得到该二项集的支持度.如果小于最小支持度，可以把两个连接的候选项集的连接项剪掉.通过这样的预先判断，只有矩阵元素的值大于等于最小支持度时，才需要检查此连接项的所有(k-1)项子集是否都是频繁的，从而可以大大提高算法效率.

2.3MRP-Apriori算法

优化1，2从两个不同的方向对M-Apriori算法进行优化改进，MRP-Apriori算法将优化1，2综合到一起加入到M-Apriori算法中.

3 实验结果与分析

图3 不同支持度下的运行时间对比Fig.3 Comparation of running time in different support

实验平台为Intel(R) Core(TM) i5-3470，主频为3.20 GHz；内存为8 GB，Windows 7 旗舰版 64位 SP1.采用的编程语言为Java，开发环境为Eclipse 4.4.0.实验数据集为fimi网站([ http:∥fimi.ua.ac.be/ ])上的蘑菇数据集，它共有8 124条事务，119个属性，事务平均长度为23项.不同支持度下的运行时间对比，如图3所示.图3中：t为运行时间；ηmin为最小支持度.由图3可知：MR-Apriori算法由于对在M-Apriori算法的基础上加入事务约简，使得运行效率较M-Apriori算法有所提高.MP-Apriori算法引进了2项集支持度矩阵，虽然需要消耗一定的存储空间，但是它的效率提高比较明显，比较显著地提高算法的效率.MRP-Apriori算法则综合了以上两个算法的优点，因此，它的效率是最高的.

4 结论

在改进的M-Apriori算法，加入了事务约简优化，提出MR-Apriori算法，在算法计算候选项集支持度时减少了原数据库中记录的数目，从而进一步减少了数据库的次数，提高算法的效率.扫描加入了2项集支持度矩阵快速剪枝优化，能快速对候选项目集进行快速剪枝，而不用像原算法那样需要检查候选k项集的所有(k-1)项子集是否都是频繁的，从而提高了效率.最后，结合前两点优化，把提高效率的这两方面结合到一起，提出了MRP-Apriori算法，再用实验验证了这3种算法的效率.

然而，第1点优化会对数据库进行修改，需要花费精力对数据库进行维护，降低算法效率.下一步将考虑使用其他办法减少数据库扫描次数，或在编写代码时，设置标志位，跳过这些需要被删除的事务，而不是直接将其删去，从而提高效率.第2点优化中，当数据库事务平均长度很大时，矩阵会迅速增大，还可能会存在大量的零元素，从而会对算法效率有所影响.下一步将对此问题的改进方法进行研究.

[1] AGRAWAL R,SRIKANT R.Fast algorithms for mining association rules[C]∥Proc 20th Int Conf Very Large Data Bases.Santiago：VLDB,1994:487-499.

[2] PARK J S, CHEN M S, YU P S.An effective hash-based algorithm for mining association rules[J].ACM,1995：175-186.

[3] SAVASERE A,OMIECINSKI E R,NAVATHE S B.An efficient algorithm for mining association rules in large databases[C]∥ International Conference on Very Large Data Bases.[S.l.]:Morgan Kaufmann Publishers Inc,1995:432-444.

[4] TOIVONEN H.Sampling large databases for association rules[C]∥Proceedings of the 22nd VLDB Conference.Mumbai：[s.n.],1996:134-145.

[5] BRIN S,MOTWANI R,ULLMAN J D,etal.Dynamic itemset counting and implication rules for market basket data[J].ACM SIGMOD Record,1997,26(2):255-264.

[6] 陈江平,傅仲良,徐志红.一种Apriori的改进算法[J].武汉大学学报(信息科学版),2003,28(1):94-99.

[7] 黄建明,赵文静,王星星.基于十字链表的Apriori改进算法[J].计算机工程,2009,35(2):37-38,40.

[8] 刘维晓,陈俊丽,屈世富,等.一种改进的Apriori算法[J].计算机工程与应用,2011,47(11):149-159.

[9] AL-MAOLEGI M,ARKOK B.An improved apriori algorithm for association rules[J].International Journal on Natural Language Computing,2014,3(1):21-29.

[10] SINGH J,RAM H,SODHI D J S.Improving efficiency of apriori algorithm using transaction reduction[J].International Journal of Scientific and Research Publications,2013,3(1):1-4.

[11] 纪怀猛.基于频繁2项集支持矩阵的Apriori改进算法[J].计算机工程,2013,39(11):183-186.

[12] 胡吉明,鲜学丰.挖掘关联规则中Apriori算法的研究与改进[J].计算机技术与发展,2006,16(4):99-101.

(责任编辑： 陈志贤英文审校： 吴逢铁)

ImprovedAprioriAlgorithmforQuicklyPrunebyCombiningTransactionReductionWithTwo-ItemSetSupportMatrix

ZHANG Jian， LIU Shaotao

(College of Computer Science and Technology, Huaqiao University, Xiamen 361021, China)

10.11830/ISSN.1000-5013.201510043

2015-10-21

刘韶涛(1969-)，男，副教授，主要从事软件体系结构与软件复用的研究.E-mail:shaotaol@hqu.edu.cn.

福建省科技计划重大项目(2011H6016)

TP 311

A

1000-5013(2017)05-0727-05