采用轴棱锥检测涡旋光束拓扑电荷数的方法

胡润， 吴逢铁， 杨艳飞

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 华侨大学 福建省光传输与变换重点实验室， 福建 厦门 361021)

采用轴棱锥检测涡旋光束拓扑电荷数的方法

胡润1,2， 吴逢铁1,2， 杨艳飞1,2

(1. 华侨大学 信息科学与工程学院， 福建 厦门 361021;2. 华侨大学 福建省光传输与变换重点实验室， 福建 厦门 361021)

基于基尔霍夫衍射积分理论，分别推导涡旋光斜入射轴棱锥与凸透镜后的衍射光场表达式.提出一种利用轴棱锥检测光束拓扑电荷数信息的简单可行方案，并将此方案与凸透镜聚焦斜入射涡旋光方案进行对比.研究结果表明：应用轴棱锥聚焦斜入射涡旋光检测拓扑电荷数信息的方式无需对检测点进行严格定标，实际检测工作中该方案更具备灵活性，适用性也更为广泛.通过对设计实验进行验证，实验与理论基本吻合.

衍射积分理论； 涡旋光； 轴棱锥； 拓扑电荷数

Abstract： Based on Kirchhoff diffraction integral theory， the expressions of diffraction field after the axicon and convex lens that illuminated by an oblique vortex beam are derived. A simple and feasible method for detecting topological charge number by using an axicon is proposed. We compare this method with that of using convex lens， results show that there is no need to fix detection point strictly by using an axicon. In practice， this method shows more flexibility and applicability. Experiments are designed to verify the researches. Experimental results are in good agreement with theoretical predictions and numerical simulation.

Keywords： diffraction integral theory； vortex beam； axicon； topological charge number

涡旋光是一种具有螺旋波前且中心光强为零的空心光束,在光学测量[1-2]、量子信息编码[3]、粒子旋转与操纵[4]、图像处理等领域[5-6]具有非常重要的应用价值，一直是研究的热门课题.目前产生涡旋光的方法,主要有计算全息法、空间光调制器法、螺旋相位板法,以及几何光学模式转换法等.相应的对于涡旋光拓扑电荷数的测量方法也大致可分为：Mach-Zehnder干涉法[7]、计算全息图法[8]、涡旋光与平面波干涉法、杨氏双缝干涉法[9]等.2013年,Vaity等[10]提出利用凸透镜聚焦斜入射涡旋光的方式对涡旋光拓扑电荷数进行检测.此方法虽然简单可靠，但是由于凸透镜本身具备的点聚焦特性，致使携带拓扑电荷数信息的衍射光斑图仅出现在凸透镜焦点位置.因此，应用此法进行涡旋光拓扑电荷数检测时，需要对检测点的位置进行严格定标.轴棱锥[11]是一种用于产生无衍射贝塞尔光束的透镜元件.由于其自身所具备的众多优点而迅速得到了广泛的关注与应用，目前对其应用已深入到光学领域的众多方向[12-13].轴棱锥与凸透镜的最大区别在于，轴棱锥具有线聚焦特性[14].鉴于此特性，本文提出一种利用轴棱锥检测涡旋光束拓扑电荷数的简单可行方案,并将此方案与文献[10]中的方案进行对比.

1 理论分析

1.1轴棱锥聚焦斜入射涡旋光

由于光束的斜入射，此时的入射光场[15]可表示为

式(1)中：m为拓扑电荷数；η为光束斜入射角；A0=1.

由基尔霍夫衍射积分理论可知衍射光场为

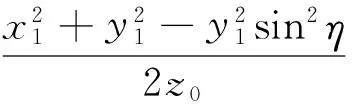
将式(3)代入式(2)，并转换为柱坐标系，有

运用Jacobi-Anger级数展开，可得

根据稳相法原理，可以得到最终衍射光场解析式为

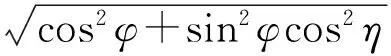
1.2凸透镜聚焦斜入射涡旋光

将式(3)代入上式，运用式(5)，经过化简整理可得凸透镜后的衍射光场为

式(9)中：D为光阑直径.因此，可得光强表达式为

2 数值模拟与讨论

根据式(8),(11)，采用的软件为MathCAD,分别对轴棱锥和凸透镜聚焦斜入射涡旋光的衍射光场进行数值模拟,如图1，2所示.图1,2中：m=3；η=9°；光源采用He-Ne激光器；λ=632.8 nm；光阑直径D=10 mm；元件折射率n=1.458；轴棱锥底角γ=1°；凸透镜焦距f=100 mm.

(a) z=200 mm (b) z=220 mm (c) z=240 mm (d) z=260 mm (e) z=280 mm (f) z=300 mm (g) z=320 mm图1 轴棱锥聚焦斜入射涡旋光后的衍射光斑数值模拟图Fig.1 Simulation results for diffraction patterns after axicon illuminated by oblique vortex beams

(a) z=70 mm (b) z=80 mm (c) z=90 mm (d) z=100 mm (e) z=110 mm (f) z=120 mm (g) z=130 mm图2 凸透镜聚焦斜入射涡旋光后的衍射光斑数值模拟图Fig.2 Simulation results for diffraction patterns after convex lens illuminated by oblique vortex beams

对比图1,2可知：应用轴棱锥和凸透镜聚焦斜入射涡旋光均可得到含有光束拓扑电荷数信息的衍射光斑图.但不同的是，应用轴棱锥聚焦后所得到的衍射光斑图在较长一段距离范围内均携带光束拓扑电荷数信息，而应用凸透镜所得到的衍射光斑图仅在透镜焦距处展现出光束拓扑电荷数信息.因此，在应用透镜聚焦的检测方式时，需要对检测面进行严格定标.由此可以看出，应用轴棱锥聚焦斜入射涡旋光进行拓扑电荷数检测的方式在实际工作中更具备灵活性，适用性也更为广泛.

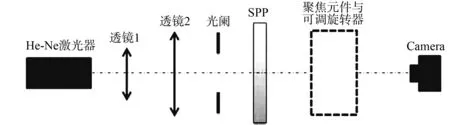
图3 实验装置图Fig.3 Experimental setup

3 实验验证

根据图3进行光路搭建,其中，虚线框内聚焦元件为轴棱锥或凸透镜，可调旋转器实现对聚焦器件的旋转，促使光束斜入射聚焦元件.实验中应用螺旋相位板(SPP)产生涡旋光；透镜1，透镜2的焦距分别为15，190 mm，双透镜组成望远镜系统实现对光源的准直扩束;其他器件参数均与数值模拟中所取参数一致.利用相机分别拍摄到了两组与数值模拟相对应的实验光斑图，如图4，5所示.图4,5中：m=3;η=9°.

(a) z=200 mm (b) z=220 mm (c) z=240 mm (d) z=260 mm (e) z=280 mm (f) z=300 mm (g) z=320 mm图4 轴棱锥聚焦斜入射涡旋光后的实验光斑图Fig.4 Experimental diffraction patterns after axicon illuminated by oblique vortex beams

(a) z=70 mm (b) z=80 mm (c) z=90 mm (d) z=100 mm (e) z=110 mm (f) z=120 mm (g) z=130 mm图5 凸透镜聚焦斜入射涡旋光后的实验光斑图Fig.5 Experimental diffraction patterns after convex lens illuminated by oblique vortex beams

分别对比图1,3和图2,4可以看到，实验结果与数值模拟结果基本一致.对于实验与模拟出现偏差的主要原因有以下2种：1) 准直扩束出的光束并非严格意义上的平行光束，因此，斜入射凸透镜的涡旋光具有一定的发散角或会聚角;2) 器件的误差加工也会造成理论与实验出现差距.此外，由于测距的不精准性，也会造成实验的观察距离与理论模拟的观察距离存在差异.

4 结束语

基于基尔霍夫衍射积分理论，分别推导了涡旋光斜入射轴棱锥与凸透镜后的衍射光场表达式.通过理论与实验的相互佐证，提出一种利用轴棱锥检测光束拓扑电荷数信息的简单可行方案.研究结果表明，相比于凸透镜的定标检测方式，轴棱锥聚焦斜入射涡旋光检测拓扑电荷数的方式无需对检测点进行严格定标，应用起来也更加的灵活便利.文中所得的研究结果虽然是针对相干光源，但同样能拓展至部分相干光，对拓扑电荷数检测工作与轴棱锥的应用具有指导意义.

[1] LI Xinzhong,TAI Yuping,NIE Zhaogang.Digital speckle correlation method based on phase vortices[J].Optical Engineering，2012，51(7):077004.DOI:10.1117/1.OE.51.7.077004.

[2] LI Xinzhong,TAI Yuping,ZHANG Liping,etal.Characterization of dynamic random process using optical vortex metrology[J].Applied Physics B，2014，116(4):901-909.DOI:10.1007/s00340-014-5776-3.

[3] BOZINOVIC N，YUE Y，REN Y，etal.Terabit-scale orbital angular momentum mode division multiplexing in fibers[J].Science，2013，340(6140):1545-1548.DOI:10.1126/science.1237861.

[4] 屈檀，吴振森，韦尹煜,等.拉盖尔高斯涡旋光束对生物细胞的散射特性分析[J].光学学报，2015，35(增刊1):s129002.DOI:10.3788/AOS201535.s129002.

[5] 葛筱璐，王本义，国承山.涡旋光束在湍流大气中的光束扩展[J].光学学报，2016，36(3):0301002.DOI:10.3788/AOS201636.0301002.

[6] 孙喜博，耿远超，刘兰琴,等.弯曲阶跃型光纤中光学涡旋的传输特性研究[J].光学学报，2015，35(增刊1): s106001.DOI:10.3788/AOS201535.s106001.

[7] LEACH J，PADGETT M J，BARNETT S M，etal.Measuring the orbital angular momentum of a single photon[J].Physical Review Letters，2002，88(25):257901.DOI: 10.1103/PhysRevLett.88.257901.

[8] MAIR A，VAZIRI A，WEIHS G，etal.Entanglement of the orbital angular momentum states of photons[J].Nature，2001，412(6844):313-316.DOI:10.1038/35085529.

[9] SZTUL H I，ALFANO R R.Double-slit interference with Laguerre-Gaussian beams[J].Optics Letters，2006，31(7):999-1001.DOI:10.1364/OL.31.000999.

[10] VAITY P，BANERJI J，SINGH R P.Measuring the topological charge of an optical vortex by using a tilted convex lens[J].Physics Letters A，2013，377(15):1154-1156.DOI:10.1016/j.physleta.2013.02.030.

[11] 朱清智，吴逢铁，何西.轴棱锥聚焦贝塞尔-谢尔模型光束产生空心光束[J].光学学报，2016,36(10)：475-480.DOI:10.3788/AOS201636.1026022.

[12] NICHOLSON J W，DESANTOLO A，WESTBROOK P S，etal.Axicons for mode conversion in high peak power， higher-order mode， fiber amplifiers[J].Optics Express，2015，23(26):33849-33860.DOI:10.1364/OE.23.033849.

[13] 陈姿言，胡威旺，吴逢铁，等.无衍射光束提高成像系统分辨率[J].光子学报，2016，45(5):116-120.DOI:10.3788/gzxb20164505.0511002.

[14] 杜团结，王涛，吴逢铁.轴棱锥对无衍射光束的线聚焦特性[J].物理学报，2013，62(13):134103.DOI:10.7498/APS.62.134103.

[15] THAMING A，JAROSZEWICZ Z，FRIBERG A T.Diffractive axicons in oblique illumination: Analysis and experiments and comparison with elliptical axicons[J].Applied Optics，2003，42(1)：9-17.DOI:10.1364/AO.42.000009.

(责任编辑： 钱筠英文审校： 吴逢铁)

MethodsforDetectingTopologicalChargeNumberofVortexBeamsUsingAxicon

HU Run1,2， WU Fengtie1,2， YANG Yanfei1,2

(1. College of Information Science and Engineering， Huaqiao University， Xiamen 361021， China;2. Fujian Key Laboratory of Optical Beam Transmission and Transformation， Huaqiao University， Xiamen 361021， China)

10.11830/ISSN.1000-5013.201703076

2017-03-29

吴逢铁(1958-)，男，教授，博士，主要从事光束传输与变换、短脉冲技术及非线性光学等方面的研究.E-mail:fengtie@hqu.edu.cn.

国家自然科学青年基金资助项目(61605049)； 福建省科技计划重大项目(2016H6016)

O 436.1

A

1000-5013(2017)05-0706-04