利用Mach-Zehnder点衍射干涉仪的激光复振幅实时重建方法

杜永兆

(华侨大学 工学院， 福建 泉州 362021)

利用Mach-Zehnder点衍射干涉仪的激光复振幅实时重建方法

杜永兆

(华侨大学 工学院， 福建 泉州 362021)

在充分利用Mach-Zehnder自参考干涉系统无需设置专门参考光优点的基础上，提出一种激光复振幅实时重建方法.在参考臂和测试臂上分别设置放大倍率为s且互为倒置的望远镜系统，使得经针孔滤波、准直后的参考光被放大s2倍形成波前与振幅(或强度)皆近似于一个平面的理想参考光.研究表明：利用傅里叶分析法从干涉图中便可直接重建待测激光复振幅分布，具有结构简单和测量快速的优点.基于该系统分别对静态和动态输出光场进行复振幅重建实验，并由此求得相应的M2因子，从而验证该方法在复杂光场光束质量实时检测的可行性.

激光光束质量； 复振幅重建； 点衍射干涉仪；M2因子

Abstract： Considering the advantagesof the characteristicssaid as without a special reference wave of Mach-Zehnder point diffraction interference system (MZ-PDI), a real-time complex amplitude reconstruction method is presented. Two telescopes with the magnification s are placed at the reference arm and test arm in MZ-PDI, respectively. The telescope in one arm is inverted with respect to the other one. The reference wave is enlargedS=s2times after filteredby thepinhole filter, consequently, both of the reference wavefrontphaseand reference amplitude (or intensity profile) can be approximately seen as a plane and it services as an ideal reference wave. Thenthe complex amplitude of the test beam can be directly extracted from a single interferogram using the Fourier transform fringe analysis method. The proposed method can provide a simple and fast solutionwhile still maintains high accuracy for reconstructing complex amplitude. The experiments of the static and dynamic output optical wave are demonstrated based on the proposed MZ-PDI system, meanwhile the beam qualityM2factor of the test beam are obtained from the reconstructed complex amplitude. The experimental results showed that feasibility of the proposed system for real-time beam characterization of the complex optical beams.

Keywords： laser beam quality; complex amplitude reconstruction; point diffraction interferometer;M2 factor

为了研究高能激光系统的性能，保证系统的安全运行，同时为光束实时控制提供有效反馈数据，必须对高能激光输出光场全场信息即相位和振幅(或强度)分布进行快速、准确检测.通常的做法是利用波前传感器，如哈特曼-夏克波前传感器[1-2]、曲率波前传感器(CWFS)[3-4]、锥波前传感器(PWFS)[5-7]或自参考干涉波前传感器(SRI-WFS)[8-12]对输出光场的波前相位进行检测；而强度分布则由光电探测器(如CCD)测量得到.但这种相互独立的测量方法不仅增加了测量系统的复杂性，也减低了测量的可靠性与准确性.激光研究人员在如何实现单次便可获得激光输出光场全场信息上做了大量工作.美国的劳伦斯利弗莫尔国家实验室Beamlet装置和英国的AWE实验室Helen 装置分别采用径向剪切干涉仪(RSI)对输出光场的全场分布进行综合检测[13-14].理论上，利用RSI波前相位和振幅迭代重建算法从单幅干涉图中便可重建待测激光的复振幅[15-18]，但因为波前相位和振幅迭代重建算法较为复杂，使得该方法只局限于静态或者是瞬态[18]光场的检测应用.此外，Fuente等[19-21]提出了利用马赫-曾德衍射光束干涉仪(DBI)通过多次数值迭代重建待测激光复振幅的方法，并进行了初步的实验研究，但同样的也受到运算速度的限制.本文提出一种基于改进Mach-Zehnder点衍射干涉仪(MZ-PDI)的激光复振幅实时重建方法，仅需单幅干涉图便可以直接重建待测激光复振幅.

图1 MZ-PDI光路原理图Fig.1 Principle diagram of MZ-PDI

1 MZ-PDI激光复振幅重建的理论分析

1.1MZ-PDI基本原理

为了克服传统SRI-WFS[8-12，22-23]无法一次性获得激光复振幅信息和RSI[15-17]，需要多次迭代计算方可重建激光复振幅分布的缺点，构建了如图1所示的MZ-PDI基本光路结构.在系统的两臂上分别设置放大倍率一致且互为倒置的望远镜系统，使得待测激光进入MZ-PDI系统经分光镜1后分为两束.其中，一束经过由焦距分别为f3，f4的透镜3，4组成放大倍率为s=f3/f4的倒置望远镜系统后形成包含待测激光全部信息的缩小光束，作为测试光；另一光束则依次经过透镜1(焦距为f1)、针孔和透镜2(焦距为f1)组成的放大倍率为s=f2/f1针孔滤波系统滤波后形成扩束光束，作为参考光.参考光和信号光经分光镜2会合后并在成像面Pi发生干涉并形成干涉图.

定义S=s2>1为MZ-PDI的放大倍数.当S足够大的时，经针孔滤波、扩束准直后的波前与振幅(或强度)皆可近似于一个平面形成理想的参考光.因此，利用傅里叶分析法[24]得到干涉图的复振幅调制函数[18]即为待测激光复振幅分布.

1.2针孔滤波原理分析

如图1所示，设A(x0，y0)和W(x0，y0)分别为入射激光E(x0，y0)在物面P0上的振幅与波前分布.那么，经分光镜1的入射激光依次通过透镜3,4，所形成的测试光在像平面Pi的复振幅可表示为

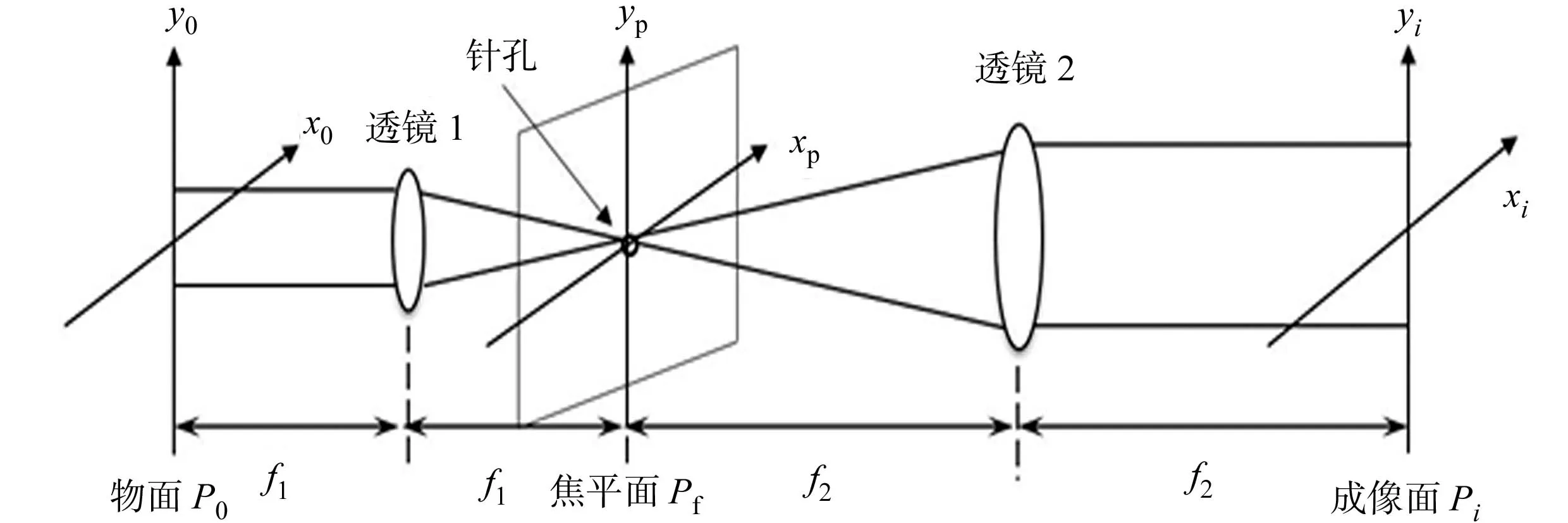
图2 针孔滤波系统示意图Fig.2 Schematic of pinhole filtering system

分光镜1的透射光束则依次通过透镜1，2和针孔组成的针孔滤波系统后，所形成的扩束光束作为参考光.针孔滤波系统可以等效为如图2所示光路系统，其中，针孔放置于透镜1焦平面Pf处，图中相应地标出理论分析过程中需要用到的参数与坐标表达形式.

根据傅里叶光学理论[25]，待测光场E(x0，y0)经透镜1并传播至其焦平面(xp，yp)，相当于对E(x0，y0)作傅里叶变换；焦平面上设置一个直径为dpin的针孔相当于一个理想圆低通滤波器，并对入射光场进行调制实现了低通滤波，即针孔后面的光场可表示为

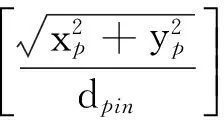
经针孔滤波后的光场Ep(xp，yp)经过透镜2后在其成像面Pi上成像，在数学上相当于对针孔滤波后的光场Ep(xp，yp)再次作傅里叶变换.忽略复比例常数和像的倒置关系，并考虑针孔滤波系统的放大倍率s=f2/f1，且入射光场聚焦在针孔中心，则在成像面Pi上的参考光场为

式(4)中:⊗为二维卷积；T(xi，yi)为针孔滤波窗函数cyl的傅里叶变换，也称为针孔滤波器的脉冲响应函数，其具体表达式[22-23]为

式(5)中:J1为第一类贝塞尔函数.为了便于分析，式(4)所述的参考光场可以写为更一般的形式，即

式(6)中:AR(xi/s，yi/s)和WR(xi/s，yi/s)分别为参考光的振幅和波前.

1.3复振幅重建理论分析

根据光的干涉原理，测试光ET(xi，yi)与参考光ER(xi，yi)在像平面Pi重叠区域发生干涉，其干涉图强度分布可以表示为

式(7)中：κ(xi，yi)=sinθ/λ为参考光与测试光之间夹角θ而引入的线性载频.结合MZ-PDI的特点，把干涉区域(sxi，syi)定义为新的定义域(x，y)，因此，式(7)可以改写为

式(8)中:S=s2为MZ-PDI的放大倍数.式(8)中的第3项可以写成其等价形式，即

定义c(x，y)为干涉图的复振幅调制函数[18]，其具体形式为

当针孔直径dpin足够小时，[2J1(βγ)]/βγ趋近于1，即参考波前WR(x/S，y/S)变成原始波前的积分形式，可近似为一个平面波前；当MZ-PDI的放大倍数S足够大时，参考振幅AR(x/S，y/S)趋近于一个高度为AR(0，0)的平面.考虑到实际应用中考虑振幅的相对值，所得待测激光的复振幅可由以下公式确定，即

干涉图是由线性载频方法得到的，故式(11)容易由傅里叶变换方法[24]得到.根据衍射积分理论[25-26]，由得到的复振幅进一步求得输出光场在其传播方向z上任意位置的光场形式E(x，y，z)，进而得到待测激光光束的相关参数[27]，如束宽、远场发散角及光束质量M2因子等[28]，实现对待测激光光束质量的综合评价.

2 参考光质量仿真与分析

由上述理论分析可知，针孔直径dpin和MZ-PDI放大倍数S是决定MZ-PDI系统能否获得高质量参考光的关键，即其直接关系到 MZ-PDI系统能否精确重建待测激光复振幅分布.

假定待测激光的振幅为1，原始波前相位为峰谷值φPV=2λ的球面波，实际针孔直径大小以针孔滤波系统的艾里斑直径dA为单位.用归一化光强的峰谷值IPV表示参考光强度误差，参考波前的均方根值φRMS表示参考波前精度.不同MZ-PDI系统放大倍数S和针孔直径dpin对针孔滤波后参考光强精度的影响，如图3所示.由图3可知:随着dpin增大，滤波后的参考光强的起伏程度越大；但随着MZ-PDI系统放大倍数S的增大，参考光强的起伏程度则迅速减小.当S=1时，对应的dpin分别为0，5dA，1.0dA，2.0dA和4.0dA时的IPV分别为0.371 4，0.886 6，0.999 2和0.999 9；而当S分别增大到S=3，4，6，8时，对应的dpin滤波后IPV分别减小至0.005 4，0.006 2，0.005 1，0.005 8，几乎接近与一个理想的平面，这与后面的实验结果相符.

(a) dpin=0.5dA (b) dpin=1.0dA

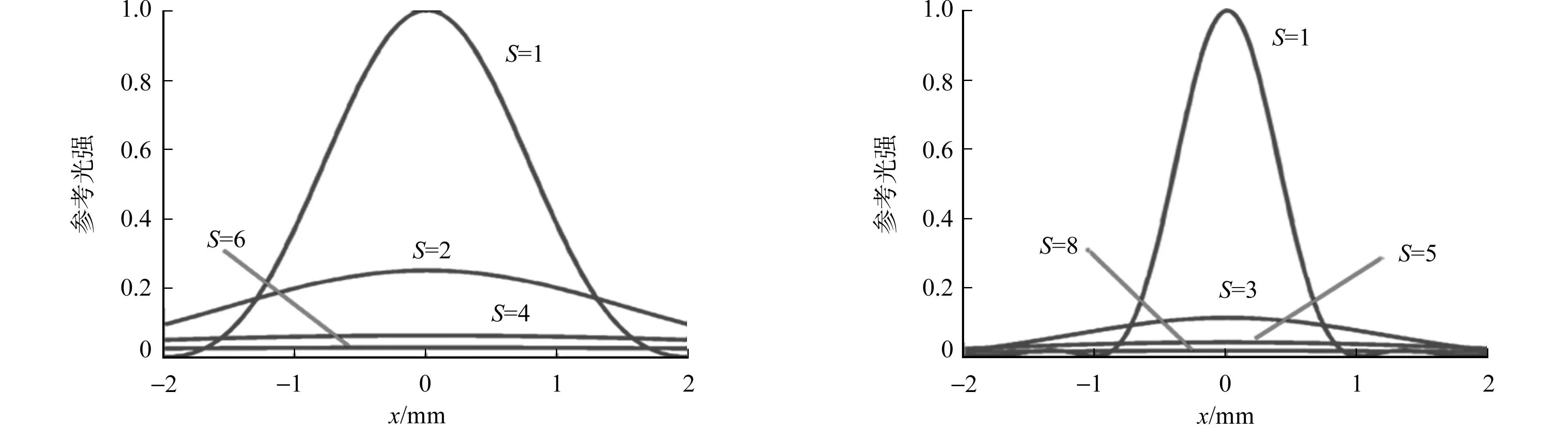
(c) dpin=2.0dA (d) dpin=4.0dA图3 系统放大倍数与针孔直径对参考光强精度的影响Fig.3 Simulation results of magnification and pinhole diameter impact on accuracy of reference beam intensity

图4 系统放大倍数与针孔直径对参考波前精度的影响Fig.4 Simulation results of magnification and pinhole diameter impact on accuracy of reference wavefront phase

不同系统放大倍数与针孔直径对针孔滤波后参考波前精度的影响，如图4所示.由图4可知：随着dpin增大时，参考波前误差φRMS急剧上升；但是随着S的增大，参考波前误差则迅速减小并趋向于一个定值.当dpin=0.5dA且S=1时，φRMS=0.009 1，这与文献[11，22-23]中的结果相符.而当dpin增大为1.0dA，2.0dA和4.0dA后，适当增大S同样可以获得高精度的参考波前，即S=2，4，8分别对应于dpin为1.0dA，2.0dA和4.0dA的φRMS分别为0.009 2λ，0.008 7λ和0.010 2λ，几乎与dpin为0.5dA时的参考波前一致.

由以上分析可知，当增大dpin时，适当增大S不但可以获得高精度的参考光强和参考波前，同时因为增大了dpin也可以提高参考光强度通过率，并且使不同波前像差的光场经针孔滤波后的强度通过率的趋于平稳[11].即增大dpin可以使得干涉图的背景光强和对比度更加的均匀稳定，也因此改善了动态光场复振幅测量时条纹对比度波动问题，使得该系统用于动态光场复振幅实时检测成为可能.

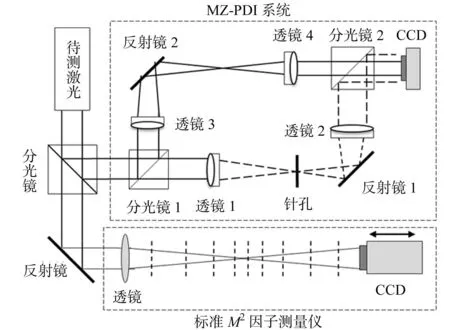
图5 复振幅重建实验装置Fig.5 Complex amplitude reconstruction experimental device

3 实验结果与讨论

为验证所提方案的可行性，对波长为532 nm且可通过微调输出腔镜激发不同阶厄米-高斯混合模的二极管泵浦全固态激光器(DPSSL)的输出光场进行复振幅重建实验，装置如图5所示.图5中：MZ-PDI系统所采用的分光镜1，2为5∶5单波长分光平板；反射镜1，2为532 nm单波长介质膜高反射镜；透镜1，2，3，4分别为焦距f1=f4=100 mm，f2=f3=300 mm的消像差傅里叶透镜，即MZ-PDI系统的S=9，dpin=25 μm(约为艾里斑直径dA的2倍).由此计算相应的M2因子，并与标准M2因子测量仪的测量结果相比较.

实验中，首先微调DPSSL的输出腔镜，使其输出为一个类似于厄米-高斯TEM20模的光场作为待测激光；待测激光经准直放大后进入MZ-PDI复振幅重建系统并被分光镜分为两束.其中,一束经反射镜后进入M2因子测量仪；另一束进入MZ-PDI系统，参考光和测试光经过成像系统后发生干涉.为了得到高对比度的干涉图，实验中需要在MZ-PDI两干涉臂分别放置可调节衰减器，以便获得高对比度的干涉条纹图.最后，干涉图由CCD记录并经数据采集系统送至计算机PC；然后利用傅里叶变换法重建的待测激光复振幅分布，如图6所示.由图6可知：计算得到直接测量光强和实验重建光强分布的互相关系数C(当C=1时说明完全匹配)为0.972，二者吻合得很好.

(a) 采集到的干涉图 (b) 直接测量的强度分布

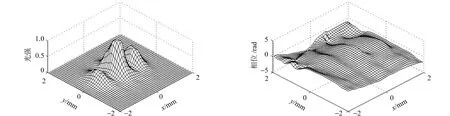
(c) 重建的强度分布 (d) 重建的相位分布图6 复振幅重建实验结果Fig.6 Experiment results of complex amplitude reconstruction

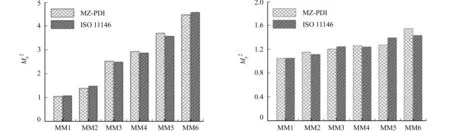
图7 MZ-PDI与标准M2因子测量仪的结果比较Fig.7 Measurement results of beam quality M2 factor with the proposed MZ-PDI method and standard M2 factor measurement instrument

图8 动态光场M2因子随时间变化情况Fig.8 Experimental results of dynamic lightfield M2 factor versus change time

为进一步验证该方法实时检测的可行性，对动态变化光场的复振幅进行在线重建实验.在DPSSL输出光场MM3中引入空气抖动使输出光场呈动态变化，用CCD以8 帧·s-1的速度记录动态干涉图，利用复振幅重建方法重建动态变化的复振幅，对应得到动态光场的M2因子随时间变化情况，如图8所示.由图8可知：该方法能够有效地实时重建瞬态光场的复振幅分布.

4 结束语

结合针孔滤波理论分析基于MZ-PDI复振幅重建方法的基本原理，讨论针孔直径dpin和MZ-PDI放大倍数S对参考光强和参考波前精度及参考光强度通过率的影响.搭建了MZ-PDI激光复振幅实时重建系统，分别对静态和动态光场进行复振幅重建实验，由此求得相应光束质量M2因子.实验结果验证了所提方案在复杂光场的复振幅实时重建的可行性.

[1] BUENO J M,ACOSTA E,SCHWARZ C,etal.Wavefront measurements of phase plates combining a point-diffraction interferometer and a Hartmann-Shack sensor[J].Applied Optics,2010,49(3):450-456.

[2] ZHAO Liping,GUO Wenjiang,LI Xiang,etal.Reference-free Shack-Hartmann wavefront sensor[J].Optics Letters,2011,36(15):2752-2754.

[3] XI Fengjie,JIANG Zongfu,XU Xiaojun,etal.High-diffractive-efficiency defocus grating for wavefront curvature sensing[J].Journal of the Optical Society of America A,2007,24(11):3444-3448.

[4] BURVALL A,DALY E,CHAMOT S R,etal.Linearity of the pyramid wavefront sensor[J].Optics Express,2007,14(25):11925-11934.

[5] LEDUE J,JOLISSAINT L,VERAM J P,etal.Calibration and testing with real turbulence of a pyramid sensor employing static modulation[J].Optics Express,2009,17(9):7186-7195.

[6] DALY E M,DAINTY C.Ophthalmic wavefront measurements using a versatile pyramid sensor[J].Applied Optics,2010,49(31):G68-G77.

[7] WANG Jianxin,BAI Fuzhong,NING Yu,etal.Comparison between non-modulation four-sided and two-sided pyramid wavefront sensor[J].Optics Express,2010,18(26):27534-27549.

[8] FELDMAN M,MOCLDER D J,ENGLISH R E,etal.Self-referencing Mach-Zehnder interferometer as a laser system diagnostic active and adaptive optical systems[C]∥Proceedings of Active and Adaptive Optical Systems.San Diego:SPIE,1991:490-501.

[9] PATERSON C,NOTARAS J.Demonstration of closed-loop adaptive optics with a point-diffraction interferometer in strong scintillation with optical vortices[J].Optics Express,2007,15(21):13745-13756.

[10] NOTARAS J,PATERSON C.Point-diffraction interferometer for atmospheric adaptive optics in strong scintillation[J].Optics Communications,2008,281(3):360-367.

[11] 白福忠,饶长辉.针孔直径对自参考干涉波前传感器测量精度的影响[J].物理学报,2010,59(6):4056-4064.

[12] BAI Fuzhong,RAO Changhui.Experimental validation of closed-loop adaptive optics based on a self-referencing interferometer wavefront sensor and a liquid-crystal spatial light modulator[J].Optics Communications,2010,283(14):2782-2786.

[13] WEGNER P J,HENESIAN M A,SALMON J T,etal.Wavefront and divergence of the Beamlet prototype laser[C]∥International Conference on Solid State Lasers for Application to Inertial Confinement Fusion.Monterey:SPIE,1999:1019-1030.

[14] BARNES A A R,SMITH I C.Combined phase, near field, and far field diagnostic for large-aperture laser systems[C]∥International Conference on Solid State Lasers for Application to Inertial Confinement Fusion.Monterey:SPIE,1999:564-572.

[15] LI Dahai,WEN Fulin,WANG Qionghua,etal.Improved formula of wavefront reconstruction from a radial shearing interferogram[J].Optics Letters,2008,33(3):210-212.

[16] LI Dahai,QI Xiaoping,WANG Qionghua,etal.Accurate retrieval algorithm of amplitude from radial-shearing interferogram [J].Optics Letters,2010,35(18):3054- 3056.

[17] LIU Dong,YANG Yongying,WANG Lin,etal.Real time diagnosis of transient pulse laser with high repetition by radial shearing interferometer[J].Applied Optics,2007,46(34):8305-8314.

[18] LOPEZ L E,DE I F R.Amplitude and phase reconstruction by radial shearing interferometry[J].Applied Optics,2008,47(3):372-377.

[19] FUENTE R D L,LAGO E L.Wavefront sensing by diffracted beam interferometry[J].Journal of Optics A Pure & Applied Optics,2002,4(4):299-302.

[20] FUENTE R D L,LAGO E L.Mach-Zehnder diffracted beam interferometer[J].Optics Express,2007,15(7):3876-3887.

[21] LAGO E L,FUENTE R D L.Single-shot amplitude and phase reconstruction by diffracted-beam interferometry[J].Journal of Optics a Pure & Applied Optics,2009,11(12):802-807.

[22] SMARTT R N,STELL W H.Theory and application of point-diffraction interferometers[J].Japanese Journal of Applied Physics,1975,14(S1):272-274.

[23] MERCER C R,CREATH K.Liquid-crystal point-diffraction interferometer for wave-front measurements[J].Applied Optics,1996,35(10):1633-1642.

[24] TAKEDA M,INA H,KOBAYASHI S.Fourier-transform method of fringe pattern analysis for computer-based topography and interferometry[J].Journal of the Optical Society of America,1982,72(1):156-160.

[25] GOODMAN J W.Introduction to Fourier optics[M].3rd ed.Denver：Roberts and Company Publish,2005：63-90.

[26] MENDLOVIC D,ZALEVSKY Z,KONFORTI N.Computation considerations and fast algorithms for calculating the diffraction integral[J].Journal of Modern Optics,1997,44(2):407-414.

[27] 冯国英,周寿桓.激光光束质量综合评价的探讨[J].中国激光,2009,36(7):1643-1653.

[28] International Standardization for Standardization.Laser and laser-related equipment-test methods for laser beam width, divergence angles and beam propagation ratio part 1,2,3: ISO 11146[S].1st ed.Geneva:ISO Standardization,2005:1-6.

(责任编辑： 黄晓楠英文审校： 吴逢铁)

Real-TimeComplexAmplitudeReconstructionMethodUsingMach-ZehnderPointDiffractionInterferometer

DU Yongzhao

(College of Engineering， Huaqiao University， Quanzhou 362021， China)

10.11830/ISSN.1000-5013.201606119

2016-06-06

杜永兆(1985-)，男，讲师，博士，主要从事激光光束质量评价与测量、光学成像及光电图像处理及应用的研究.E-mail:yongzhaodu@126.com.

国家自然科学青年基金资助项目(61605048)； 福建省自然科学基金面上资助项目(2016J01300)； 福建省科技创新平台资助项目(2013H2002)； 华侨大学高层次人才科研启动项目(600005-Z15Y0073)

TN 401

A

1000-5013(2017)05-0699-07