采用解析模态分解和小波变换的损伤识别方法

刘景良， 高源， 骆勇鹏， 郑文婷

(1. 福建农林大学 交通与土木工程学院， 福建 福州 350002；2. 福建工程学院 土木工程学院， 福建 福州 350118)

采用解析模态分解和小波变换的损伤识别方法

刘景良1， 高源1， 骆勇鹏1， 郑文婷2

(1. 福建农林大学 交通与土木工程学院， 福建 福州 350002；2. 福建工程学院 土木工程学院， 福建 福州 350118)

针对希尔伯特-黄变换(HHT)在信号处理中存在的模态混叠现象，引入解析模态分解定理(AMD)提取时变结构响应的一阶本征函数，并构建一阶本征函数能量比指标识别结构的损伤位置.从损伤位置处的响应信号出发，引入连续小波变换和时间窗思想，提出一阶本征函数小波能量变化率指标来预测结构的损伤演化过程.通过一个刚度突变和线性变化的三层剪切型结构数值算例，对一阶本征函数能量比和一阶本征函数小波能量变化率指标进行验证.结果表明：所提出的指标能够有效识别结构的损伤位置和损伤时间.

损伤识别； 小波变换； 解析模态分解； 一阶本征函数

Abstract： Due to the problem of overlapping frequency existed in Hilbert-Huang transform (HHT)， analytical mode decomposition theorem is introduced to extract the first order intrinsic mode function (IMF) from responses of time-varying structures， then the first order IMF energy ratio index is established to identify damage locations. Based on the response signal in damage location， continuous wavelet transform and time window are introduced to build the index of the first order IMF wavelet energy variation rate in order to predict the evolution of structural damage. A numerical example of three-story shear structure with abruptly and linearly varying stiffness is presented to verify the effectiveness of the two proposed indexes， and the results demonstrate that the proposed damage indexes can effectively detect the locations and time of structure damage.

Keywords： damage detection； wavelet transform； analytical mode decomposition； first order intrinsic mode function

工程结构在服役期间受到不断变化的外加荷载和环境作用时，其损伤不断积累，本质上属于时变和非线性结构系统，其响应信号呈现非平稳性[1].采用信号处理方法识别结构时变损伤时，需要时频的分析工具[2-4].Huang等[5-6]提出的希尔伯特-黄变换(HHT)，通过经验模态分解(EMD)将原始信号分解成一系列本征函数(IMF)，然后,对每一个IMF进行希尔伯特变换,从而实现信号瞬时特征参数的提取.为解决模态叠混问题，Wu等[7]在经验模态分解方法的基础上提出了集合经验模态分解(EEMD).HHT这一类方法虽然能够有效处理非平稳信号，但是该方法本身也存在一定的问题[8].为此，Chen等[9]提出解析模态分解(AMD)定理提取分量信号[10-11].在结构服役期间，损伤位置处响应信号的各组成成分能量在损伤前后通常会发生比较大的变化.因此,可以采用一阶IMF分量信号的能量作为损伤指标来识别结构的损伤位置[12-13].目前，关于时变结构损伤识别方法的研究工作并不多见[14-17].在前人研究的基础上，本文提出基于解析模态分解和小波变换的损伤识别方法，并通过算例对一阶本征函数能量比和一阶本征函数小波能量变化率指标进行验证.

1 基本原理

1.1解析模态分解定理

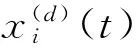
1.2小波变换

小波变换是一种窗口大小固定，形状可以改变的自适应时频分析方法.由于小波变换在时域和频域均具有良好的局部化性质，目前已被广泛应用于信号处理、参数识别与损伤识别等多个领域.

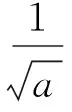
式(1)中:a为尺度因子，与频率成反比关系；b为平移因子，与时间有关.通过改变a和b的值可以实现小波的伸缩和平移.

将任意L2(R)空间的信号x(t)在小波基下展开，即为连续小波变换，其表达式为

2 损伤识别指标

2.1一阶本征函数能量比

在地震作用下，若结构某层出现损伤，可以看做该层发生软化现象从而吸收更多的地震能量，最终导致该层响应的能量相对于其他层的能量增加.因此，可以利用各层一阶本征函数能量比的变化来识别结构的损伤位置.

首先，定义整个地震时间历程内第j层一阶本征函数能量为

式(4)中:IMFj，1为第j层结构响应的一阶IMF分量，可通过AMD定理提取；t1和t2分别为地震波记录的起止时间.

在此基础上，定义第j层一阶本征函数能量比为

式(5)中:n为结构总层数.

2.2一阶本征函数小波能量变化率

实际工程结构的损伤是一个损伤逐渐积累的渐变过程，渐变的损伤过程需要时变损伤指数作为表征.在对损伤位置处一阶IMF分量进行连续小波变换的基础上，引入时间窗思想定义一阶本征函数小波能量变化率(RFOIMFE)为时变损伤指数，该指标仅需已知结构响应信号，即能实现时变损伤的识别.

首先，采用AMD定理提取损伤位置处响应信号的一阶IMF分量，然后，对其进行连续小波变换得到小波系数矩阵W1(ai，bj)m×n.其中：m代表尺度i个数；n为采样时间点bj个数.由于小波尺度与频率存在一一对应关系，按a=(Fc·fs)/fa,可进行频率与尺度之间的转换.其中：a为小波尺度；Fc为小波中心频率；fs为采样频率；fa为尺度a对应的频率.对所有尺度所对应的小波系数进行求和，可得

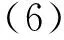
式(6)中:Ws(bj)为求和后的小波系数，是n维行向量.

为追踪结构的时变损伤，在提取各阶IMF分量后，沿求和后的小波系数Ws(ai，bj)曲线设置一个滑动时间窗，窗口长度为2Δt， 以窗内的小波能量平均值代表滑动窗中心点小波能量. 令窗口沿时间轴不

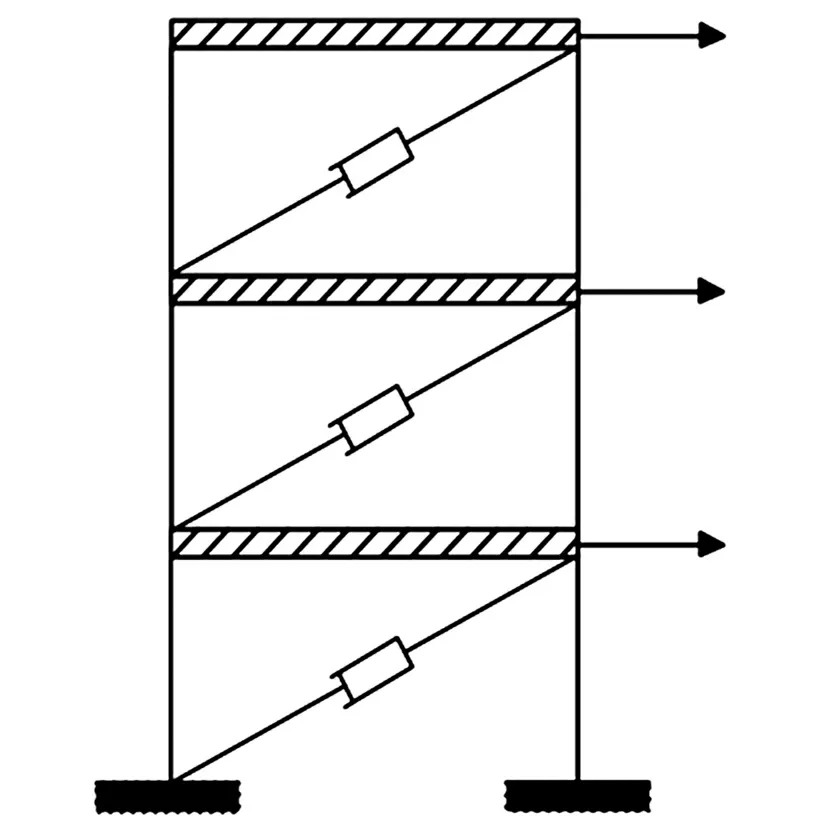
图1 三层剪切型结构模型Fig.1 Three-story shear structure model

断滑动，可求得一阶本征函数小波能量在每个中心点的值，即

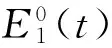
3 数值验证

为验证所提出损伤指标的有效性,以三层剪切型结构模型为例,对刚度突变和线性变化两种损伤工况进行识别.图1为三层剪切型结构模型,表1为主要结构参数.表1中:m为质量;k1为初始刚度;c1为阻尼系数.

表1 三层剪切型结构参数Tab.1 Parameters of three-story shear structure

3.1刚度突变工况下的损伤识别

设定三层剪切型结构某层的刚度发生突变，刚度的折减可以通过降低弹性模量实现，具体的损伤工况如表2所示.结构各层的位移(Δ)响应通过龙格-库塔法求解，其中，采样频率为1 000 Hz，添加的高斯白噪声水平为15%.为简单起见，图2中只给出了DS2工况下结构第一层位移响应.

通过AMD定理提取DS2工况中三层剪切型结构第一层位移响应的一阶分量信号和余量信号，结果如图3所示.同理，可得第二层和第三层位移响应的一阶分量信号和余量信号.在成功提取各层一阶IMF分量信号的基础上，根据式(4),(5)求解一阶本征函数能量比指标rj，如表2所示.

由表2可知：相比DS1工况，即结构完好无损时，DS2工况下第一层位移响应的一阶本征函数能量比值r1相应增加，因此，可以判定剪切型结构的第一层出现了损伤，即发生软化现象，吸收了更多的能量，其结果必然是一阶本征函数能量比值相应增加.同样地，DS6和DS7工况中的损伤指标值r2和r3比DS1工况中的相应值增加.这说明DS6和DS7工况中的损伤位置分别为剪切型结构的第二层和第三层，这与事先设定的损伤情况是完全吻合的.因此,一阶本征函数能量比指标能够准确识别剪切型结构的损伤位置.

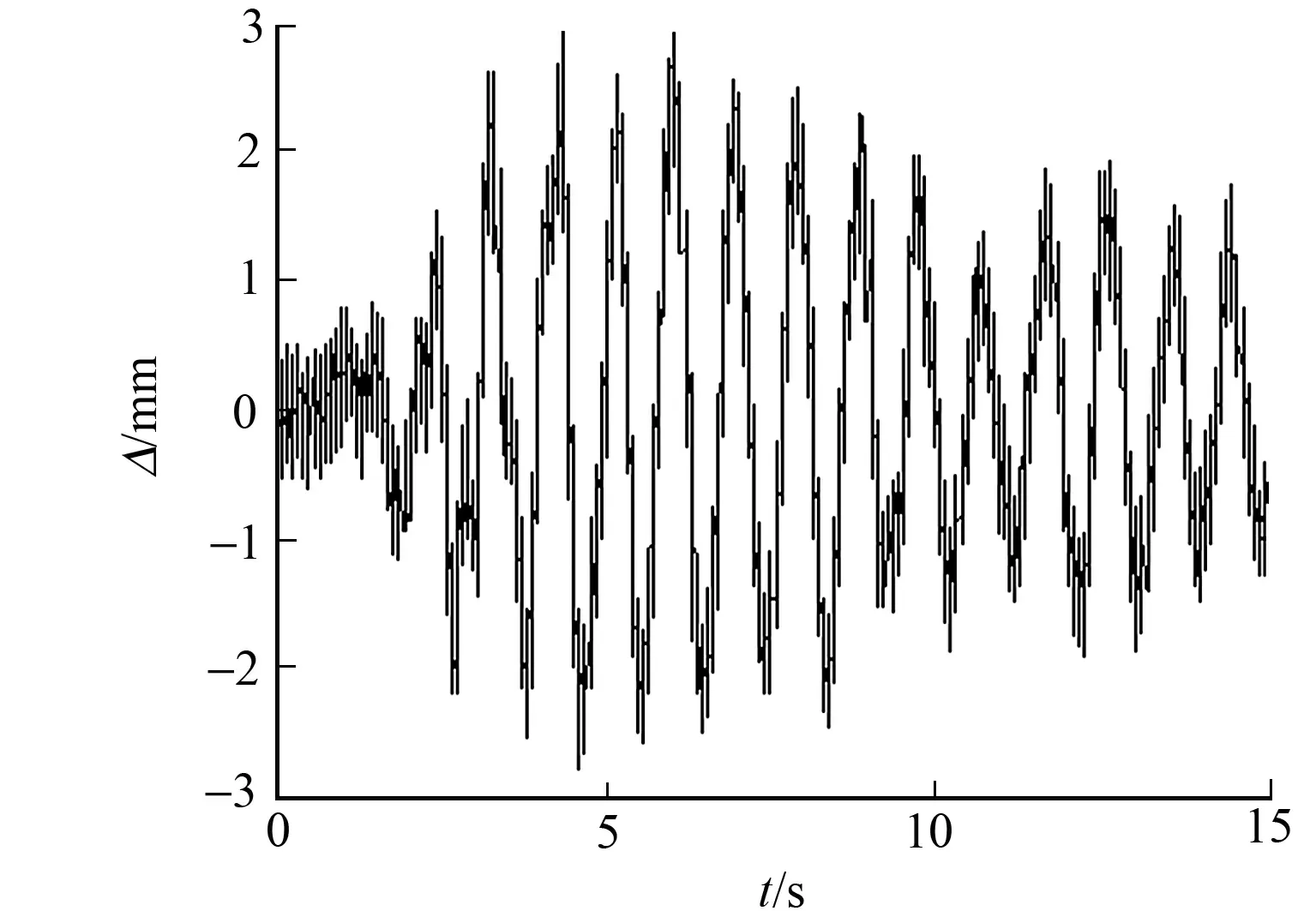
图2 DS2工况下结构第一层位移响应 Fig.2 Displacement responses of first story under DS2 cases

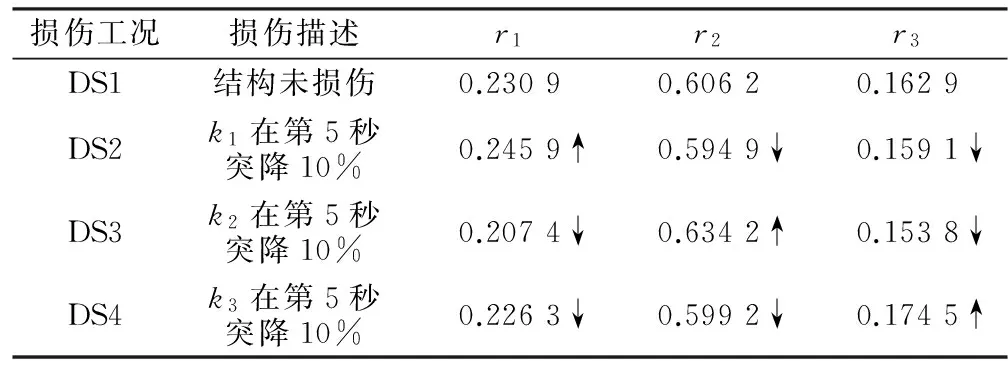
损伤工况损伤描述r1r2r3DS1结构未损伤0.23090.60620.1629DS2k1在第5秒突降10%0.2459↑0.5949↓0.1591↓DS3k2在第5秒突降10%0.2074↓0.6342↑0.1538↓DS4k3在第5秒突降10%0.2263↓0.5992↓0.1745↑

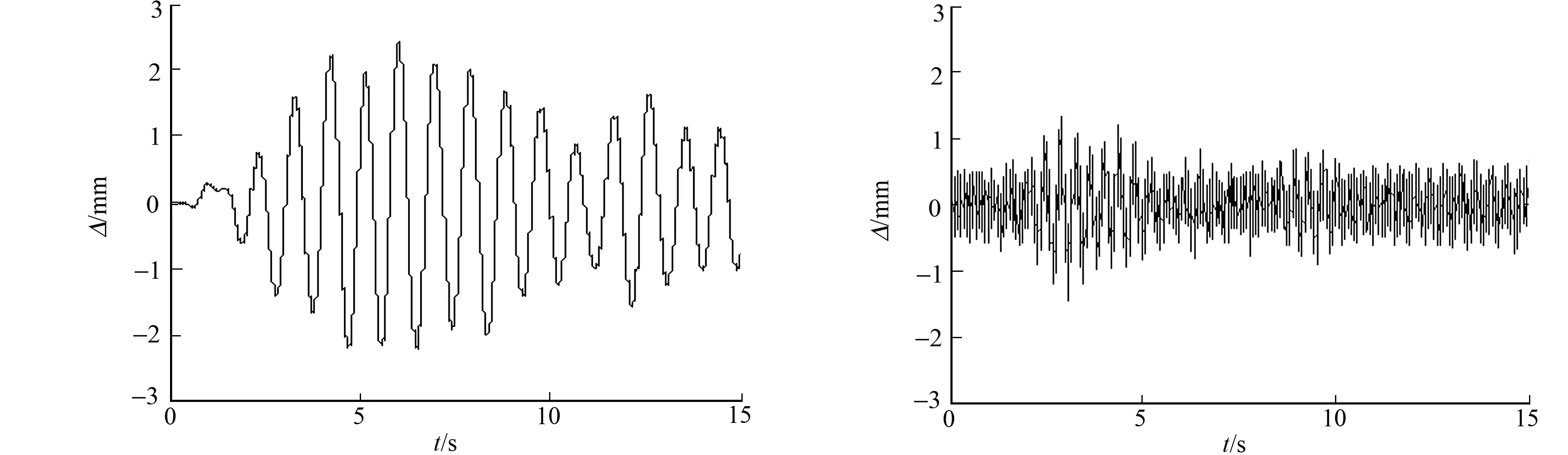
(a) 一阶IMF (b) 余量信号图3 DS2工况下AMD定理提取的分量信号Fig.3 Component signals extracted by AMD theorem under DS2 cases

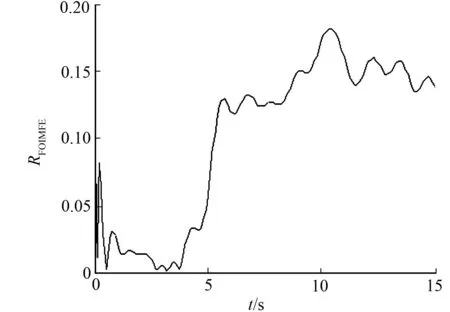
图4 DS2工况损伤识别结果Fig.4 Detection results of damage under DS2 cases

在成功识别结构损伤位置的基础上，以DS2工况为例，采用复 Morlet小波对提取的一阶IMF信号进行连续小波变换，并根据式(6)对小波系数进行求和;然后,在求和后的小波系数曲线上设置一个滑动时间窗，选取时间窗长为100(0.1 s)，以窗内的小波能量平均值代表滑动窗中心点的小波能量.同理,可以求出DS1未损伤工况下结构第一层响应的一阶本征函数小波能量.至此，可求解一阶本征函数小波能量变化率(RFOIMFE)，如图4所示.由图4可知:RFOIMFE在t=5 s时的突然增加,与剪切型结构第一层刚度突然降低10%有关.15%水平的高斯白噪声和端点效应虽然对损伤识别结果有一定的影响，但是时变损伤指标RFOIMFE仍然能够有效探测到结构损伤的发生时间.

3.2刚度线性变化工况下的损伤识别

设定三层剪切型结构某层的刚度发生线性变化，具体损伤工况如表3所示.结构各层的位移(Δ)通过龙格-库塔法求解，其中,采样频率仍为1 000 Hz.为简单起见，只给出了DS5工况下三层剪切型结构第一层的位移响应，如图5所示.通过AMD定理提取DS5工况下三层剪切型结构第一层位移响应的一阶分量信号和余量信号，结果如图6所示.同理可得第二层和第三层位移响应的一阶分量信号和余量信号.在成功提取各层一阶IMF分量信号的基础上，根据式(7)，(8)求解一阶本征函数能量比rj，如表3所示.

由表3可知：相比DS1工况即结构完好无损时，DS5工况中第一层位移响应的一阶本征函数能量比值r1增加，由此可知剪切型结构的第一层发生了软化现象，吸收了更多的能量，故而一阶本征函数能量比值相对增加.同理，在DS6和DS7工况中，根据一阶本征函数能量比指标值的变化，可以判断出结构相应的损伤位置分别为结构第二层和第三层，这与设定的损伤情况是完全吻合的.因此，一阶本征函数能量比指标完全可以准确识别刚度线性变化工况下结构的损伤位置.

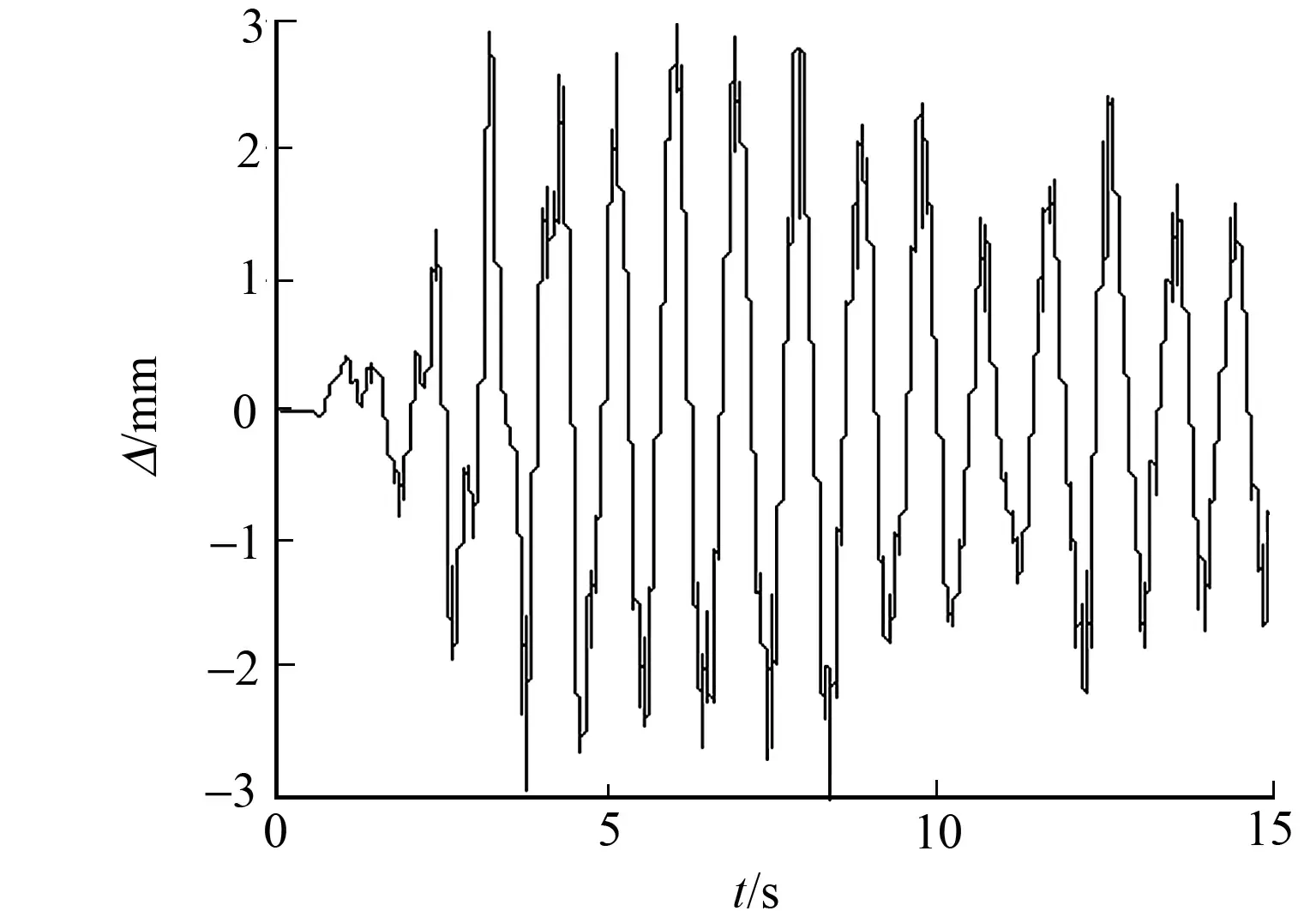
图5 DS5工况下结构第一层位移响应 Fig.5 Displacement responses of first story under DS5 cases

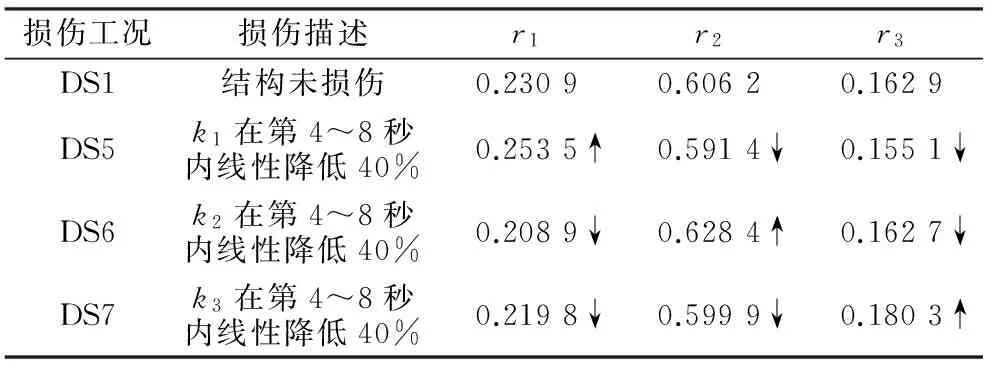
损伤工况损伤描述r1r2r3DS1结构未损伤0.23090.60620.1629DS5k1在第4～8秒内线性降低40%0.2535↑0.5914↓0.1551↓DS6k2在第4～8秒内线性降低40%0.2089↓0.6284↑0.1627↓DS7k3在第4～8秒内线性降低40%0.2198↓0.5999↓0.1803↑

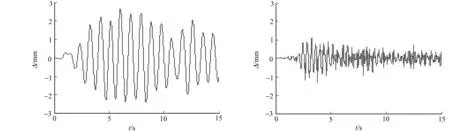
(a) 一阶IMF (b) 余量信号图6 DS5工况下AMD定理提取的分量信号Fig.6 Component signals extracted by AMD theorem under DS5 cases

以DS5工况为例，在成功识别结构损伤位置的基础上，可采用复 Morlet小波对提取的第一层位移响应的一阶IMF分量信号进行连续小波变换，并根据式(6)对小波系数进行求和;然后,在求和后的小波系数曲线上设置一个滑动时间窗，选取时间窗长为100(0.1 s)，以窗内的小波能量平均值代表滑动窗中心点的小波能量.同理,可求出DS1未损伤工况下结构第一层位移响应的一阶本征函数小波能量,并求解RFOIMFE，如图7所示.

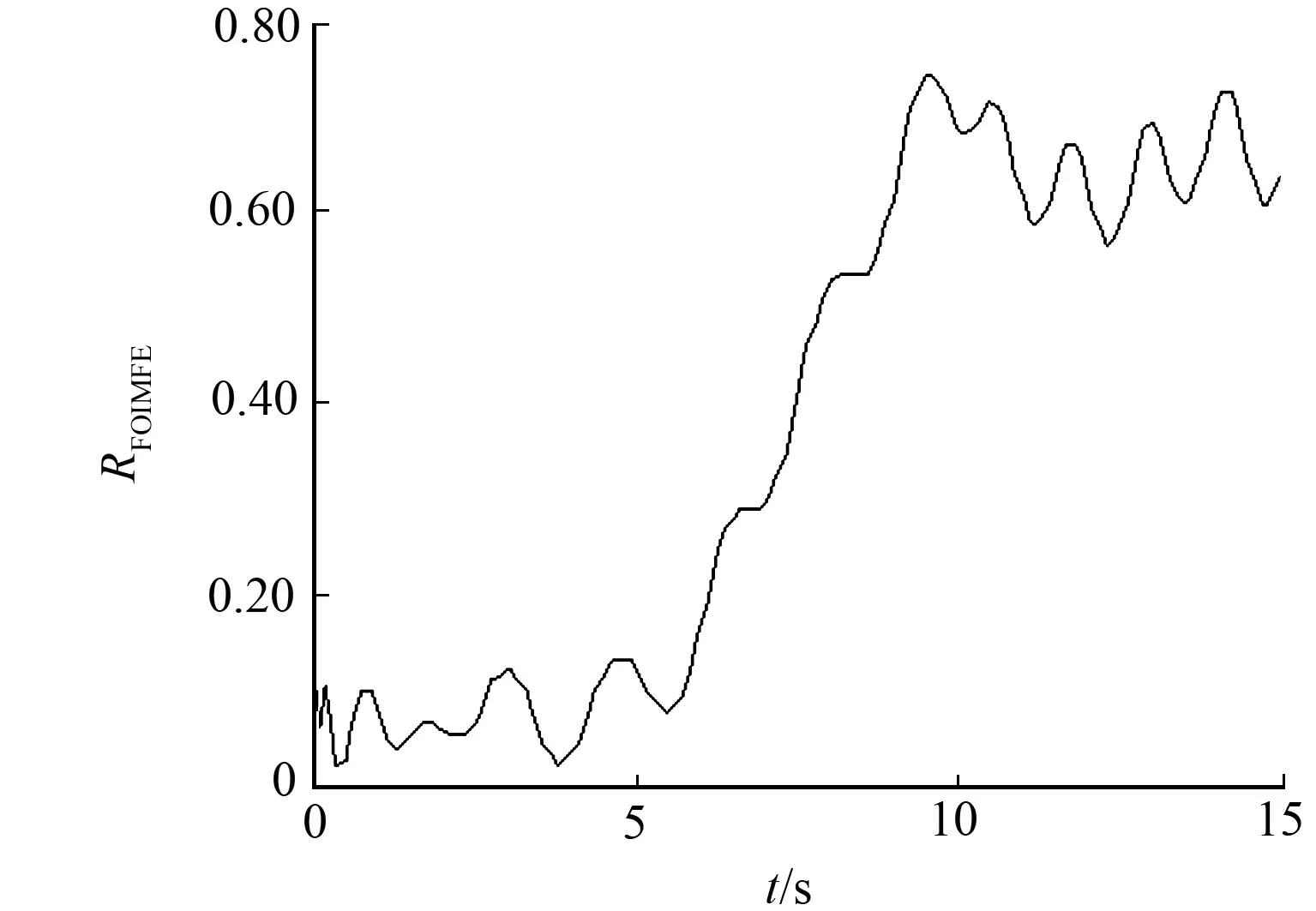
图7 DS5工况损伤识别结果Fig.7 Detection results of damage under DS5 cases

由图7可知：时变损伤指标RFOIMFE在t=4～8 s时间范围内的线性增加，与剪切型结构第一层刚度在时间4～8 s范围内线性降低40%有关.但是在第4秒附近，该指标的损伤识别效果并不是很好.这主要是因为以第4秒为中心点窗长包含了3.95～4.00 s和4.00～4.05 s这两个时间段，前一个时间段结构尚未发生损伤，而后一时间段结构发生了损伤，因此,损伤识别结果受到影响.此外，由于15%水平高斯白噪声的随机性，这个识别误差有可能在一定程度上被放大.但是总的来说，时变损伤指标RFOIMFE能够有效识别结构的损伤演化趋势.

4 结论

为解决HHT变换中存在的模态混叠问题，构建一阶本征函数能量比和一阶本征函数小波能量变化率两个损伤指标，并分别对结构的损伤位置和损伤时间进行识别.通过一个三层剪切型结构数值算例验证了损伤指标的有效性，得到以下2点主要结论.

1) 相比结构完好无损时结构某层一阶本征函数能量比值的增加，表明该层出现损伤，从而发生软化现象，吸收了更多的能量，同时也验证了一阶本征函数能量比指标识别损伤位置的准确性.

2) 在成功识别损伤位置的基础上，对损伤位置处的一阶IMF分量进行连续小波变换，并引入滑动时间窗思想提出的时变损伤指标RFOIMFE，其能够有效识别刚度突变和线性变化两种工况下结构的损伤发生时间.

[1] 王术新，姜哲.基于结构振动损伤识别技术的研究现状及进展[J].振动与冲击，2004，23(4):99-102.DOI:10.3969/j.issn.1000-3835.2004.04.024.

[2] CHIKKERUR S,CARTWRIGHT A N,GOVINDARAJU V.Fingerprint image enhancement using STFT analysis[J].Pattern Recognition，2007，40(1):198-211.DOI:10.1016/j.patcog.2006.05.036.

[3] 王忠仁，林君，李文伟.基于Wigner-Ville分布的复杂时变信号的时频分析[J].电子学报，2005，33(12):2239-2241.DOI:10.3321/j.issn:0372-2112.2005.12.032.

[4] 李秀坤，吴玉双.多分量线性调频信号的Wigner-Ville分布交叉项去除[J].电子学报，2017，45(2):315-320.DOI:10.3969/j.issn.0372-2112.2017.02.008.

[5] HUANG N E，SHEN Z，LONG S R，etal.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[M]∥The Royal Society.Proceedings of the Royal Society of London Series A: Mathematical， Physical and Engineering Sciences.London:The Royal Society，1998:903-995.

[6] HUANG N E，SHEN Z，LONG S R.A new view of nonlinear water waves: The Hilbert spectrum[J].Annual Review of Fluid Mechanics，1999，31:417-457.DOI:10.1146/annurev.fluid.31.1.417.

[7] WU Z H，HUANG N E.Ensemble empirical mode decomposition: A noise assisted data analysis method[J].Advances in Adaptive Data Analysis，2009，1(1):1-41.DOI:10.1142/S1793536909000047.

[8] 刘景良，任伟新，王佐才，等.基于同步挤压小波变换的结构瞬时频率识别[J].振动与冲击，2013，32(18):37-42.DOI:10.3969/j.issn.1000-3835.2013.18.007.

[9] CHEN Genda，WANG Zuocai.A signal decomposition theorem with Hilbert transform and its application to narrowband time series with closely spaced frequency components[J].Mechanical Systems and Signal Processing，2012，28(2):258-279.DOI:10.1016/j.ymssp.2011.02.002.

[10] WANG Zuocai，REN Weixin，LIU Jingliang.A synchrosqueenzed wavelet transform enhanced by extended analytical mode decomposition method for dynamic signal reconstruction[J].Journal of Sound and Vibration，2013,332(22):6016-6028.DOI:10.1016/j.jsv.2013.04.026.

[11] 王佐才，任伟新.基于解析模式分解的密集工作模态参数识别[J].噪声与振动控制，2013，33(6):18-24.DOI:10.3969/j.issn.1006-1335.2013.06.005.

[12] 韩建刚，任伟新，孙增寿.基于小波包变换的梁体损伤识别[J].振动、测试与诊断，2006，26(1):5-10.DOI:10.3969/j.issn.1004-6801.2006.01.002.

[13] 韩建刚，任伟新，孙增寿.结构损伤识别的小波包分析试验研究[J].振动与冲击，2006，25(1):47-50.DOI:10.3969/j.issn.1000-3835.2006.01.011.

[14] SOYOZ S，FENG M Q.Instantaneous damage detection of bridge structures and experimental verification[J].Structural Control and Heath Monitoring，2008，15(7):958-973.DOI:10.1002/stc.229.

[15] 熊飞，程远胜，刘均.基于HHT方法的时变多自由度系统的损伤识别[J].振动、测试与诊断，2008，28(2):122-125.DOI:10.3969/j.issn.1004-6801.2008.02.009.

[16] 刘景良，任伟新，王佐才.基于同步挤压和时间窗的时变结构损伤识别[J].振动与冲击，2014，27(6):835-841.DOI:10.3969/j.issn.1004-4523.2014.06.005.

[17] 任宜春，翁璞.基于改进Hilbert-Huang变换的结构损伤识别方法研究[J].振动与冲击，2015，34(18):195-199.DOI:10.13465/j.cnki.jvs.2015.18.033.

(责任编辑： 黄仲一英文审校： 方德平)

StructuralDamageDetectionUsingAnalyticalModeDecompositionandWaveletTransform

LIU Jingliang1， GAO Yuan1， LUO Yongpeng1， ZHENG Wengting2

(1. School of Transportation and Civil Engineering， Fujian Agriculture and Forestry University， Fuzhou 350002， China；2. School of Civil Engineering， Fujian University of Technology， Fuzhou 350118， China)

10.11830/ISSN.1000-5013.201705022

2017-05-13

刘景良(1983-)，男，讲师，博士，主要从事桥梁结构健康监测的研究.E-mail:liujingliang@fafu.edu.cn.

国家自然科学青年基金资助项目(51608122)； 福建省青年科技人才创新项目(2016J05111)； 福建农林大学青年教师科研基金资助项目(113-61201405104)

TU 311.3

A

1000-5013(2017)05-0643-06