激励频率对扭转模态磁致伸缩导波检测性能影响

李志农， 孟宁， 龙盛蓉

(南昌航空大学 无损检测技术教育部重点实验室， 江西 南昌 330063)

激励频率对扭转模态磁致伸缩导波检测性能影响

李志农， 孟宁， 龙盛蓉

(南昌航空大学 无损检测技术教育部重点实验室， 江西 南昌 330063)

在综合考虑力-磁-声的多个物理场耦合的基础上，通过采用有限元数值仿真方法模拟扭转模态磁致伸缩导波对铁磁性管道的检测，研究激励电流频率对T模态导波检测效果的影响，并通过实验给予验证.结果表明：实验研究数据与仿真计算结果具有相同的变化趋势且存在一个最优频率；激励频率对检测效果有着明显的影响，通过调整激励频率能够使扭转模态导波幅值最大，实现磁致伸缩导波检测性能的优化.

超声导波； 扭转模态； 磁致伸缩效应； 激励频率； 导波检测； 有限元仿真

Abstract： On the basis of considering the coupling of stress-magneto-acoustic multiple physical fields， the finite element numerical simulation method was used to simulate the torsional mode of magnetostrictive guided wave on the detection of ferromagnetic pipe. The effect of excitation current frequency on the guided wave detection of T mode was studied. The experiment results show that the numerical simulation and experiment test have very good consistency. The excitation frequency has a significant effect on the detection effect， and the amplitude of the torsional mode guided wave can be maximized by adjusting the excitation frequency, which can realize the optimization of the performance of the magnetostrictive guided wave detection.

Keywords： ultrasonic guided wave; torsional mode; magnetostrictive effect; excitation frequency; guided wave detection; finite element simulation

超声导波检测技术具有速度快、检测距离长，以及能一次性完成对整个工件检测等优势，广泛应用于管道检测中.管道中导波的传播方式主要有纵向模态L(n，m)、扭转模态T(n，m)、弯曲模态F(n，m)[1].纵向模态传播速度快、激发方式简单，通常用于管道的周向裂纹的检测中，然而，该模态导波对纵向裂纹并不够敏感.与纵向模态相比，扭转模态的传播特性具有非频散特点，且在传播过程中能量衰减较小，不受管道中液体的影响[2].在现有研究中，对纵向模态的理论研究、仿真和实验分析较多.龙盛蓉[3]对纵向磁致伸缩导波传感器进行了有限元模拟仿真，对其可能的影响因素做了细致研究，并加以实验验证.Ludwig等[4]开发了包括磁致伸缩的超声导波有限元模型，但没有针对实验进行验证，也没有包括从实际测量导出的物理参数.在扭转模态方面，何存富等[5-6]基于压电式传感器对扭转模态导波管道缺陷检测进行仿真模拟，并对充水管道缺陷进行实验研究.Kwun等[7]和Kim等[8]研制了基于磁致伸缩效应的磁致伸缩传感器，实现在单层钢管中激励出T(0，1)模态并进行了缺陷检测.本文在前人研究基础上，运用有限元仿真方法对管道中扭转模态导波的激励情况进行数值模拟，并结合仿真模拟和实验结果数据，分析激励电流频率对扭转导波回波信号的影响.

1 扭转模态磁致伸缩导波检测原理

1.1磁致伸缩导波激励传感器检测原理

导波的激励过程是将电磁能转变为弹性能，其中，弹性波是由激励线圈产生的交变磁场在管道中激发出的.若在线圈中施加的激励电流密度为J0，则产生的动态磁场本构方程[9]可以表示为

2A-μσ=-μ(Js+J0).

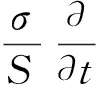
本构方程的动态组件可以由线性项近似表示，应变和磁场[10-11]可以表示为

式(2)中：SH为6×6的弹性矩阵；μσ为3×3的磁导率矩阵；σ为应力；SHσ为管道中应力所产生的应变；dHd为磁致伸缩效应所产生的外加应变.d为rθz坐标系下6×3的磁致伸缩系数矩阵，可表示为

1.2扭转模态导波激励传感器结构

(a) 动态磁场结构 (b) 静态磁场结构图1 扭转模态磁致伸缩导波传感器结构Fig.1 Sensor structure of torsional mode magnetostrictive guided wave

扭转模态磁致伸缩导波激励传感器结构，如图1所示.用通电流的螺线圈绕管壁缠绕来产生动态激励磁场，如图1(a)所示;而对贴于管道外侧的矩形镍片沿长度方向进行磁化，使其处在偏置静态磁场的周向磁化状态下，如图1(b)所示.依据Wiedemann效应，待检测工件中材料介质质点受到由激励线圈产生的沿管道轴向的磁致伸缩力，以及由偏置静态磁场产生的沿管道周向的磁致伸缩力的共同影响，即可形成扭转模态的磁致伸缩导波[3].

2 有限元模型仿真及结果分析

2.1仿真模型建立

对铁磁性管道的数值模拟仿真是通过有限元软件COMSOL Multiphysics实现的，几何模型主要有交变线圈、钢管、镍带和空气等4个部分.整个管道扭转模态磁致伸缩导波激励模型的建立过程，包括模型各部分尺寸大小的选择、添加材料属性、边界条件的定义，以及设置计算时间和网格划分.这些因素的选取和设定对仿真计算结果的准确性和计算效率都有非常大的影响.因此，在保证计算精度和完整性的基础上，将管道仿真模型的长度设置为100 mm，外径为48 mm，壁厚为4 mm，激励线圈匝数为40匝，激发导波的频率选择为120 kHz.管道材料属性为铁磁性，如表1所示.表1中：E为杨氏模量；υ为泊松比；ρ为密度；σ为电导率；λs为饱和磁致伸缩量；Ms为饱和磁化强度.

表1 磁致伸缩材料特性Tab.1 Magnetostrictive material characteristics

模型所加载的激励信号选用汉宁窗调制的6个周期正弦信号，有

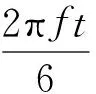
式(4)中：I为电流大小；f为激励频率.

图2 仿真模型网格划分Fig.2 Mesh devision of simulation model

COMSOL Multiphysics是以有限元法为基础的多物理场仿真软件，主要用于解决多个物理场耦合作用下的仿真模拟问题.管道磁致伸缩扭转模态导波激励模型是利用COMSOL Multiphysics中电磁学模块及固体力学两部分进行耦合分析.在电磁学分析部分，建立管道三维模型并划分网格，计算激励端镍带产生的静态偏置磁场的值，同时利用式(1)建立动态磁场模型.在建立的动态磁场模型上，由式(2)求解激励磁场引起的磁致伸缩应变，并把该应变作为输入，加载到激励线圈下方的管道区域，计算在该机理下产生的位移场[9].网格划分后的模型,如图2所示.

2.2仿真求解分析

通过仿真求解计算，分析在管道中激励缠绕线圈产生的动态磁场的方向.取有限元管道模型中靠近线圈的任一质点为研究对象，该质点在交变磁场下的磁通密度(T)的一维图像,如图3所示.根据右手定则可以判定，绕管壁激励线圈产生的磁场应沿x轴方向分布.由图3可知：在沿管道轴向x轴方向通过质点的磁通密度最大，而沿y轴方向和z轴方向几乎为0，符合磁场产生规律.因此，由线圈激励出的动态磁场是沿管道轴向分布的.

管壁中由激励线圈和周向磁化镍带产生的合成磁场的方向，如图4所示.因为由镍带形成的周向偏置磁场远大于线圈产生的交变轴向磁场，并且由于镍带处于线圈与管壁的中间位置(图2)阻碍了交变磁场对管壁的磁化，所以最终动态磁场和静态磁场的耦合作用只对管壁形成周向磁化.

图3 交变磁场质点磁通密度 图4 耦合磁化条件下磁场分布图Fig.3 Particle magnetic flux density in alternating magnetic field Fig.4 Magnetic field distribution under coupled magnetization

其次,为了研究管道中质点振动位移情况，在模型中镍带正下方管壁中心，约距离管道表面2 mm处取点(100，0，24)，仿真计算该点处管壁自身的磁致伸缩位移(Δ)，其结果如图5，6所示.

由图5,6可知：管壁中质点振动位移的周向分量(Δy)值为1.5×10-14mm，其数值比轴向位移分量(Δx)高出一个数量级.因此,可以确定该激励模型产生的导波符合铁磁性材料扭转模态导波的传播特性，即以周向振动为主，产生的波沿管道轴向传播，传播方向与质点振动方向相垂直.这说明通过该仿真分析能够得到由力磁声多场耦合产生的应变，能够真实反映扭转模态磁致伸缩导波.

图5 质点周向位移与时间的关系 图6 质点轴向位移与时间的关系Fig.5 Relationship between circumferential displacement of particle and time Fig.6 Relationship between axial displacement of particle and time

图7 激励电流频率对质点振动位移的影响Fig.7 Influence of exciting current frequency on vibration displacement of particle

3 激励电流频率的影响

3.1数值计算分析

在上述建立的激励仿真模型的基础上，给交变线圈分别加载 60～160 kHz 不同频率的电流，仿真计算分析交变线圈中激励电流频率对T模态导波检测信号的影响.当激励线圈电流频率为 60～160 kHz 时，分别计算管道(100，0，24)处质点的磁致伸缩振动位移分量(Δy)，如图7所示.

由图7可知：当激励频率小于120 kHz时，随着激励电流频率的增大，磁致伸缩振动周期与幅值均增大；当激励频率为120 kHz时，扭转导波磁致伸缩振动幅值达到最大；但当交流线圈激励电流频率超过120 kHz时，随着频率的增大，质点的磁致伸缩振幅逐渐减小.说明激励频率对导波激励信号强度有影响，存在一个最优激励频率,使产生的导波信号最好.

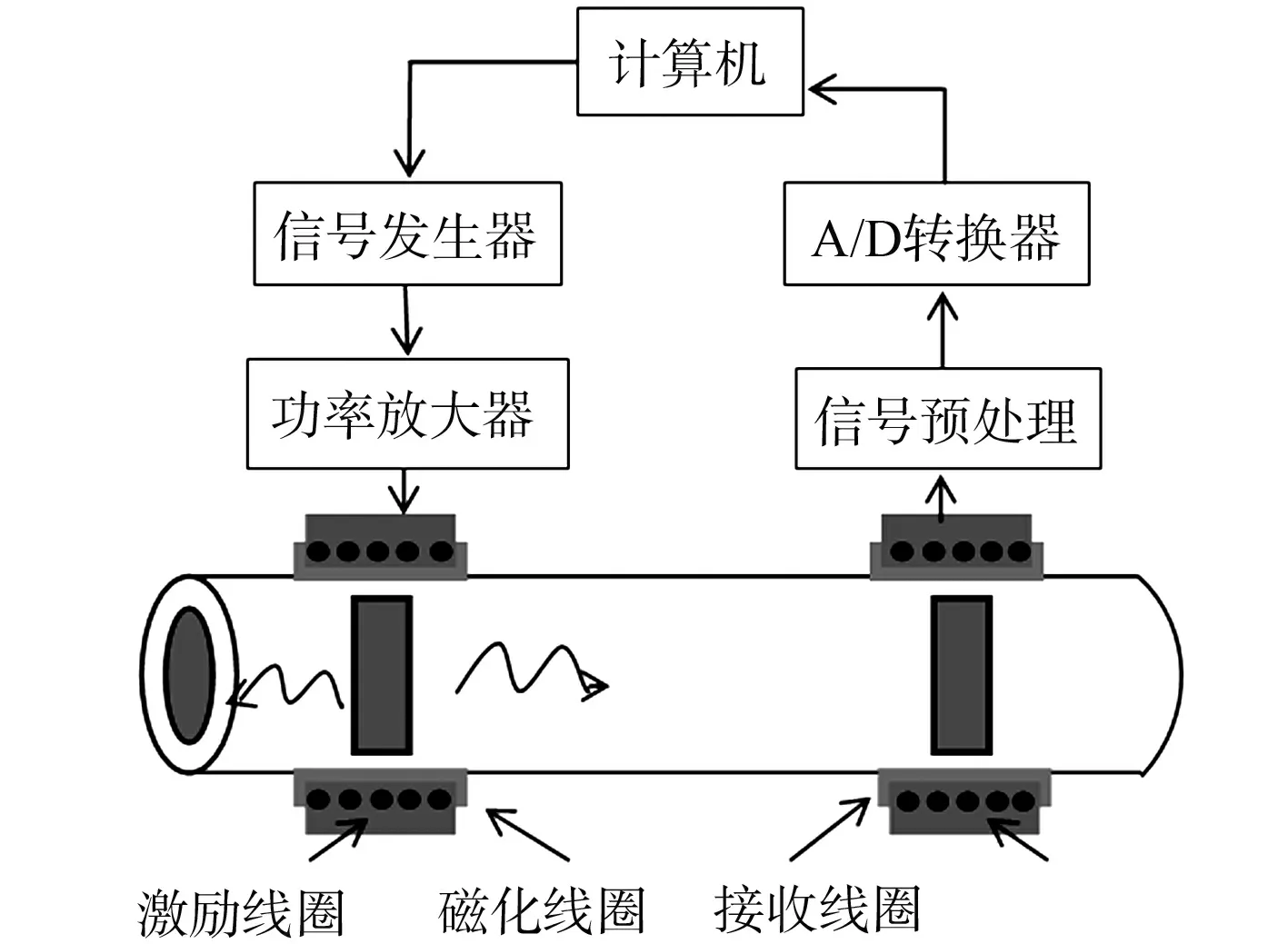
图8 磁致伸缩扭转导波实验装置示意图Fig.8 Experiment equipment diagram of torsional magnetostrictive guided wave

3.2实验验证

为了验证上述仿真分析的正确性，搭建管道磁致伸缩扭转导波检测实验平台，如图8所示.磁致伸缩扭转导波传感器的激励装置放置在距离管端的550 mm处，接收装置放置在距离管道同一端的1 180 mm处.通过信号发生器给予的激励信号经过功率放大器后，输入激励线圈进行扭转导波的激励，产生的导波经过接收装置产生相应感应的电压信号，最后输出到计算机上显示.实验使用的磁致伸缩导波传感器参数：镍带尺寸为150.0 mm×30.0 mm×0.2 mm；激励线圈匝数为40匝；激励线圈漆饱线直径为0.52 mm；接收线圈匝数为200匝；接收线圈漆饱线的直径为0.21 mm；管道长度、内径、外径分别为3 200，44，48 mm.除管道长度外，磁化镍带和动态激励线圈的尺寸参数与仿真模型一致.

给线圈施加6个周期的激励信号，保持激励电流强度为10 A，分别给交变线圈加载频率为60，80，100，120，140，160 kHz 的激励电流，采集得到的导波检测回波信号,如图9所示.图9(a)中：A为幅值；加载频率为60 kHz得到的波形，标注的回波1为空间干扰波，2为首次到达波，3，4，5均为端部反射波.

根据首次到达波和端部反射波3进行导波波速计算，从图9中读出首次到达波时刻为273 μs，端部回波信号3位于为613 μs处，则计算得到波速为3 235 m·s-1.与理论扭转导波波速3 200 m·s-1的相对误差很小，可知激励得到的导波为扭转模态导波.

(a) f=60 kHz (b) f=80 kHz

(c) f=100 kHz (d) f=120 kHz

(e) f=140 kHz (f) f=160 kHz图9 不同激励频率下磁致伸缩扭转导波Fig.9 Torsional magnetostrictive guided wave under different excitation frequency

由于在实验中不能通过质点振动位移的方法进行研究，所以采用对回波信号峰值的分析方法确定电流激励频率对导波强度的影响，从而确定合适的检测频率.实验中选取了回波信号中首次界面回波，并以其峰值Vp-p作为判断标准，如图9(a)中标注所示.

分别提取仿真结果中不同激励频率下磁致伸缩振动幅值的最大值点(Δmax)，与实验结果中不同激励频率下回波信号的峰值(U)，绘制的关系图如图10所示.

由图10(b)可知：不同的激励频率产生的回波信号峰值是不同的，在f=120 kHz时，扭转导波的回

(a) 仿真导波振动幅值的最大值 (b) 实验导波峰值图10 不同频率下实验结果与仿真结果对比图Fig.10 Comparison chart of experimental results and simulation results

波信号峰值达到最大，此结论与仿真计算结果(图10(a))中的变化规律相一致.由此可见，在保持激励电流大小一定的情况下，选择不同的信号激励频率对于磁致伸缩传感器的性能是有影响的，且存在一个最优激励频率使导波检测信号最好.

4 结论

根据磁致伸缩导波传感器检测方程，在研究扭转模态磁致伸缩导波激励传感器结构的基础上，采用有限元软件建立了管道磁致伸缩扭转模态导波激励过程的检测仿真模型，并根据分析质点振动情况验证了该激励模型激发出的导波符合扭转模态导波的特性.

另外，通过仿真模拟和实验研究在不同激励电流频率下对T模态导波强度的影响情况，说明激励频率对导波激励信号强度有影响，存在一个最优激励频率使扭转模态导波幅值最大，检测效果较好.该模型结合仿真和实验对扭转导波的激励过程进行综合分析，可为磁致伸缩扭转导波传感器的设计研究提供帮助.

[1] ROSE J L.Ultrasonic waves in solid media[M].Cambridge:Cambridge University Press，1999:154-163.

[2] KIM Y G，MOON H S，PARK K J，etal.Generating and detecting torsional guided waves using magnetostrictive sensors of crossed coils[J]．Ndt and E International,2011,44(2):145-151.

[3] 龙盛蓉.铁磁性管道磁致伸缩导波检测机理及传播特性研究[D].南昌:南昌大学,2014:33-34.

[4] LUDWIG R，DAI X W.Numerical simulation of electromagnetic acoustic transducer in the time domain[J].J Appl Phys，1991，69(1):89-98.

[5] 何存富，李伟，吴斌.扭转模态导波检测管道纵向缺陷的数值模拟[J].北京工业大学学报，2007，33(10):1009-1013.

[6] 刘增华，吴斌，何存富，等.扭转模态在充水管道缺陷检测的实验研究[J].仪器仪表学报，2006，27(6):1587-1589.

[7] KWUN H，KIM S Y，LIGHT G M.Long-range guide dwave inspection of structures using the magnetostrictive sensor[J].Journal of the Korean Society for Nondestructive Testing，2001，21(4):383-390.

[8] KIM Y Y，PARK C，CHO S H，etal.Torsional wave experiments with a new magnetostrictive transducer configuration[J].Journal of the Acoustical Society of America，2005，117(4):3459-3468.

[9] 孙鹏飞，武新军，从明.磁致伸缩纵向导波管道检测数值建模与分析[J].仪器仪表学报,2015,36(6):1251-1255.

[10] RIBICHINI R,CEGLA F,NAGY P B,etal.Quantitative modeling of the transduction of electromagnetic acoustic transducers operating on ferromagnetic media[J].IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2010,57(12):2808-2817.

[11] 王亚午.电磁超声换能器多场耦合分析及实验研究[D].武汉:湖北工业大学,2015:41-47.

(责任编辑： 黄仲一英文审校： 崔长彩)

InfluenceofExcitationFrequencyonDetectionPerformanceofTorsionalModeMagnetostrictiveGuidedWave

LI Zhinong， MENG Ning， LONG Shengrong

(Key Laboratory of Nondestructive Testing of Ministry of Education, Nanchang Hangkong University， Nanchang 330063)

10.11830/ISSN.1000-5013.201610030

2016-10-24

李志农(1966-)，男，教授，博士，主要从事智能检测方面的研究.E-mail:lizhinong@tsinghua.org.cn.

国家重点研发计划项目(2016YFF0203000)； 国家自然科学基金资助项目(51261024， 51675258)； 江西省教育厅科学技术研究项目(GJJ150699)； 南昌航空大学无损检测技术教育部重点实验室开放基金资助项目(ZD201429003)； 南昌航空大学博士科研启动项目(EA201508008)

TB 512

A

1000-5013(2017)05-0632-06