对中证500指数波动性的分析研究——基于A RM A-G A RCH族模型

涂犁明，方 华

（上海理工大学管理学院，上海200093）

对中证500指数波动性的分析研究
——基于A RM A-G A RCH族模型

涂犁明，方 华

（上海理工大学管理学院，上海200093）

以中证500指数收益率为研究对象，利用不同假设分布的GARCH族模型对收益率波动性进行分析。结果表明：收益率序列存在明显的波动集群现象，而且并非正态分布；基于t分布下的ARMA(1，1)-GARCH(1，1)模型可以较好的描述收益率序列的波动集群现象；基于GED分布的ARMA(1，1)-EGARCH(1，1)模型则是最佳模型，同时说明了中证500指数收益率存在杠杆效应，且利空消息影响大于利好消息。

GARCH模型；EGARCH模型;AIC;t分布；GED分布

Abstract:This paper makes the return of the CSI 500 index as the research object and uses the GARCH model with different assumptions to analyze the volatility of returns.It shows obvious volatility clustering in return series,and it is not normal distribution.In this paper,the ARMA(1,1)-GARCH(1,1)model with t distribution can describe the volatility clustering of return series.The ARMA(1,1)-EGARCH(1,1)model based on the GED distribution is the best model,and shows that the return of the CSI 500 index exist leverage effect,and bad news always cause a large fluctuation than good news.

Key words:GARCH model;EGARCH model;AIC;t-distribution;GEDdistribution

1 引言

吴长凤[1]首次利用回归-GARCH模型初步研究了上证指数和深证指数波动性之间的关系。程千里，周少甫证明了我国股市收益存在尖峰厚尾特点，和波动集群，同时证明存在不对称性。陈健[2]则在GARCH模型中引入t分布代替正态分布假设进行上证指数的实证。马丹[3]对上证指数收益率进行多个GARCH模型的分析说明了我国股市杠杆效应存在。鲁万波[4]则运用了非参数GRACH(1，1)模型来进行研究，证明了在对我国股市的预测上，非参数模型更加精确。李杰和朱文俊[5]利用GARCH-M模型比较了上证指数和国外6个综合指数，说明了相对成熟市场，我国股市的波动比较剧烈，而对于新兴市场国家，我国股市的波动属于温和。茹正亮，杨芝艳[6]等评价了各种利非对称的GARCH模型对我国股市的预测能力。在直接对中证500指数的研究中，杜雨薇[7]利用GARCH模型和EGARCH模型对指数收益率进行建模，并进行了五个月的预测。

以上文献直接对中证500指数进行研究的文章较少，大多对上证指数，深证指数进行研究，很少有学者关注中证500指数，本文试图对这反映小市值公司股价的指数做一些初步研究。同时过往研究中均值模型和条件方差模型的选择也比较模糊，本文试图利用AIC信息准则解决这个问题。

2 实证模型简介

2.1 GARCH模型

GARCH模型也即是广义自回归条件异方差模型是由 Bollerslev（1986）在Engle提出的 ARCH模型基础上发展而成的，该模型能够较好地解决时间序列中由于波动而产生的异方差现象。而且使得待估参数减少，对未来条件方差的预测更加准确。GARCH(1,1)模型的具体形式为:

其中（1）式称为GARH模型中的均值方程，其中Xt*为解释变量向量，β为相应的系数向量。εt为扰动项，一般假设其服从标准正态分布，但金融数据往往存在尖峰厚尾现象，所以有时也使用t分布或者广义误差分布（GED分布）等；（2）式为GARCH模型中的条件方差方程，反映的是均值方程中残差项的波动情况。

2.2 TARCH模型

对资产价格波动性的影响“坏消息”往往总是大于“好消息”，针对此，Glosten，Jagannathan and Runkle（1993）提出了非对称的“门限 GARCH”模型，简记为GARCH模型，以TARCH(1,1)模型为例，均值方程不变，该模型中的条件方差被设定为：

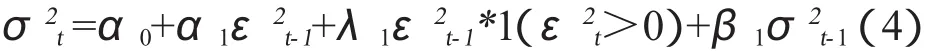
其中，1(·)是一个示性函数，即当均值方程中的εt＞0时，其值为1，反之，其值为0。λ1ε2t-1*1（εt-1＞0）即为非对称效应项，只要λ1显著不为零，则存在非对称效应。否则不存在。

2.3 EGARCH模型

同样，EGARCH模型也是针对非对称效应而推广的，它是由Nelson（1991）提出的，同时在标准的GARCH模型中，对参数的取值有所限制，使MLE估计不便，EGARCH模型对参数没有要求，从而更适合建模以一个EGARCH(1,1)模型为例，该模型相对于GARCH(1,1)模型均值方程不变，方差方程做了一定的改动，即

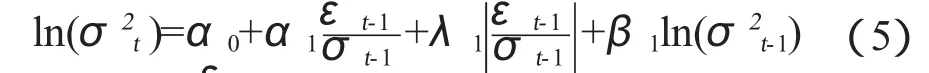
3 实证分析

文章选取了中证500指数从2010年1月4日到2017年4月28日共1 777个交易日数据，数据来源于东方财富网。为得到收益率数据，通过对中证500收盘价进行对数差分，即：

从而得到1 776个对数收益率数据，本文利用软件stata11[8]和eviews8进行数据处理和模型建立。

3.1 统计性描述

由图1可知，收益率序列围绕0值上下波动，没有明显的趋势变化，但却存在明显的波动性聚集现象，也即是方差大的观测值聚集到一起，方差小的观测值聚集到一起。初步判定中证500指数可能适合运用GARCH族模型。

?

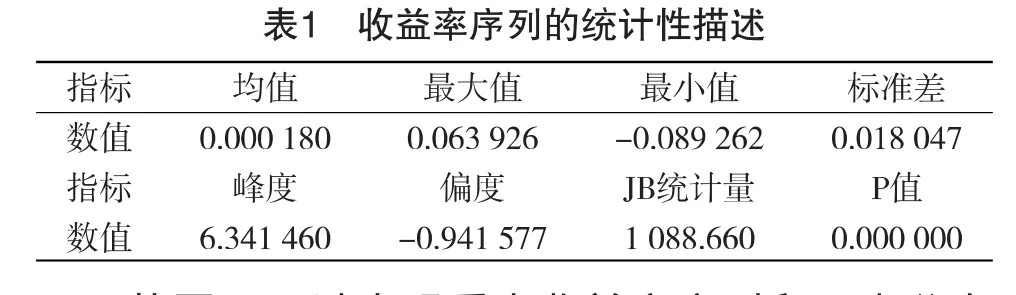
从图2可以直观看出收益率序列和正态分布存在很大差别，从表一的峰度 6.341 460＞3,偏度-0.941 577＜0可以更准确的说明收益率序列存在尖峰厚尾现象，而且左尾较厚。从JB统计量和P值则明确拒绝了收益率序列服从正态分布的假设。为了建模的准确，可以使用t分布和GED分布等来描述尖峰厚尾。

3.2 平稳性检验

?

为了模型的有效，对时间序列数据在建模前必须检验其平稳性，本文采用广泛使用的ADF单位根检验来检验中证500指数收益率序列的平稳性。从上表的结果可得，无论是在10%，5%还是1%置信水平上ADF值都小于相应的临界值，从而拒绝了存在单位根的原假设，也即是收益率序列是平稳的。

3.3 均值方程的选择

r序列的自相关系数和偏相关系数滞后一阶显著不为零，其他不显著，但也存在高阶滞后系数显著不为零的情况，由于文章篇幅，相关系数图不给出。考虑到建模的可操作性，本文在常用的几种模型中根据信息准则选择最优的ARMA模型，也即是garch模型中的均值方程。

其 中 ，arma10、arma11、arma12、arma20、arma21和 arma22 分别表示模型 AR(1)、ARMA(1，1)、ARMA(1，2)、AR(2)，ARMA(2，1)和 ARMA(2，2)。L.ar和 L2.ar分别是滞后一阶和滞后二阶收益率前估计系数，L.ma和L2.ma则为对应滞后一阶和二阶残差项前估计系数。

由图3可得，无论是考虑到信息准则AIC还是估计系数的显著性，ARMA(1，1)模型都是最优，虽然AR(1)的 BIC 小于 ARMA(1,1)，但显然 ARMA(1，1)模型对收益率序列拟合更加充分，综上所述，均值方程选择ARMA(1，1)，具体方程如下：

3.4 ARCH模型选择

均值方程选择好之后，可以通过均值方程的残差检验是否存在ARCH效应，本文通过对残差的平方进行Q检验（由于篇幅有限，Q检验结果不给出），发现残差平方存在高阶的相关性，证明残差存在明显的ARCH效应，需要建立ARCH模型。根据已有研究表明，对于金融时间序列的ARCH效应，GARCH（1,1）模型便可以很好的描述。所以本文同样选择GARCH(1，1)模型。考虑到对于股票指数数据可能存在非对称性效应，因此也试图建立相应的TARCH模型和EGARCH模型。同时由上文的正态性检验可知，收益率序列存在尖峰厚尾现象，因此考虑用t分布假设和GED分布假设而非正态分布假设。尽管多数论文依然将正态假设给出作为比较模型，但设定本身就不正确，没有什么参考价值，因此本文不再考虑此假设。

其中，L.tarch是TARCH模型非对称项前估计系数，L.earch_a是EGARCH模型非对称项前估计系数。

由图4的结果，可以剔除两个TARCH模型，因为TARCH项的估计系数不显著，说明不存在非对称效应。从AIC信息准则来看EGARCH(1，1)-GED模型最优，而且EGARCH项前系数显著不为零说明了非对称效应是存在的。其次较好的模型是GARCH(1,1)-t，这个模型没有考虑非对称效应是否存在。

最终 ARMA(1，1)-GARCH(1，1)-t模型方程为：

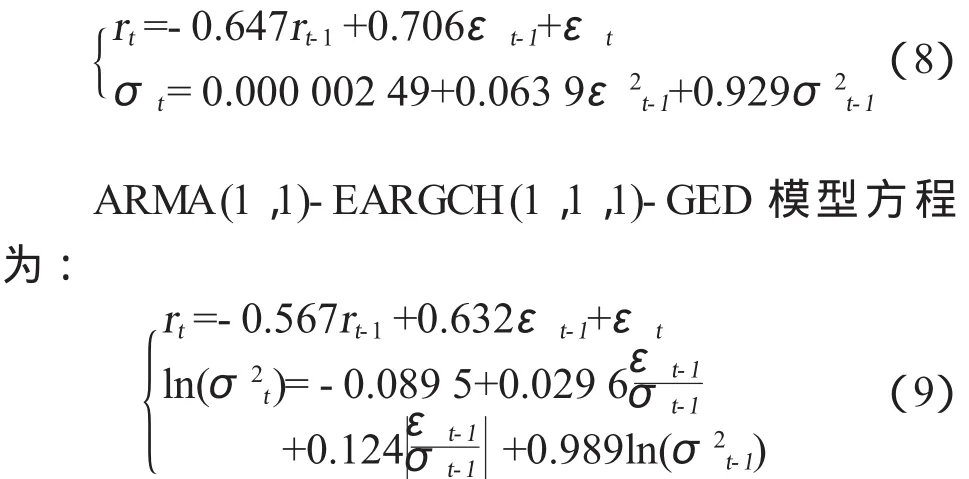
3.4 实证结果分析

分别对以上两模型的残差进行ARCH-LM检验，发现残差已经不存在ARCH效应，这说明上述两模型已经很好的解决了收益率序列的ARCH效应。从以上实证结果可以得出，基于不同分布假设的分析是非常有必要的的，因为不同的假设所得模型的估计是不一样的，也会影响估计的显著性。从以上两模型的均值方程来看，本时期的收益率与上一时期呈负相关关系，而与上时期的波动呈正相关关系，而且正向关系大于负向相关系。从条件方差模型来看，在 ARMA(1，1)-EARGCH(1，1，1)-GED模型方程中，反映“非对称”效应的系数为 -0.029 6＜0,说明了“非对称”效应存在，而且当时，对条件方差的对数的作用是0.124-0.029 6=0.094 4倍，当是对条件方差的对数的作用为 0.124- （-0.029 6）=0.153 6倍。这说明负作用对波动性的影响大于了正作用对波动性的影响，也即是股市中所谓的“利空消息”的对股价的影响大于“利好消息”（杠杆效应）。

4 结论

在对中证500指数收益率的统计性分析中可得，收益率存在尖峰厚尾现象，正态假设在此不合适，这和上证指数和沪深300等指数有着一样的结论，同时从收益率的时序图也可以看到，收益率存在波动集群现象，和大盘指数也一样。也即是从一般统计角度看，反映小市值公司的股价指数与反映大指数公司的股价指数形态大致一样。说明我国股市指数变动存在一致性。

在众多模型中，ARMA(1，1)-EGARCH(1，1)-GED是选择的最优的模型，而 ARMA(1，1)-GARCH(1，1)-t模型次优，但却忽略了可能存在的杠杆效应。还可以看出即使同样的模型，当残差的分布假设不同时，模型的拟合程度也不一样，这说明在模型的建立要考虑充分，不可遗漏。

最优的模型说明了中证500指数收益率存在杠杆效应，利空消息的影响是0.153 6倍，而利好消息的影响是0.094 4倍。这和我国股市现状是相吻合的，侧面说明模型建立是正确的。本文结论说明了为了我国股市的良好发展，对于投资者而言，要加强自身专业水平，不可人云亦云推波助澜。对于市场监督者来说必须预防虚假消息对投资者的诱导，只有这样我国股市才能逐渐走向成熟。

[1]吴长凤.利用回归-GARCH模型对我国沪深股市的分析[J].预测,1999(4):47-48.

[2]陈健.ARCH类模型研究及其在沪市A股中的应用[J].数理统计与管理,2003(3):10-13,26.

[3]马丹.上证指数收益率GARCH模型族分析[J].财经科学,2003(S1):33-36.

[4]鲁万波.基于非参数GARCH模型的中国股市波动性预测[J].数理统计与管理,2006(4):455-461.

[5]李杰,朱文俊.关于中国股市波动“剧烈”的实证分析[J].价格月刊,2010(1):87-91.

[6]茹正亮,杨芝艳,朱文刚,高安力.不同分布下非对称GARCH模型波动率预测评价[J].西南师范大学学报(自然科学版),2012(11):19-23.

[7]杜雨薇.对中证500的实证研究与趋势预测:基于GARCH模型和EGARCH模型[J].商,2016(18):200-201.

[8]陈强.高级计量经济学及Stata应用(第二版)[M].北京:高等教育出版社，2010.

［责任编辑：路 实］

A Study on Volatility of CSI 500 Index Based on ARMA——GARCH Model

TULi-ming，FANGHua
(College ofManagement，UniversityofShanghai for Science and Technology，Shanghai 200093，China)

F830.9

A

1673-5919（2017）04-0093-04

10.13691/j.cnki.cn23-1539/f.2017.04.032

2017-06-23

涂犁明（1993-），男，四川南充人，硕士研究生。