The Fuzzification of Attribute Information Granules and Its Formal Reasoning Model
Ruqi Zhou, Jiali Feng, Huiyou Chang, and Yuepeng Zhou
TheFuzzificationofAttributeInformationGranulesandItsFormalReasoningModel
Ruqi Zhou*, Jiali Feng, Huiyou Chang, and Yuepeng Zhou
The model of attribute information granule based on the method of attribute theory and the problem of fuzzification of attribute information granules are discussed. The concept of information granule given by Lotfi A. Zadeh can be explained with an attribute and its qualitative mapping operator. Finally, this paper also discusses the reasoning of granulation form of attribute fuzzification information which is based on the fuzzy Petri net, with the good formalization structure of fuzzy Petri net, as well as its asynchronous, concurrency, uncertainty and other characteristics which is similar to those of human cognitive activities, enabling the fuzzy Petri net to express the basic characteristics of a cognitive system in the form of computing attribute granules. The results of this paper can provide a reference for the establishment of the granular logic model in the uncertain problems and a new interpretation framework for revealing the inherent laws of knowledge uncertainty’s change with knowledge granularity, and also provide another new possible approach to the establishment of the machine learning model of fuzzy Petri net.
attributive abstraction and integration; qualitative mapping; attribute information granulation; fuzzy Petri net; knowledge reasoning
1 Introduction
In 1965, Lotfi A. Zadeh proposed the fuzzy set theory of fuzzy sets. In 1979, he first proposed and discussed the problem of fuzzy information granularity for the first time[1], and pointed out that there were three basic concepts constituting the basis of human cognition: granulation (dividing the whole into parts), organization (combine parts into the whole), and causation (association of cause and result). The granular computing exactly simulates these three functions of the human brain. Lotfi A. Zadeh also believes that human beings mainly use languages to think, judge and reason mainly with the language, and language itself is ‘granularity’. Word computing means how to judge with the language. The basis of word computing is knowledge granulation, and the core is fuzzy logic[2,3]. The essence and specific method to determine the concept of membership function, which is the cornerstone of the fuzzy set theory, have always been unclear, and even Lotfi A. Zadeh himself only specifies the approximate membership function with the qualitative reasoning method. Once the membership function is rigidly expressed as an accurate numerical through assumption, it is forced into the realm of exact mathematical. Therefrom, there is no fuzzy at all in the narrative of definition and theorem of the concept, proof of the theorem and other links of mathematical thinking[4]. People try to use various methods to solve the limitation of fuzzy logic, with common methods including the variable fuzzy set theory[5,6], extension set[7,8], cloud model[9], neutrosophic logics[10-12], etc.
The literature[13,26,28,29]puts forward the method of attribute theory, tries to explain the nature of fuzzy by introducing the qualitative mapping, and to describe the variability of fuzzy membership function in uncertainty. The attribute theory, from the perspective of qualitative criterion transformation, establishes the attribute coordinate system, gives a formal description of the essence and principle of variable fuzzy criterions, and establishes variable fuzzy sets based on the criterion, providing a way to explain the law of quantity-to-quality and its qualitative mapping for the philosophical and epistemological roots of fuzzy sets. The study shows that, by constructing the qualitative criterion space based on the attribute coordinate system, we can induce a fuzzy set, which can construct the factor space by topological division of the fine granularity. Under the framework of qualitative criterion changes, the fuzzy set theory, factor space theory and other granule computing theories can be expressed in the framework of attribute coordinates, through the linear stretch, translation and superposition of the qualitative criterion, as well as the change of topological parts (or granularity breakdown).
Based on the method of attribute theory, this paper proposes the model of attribute information granule and, discusses the problem of fuzzy granulation of attribute information granule. To explain the concept of information granule given by Lotfi A. Zadeh, it can be explained with an attribute and its qualitative mapping operator, thus simulating part of the cognitive functions of the human brain with the computing of the attribute granule. Meanwhile, we also discuss the reasoning of granulation form of attribute fuzzification information which is based on the fuzzy Petri net. We mainly use the fuzzy Petri net as a tool for formal reasoning here, with the main reason that the fuzzy Petri net is a kind of well-structured formal method with a good structure which is characterized by asynchronization, concurrency, uncertainty, etc. It is similar to some of the cognitive activities of the thinking process of human brain. If the library and the transition in the fuzzy Petri net are simulated by the attribute granule and the qualitative mapping respectively, then the fuzzy Petri net can be used to express the basic characteristics of a cognitive system through the method of attribute granule computing, such as knowledge representation, knowledge reasoning, learning patterns, memory patterns, etc. The results of this paper provide an interpretation framework for establishing the granular logic model in the uncertain problems and revealing the laws of knowledge uncertainty’s change with knowledge granularity, and also provide another new possible approach for establishing the machine learning model of fuzzy Petri net.
2 Attribute Information Granules
2.1 Basic concept of attribute computing
Conceptually, attribute is the characteristic expression of a thing and a quantity to describe the feature or nation of an object. To describe an object in a language closer to the natural language, it bridges the semantic gap between the object’s high-level category label and the low-level feature to a certain extent. In recent years, attribute learning has become a new research focus in the fields of machine learning and pattern recognition[14]. The deep learning of the attribute essentially aims to learn more useful features by building a machine learning model with multiple hidden layers and massive training data, thus eventually improving the precision of classification or prediction. Therefore, ‘deep learning models’ are means, and ‘feature learning’ are ends. Deep learning highlights the importance of the feature learning. In other words, through feature transformation layer by layer, a feature of a sample is transformed from original space to new space to make classification or prediction much easier[15-17].
From the perspective of human cognition, the attribute of a thing is a sensory information source and a sensory information processing unit for human being[19]. The attribute runs through the sensory feature extraction, perceptual image integration and memory model induction[20]. Thinking construction is a course that human brain receives and processes the attributes of things. The attribute is the essence expressed by a thing when it is related to other things, and therefore, only the attribute can reflect the thing itself and the relation with other things. The truth is, all messages received and processed by human being are attributes of things in terms of status, function, structure and relation. By processing the attributes of a thing, human not only can get the true understanding of the thing, but also create thinking or memory models such as status model, relation model, structure model and function model[21,22].
Neuroscience experiments indicate that sensory (at least visual and auditory) simple cells can quantitatively measure the value of their sensitive attributes, and that cortical cells can extract feature values of their sensitive attributes[23,24]. The theory of multi-stage integration developed by Semir Zeki points out that the complex sensory attributes and perceptual images are formed through multi-stage integration[25]. Accordingly, Document[32]proposes a sensory nerve testing model based on attribute value test and feature extraction, and discusses the primary two forms of attribute computing: attribute integration and attribute extraction.
2.1.1 Attribute computing and attribute category



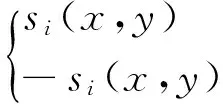
(1)
Whensi(x) is a single attribute ofT(x), the result issi(x,y), then we can say, Δ is an attribute extraction operation, or Δ is an integration operator.
In formula (1),si(x,y) ∈M(y) is the sensory image ofsi(x) inM(y). The formula (1) indicates that: ifT(x) contains attributesi(x) which can be detected bysi(y), thensi(y) will separate and extractsi(x) fromT(x) and detect whether imagesi(x,y) is inM(y), otherwise,si(y) tells the brain thatxdoes not have attributesi(x).
Based on the above definitions, Document[26]gives the following perceptual homomorphism lemma: if and only if perceptual mappingfis the homomorphism between the attribute setMxofXand the memory setM(y), the integration-based structure generated among attributes of objectXcan be maintained inM(y).
For example, ‘This table has four legs’, in the sense of the image is also ‘This table has four legs’.
The graphical representation of the perceptual homomorphism mappingfis showed in Fig.1.
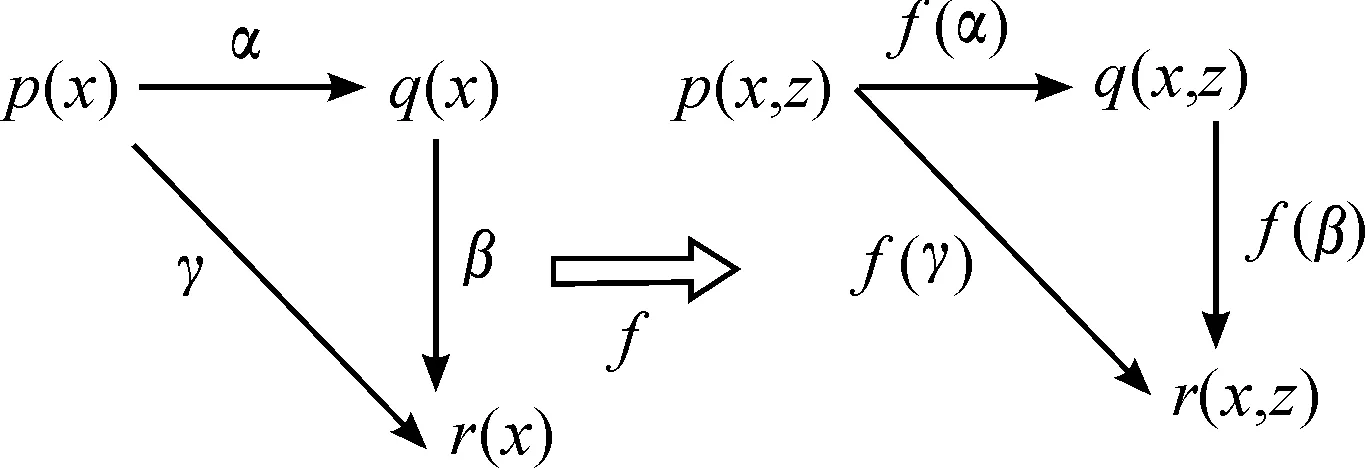
Fig.1 Perceptual homomorphism



r(a(x),b(x))*r(b(x),c(x))=r(a(x),c(x))
(2)
Inference2 Attribute setMxand attribute reasoning preorder can constitute an attribute preorder category Cr(Mx, →).
In fact, if let the element in homomorphism sets hom (a(x),b(x)) of object class obCr(x)=Mxin category Cr(Mx, →) be attribute reasoning preorder, it is obvious that homomorphism sets are integratable, identically equal, associative and disjointing.

Inference3 If and only if an absorption relation exists betweena(x) andb(x), the reasoning relation “a(x)→b(x)” in attribute setMxis true.
An attribute simplexK(x) and the subdivision complex of its barycenterK(m)(x) can be established to describe the formalization method for attribute computing.
The procedure for algorithm of attribute simplexK(x) is as follows.





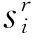

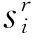
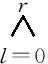
where,j=0, 1, …,n, that is,jmay be any base attribute element in the base attribute setMx.

f(pi(x))=f[T(pi(x)→e0(x)),…,T(pi(x)→en(x))=
(3)
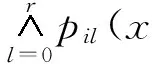

Theorem3[26]Attribute coordinate systemK(m)(x) is a linear coordinate system where the origin ise0(x), axis is base attributesei(x) and scale is weightdi(x) of base attribute.

In the attribute coordinate system, the proper subset relations among simplexes directly correspond to the absorption relations among their barycenter attributes, and therefore, the reasoning rules among data attributes of objectXcan be expressed as follows.
Rule1 If the attributeq(x) is located at the barycenter point of a certain sub-simplex of the simplexs(p(x)) which corresponds to the attributep(x), the attribute reasoning ‘p(x)→q(x)’ is true.
Rule2 If attributep(x) is the integrated attribute of all peaks of the simplexs=(q0(x),q1(x), …,qn(x)) which is composed of attributesqi(x), the attribute reasoning ‘(qi(x)→p(x)’ is true.
Example1 Group attribute G depends on the attributesGi(i=1, 2, 3, 4) of four groups.G1refers to the attribute that the operation is closed;G2refers to the attribute that the operation is associative;G3refers to the attribute that there are identity elements; andG4refers to the attribute that each element is reverse. Therefore,G=∧Giis true. If the four attributesGiare taken as peaks to establish a three-dimensional sub-simplexK(3)(G), the semi-group attributeSis located at the barycenterp(t1) of the one-dimensional simplext1=(G1,G2), monoid attributeMat the subdivision barycenterp(t2) of the two-dimensional simplext2=(G1,G2,G3), and group attributeGat the subdivision barycenterp(t3) of the three-dimensional simplexK=(G1,G2,G3,G4).As shown in Fig.2.
If an attributeG5(refers to the attribute that the operation is commutative) is added, then an Abel group is obtained. This is subdivision operation in the four-dimensional space.
Theorem4[26]K(m)(x) and its proper subset preorder relation constitute the Preorder CategoryC(K(m)(x), ≤).
Complex graphs are often composed of some basic structures[27,28], such as color can be adjusted by the three primary colors in accordance with a certain ratio. This rule exists not only in image, but also in sound. Experts discover 20 basic sound structures from unlabeled sounds, which can synthesize other sounds. Here, we can call these 20 basic sound structures as base attributes with which all other sounds can be synthesized. We can establish an attribute simplexK(x) for all these 20 base attributes, and all sound structures synthesized from these base attributes can be expressed in the subdivision complexK(20)(x)ofK(x).
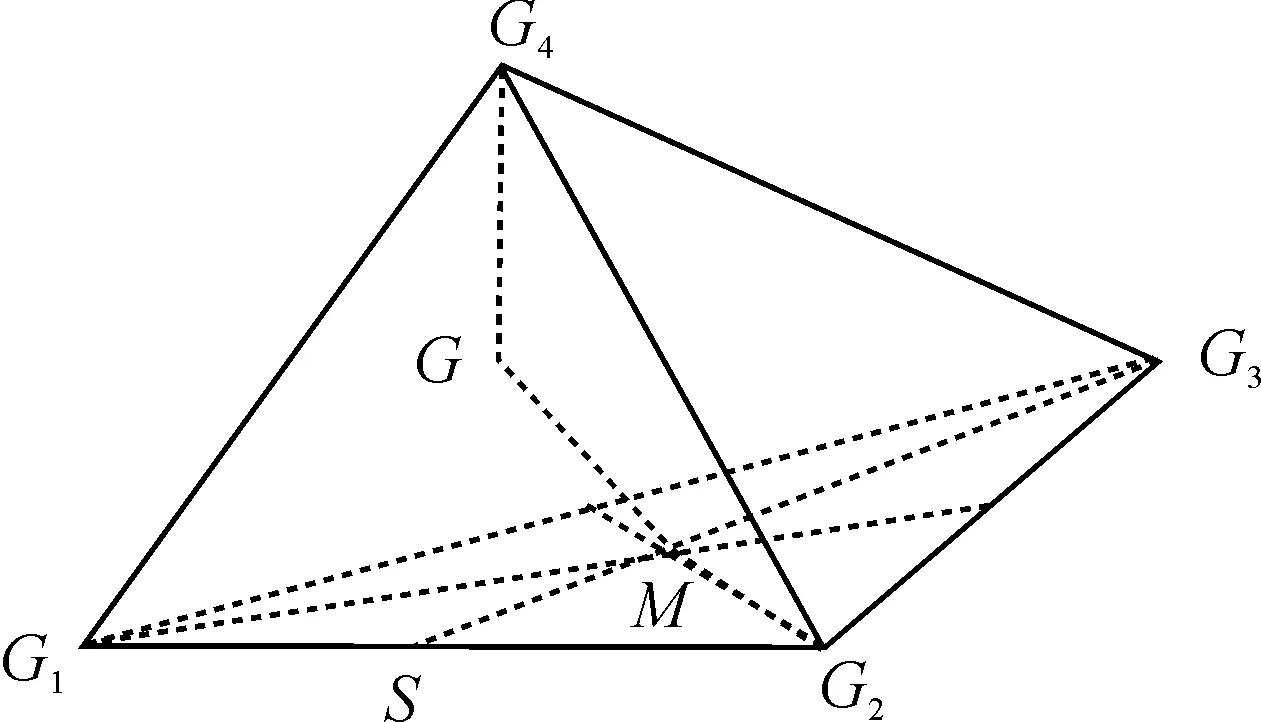
Fig.2ThesubdivisioncomplexofbarycenterforgroupattributeG.
2.1.2Qualitativemappingandattributetopologicalspace
Judgment is a form of thinking whereby one evaluates an object to make a decision. Every object has certain attributes. Judging an object is identifying or denying whether the object has (or doesn’t have) certain attribute[29]. Therefore, judgment in general can be called as qualitative judgment. Qualitative mapping is a mathematic expression of qualitative judgment. Starting from the law of mutual change of quality and quantity in philosophy, qualitative mapping, based on sensory feature extraction and according to the relation between quality, quantity and extent of things, is a mathematic model of brain thinking[3]. In the view of qualitative mapping, sensory feature extraction is the first step for human brain to form feeling and awareness by converting external information into in-brain information, and the essence of the sensory feature extraction is to convert the quantitative features of the attribute which are sensitive to the receptor cells into the quality features of the attribute which can be felt and recognized by cortical cells. Eventually, the quantity-to-quality transformation of the attribute during the sensory feature extraction and the transformation differences are abstracted into quantitative mapping and quantitative transformation degree function, which have been well applied to many fields such as XOR, double helix, classification, decision support and model recognition[29].
Seta(x) be the attribute of sensation of objectxand the quantitative and qualitative attribute values ofa(x) areda(x)andPa(x)respectively. If the qualitative attribute value ofxisPa(x), we can say thatxhas the property ofp(x) referred inPa(x).
When the quantitative-qualitative transformation of the attribute is considered, the attribute integration operation can be stated as follows:

Definition5[21]Let [αi,βi] be a qualitative criterion neighborhood ofp(x). If ∀da(x)∈[αi,βi] is true, the attribute values ofPa(x)corresponding toda(x)are all described as propertyp(x).
Definition6[21]LetΓ={[αi,βi]|i∈I} be the variety of all qualitative criteria of propositionp, and mappingTij:Γ→Γbe the qualitative criterion transformation of propositionp. If there is [αj,βj]∈Γfor any [αi,βi]∈Γ, then:
Tij([αi,βi])=[αj,βj]
(4)
For example: For a proposition ‘He is tall’, the criterionL1=(175 cm, 195 cm) is given by Asians,L2=(178 cm, 200 cm) by Americans, andL3=(185 cm, 220 cm ) by Europeans. For an objectXi, judging ofZjmay be based on different backgrounds and with different criteria ranging fromL1toL3.

Obviously, under the transformation of qualitative criterion, the homogeneous relation is an equivalence relation.
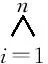
τ(x,[α,β])=x⊥[α,β]=
(5)
where, operator ⊥ means the operation of ‘testing whetherxfells in [α,β]’, so it is also called as ‘quantity-quality transformation operator’ or ‘qualitative operator for quality feature’. For the simplest judgment operation, operator ⊥ can be realized by “≦, ≧, <, >”.
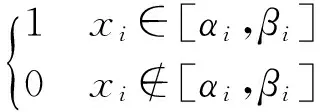
Example2 The range of normal human body temperature is 36.6~37.2℃, so the qualitative mapping operation for judging whether the body temperature is normal can be expressed as follows:
τ(t(pers),(36.5,37.2))=
t(pers)⊥(36.5,37.2)=
τnormal(t(pers))
(6)
In light of integration theory or logically, if abstract the qualitative criterion [α,β] in the above definitions into a setSand letpS(x) be the property that “xis an element ofS”, then the formula (5) above will be changed into the feature functionχS(x) of setSand:
Definition9[21]SetS⊆Xbe a subset of DomainX,P(X) be the set ofX’s powers, andpS(x) be the property that ‘xis an element ofS’. The mappingτp:X(P(X)→{0,1} is the qualitative mapping of propertypS(x) if ∃τp(x)∈{0,1} for ∀x∈Xto make the following be true:
(7)
where,τp(x,S) is the true value of propertypS(x).
In turn, if let setS={x} be the qualitative criterion of propertypS(x), then the feature functionχS(x) ofScan be regarded as the qualitative mapping of propertypS(x) withSas the qualitative criterion, that is:
(8)
Qualitative mappingτp(x,S) and feature functionχS(x) respectively use ‘x∈S’ to explain the connotation of propositionpS(x): ‘xis an element of setS’ and the extension of propositionpS(x): ‘Sis a set composed of all elementsxhaving the propertypS(x)’.
In topological space (X,P(X)),P(X) is the topology ofX. LetS(P(X) be an open subset or neighborhoodS(ξi,δi) which is determined with the distance from centerξiand radiusξi, then the qualitative mapping aboutpS(x) can be regarded as a mappingτp: (X,P(X)) → {0,1} from topological space (X,P(X)) to {0,1}.
Inference6 The qualitative mapping done in topological space (X,P(X)) is an attribute computing under cognitive model.
2.2Attributeinformationgranulesanditsstructure
The ideas of granular computing originate from Lotfi A. Zadeh, the founder of fuzzy mathematics, who first proposed the concept of information granularity in 1979 and gradually developed the theory of granular mathematics[30]. The intuitive understanding and explanation of the granular computing comprise the following aspects[31].
(1) Intuitive understanding of granule: A part separated from the whole in certain way can be seen as a whole granule. This is the concept of the granule. The combination of granules can be deemed as certain computing of granules.
(2) Intuitive understanding of granular computing: If a granule is seen as a part from the whole, then relation among granules, link between granules and the whole, combination of granules, transformation among granules, reasoning among granules, function of granules in describing other concepts, properties of granules can all be considered as granular computing in intuitive sense.
If all attributes of an object are seen as a whole, one single attribute among them can be seen as a granule. Attribute integration and extraction operation is a form of attribute granular computing. Qualitative mapping maps an attribute to a property, which is an intuitive attribute computing, also an intuitive granular computing. When we say objectxhas the propertyp(x) referred inPa(x)(quantitative features of attributea(x)), we actually mean that objectxhas the propertyp(x) under certain qualitative criterion. Therefore, richer semantic information can be expressed when attributes containing qualitative criterion or quantitative mapping are integrated into an attribute with a larger structure which we called attribute information granule or information granule for short.
Qualitative criterion can also be seen as a property of an attribute, so it is also a kind of information granule.
Definition10 In the topological space of an attribute, an information granule, based on the transformation of qualitative criterion, can be expressed in the form of a doublet.
(P,Γ) =(pi(x),[αi,βi]),or (P,Г)=
(da(x), [αi,βi])
(9)
where,a(x) is a sensory attribute of objectx,pi(x) is the attribute ofa(x), [αi,βi] is a qualitative criterion field ofpi(x), andda(x)is the qualitative attribute value of attributea(x).
The qualitative mapping value of anyx∈[αv,βv] equals to the true value of property propositionpv(o), so this is a one-to-one mapping and makes thesexform the same category [x]=[αv,βv]. If and only ifx,y∈[αv,βv], equivalence relationx←vyis true. And then, a quotient setX/~vof spaceXis identified by the equivalence relationx~vy, andX/~v=G([αv,βv]). Qualitative mapping can induce a quotient space, which is a granular computing to define the quotient space, so qualitative mapping is connected theoretically with quotient space.
The preorder reasoning of attributes is also a kind of information granular computing. Therefore, the granule category can be established in the attribute quotient space induced from qualitative mapping.
Definition11 Attribute information granule category determined according to qualitative criterion is seen as object category, homomorphism category formed by granular morphism category is called granular category and recorded as GcP. The object category is recorded as Obj(GcP), and the granular morphism category as Mor(GcP).

Attribute preorder reasoning is also a kind of granular computing[32,33]. According to Inference 2, the granular preorder category GcP (S(Mx,→)) can be obtained.
If a granule (pi(x),[αi,βi]) is simplified asΓi(pi), then an information granule is formally equivalent to a first-order predicate formula. The logic operation can be defined as follows.
Definition12 SetΓ(pi) andΓ(pj) be two information granules, the computing formula about logical connectives can be defined as follows:
① ~Γ(pi) =~(pi(x),[αi,βi])=(~pi,Γ′), whereΓ′ means the complement operation of qualitative criterion ofΓ;



Definition13 Semantic interpretation of the logical formula of information granule:
An interpretation is a quadrupleDas follows:
D={U,T,η, {Γi,i∈I}}
①Uis a nonempty set called domain of interpretation;
②Tis the mapping andP:U→U;
③ For anyi∈I,η:U×Γi→[0,1] is a degree function;
④Γiis qualitative criterion domain.
Under the interpretation ofD, each qualitative criterion transformation formulaPcorresponds to one elementv(P) in [0,1] which is called the true value ofPinD, where:
① IfPis logical formula of information granule (Γi(pi)=(pi(x),[αi,βi]), then:
② IfPis logical formula of information granule ~G, thenv(~G)=(v(G))′=v(~pi(x),Γ-[αi,βi]);
③ IfPis logical formula of information granuleG∨H, thenv(G∨H)=v(pi(x)▽pj(x),[αi,βi]∪[αj,βj]);

⑤ IfPis logical formula of information granuleG→H, thenv(G→H)=v(pi(x)⟹pj(x),[αj,βj]=T([αi,βi]))
v(G→H)=v(~G∨H);
where, ▽ refers to attribute disjunction operation; Δ, attribute conjunction operation; and ⟹, attribute reasoning operation.
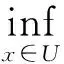
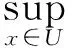
Definition14 Ifv(G)=v(H) (recorded asG=H) is always true when any value is appointed toD, then the ogical formula of information granuleGis equivalent toH.
Definition15 In the topological space of an attribute, if (pi(x)⟹pj(x)) is true and a mappingTij:Γ→Γexists to makeTij([αi,βi])=[αj,βj] be true, then (Γi(pi))→(Γj(Pj)) is a logical resoning in the information granule logic.
Definition16 In the topological space of an attribute, ifPjis located at the barycenter of a certain sub-simplex of the simplexs(pi) which correspondspi, then (Γi(pi)) →(Γj(Pj)) is a preorder reasoning in the information granule logic.
Definition17 In the topological space of an attribute, if (pi(x)(pj(x)) is true and a mappingTij:Γ→Γexists to makeTij([αi,βi])=[αj,βj] be true, then (Γi(pi)) →(Γj(Pj)) is a logical reasoning in the information granule logic.
Definition18 In the topological space of an attribute, ifPjis located at the barycenter of a certain sub-simplex of the simplexs(pi) which correspondspi, then (Γi(pi)) →(Γj(Pj)) is a preorder reasoning in the information granule logic.
3 Fuzzy Information Granulation
Lotfi A. Zadeh summed up the fuzziness as complexness of the system and stressed that fuzziness was ‘the uncertainty caused by the lack of clear transition from one category to another, rather than by randomness[34]. To identify the connection and difference between fuzziness and randomness, the transformation degree functionη(x) is introduced[26].
The closer the valuex∈[αi,βi] of attribute qualitative featurepi(o) is to the edge of [αi,βi], the more prone the qualitative change is to occur. In categorypi(o), the propertiespi(αi) andpi(βi)∈(pi(o) corresponding to the boundary pointsαiandβiare the most prone to transform to other qualitative feature (or property)pk(o), so they can be called critical properties in categorypi(o). Propertypi(ξi) is the most stable property in categorypi(o), which is the most unapt to transform into other qualitative feature and serves as the best representation of the essence of categorypi(o). Therefore, propertypi(ξi) is the intrinsic property ofpi(o), and pointξiis the intrinsic point ofpi(o). The followingk1(x) andk2(x) represent the extent of deviation of propertypi(x) (corresponding to objectx) frompi(ξi):
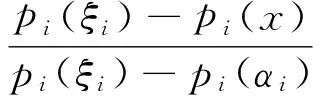
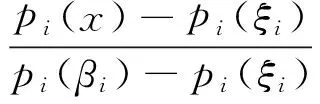
Then, theη(x) below is the closeness ofpi(x) to the intrinsic propertypi(ξi):
(10)
η(x) can also be called the transformation degree ofxqualitative feature categorypi(o).
Definition19[26]LetΓ=N(ξi,δi) be certain qualitative criterion domain of propertypi(x),δibe radius ofΓ,ξibe barycenter ofΓ, andX={x} be object set. The mappingη:X×Γ→[-1,1]iis the transformation degree function of qualitative feature categorypi(ξi) ofpi(x) if for ∀(x,N(ξi,δi))∈X×Γhas any ∃ηi(x)∈[-1,1]ito make the following formula be true:
η(x,ξi,δi)=|x-ξi|⊥δi=ηi(x)
(11)
where, the mathematics essence ofηi(x) is the difference between |x-ξi| andδi.
The value domain {0,1} of ordinary qualitative mappingτ(x) only has two values, soτ(x) only can express the logical relations in qualitative judgment based on attribute quantitative-qualitative feature transformation, without considering the transformation difference caused by quantity difference during the attribute quantity-quality transformation. However, the value domain of the transformation degree functionηi(x) has been expanded to [-1,1], so the difference in these quantitative-qualitative transformation degrees can be expressed mathematically. In addition, under some special transformation function, qualitative criterion originally fixed can become fuzzy. As a result, considering the difference between quantitative-qualitative transformations will lead to the fuzzification of information granule, i.e., fuzzy information granulation.
(12)
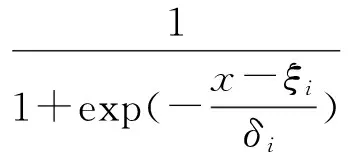
Definition20 In the topological space of an attribute, a fuzzy information granule, based on the transformation degree function of qualitative criterion, can be expressed in the form of a triplet:
G=((pi(x),[αi,βi],ηi(x)))
A fuzzy information granule represents a fuzzy concept or a fuzzy proposition. For example (soup water (60, 100], 0.9)), water is hot and has a temperature up to 90 ℃.
It is thus clear that the fuzzification of an information granule into fuzzy information granule can obtain more useful information from the original information granule. The fuzzification essentially is a course to identify the membership function of the fuzzy attributeG, or to determine the transformation degree function.
Based on the study on the dimension of subdivided category or granule, LotfiL. Zadeh defined the information granularity as a value of proposition[1]:xwhich is computed based on the membership ofλin the fuzzy subsetG⊆U, wherexis a variable onU, the value ofxis an entity onUwhich is written down as:g=(xisG)isλand formally recorded as:
g={the value (v(x)=uwherevis the assignment operator onU) ofu∈U:x, which is computed based on the membership ofλin the fuzzy subsetG⊆U.
Obviously, in the formula above, 0≤λ≤1. Based on fuzzy set theory, theλis a fuzzy membership function, and logically, theλis the fuzzy truth value or probability of the established proposition.
It can be easily figured out through comparison that: an information granule (pi(x),[αi,βi]) or (da(x),[αi,βi]) in definition 10, under the qualitative mappingτwith a transformation degree function, means that the computing that attributea(x) has the propertypi(x) is based on the membership of the attribute valueda(x)in the qualitative criterion [αi,βi], which has the same meaning as Zadeh did. This indicates that the definition of information granule concept given here is the same in meaning as that given by LotfiL. Zadeh.
4 Fuzzy Information Granules Reasoning
As an efficient tool for modeling and analysis, Petri net has developed in a rapid momentum in recent years, although it does not apply to many domains due to its pure theoretical nature[35,36]. A fuzzy Petri net is of broad significance when used to describe and analyze lots of parallel and concurrent behaviors in physical systems and even social systems as it is closer to human thinking and cognitive styles. It is especially applicable for human knowledge representation and artificial intelligence[37-40]. If tokens in a fuzzy Petri net are regarded as fuzzy information granules and translation as qualitative mapping or attribute quasi-ordered reasoning, then the fuzzy Petri net can, through fuzzy information granular computing, explore its application in knowledge representation, knowledge reasoning, learning model and memory model.
If a basic network element is used to simply represent qualitative mapping or single-step quasi-ordered reasoning, it can be represented in the form of a Petri net as shown in Fig.3.

Fig.3SimplePetrinetrepresentationofqualitativemapping.
To represent compositional operation of a qualitative mapping, its representation can be as Fig.4.

Fig.4 Compositional operation of a qualitative mapping.
Example3 A transition can be treated as a quasi-ordered reasoning, or mapping of a quasi-order category. Attribute semigroup in Fig.2 can be shown as the following Fig.5.
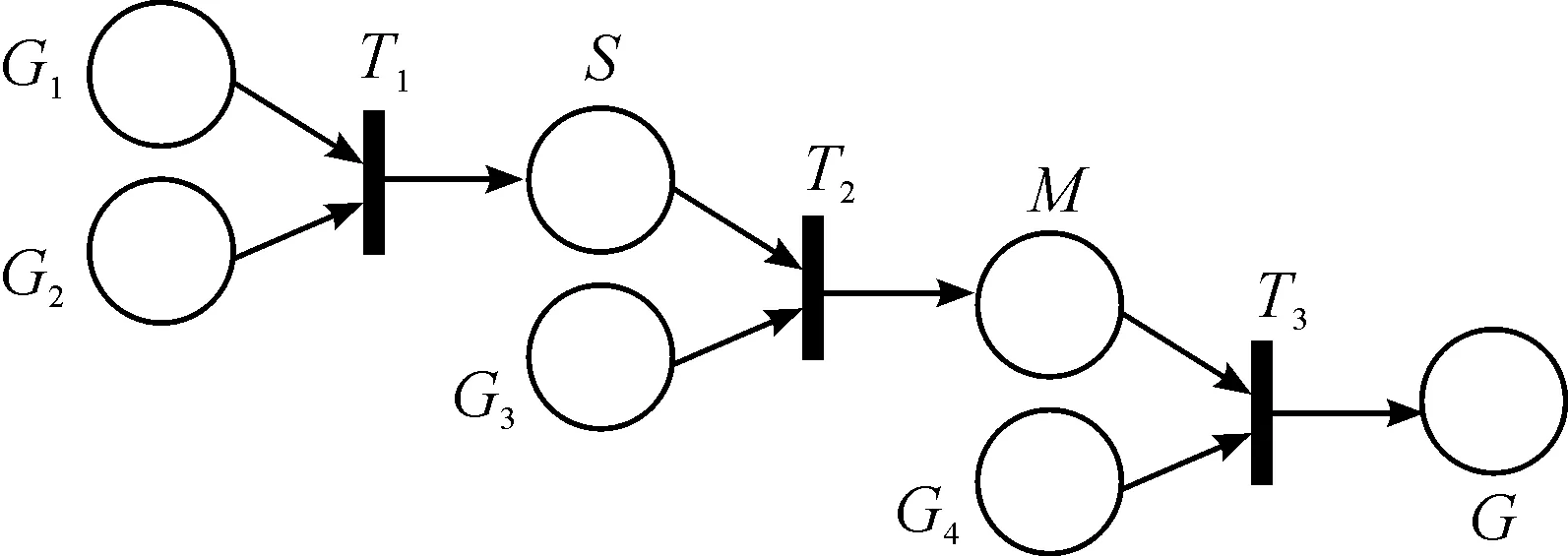
Fig.5 Petri net representation of semigroup G.
Where,T1,T2andT3are three quasi-order reasoning.
The transfer node in fuzzy Petri net can be intuitively treated as a qualitative mapping, and quantitative and qualitative properties and the field of qualitative criterion of an attribute of an object are mapped as tokens in the fuzzy Petri net. For qualitative criterion is also an attribute, token nodes in Fig.1 and 2 above can be extended as an information granule, and translation nodes are naturally granular transformation mapping. The reasoning model of fuzzy Petri nets defined based on a net element in Fig.1 is effective as for the attribute reasoning based on qualitative mapping and has relatively good reasoning capability for judgment-based recognition systems. Definition of the extended fuzzy Petri net form is as follows:
Definition21 A fuzzy Petri net applicable for attribute information granules fuzzy reasoning is as follows:
FIGPN= {P,T,F;M0,S,N,W,Γ}
(1) where,Pis the finite set of position nodes of a fuzzy information granule and also a finite set of position nodes of a quantitative (or qualitative) property of an attribute;
(2)Tis the finite set of transfer nodes of a fuzzy information granule, able to do operations of granular transformation, granular integration and granular composition;
(3)Fis a marked relation onP×T, indicating the connection from position nodes to transfer nodes, and rated input on the link;
(4)M0is a function defined onPwith the value being [0,K] (Kis a bounded real number), indicating the initial identification status of position nodes at the beginning of running;
(5)Sis the input strength calculation function;
(6)Nis the output strength function of qualitative degree function;
(7)Wis contribution weight of attribute and is the function ofΓ;
(8)Γis qualitative criterion;
Similar to this method, there are fuzzy cognitive graphs. As a kind of knowledge representation and reasoning technique, fuzzy cognitive graphs describe a system in a way that is close to people’s cognition[41- 43]. It expresses knowledge by emphasizing the causal connection and the structure of the graph, while using the rules to combine expert knowledge with the useful knowledge which is gained from the data.
A fuzzy cognitive map can be used to deal with non-monotonic reasoning and represent non-causality, but it is hard to represent uncertainties of measure of causality between concepts, time-space characteristic of causal connection, and uncertainty of knowledge by experts. There is a method for improvement: combination of a fuzzy cognitive map and the neural network to strengthen its reasoning function[44], though the fuzzy cognitive map and other improvement methods still fail to represent problems of reasoning that are built on the basis of variable fuzzy criterion. Extended fuzzy Petri nets can reasonably describe uncertainties and fuzziness in the real world. With its concurrent and asynchronous characteristics, the reasoning of the mentioned uncertainties can be described well, and meanwhile the cognitive mechanism of variable fuzzy criterion can be described through the extended fuzzy Petri net. The extended fuzzy Petri net reasoning is represented by the trigger of transition of weighted qualitative mapping, and the reasoning relation (quality-quantity-degree relations) between attributes by the directed arc between token and transition that is based on the weighted transformational degree function.
For FIGPN transition nodes, when operating, firstly compute the input strength on individual input links of transfer nodes (the input strength is a degree function of quantitative mapping with input and connection strength on input links as well as contribution weight of attribute); then compute a qualitative operator of qualitative characteristics defined to be on the individual input strength, which has the ability to ignite when the result exceeds the threshold.
The operational process of FIGPN is a problem solving process, during which the inference machine keeps computing the rate of contribution of new attributes through qualitative operation (using deduced qualitative property as a new attribute) based on existing knowledge in the attribute library and reference library, thus providing answers for what users are concerned. The operating mechanism of EFPN is an event-drive mode with attribute integration and extraction. Therefore, the so-called reasoning model actually shows the reasoning process of qualitative operation of qualitative mapping and degree transformation function.
When the logic deduction problem is converted into a Petri net model, in a set of Horn clauses, a target transition is potentially occurring if and only if a nonnegative T-invariant[37]exists. The process of finding T-invariants is actually the process of attributing clauses. However, due to a large amount of uncertain knowledge and rules in practical application, the traditional method of finding T-invariants is not practicable, therefore Xuhua Liu proposes theλ-Horn clause set description, and handles the reasoning ofλ-Horn clause set with theλresolution method[45]. In fact, the network structure and operation characteristics of the FIGPN are consistent with those of the fuzzy Petri. Therefore, theλattributing can also be implemented in the FIGPN, the process of which is the attribution process of attribute granular, whereλis given by the procedure function of the qualitative mapping. The reasoning process and the matrix algorithm for T- invariant are as follows.
The basic reasoning algorithm in FIGPN is as follows:
Cis then×mcorrelation matrix of APN model (the target transition corresponds to thenthrow inC), andEnis an identity matrix.
(1)A:=Cn×m;D:=En
(2) LOOPi=1 toi=m:
(a) Add any two lines of opposite element symbols which can be combined in rowiof the matrix A after the combined operation in the matrix [D/A], and put the corresponding combined substitution in each variable in the corresponding line, and add the newly added line in the [D/A].
(b) Delete lines for the operation in (a) of elements in rowiin A from [D/A].
(c) There is one element, a, greater thanλinA. If the row to which a correspond contains the same element, then delete the corresponding line.
END LOOP
The line less than or equal toDto whichλcorresponds inA, is the T-invariant of the correlation matrixC.
The paper[46]gives four different forms of the Horn clause and the corresponding Petri net model. An example is given to illustrate the effectiveness of FIGPN formal reasoning.
Example4 Any tableware sterilized with water of about 100 ℃ or acceptable special disinfectant or qualified disinfection cabinet is safe to use. If some tableware is known to have been sterilized with quite hot water or a bottle of dedicated disinfectant of a well-known brand (very reliable) or a relatively new disinfection cabinet, it is proved that the tableware is almost safe to use.
The above proposition is given in the form of attribute granule.
Let:Γ1(x):xis sterilized with water of about 100 ℃;Γ2(x):xis sterilized with special disinfectant;Γ3(x):xis sterilized with qualified disinfection cabinet;Γ4(x):xis qualified;Γ5(x):xis safe to use.
Prerequisite: ∀x((Γ1(x)∨Γ2(x)∨Γ3(x)) →Γ4(x)); ∀x(Γ4(x)→Γ5(x));η1Γ1(c);η2Γ2(c);η3Γ3(c)
Conclusion:η5Γ5(c)
where, (η1,η2,η3,η4)=(0.93,0.94,0.95,0.90), the degree value vector can be given by the qualitative degree functionηi(x).
Written in Horn clause set:
See Fig.6 for its FIGPN representation.
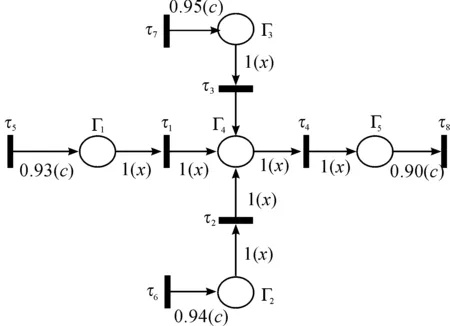
Fig.6 FIGPN reasoning of tableware sterilization.
Correlation matrix:
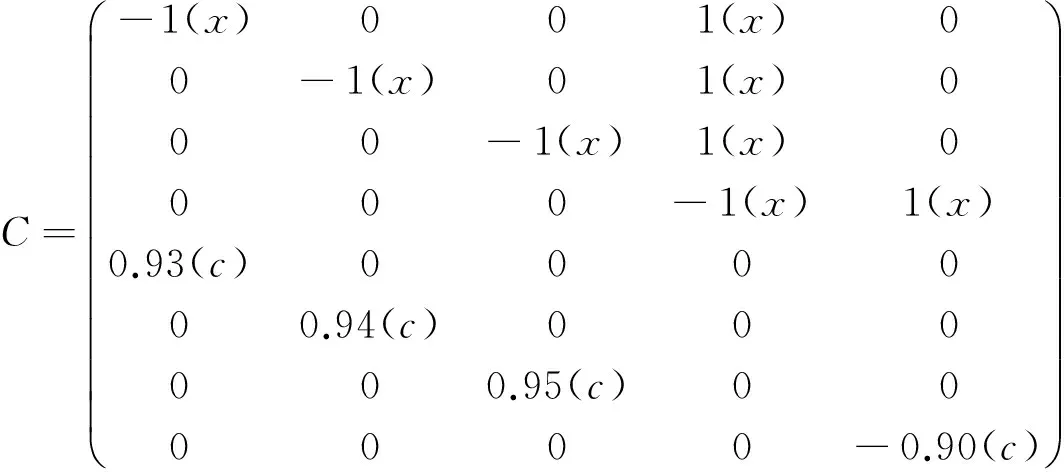
where, the row vector corresponds to (Γ1,Γ2,Γ3,Γ4,Γ5), and the line vector (τ1,τ2,τ3,τ4,τ5,τ6,τ7,τ8). The T-invariants are obtained by algorithm as follows:
① LetA:=C;D:=I8
② To attribute with the deletion strategy:
Because -0.07, 0.1 and 0 are all less thanλ=0.85, and it can be verified thatX={1,0,0,1,1,0,0,1} is the T- invariant of the correlation matrixC, and becauseX>0, so we come to the conclusion:η5Γ5(c).
5 Conclusion
The sensory organs of human beings receive a variety of sensory attribute information and respond differently. Things reflect their own state, movement and change process with their attributes and processes of change, and the human cognitive process is closely linked to these received attributes information. From the philosophical point of view, the attribute not only shows the qualitative features it wants to express, but also possesses the quantitative features that need it to define and regulate. Based on this view, this paper gives the basic mathematic model of the attribute information granule by combining the theory of granularity computing and the method of attribute theory, and discusses the problem of fuzzy information granulation and its formal reasoning in fuzzy Petri net. The research of computing of attribute information granule contributes to the study of knowledge representation, knowledge reasoning, learning mode, memory model, etc. This method can reflect the cognitive process with uncertain recognition and judgment to a certain extent, providing another way of thinking for exploring the application of granule computing to advanced intelligence and image-thinking ability of the human. This paper only gives a basic model framework, while a more complete research and application of the information granule and fuzzy information granulation theory based on the attribute computing is to be further researched.
Acknowledgment
This work is supported by the National Natural Science Foundation of China(60075016),the National High Technology Research and Development Program of China (863) sub project(2012AA101701-06),the Characteristic Innovation Project of Guangdong Universities(natural science)(Guangdong Education Science Letters[2015]No.3),open fund of Fujian Provincial Key Laboratory of Big Data Mining and Applications(Fujian University of Techology).
[1]L.A.Zadeh, Fuzzy sets and information granularity,AdvancesinFuzzySetTheoryandApplication,Amsterdam:North-Holland, vol.6, pp.3-38, 1979.
[2]L.A.Zadeh,Fuzzy Logic=computing with words,IEEETrans.Onfuzzysystems,vol.4,no.2, pp.103-111, 1996.
[3]L.A.Zadeh, Toward a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic,Fuzzysetsandsystems,vol.90,pp.111-127, 1997.
[4]D.Y.Li,C.Y.Liu, Y.Du,and X.Han,Artificial intelligence with uncertainty,JournalofSoftware,vol.15,no.11, pp.1583-1594, 2008.
[5]S.Y.Chen, Z.C.Xue, and M.Li,Variable Sets principle and method for flood classification,SciChinaTechSci,vol.56, pp.2343-2348, 2013.
[6]S.Huang,J.Chang, G.Leng, and Q.Huang,Integrated index for drought assessment based on variable fuzzy set theory: A case study in the Yellow River basin, China,JournalofHydrology,vol.527,no.8, pp.608-618, 2015.
[7]W.CAI, Extension theory and its application,ChineseScienceBulletin,vol.44,no.17,pp.1538-1548, 1999.
[8]A.Aledo Juan, A.Gamez Jose, and M.David, Using extension sets to aggregate partial rankings in a flexible setting,Appliedmathematicsandcomputation, vol.290,no.1, pp.208-223, 2016.
[9]D.Y.Li, K.Di, D.R.Li, and X.Shi,Mining association rules with linguistic cloud models,Journalofsoftware,vol.11,no.2,pp.143-158,2000.
[10] F.Smarandache,AUnifyingfieldinlogic:Neutrosophiclogic,NeutrosophicProbabilityandStatistics,USA:Xiquan Publishing Hours,2003.
[11] B.Kavitha, S.Karthikeyan, and P.S.Maybell, An ensemble design of intrusion detection system for handling uncertainty using Neutrosophic Logic Classifier,Knowledge-BasedSystems,vol.28,no.4,pp.88-96, 2012.
[12] U.Rivieccio, Neutrosophic logics:Prospects and problems,FuzzySetsAndSystems,vol.159,no.14,pp.1860-1868, 2008.
[13] J.L.Feng,A mathematical theory and method for thinking construction and intelligence modeling(An introduction of attribute theory and method),JournalofGuangxiNormalUniversity,vol.17,no.2,pp.1-7, 1999.
[14] E.R.Babbie,ThePracticeofSocialResearch,USA: Sworth Publishing, 2006.
[15] L.Deng and Y.Dong,Deeplearning:methodsandapplications.USA:NOW Publishers Inc,2014.
[16] Y.Bengio,Learning deep architectures for AI,FoundationsandtrendsinMachineLearning,vol.2,no.1,pp.1-127, 2009.
[17] G.E.Hinton and R.R.Salakhutdinov,Reducing the dimensionality of data with neural networks,Science,vol.313,no.5786, pp.504-507, 2006.
[18] D.Silver, A.Huang,and C.J.Maddison, Mastering the game of Go with deep neural networks and tree search,Nature,vol.529,pp.484-503,2016.
[19] J.Feng, Attribute network computing based on qualitative mapping and its application in pattern recognition,Journalofintelligent&fuzzysystems, vol.19,pp.1-16,2008.
[20] B.Yao,Qualityandquantity,Encyclopediaofphilosophy. China:China Encyclopedia publishing house,1989.
[21] J.Feng,Qualitative mapping,linear transformation of qualitative criterion and artificial neuron,InProceedingsoftheIJCAI-2007,workshoptheme:complexvaluedneuralnetworksandneuro-computing:novelmethods,applicationsandimplementations,Hyderabad,India, 2007,pp.4-47.
[22] J.Feng and Z.Wu, Conversion degree functions induced by qualitative mapping and artificial neurons, InProceedingsofICMLC2003,2003, pp.1135-1140.
[23] D.Hubel and T.Wiesel, Receptive fields and functional architecture in two nonstriate visual areas (18 and 19) of the cat,J.Neurophysiol., vol.28, pp.229-289, 1965.
[24] S.W.Kuffler, J.G.Nicholis, and A.R.Martin,FromNeurontoBrain, 2nd ed. Massachusetts: Sinauer Associates Inc, 1984.
[25] S.Zeki, The visual image in mind and brain,ScientificAmerican,vol.267,no.3, pp.68-77, 1992.
[26] J.Feng and Z.Dong,A Mathematical model of sensation neuron detection based on attributive abstraction and integration,Computerresearch&development,vol.34,no.7, pp.481-486, 1997.
[27] B.A.Olshausen and D.J.Field, Emergence of simple-cell receptive field properties by learning a Spare code for natural images,Nature,vol.381,pp.607-609, 1996.
[28] B.A.Olshausen and D.J.Field, How close are we to understanding V1?,Neuralcomputation,vol.17,no.8,pp.1665-1699, 2005.
[29] I.M.Copi and C.Cohen,Introductiontologic. USA:Routledge Press,2010.
[30] L.A.Zadeh,Towards a theory of fuzzy information granulation and its centrality in human reasoning and fuzzy logic,FuzzySetsandSystems, vol.19, pp.111-127, 1997.
[31] L.Yan,S.Wang,and D.Xue,Semantic reasoning study for rough logic about nary formulas,InProceedingsof2006IEEEinternationalconferenceongranularcomputing,Georgia,USA:IEEE Press, 2006, pp.381-384.
[32] J.Feng,Granular transformation of qualitative criterion,orthogonality of qualitative mapping system and pattern recognition,InProceedingsof2006IEEEinternationalconferenceongranularcomputing, Georgia,USA: IEEE Press, 2006, pp.10-12.
[33] W.Nie and J.Feng,The logic of qualitative judge mapping,Journaloffudanuniversity(Naruralscience),vol.43,no.5, pp.944-947, 2004.
[34] L.A.Zadeh, Fuzzy sets,InformationandControl,vol.8,no.3, pp.338-353, 1965.
[35] D.A.Zaitsev, Toward the Minimal Universal Petri Net,IEEETransactionsonSystems,Man,andCybernetics:Systems,vol.44,no.1,pp.47-58, 2014.
[36] J.Li, M.Zhou, and X.Z.Dai,Reduction and Refinement by Algebraic Operations for Petri Net Transformation,IEEETransactionsonSystems,ManandCybernetics,PartA:SystemsandHumans,vol.42,no.5,pp.1244-1255, 2012.
[37] V.R.L.Shen, Y.S.Chang, and T.Y.Juang,Supervised and Unsupervised Learning by Using Petri Nets,IEEETransactionsonSystems,ManandCybernetics,PartA:SystemsandHumans,vol.40,no.2,pp.363-375, 2010.
[38] L.Feng, O.Masanao, K.Takashi,and K.Kunikazu,A Learning Fuzzy Petri Net Model,IEEJTransactionsonElectricalandElectronicEngineering,vol.7,no.3,pp.274-282, 2012.
[39] A.A.Abed, A.A.A.Ali, N.Aslam, and A.F.Marhoon, A Robust Neural Fuzzy Petri Net Controller For A Temperature Control System,ProcediaComputerscience,vol.5, pp.881-890, 2011.
[40] H.C.Liu, Q.L.Lin, L.X.Mao,and Z.Y.Zhang, Dynamic Adaptive Fuzzy Petri Nets for Knowledge Representation and Reasoning,IEEETransactionsonSystems,Man,andCybernetics:Systems,vol.43,no.6,pp.1399-1410, 2013.
[41] B.Kosko,Fuzzy cognitive maps,InternationaljournalofMan-machinestudies,vol.24,pp.65-75, 1986.
[42] W.Pedryca,The design of cognivive in synergy of granular computing and evolutionary optimization,Expertsystemswithapplications,vol.37,no.10,pp.7288-7294, 2010.
[43] E.I.Papageorgiou and J.L.Salmeron, A review of fuzzy cognitive maps research during the last decade,IEEETransactionsonfuzzysystems,vol.21,no.1,pp.66-79, 2012.
[44] G.Acmpora and V.Lovia,On the temporal granularity in fuzzy cognitive maps,IEEETransactiononfuzzysystems,vol.19,no.6,pp.1040-1057, 2011.
[45] X.Liu and H.Xiao,Operator fuzzy logic and a-resolution,Chinesejournalofcomputer,vol.2,pp.82-91, 1989.
[46] C.Lin,A.Chaudhury, and A.B.Whinston,Logical Inference of Horn Clauses in Petri Net Models,IEEETransactionsonknowledgeanddataengineering,vol.5,no.3,pp.416-425, 1993.

Jia-liFengwas born in 1948.He is a professor and doctoral supervisor.He received his Ph.D degree from China Institute of Atomic Energy.He put forward attribute theory and method,a new theory and new method for thinking science and artificial intelligence.He presided over three National High Technology Research and Development Program of China(863).His current research areas include artificial intelligence, intelligent information processing and attribute theory method.

Hui-youChangwas born in 1962.He is now a professor and doctoral supervisor in Sun Yat-sen University.He received his B.S,M.S and Ph.D degrees from Harbin Institute of Technology,Harbin,China,in 1981,1984 and 1987,respectively.His current research areas include artificial optimization & Intelligent algorithm,data mining,complex problem modeling & algorithm,computer Integrated technology & application.

Yue-pengZhouwas born in 1982.He received his M.S. degrees from Liaoning University of Technology, Jinzhou, China.He is now a Ph.D. candidate in Computer Science and Technology of Sun Yat-sen University.His current research areas include Intelligent algorithm,data mining.
his M.S. degree in Computer technology from Guangxi Normal University.He is now a Ph.D. candidate in Computer Science and Technology of Sun Yat-sen University.He is also an assistant professor in Guangdong University of Education.His current research interests include machine learning, Intelligent information Processing,Petri net theory & aplication,Granular Computing.He is a senior member of the CCF.
•Ruqi Zhou is with Department of Computer Science, Guangdong University of Education, Guangzhou 510303, China.E-mail:ruqzhou@163.com.
•Jiali Feng is with College of Information Engineering, Shanghai Maritime University, Shanghai 200135, China.
•Ruqi Zhou, Huiyou Chang,and Yuepeng Zhou are with School of Data and Computer Science,Sun Yat-Sen University,Guangzhou 510006, China.
*To whom correspondence should be addressed. Manuscript
2017-05-15; accepted: 2017-06-22
 CAAI Transactions on Intelligence Technology2017年3期
CAAI Transactions on Intelligence Technology2017年3期
- CAAI Transactions on Intelligence Technology的其它文章
- Micro Structure of Injection Molding Machine Mold Clamping Mechanism: Design and Motion Simulation
- Retinal Image Segmentation Using Double-Scale Nonlinear Thresholding on Vessel Support Regions
- Enriching Basic Features via Multilayer Bag-of-words Binding for Chinese Question Classification
- Technology of Intelligent Driving Radar Perception Based on Driving Brain
- Technology and Application of Intelligent Driving Based on Visual Perception
- Interactions Between Agents:the Key of Multi Task Reinforcement Learning Improvement for Dynamic Environments
