Interactions Between Agents:the Key of Multi Task Reinforcement Learning Improvement for Dynamic Environments

Sadrolah Abbasi, Hamid Parvin, Mohamad Mohamadi, and Eshagh Faraji

InteractionsBetweenAgents:theKeyofMultiTaskReinforcementLearningImprovementforDynamicEnvironments

Sadrolah Abbasi, Hamid Parvin*, Mohamad Mohamadi, and Eshagh Faraji

In many Multi Agent Systems, learner agents explore their environments to find their goal and agents can learn their policy. In Multi-Task Learning, one agent learns a set of related problems together at the same time, using a shared model. Reinforcement Learning is a useful approach for an agent to learn its policy in a nondeterministic environment. However, it is considered as a time-consuming algorithm in dynamic environments. It is helpful in multi task reinforcement learning, to use teammate agents’ experience by doing simple interactions between each other. To improve performance of multi-task learning in a nondeterministic and dynamic environment, especially for dynamic maze problem, we use the past experiences of agents. Interactions are simulated by operators of evolutionary algorithms. Also it is switched to a chaotic exploration instead of a random exploration. Applying Dynamic Chaotic Evolutionary Q-Learning to an exemplary maze, we reach significantly promising results.

interactions between agents; multi task reinforcement learning; evolutionary learning, chaotic exploration; dynamic environments

1 Introduction

A Multi Agent System (MAS) usually is to explore or monitor its space to achieve its goal. In an MAS, each agent has only a local view of its own neighborhood. In these cases, each agent tries to learn a local map of its world. It is useful for agents to share their local maps in order to aggregate a global view of the environments and to cooperatively decide about next action selection. Therefore agents attempt to learn because they don’t know anything about their environment. The learning can happen in a cooperative background where the aim is to make agents to share their learned knowledge[1-8].

Multi-Task Learning (MTL)[10-15]is an approach in machine learning in that it tries to learn a problem together with other related problems at the same time, using a shared model. This often leads to a better model for the main task, because it allows the learner to use the commonality among the related tasks[13-19].

Also Reinforcement Learning (RL) is a type of agent learning that implies what to do in any situation or how to map situations to actions, in order to maximize agents’ reward. It does not tell the learners which actions to take and the agents must discover which actions yield the most reward. RL can solve sequential decision tasks through trial-and-error interactions with the environment. A reinforcement learning agent senses and acts in its environment in order to learn the optimal situation-to-action mapping to more frequently achieve its goal. For each action, the agent receives feedback (reward or penalty) to distinguish what is good and what is bad. The agent’s task is to learn a policy or control strategy for choosing the best set of actions in such a long run that achieves its goal. For this purpose, the agent stores a cumulative reward for each state or state-action pair. The ultimate objective of a learning agent is to maximize the cumulative reward it receives in the long run, from the current state and all subsequent next states along with goal state[20].

RL has two strategies for solving problems. (1) To use statistical techniques and dynamic programming methods to estimate the utility of taking actions in states of the world. (2) To search in the space of behaviors in order to find one that performs well in the environment. This approach can be achieved by Genetic Algorithms (GA) and Evolutionary Computing (EC)[21-26].

If the size of problem space of such instances is huge, instead of original Reinforcement Learning Algorithms, Evolutionary Computation could be more effective. Dynamic or uncertain environments are crucial issues for Evolutionary Computation and they are expected to be effective approach in such environments[27-31].

Q-learning is the specific families of Reinforcement learning techniques[32-37].This is a powerful algorithm for agents that are to learn their knowledge in a RL manner. It is worthy to mention that this algorithm is considered as one of the best RL algorithms. The only drawback of the Q-learning algorithm is its slowness during learning in an unknown environment.

Most of researches in the RL field focus on improving the speed of learning. It has been shown that Transfer learning (TL) can be very effective in speeding up learning. Main idea of TL is based on “experience gained in learning to perform one task that can help improve learning performance in a related, but different, task”. In TL, knowledge from some tasks is used to learn other tasks. The steps of a TL method is: “deconstructing the task into a hierarchy of subtasks, learning with higher-level, temporary abstract, actions rather than simple one-step actions; and efficiently abstracting over the state space, so that the agent may generalize its experience more efficiently”[1-5].

TL and MTL are closely related to each other. MTL algorithms may be used to transfer knowledge between learners, similar to TL algorithms, but MTL supposes all tasks that have the same distribution, while TL may allow for arbitrary source and target tasks. MTL generally does not need task mappings.

In MTL, data from multiple tasks can be considered simultaneously and it is possible that RL agents could learn multiple tasks simultaneously in a multi agent system. A single large task may be considered as a sequential series of subtasks. If the learner does each subtask, it may be able to transfer knowledge between different subtasks, which are related to each other because they are parts of the same overall task. Such a setting may provide a well-grounded way of selecting a distribution of tasks to train over, either in the context of transfer or in MTL[12-19].

In this work we found that using interactions between learner agents improves the performance of Multi Task Reinforcement Learning. In order to implement simple and effective interactions among the agents in a nondeterministic and dynamic environment, we have used genetic algorithm. Also, due to using GAs, it is possible to maintain the past experiences of agents and to exchange experiences between agents.

In the remaining of this paper, it can be found the literature review of this scope in next section. It contains reinforcement learning first. Then it explains evolutionary computations in RL. Finally it manages chaotic methods in RL.

Overall, our contributions in this work are:

• Employing interactions between learning agents by using an evolutionary reinforcement learning algorithm in support of increasing performance in both speed and accuracy of learning.

• Exploring the role of interaction existence in a dynamic maze learning.

• Implementation of multi-task reinforcement learning in a nondeterministic and dynamic environment.

• Regarding effect of chaotic exploration phase in quality of learned policy in a dynamic environment

2 Literature Review

2.1 Reinforcement learning

In Reinforcement learning problems, an agent must learn behavior through trial-and-error interactions with an environment. There are four main elements in RL system[16-22], i.e., policy, reward function, value function and model of the environment. A policy defines the behavior of learning agent and it consists of a mapping from states to actions. A reward function specifies how good the chosen actions are and it maps each perceived state-action pair to a single numerical reward. In a value function, the value of a given state is the total reward accumulated in the future, starting from that state. The model of the environment simulates the environment’s behavior and may predict the next environment state from the current state-action pair and it is usually represented as a Markov Decision Process (MDP)[21-31]. In a MDP Model, the agent senses the state of the world, then it takes an action which leads to a new state. The choice of the new state depends on the agent’s current state and its action.

An MDP is defined as a 4-tuple 〈S,A,T,R〉 characterized as follows: S is a set of states in environment, A is the set of actions available in environment, T is a state transition function in state s and action a, R is the reward function. Taking the best action available in a state is the optimal solution for an MDP. An action is best, if it collects as much reward as possible over time.

There are two classes of methods for reinforcement learning: (a) methods that search the space of value functions and (b) methods that search the space of policies. The first class is exemplified by the temporal difference (TD) methods and the second by the evolutionary algorithm (EA) approaches[31-43].

TD methods, such asQ-learning, learn by backing up experienced rewards through time.Q-learning method is considered as one of the most important algorithms in RL (Sutton et al., 1998). It consists of aQ-mapping from state-action pairs by rewards obtained from the interaction with the environment.

In this case, the learned action-value function,Q:S×A→R, directly approximatesQ*, the optimal action-value function, independent of the policy being followed. The current best policy is generated fromQby simply selecting the action that has the highest value from the current state.

Q(s,a)←Q(s,a)+a[r+γmaxa′Q(s′,a′)-Q(s,a)]

(1)

In equation 1,s,r,aandΓdenote state, action, learning rate and discount-rate parameter respectively. In this case, the learned action-value function,Q, directly approximatesQ*, the optimal action-value function, independent of the policy being followed.

The pseudo code ofQ-learning algorithm is shown in Algorithm 1. One policy for choosing a proper action isε-greedy. In this policy, the agent selects a random action with a chanceε, and the current best action is selected with probability 1-ε(whereεis in [0,1]).

Algorithm1Q-Learning

01 InitializeQ(s,a)arbitrarily02 Repeat(foreachepisode):03 Initializes04 Repeat(foreachstepofepisode):05 Chooseafromsusingpolicyderivedfrom Q(e.g.,ε-greedy)06 Takeactiona,observer,s'07 Q(s,a)←Q(s,a)+a[r+γmaxa'Q(s',a')-Q(s,a)]08 s←s'09 Untilsisterminal

Because of its slowness in nondeterministic and dynamic environments reinforcement learning, some secondary methods are used to improve learning performance in terms of both speed and accuracy. In this work, it has applied evolutionary algorithms and has employed chaotic functions in Q learning algorithm.

2.2 Evolutionary computations in RL

A large number of studies concerning dynamic or uncertain environments that have been performed so far have used Evolutionary Computation algorithms[4-6]. It tries to reach the goal as soon as possible in these problems. A significant issue that must be mentioned is that the agents could get assistance from their previous experiences.

As mentioned before, EC could be more efficient in a problem with a very large space and also in a dynamic or uncertain environment. In a research on MTL field, EC has been applied to RL algorithm[6-7]. In that case, a population of solutions (as individuals) and an archive of past optimal solutions containing each episode optimal solution are added to original structure of RL Algorithm. Individuals are pairs of real-valued vectors of design variables and variance. If the variance of the optimal value distribution is not so large, the MTL would be better, because of using past acquired knowledge of previous problem instances. The fitness function in EC algorithm is defined as total acquired rewards. The algorithm is presented in Algorithm 2.

Algorithm2ArchivebasedEC

01 Generatetheinitializepopulationofxin-dividuals02 Evaluateindividuals03 Eachindividual(parent)createssingleoffspring04 Evaluateoffsprings05 Conductpair-wisecomparisonoverpar-entsandoffsprings06 Selectthexindividuals, whichhavethemostwins,fromparentsandoffsprings07 Stopifhaltingcriterionissatisfied. OtherwisegotoStep3

Similar to Handa’s work (2007), in another research an approach to explore the optimal control policy for RL problem by using GAs is proposed[42]. Also each chromosome represents a policy. Those policies can be modified by genetic operations such as mutation and crossover. There are some variety compared with Handa’s algorithm such as chromosome setting, and GA operators.

An efficiency of Genetic Algorithm is that it can directly learn decision policies without studying the model and state space of the environment in advance. The only feedback for GAs is the fitness values of different potential policies. In many cases, fitness function can be expressed as the sum of rewards, which are used to update the Q-values of value function-based Q-learning algorithm.

In a recent work, Beigi et al. (2010) have presented a modified Evolutionary Q-learning algorithm (EQL). Also, they have shown there the superiority of EQL over QL in learning of multi task agents in a nondeterministic environment. They uses a population of potential solution in the process of learning of agents. The algorithm is exhibited in Algorithm 3.

Thus, Evolutionary Reinforcement Learning (ERL) is a method of probing the best policy in RL problem by applying genetic algorithms and in this work it tries to consider the effects of simple interactions presence between agents and experience exchanges between partial solutions.

2.3 Chaotic methods in RL

One of the challenges in reinforcement learning is the tradeoff between exploration and exploitation. Exploration means trying actions that improve the model, whereas exploitation means behaving in the optimal way given the current model. To obtain a lot of reward, a reinforcement learning agent must prefer actions that it has tried in the past and has found to be effective in producing reward. But to discover such actions, it has to try actions that it has not selected before. In other word, Exploitation is the right thing to do and to maximize expected reward on the one play, but exploration may produce greater total reward in the long run. The exploration-exploitation dilemma has been intensively studied by mathematicians for many decades[43].

Algorithm3EQL

01 InitializeQ(s,a)byzero02 Repeat(foreachgeneration):03 Repeat(foreachepisode):04 Initializes05 Repeat(foreachstepofepisode):06 ChooseafromsusingpolicyderivedfromQ (e.g.,-greedy)07 Takeactiona,observer,s'08 s←s'09 Untilsisterminal10 AddvisitedpathasaChromosometoPopulation11 Untilpopulationiscomplete12 DoCrossover()byCRate13 EvaluatethecreatedChilds14 DotournamentSelection()15 Selectthebestindividualforupda-tingQ-Tableasfollows:16 Q(s,a)←Q(s,a)+a[r+γmaxa'Q(s',a')-Q(s,a)]17 Copythebestindividualinnextpopulation18 Untilsatisfyingconvergence

The schema of the exploration is called a policy. There are many kinds of policies such asε-greedy, softmax, weighted roulette and so on.ε-greedy is a simple approach that tries to balance between exploration and exploitation. In these policies, exploring is decided by using stochastic numbers as its random generator.

Chaos theory studies the behavior of certain dynamical systems that are highly sensitive to initial conditions. Small differences in initial conditions (such as those due to rounding errors in numerical computation) result in widely diverging outcomes for chaotic systems, and consequently obtaining long-term predictions impossible to take in general. This happens while these systems are deterministic, meaning that their future dynamics are fully determined by their initial conditions, without random elements involved. In other words, the deterministic nature of these systems does not make them predictable if the initial condition is unknown[1-5].

However, it is known that chaotic source also provides a random-like sequence similar to stochastic source. Employing the chaotic generator based on the logistic map in the exploration phase gives better performances than employing the stochastic random generator in a nondeterministic maze problem[6-9].

In a research in this scope[5], it has shown that the usage of chaotic pseudorandom generator instead of stochastic random generator results in a better exploration. In that environment, goals or solution paths are changed along with exploration. Note that the foresaid algorithm is severely sensitive to value ofεinε-greedy. It is important to note that it has not used chaotic random generator in nondeterministic and dynamic environments.

As it is mentioned, there are many kinds of exploration policies in the reinforcement learning. It is common to use the uniform pseudorandom number as the stochastic exploration generator in each of the mentioned policies. There is another way to deal with the problem of exploration generators which is to utilize chaotic deterministic generator as their stochastic exploration generators[42].

In a previous work[43], a chaotic based evolutionary Q learning method (CEQL) is introduced to improve learning performance in both speed and accuracy in a nondeterministic environment. In that paper, a logistic map is used according to equation 2 as the chaotic deterministic generator for stochastic exploration generators. It leads to generate a value in the closed interval [0 1].

xt+1=ηxt(1-xt)

(2)

In equation 2,x0is a uniform pseudorandom generated number in the [0 1] interval andηis a constant chosen from [0 4]. It can be illustrated that sequencexiwill be converged to a number in [0 1] provided that the coefficientηis a number near to and below 4[41-43].It is important to note that this sequence may be divergent for theηgreater than 4. The closerηto 4, the more different convergence points of the sequence. Ifηis selected 4, the vastest convergence points (maybe all points in the [0 1] interval) will be covered per different initializations of the sequence. The algorithm of CEQL is presented in Algorithm 4.

Algorithm4CEQL

01 InitializeQ(s,a)byzero02 Repeat(foreachgeneration):03 Repeat(foreachepisode):04 Initializes05 Repeat(foreachstepofepisode):06 Initiate(Xcurrent)byRnd[0,1]07 Repeat08 Xnext=η*Xcurrent*(1-Xcurrent)09 Until(Xnext-Xcurrent<ε)10 ChooseafromsusingXnext11 Takeactiona,observer,s'12 s←s'13 Untilsisterminal14 AddvisitedpathasaChromosometoPopulation15 Untilpopulationiscomplete16 DoCrossover()byCRate17 EvaluatethecreatedChilds18 DotournamentSelection()19 Selectthebestindividualforupda-tingQ-Tableasfollows:Q(s,a)←Q(s,a)+a[r+γmaxa'Q(s',a')-Q(s,a)]20 Copythebestindividualinnextpopula-tion21 Untilsatisfyingconvergence

3 Interaction Between Agents

An interaction occurs when two or more agents are brought into a dynamic relationship through a set of reciprocal actions. During interactions, agents are in contact with each other directly, through another agent and through the environment.

Multi-Agent Systems may be classified as containing (1) NI-No direct Interactions, (2) SI-Simple Interactions and (3) CI-Complex, Conditional or Collective Interactions between agents. SI is basically one-way (may be reciprocal) interaction type between agents and CI could be conditional or collective interactions. In NI, agents do not interact and just do their activities with their knowledge. In such models of MAS, inductive inference methods are used.

Some forms of learning can be modeled in NI MAS, in this case the only rule is: “move randomly until finding goal”. Agents learn from evaluating their own performance and probably from those of other agents, e.g. looking at other agents’ behavior and how they choose the correct actions. Therefore, agents learn either from their own knowledge or from other agents, without direct interaction with each other.

Basically, while the RL framework is designed to solve a single learning task, and such a concept as reuse of past learning experiences is not considered inside it, there are lots of cases where multiple tasks are imposed on the agents.

In this paper, we try to apply interactions between learning agents and use the best experiences that have achieved by agents during multi task reinforcement learning.

4 Implementation

4.1 Maze problem

It is supposed that there are some robots in a gold mine as workers. The tasks of robots are to explore the mine to find the gold that is in an unknown location, from the start point. The mine has a group of corridors which robots can pass through them. In some of corridors, there exist some obstacles which do not let robots continue. Now, assume that because of decadent corridors, it is possible that in some places, there are some pits. If a robot enters to one of the pits, it may be unable to exit from the pit by some moves with a probability above zero. If it fails to exit by the moves, it has to try again. It makes a nondeterministic maze problem. The effort is to find the gold state as soon as possible. In such problems, the shortest path may not be the best path; because it may have some pit cells and it leads agent act many movements until finding goal state. Thus the optimum path has less pit cells together with shorter length.

The defined time to learn a single task is called Work Time (WT). In such nondeterministic problem, it is supposed that the maze is fixed in a WT. during a WT; agent explores its environment to find the goal as many times as possible during learning.

In this situation, imagine that there are some repairing men to fix some pits that have been seen at the end of a WT. But as corridors decadent, it is possible that some pits have been created randomly in the same or other locations in mine corridors before the beginning of next WT. Nonetheless, the main structure of maze is the same, but locations of pits may be changed. In other words, through a certain WT, locations of pits are fixed and in next WT, the locations of pits may be changed. Note that, the number of pits is the same in all WTs.

Consequently, robots start to learn their environment at the beginning of a WT. They have to learn their environment for a long time. Because of the similarity existing between tasks, this problem can be considered as a multi task learning problem.

Task of a robot in a WT is like other tasks in next WTs. The structure of maze is the same but some environmental changes may have done. In this way, if robots try to apply their past achieved knowledge during learning, they can do their task faster. Hence it is an appropriate approach for robots to use their past experiences to find defined goals.

In mentioned dynamic version of mine problem, it is possible to repair the pits immediately even during a WT but some other pits may be generated in other locations. It means that, in dynamic version of the problem, a number of pits are fixed but their locations may be changed.

It is necessary to have interactions between agents to exchange the promising experiences achieved through trial-and-error exploring of the maze. A simple interaction approach can be modeled by evolutionary computations.

4.2 Simulation

Sutton’s Maze[2]is a well-known problem in reinforcement learning field and many researchers in this scope are validated their methods via Sutton’s Maze. The original Sutton’s maze problem consists of 6×9 cells, 46 common states, 1 goal state and 7 collision cells which are depicted in Fig.1. Start and goal states are shown with ‘S’ and ‘G’ letters and collision cells are indicated with grey color.

Fig.1 Original Sutton’s maze.

Each time, agents move from start state and explore the maze to find the goal state. Agent can move to its neighbor cells with the defined action: Up, Down, Left, and Right. It can’t pass through collision cells and can’t exit the maze board. The original Sutton’s Maze problem is a deterministic problem.

To simulate the mine maze, as a nondeterministic and dynamic problem, a modified version of Sutton’s maze is presented. In nondeterministic version, a number of Probabilistic Cells (PC), which is depicted by hachure in Fig.2, is added to the original one. An agent can’t leave each of the probabilistic cells by its taken actions certainly and the probability of remaining in the same states is greater than zero. Hence if an agent is located in such PCs, despite of its chosen actions to move through the maze, it may stay in the same cell with a positive (above zero) probability. Note that the probability of moving is equal to “1-probability of stay”.

Fig.2 Modified Sutton’s maze.

An agent initiates from start state and explores the maze through taking some actions. It will gain a reward +1, if it reaches goal state. All other states don’t give any reward to agent. There is no punishment in this problem.

Each action in this space could be modeled by an MDP sample such as delineated in Fig.3. Right part shows an MDP model of certain case in which agent moves to next state by choosing any possible action with a probability equal to 1. Conversely, the left part reveals that it is possible that the agent can’t move to a neighbor state by choosing a possible action and it may remain in its position. For example, according to Fig.3, if an agent is in the PC and takes “Up” action, next state may be the same state with probability equal to 0.2. It is clear that Fig.3 shows the situations of states that are not boarder cells or have no obstacle in their neighborhood. Otherwise, the MDPs have less next states.

In nondeterministic case, the values of probabilities corresponding to every action in PCs are sampled from a normal distribution with averageμ=0 and varianceσ=1 according to equation 3.

(3)

These MDPs presented to learning algorithm sequentially. The presentation time of each problem instance is enough to learn. The aim is to maximize the total acquired rewards for lifespan. Agents are returned to start state after arriving goal state or after finishing the lifetime.

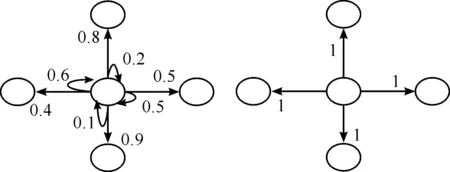
Fig.3 Actions MDP models.

In this problem, there are multiple learning tasks and it is essential for the agents to keep their best past experiences and utilize them in the current learning task to solve the tasks faster. Generally in RL, it costs a large number of learning trials, and then exploiting them seems to be promising as it could reduce the number of learning trials significantly. Here multiple tasks are defined through the distribution of MDPs, and a learning agent maintains and exploits the value statistics to improve its RL performance. Based on this, applying evolutionary reinforcement learning is more useful for such problems.

In this work, we evaluated the proposed method on a problem that defined as a multi task reinforcement learning example. In this example, agents learn their nondeterministic and dynamic environment by chaotic based evolutionaryQlearning algorithm.

5 Experiments and Results

Two sets of experiments have been done in nondeterministic and dynamic cases. In both of them, the number of PCs is equal to 25. A single experiment is composed of 100 tasks. Each task presents a valid path policy of an agent from start point to goal and contains a two dimensional array of the states and actions which the agent has visited. A valid path is the track of agent states from start to goal states, if agent has achieved the goal before defined Max Steps. In other word, if an agent can find the goal before defined Max Steps, its trajectory is accepted as an individual to insert to initial population. Through these chromosomes, past obtained experiences of agents is maintained. In this case, Max Steps is designated to 2 000. Each individual has a numeric value which is calculated by Value Function.

Value function tries to simulate an agent behavior in a given sequence of states. In this function to evaluate an individual, the Mainstream of agent movement is first extracted by eliminatoffing the duplications in path. It means the path only contains effective pairs of state-action which leads to state transition in agent’s trajectory. Second, the acquired mainstream is presented to an object and it is forced to follow the direction. Now the number of actions that object would do to end is accounted. This algorithm is executed for a certain time and the average of these paths’ size makes the value of the path. The existence of PCs in mainstream can cause a longer path. There is a relationship between the fitness and the inverse of value.

Population size is set to 100. In every experiment, 100 generation epochs are done. In every epoch, a two-point crossover method is used. In this method, two individuals are selected and two states in first individuals are determined randomly. Then, to seek first state from start and second state from end in second individual. After this, these sub-streams are swapped between individuals. Finally, children are evaluated and the best individual is kept. Due to this crossover method, agents can interact with each other and exchange the best experience to others.

Truncation selection is applied to the algorithm. After the last generation, the best chromosome is selected to update the state-space table in reinforcement learning algorithms (Four reinforcement learning algorithms include OQL, CQL, EQL and CEQL, as mentioned before). As discussed before, in this work, the value ofηin equation 2 is chosen 4 to make the output of the sequence similar to the uniform pseudorandom number.

In this work for both nondeterministic and dynamic cases and for any of four RL algorithms, 100 experiments have been done. Thus 4 000 000 generations in 100 experiments have been executed.

Table 1 summarizes the experiment results in nondeterministic mode. As it can be inferred from Table 1, by using interactions between agents and then applying the best achieved experiences (instead of no interaction mode), results in considerable improvement in all three terms of Best average, Worst average and Total average of path lengths. Also performing chaotic generator as a replacement of stochastic random generator improved the outcomes (results in tarred columns).

Table 1 Effect of using interactions between agents in nondeterministic environment.

The usage of evolutionary Q-learning in Original Q-Learning results in a 5.09% improvement. It has shown that the usage of chaotic pseudorandom generator instead of stochastic random generator results in a 6.85% improvement. This isn’t unexpected that the usage of interactions and experience exchanges and in addition, the chaotic generator in reinforcement learning algorithm can improve the results. Because it is explored in[13]before and the superior of chaotic generator over stochastic random generator in exploration phase of reinforcement learning has been shown. Also as it is reported in[14]that the evolutionary reinforcement learning can improve the average found paths significantly comparing with the average paths found by the original version.

Also it is shown here that the performance of using interactions in the form of evolutionary Q-learning can precede chaotic based Q-learning. So it can be expected that the employing of chaotic generator instead of stochastic random generator in evolutionary reinforcement learning can also yield a better performance.

As it is reported in Table 1, the average paths found by the chaotic based evolutionary reinforcement learning can be improved comparing with the average paths found by non-chaotic version of evolutionary reinforcement learning by 5.09% expectedly. So it can be concluded that leveraging the chaotic random generator in exploration phase of the reinforcement learning can be effective in a better environment exploration in both evolutionary base version and non-evolutionary one.

Experiments in dynamic mode, as explants in Table 2 are examined in all four modes, i.e., original, chaotic based, evolutionary, and chaotic based evolutionary Q learning. These tests are conducted in two phases. First phase is similar to nondeterministic experiments, that the agents learn their tasks in the same nondeterministic maze environment. Then in second phase, the environmental changes are done for 10 times and the agents have to find the goal in the same way without learning and relying on their past experiences every time. Table 2 is the summarization of these experiments. The proposed method has promising results in dynamic environments.

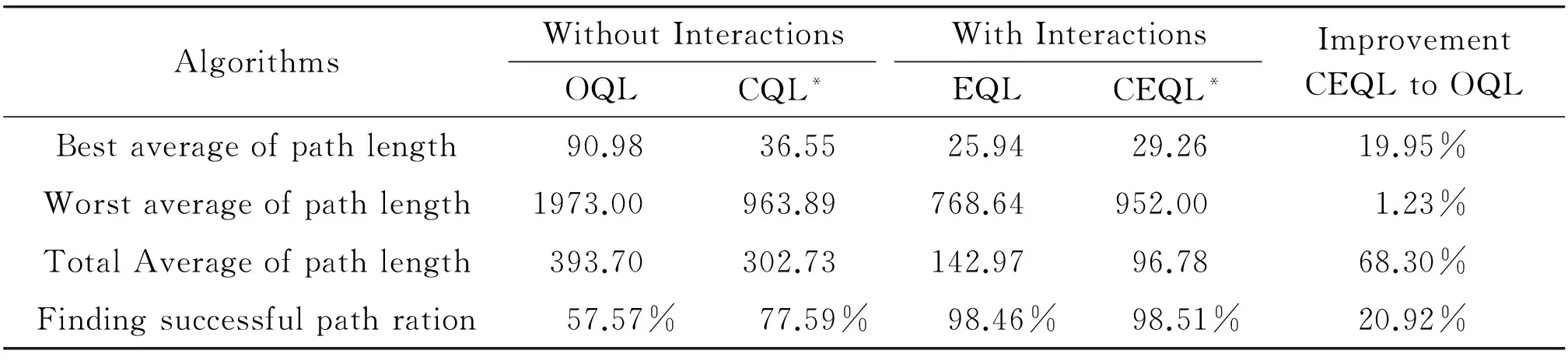
Table 2 Experimental result for dynamic environment.

6 Conclusion

Learning through interacting with environments and other agents is a common problem in the context of multi agent system. Multi task learning allows some related tasks to be simultaneously jointly learned using a joint model. In this scope, learners use the commonality among the tasks. Also reinforcement learning is a type of learning agent concerned with how an agent should take actions in an environment in order to make the most of agents’ reward. RL is a useful approach for an agent to learn its policy in a nondeterministic environment. However, it is considered such a time consuming algorithm that it can’t be employed in every environment.

We found that the existence of interaction between agents is a proper approach for betterment in speed and accuracy of RL methods. To improve the performance of multi task reinforcement learning in a nondeterministic and dynamic environment, especially for dynamic maze problem, we store past experiences of agents. By simulating agents’ interactions by structures and operators of evolutionary algorithms, we explore the best exchange of agents’ experiences. We also switch to a chaotic exploration instead of a random exploration. Applying Dynamic Chaotic Evolutionary Q-Learning Algorithm to an exemplary maze, we reach significantly promising results.

Our examinations have shown about 91.02% improvement in using interactions between agents and applying the best past experiences of agents compared to original RL algorithm without any interactions in terms of average case of found path length. Also it has about 5.09% improvement in using chaotic exploration compared with non-chaotic in average.

This can be inferred from experimental results that employing chaos as random generator in exploration phase as well as evolutionary-based computation can improve the reinforcement learning, in both rate of learning and its accuracy. It can also be concluded that using chaos in exploration phase is efficient for both evolutionary based version and non-evolutionary one.

[1]H.P.Kriegel, P.Kröger, and A.Zimek, Clustering high-dimensional data: a survey on subspace clustering, pattern-based clustering, and correlation clustering,ACMTransactionsonKnowledgeDiscoveryfromData, vol.3, no.1, pp.1-58,2009.

[2]N.H.Park and S.L.Won, Grid-based subspace clustering over data streams, inProceedingsofthesixteenthACMconferenceonConferenceoninformationandknowledgemanagement, Lisbon, Portugal, 2007,pp.801-810.

[3]N.H.Park and S.L.Won Suk, Cell trees: an adaptive synopsis structure for clustering multi-dimensional on-line data streams,Data&KnowledgeEngineering,vol.63,no.2, pp.528-549,2007.

[4]W.Liu and J.OuYang, Clustering algorithm for high dimensional data stream over sliding windows, inProceedingsoftheIEEE10thInternationalConferenceonTrust,SecurityandPrivacyinComputingandCommunications, Paris, France, 2011, pp.1537-1542.

[5]Z.Aoying, Tracking clusters in evolving data streams over sliding windows,KnowledgeandInformationSystems,vol.15,no.2, pp.181-214, 2008.

[6]S.Lühr and M.Lazarescu, Connectivity Based Stream Clustering Using Localised Density Exemplars, inProceedingsof12thPacific-AsiaConferenceonKnowledgeDiscoveryandDataMining, Osaka, Japan, 2008, pp.662-672.

[7]B.Minaei-Bidgoli, H.Parvin, H.Alinejad-Rokny, H.Alizadeh, and W.Punch, Effects of resampling method and adaptation on clustering ensemble efficacy,ArtificialIntelligenceReview, vol.41, no.1, pp.27- 48,2012.

[8]C.Böhm, Computing Clusters of Correlation Connected objects, inProceedingsofthe2004ACMSIGMODinternationalconferenceonManagementofdata, Paris, France, 2004,pp.455-466.

[9]M.Mohammadpour, H.Parvin, and M.Sina, Chaotic Genetic Algorithm based on Explicit Memory with a new Strategy for Updating and Retrieval of Memory in Dynamic Environments,JournalofAIandDataMining, 2017, doi: 10.22044/JADM.2017.957.

[10] D.Arthur and V.Sergei, k-means++: the advantages of careful seeding, inProceedingsoftheeighteenthannualACM-SIAMsymposiumonDiscretealgorithms, New Orleans,USA, 2007, pp.1027-1035.

[11] H.Parvin, B.Minaei-Bidgoli, H.Alinejad-Rokny, and S.Ghatei, An innovative combination of particle swarm optimization, learning automaton and great deluge algorithms for dynamic environments,InternationalJournalofPhysicalSciences, vol.6,no.22, pp.5121-5127,2011.

[12] M.H.Fouladgar, B.Minaei-Bidgoli, H.Parvin, and H.Alinejad-Rokny, Extension in The Case of Arrays in Daikon like Tools,AdvancedEngineeringTechnologyandApplication, vol.2,no.1, pp.5-10,2013.

[13] I.Jamnejad, H.Heidarzadegan, H.Parvin and H.Alinejad-Rokny, Localizing Program Bugs Based on Program Invariant,InternationalJournalofComputingandDigitalSystems, vol.3,no.2, pp.141-150,2014.

[14] B.Prasad, D.C.Dimri, and L.Bora, Effect of pre-harvest foliar spray of calcium and potassium on fruit quality of Pear cv.Pathernakh,ScientificResearchandEssays,vol.10,no.11, pp.392-396,2015.

[15] G.Singh, Optimization of Spectrum Management Issues for Cognitive Radio,JournalofEmergingTechnologiesinWebIntelligence,vol.3,no.4, pp.263-267, 2011.

[16] H.Parvin, H.Alinejad-Rokny, and S.Parvin, A Classifier Ensemble of Binary Classifier Ensembles,InternationalJournalofLearningManagementSystems, vol.1,no.2, pp.37- 47,2013.

[17] D.Madhuri, Linear Fractional Time Minimizing Transportation Problem with Impurities,InformationSciencesLetters,vol.1,no.1, pp.7-19, 2012.

[18] J.Mayevsky, J.Sonn, and E.Barbiro-Michaely, Physiological Mapping of Brain Functions In Vivo: Surface Monitoring of Hemodynamic Metabolic Ionic and Electrical Activities in Real-Time,JournalofNeuroscienceandNeuroengineering,vol.2,no.2, pp.150-177,2013.

[19] H.Parvin, H.A.Rokny, S.Parvin, and H.Shirgahi, A new conditional invariant detection framework (CIDF),ScientificResearchandEssays,vol.8,no.6,pp.265-273,2013.

[20] S.P.Singh and B.K.Konwar, Insilico Proteomics and Genomics Studies on ThyX of Mycobacterium Tuberculosis,JournalofBioinformaticsandIntelligentControl,vol.2,no.1, pp.11-18,2013.

[21] H.Parvin, H.Alinejad-Rokny, B.Minaei-Bidgoli, and S.Parvin, A new classifier ensemble methodology based on subspace learning,JournalofExperimental&TheoreticalArtificialIntelligence, vol.25,no.2,pp.227-250,2013.

[22] M.Kaczmarek, A.Bujnowski, J.Wtorek, and A.Polinski,JournalofMedicalImagingandHealthInformatics,vol.2,no.1, pp.56-63,2012.

[23] M.Zamoum, and M.Kessal, Analysis Of Cavitating Flow Through A Venturi,ScientificResearchandEssays,vol.10,no.11, pp.383-391,2015.

[24] H.Parvin, H.Alinejad-Rokny, and S.Parvin, A New Clustering Ensemble Framework,InternationalJournalofLearningManagementSystems, vol.1,no.1, pp.19-25,2013.

[25] D.Rawtani and Y.K.Agrawal, Study the Interaction of DNA with Halloysite Nanotube-Gold Nanoparticle Based Composite,JournalofBionanoscience, vol.6,no.2,pp.95-98, 2012.

[26] H.Parvin, B.Minaei-Bidgoli, and H.Alinejad-Rokny, A New Imbalanced Learning and Dictions Tree Method for Breast Cancer Diagnosis,JournalofBionanoscience, vol.7,no.6,pp.673- 678,2013.

[27] Z.Chen, F.Wang, and Li Zhu, The Effects of Hypoxia on Uptake of Positively Charged Nanoparticles by Tumor Cells,JournalofBionanoscience,vol.7,no.5, pp.601-605,2013.

[28] J.G.Bruno, Electrophoretic Characterization of DNA Oligonucleotide-PAMAM Dendrimer Covalent and Noncovalent Conjugates,JournalofBionanoscience,vol.9,no.3, pp.203-208,2015.

[29] K.K.Tanaeva, Yu.V.Dobryakova, and V.A.Dubynin, Maternal Behavior: A Novel Experimental Approach and Detailed Statistical Analysis,JournalofNeuroscienceandNeuroengineering,vol.3,no.1, pp.52-61,2014.

[30] M.I.Jamnejad, H.Parvin, H.Alinejad-Rokny, and A.Heidarzadegan, Proposing a New Method Based on Linear Discriminant Analysis to Build a Robust Classifier,JournalofBioinformaticsandIntelligentControl, vol.3,no.3,pp.186-193,2014.

[31] R.Ahirwar, P.Devi, and R.Gupta, Seasonal Incidence Of Major Insect- Pests And Their Biocontrol Agents Of Soybean Crop (Glycine Max L.Merrill),ScientificResearchandEssays, vol.10,no.12, pp.402- 406,2015.

[32] S.Sharma and B.Singh, Field Measurements for Cellular Network Planning,JournalofBioinformaticsandIntelligentControl,vol.2,no.2, pp.112-118,2013.

[33] H.Parvin, M.MirnabiBaboli, and H.Alinejad-Rokny, Proposing a Classifier Ensemble Framework Based on Classifier Selection and Decision Tree,EngineeringApplicationsofArtificialIntelligence, vol.37, pp.34- 42,2015.

[34] M.Kaczmarek, A.Bujnowski, J.Wtorek, and A.Polinski, Journal of Medical Imaging and Health Informatics,vol.2,no.1, pp.56-63,2012.

[35] N.Zare, H.Shameli, and H.Parvin, An innovative natural-derived meta-heuristic optimization method,AppliedIntelligence, doi: 10.1007/s10489-016-0805-z,2016.

[36] D.Rawtani and Y.K.Agrawal, Study the Interaction of DNA with Halloysite Nanotube-Gold Nanoparticle Based Composite,JournalofBionanoscience, vol.6,no.2, pp.95-98,2012.

[37] A.Aminsharifi, D.Irani, S.Pooyesh, H.Parvin, S.Dehghani, K.Yousofi, E.Fazel, and F.Zibaie, Artificial neural network system to predict the postoperative outcome of percutaneous nephrolithotomy,JournalofEndourology, vol.31,no.5, pp.461- 467,2017.

[38] H.Parvin, H.Alinejad-Rokny, N.Seyedaghaee, and S.Parvin, A Heuristic Scalable Classifier Ensemble of Binary Classifier Ensembles,JournalofBioinformaticsandIntelligentControl, vol.1,no.2,pp.163-170,2013.

[39] Z.Chen, F.Wang, and Li Zhu, The Effects of Hypoxia on Uptake of Positively Charged Nanoparticles by Tumor Cells, Journal of Bionanoscience, vol.7,no.5,pp.601- 605,2013.

[40] J.G.Bruno, Electrophoretic Characterization of DNA Oligonucleotide-PAMAM Dendrimer Covalent and Noncovalent Conjugates,JournalofBionanoscience,vol.9,no.3, pp.203-208,2015.

[41] K.K.Tanaeva, Yu.V.Dobryakova, and V.A.Dubynin, Maternal Behavior: A Novel Experimental Approach and Detailed Statistical Analysis,JournalofNeuroscienceandNeuroengineering,vol.3,no.1, pp.52-61,2014.

[42] E.Zaitseva and M.Rusin, Healthcare System Representation and Estimation Based on Viewpoint of Reliability Analysis,JournalofMedicalImagingandHealthInformatics,vol.2,no.1, pp.80-86, 2012.

•Sadrolah Abbasi is with Department of Computer Engineering, Iran Health Insurance Organization, Yasouj, Iran.

•Hamid Parvin, Mohamad Mohamadi, and Eshagh Faraji are with Department of Computer Engineering, Nourabad Mamasani Branch, Islamic Azad University, Nourabad Mamasani, Iran.

•Hamid Parvin and Eshagh Faraji are with Young Researchers and Elite Club, Nourabad Mamasani Branch, Islamic Azad University, Nourabad Mamasani, Iran. E-mail: h.parvin.iust@gmail.com.

*To whom correspondence should be addressed. Manuscript

2017-05-26; accepted: 2017-06-30