分段自适应遗传算法在流水车间调度中的应用

安徽理工大学电气与信息工程 汪 鹏

分段自适应遗传算法在流水车间调度中的应用

安徽理工大学电气与信息工程 汪 鹏

针对流水车间的优化调度问题，提出一种分段自适应遗传算法，对遗传算法交叉、变异算子进行改进，从而有效避免算法陷入局部，达到算法优化调度的目的。通过对标准遗传算法和改进算法进行仿真验证得知，优化后的算法具有更好的适应度曲线，表明其有效的克服了标准遗传算法不成熟收敛问题，具有一定的工程应用价值。

分段自适应；遗传算法；流水车间

0 引言

随着市场竞争的加剧，各制造加工企业为了提高自身的竞争力，必须合理分配资源，提高设备利用率与生产效率，降低生产成本，这就需要制定良好的车间生产调度。为此本文设计一种分段自适应遗传算法，随着进化代数和适应度函数自动调整交叉概率和变异概率，以期以较快的收敛速度搜索到全局最优解，从而满足实际生产应用的需要。

1 问题描述

流水车间调度问题（Flow shop Scheduling Problem, FSSP）是一种最重要的组合优化问题， 该问题通常可以描述为n个工件要在m台不同机器上加工，每个工件有m道工序，每道工序都要在不同的机器上加工，各个工件加工顺序相同，且满足如下的约束条件：1）每个工件在机器上的加工顺序相同，且给定加工顺序是1，2，3…，m；2）一个工件不能同时在不同的机器上进行加工；3）每台机器同时只能够加工一个工件；4）工序的准备时间与顺序无关，且包含在加工时间内；5）工件加工技术上的约束事先给定。

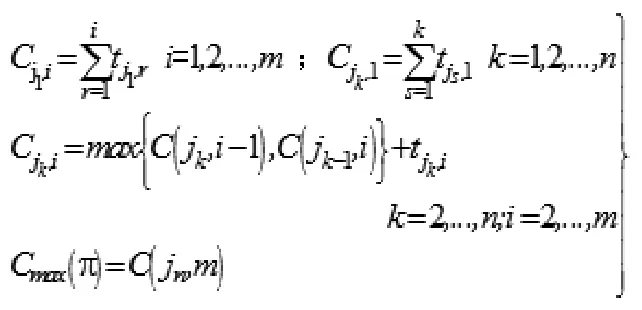
2 问题的算法设计

遗传算法包括三个基本的操作：选择、交叉和变异。遗传算法的交叉概率Pc和变异概率Pm的选择是影响遗传算法行为和性能的关键，直接影响算法的收敛性，Pc的大小决定种群的更新速度和搜索快慢的指标。Pm是保持种群多样性，防止早熟的一种手段。基于以上问题，本文提出了分段自适应遗传算法实时调整交叉概率及变异概率，从而获得较优解。

该算法分四个进化阶段。M为总进化代数，itmax最大迭代代数，iter当前代数，Pcmax最大交叉概率，Pcmin最小交叉概率，Pmmax最大变异概率，Pmmin最小变异概率，f变异个体适应度（目标函数值），fcmax为交叉两个体较大适应度，fave种群平均适应度，fmax种群适应度最大值。分别是1-0.4M代，Pcmax=0.8，Pcmin=0.6，Pmmax=0.08，Pmmin=0.05；0.4M-0.7M代，Pcmax=0.7，Pcmin=0.5，Pcmax=0.06，Pmmin=0.03；0.7M-0.9M代，Pcmax=0.6，Pcmin=0.4，Pmmax=0.04，Pmmin=0.02；0.9M到M代，Pcmax=0.5，Pcmin=0.3，Pmmax=0.02，Pmmin=0.01。

该算法参数设计的数学表达式如下：

其中，α和β为随机产生的权重系数。

3 车间调度问题仿真及结果分析

为了验证算法的有效性，本文分别将标准遗传算法和分段自适应遗传算法的性能应用于不同规模的流水车间调度问题，算法均用MATLAB2012a来实现，并在Pentium3.2Ghz×2GB内存的机器上的加工时间使用著名的Taillard’s基准算例。

图1

如图1所示，采用ta011(20×10)算例仿真，最优值为1582，明显看出分段自适应遗传算法优于标准遗传算法，具有较好的寻优能力，从而验证了算法的优越性。

4 结论

本文研究了流水车间调度问题，提出了性能较优的分段自适应遗传算法，仿真结果表明，该算法在处理流水车间问题更能优化目标函数，取得更好的效果。

[1]王凌．车间调度及其遗传算法[M]．北京:清华大学出版社,2003．

[2]张博凡,黄宗南．基于变形遗传算法交叉算子的Flow-Shop问题求解[J]．制造业自动化,2011(19):27-29,46．

[3]Taillard,E．Benchmarks for basic scheduling problems．European Journal of Operational Research[J]．1993,64:278-285．