基于极点配置的双馈风力发电机并网系统的静态稳定性分析

杨春华，章 艳，周 玮，孙 辉

(1.国家电网宜昌供电公司，湖北 宜昌 443000；2.大连理工大学电气工程学院，辽宁 大连 116024)

基于极点配置的双馈风力发电机并网系统的静态稳定性分析

杨春华1，章 艳2，周 玮2，孙 辉2

(1.国家电网宜昌供电公司，湖北 宜昌 443000；2.大连理工大学电气工程学院，辽宁 大连 116024)

为研究双馈风力发电机的运行特点及并网时系统的静态稳定性，基于双馈风力发电机电压、磁链方程，考虑不同传动轴系对风机运行的影响，推导建立单台风电机组两质量块动态模型。结合小信号分析法，对风机所在系统进行静态稳定性分析。在不同控制模式下，存在稳定与不稳定运行情况，通过极点配置法，在不完全可控的情况下令系统的稳定性得到明显改善。

双馈风力发电机；两质量块；可控性；极点配置法；静态稳定性

0 引言

大容量的风电场接入电力系统后，由于双馈风电机组自身的闭环控制，不能像同步机那样及时响应外界的变化，从而降低了电力系统抗干扰能力。风电机组并网下的静态稳定性分析是近年来的研究热点[1-5]。基于李雅普诺夫线性化的小干扰稳定性特征值分析法是常用的分析方法[6-10]。为更好地进行定性研究，许多学者从不同侧重面对风力发电机进行了动态建模，其中文献[11-12]将双馈风力发电机等效为绕线式异步电机；文献[13-14]从风电机组的电气特性出发，对于直驱式永磁风机和双馈式感应电机进行了详细介绍。然而风电机组是一个机械与电磁同时存在的复杂模型，单一考虑电气特性忽略轴系机械传动影响也不全面。文献[15-17]强调风机轴系模型的建立，指出多质量块模型对风机系统稳定性讨论的重要性。单质量块模型将机械驱动简化为一部分，用于粗略分析。三质量块模型需要将齿轮箱的惯性分摊到高速轴和低速轴，适用于精度要求高的场合。文献[18]提出了一种新型无功电压控制策略，实现无功电压控制，增强了系统稳定性。若需要改善系统的静态稳定性，基于同步发电机在励磁调节部分加入电力系统稳定器，文献[19]在双馈风力发电机控制部分增加阻尼控制器。附加阻尼控制方法在改善稳定性方面效果也十分显著[20]。

本文以双馈风力发电机为主要讨论对象，考虑轴向传动模型，基于单台双馈风力发电机的两质量块有功-频率动态方程；并根据系统特征值的分布情况判断系统的静态稳定性，特别是在系统不稳定情况下，采用现代控制原理，讨论系统的可控性，将系统分解使之满足极点配置法的使用条件，通过增加状态反馈改善系统稳定性。

1 两质量块的双馈风力发电机并网模型

1.1双馈风力发电机电磁特性

双馈风力发电机主要由风力机、传动的齿轮箱、绕线式异步发电机、网侧变频器和机侧变频器构成。通过最大风能捕获将风能转化成电能，两个变流器的作用使机侧到网侧的功率双向流动。

图1 变流器的控制结构图Fig.1 Control structure of converter

dq0旋转坐标系中，基本方程式可归纳如下：

式中：p为微分算子；下标s代表定子，r代表转子；ls为定子自电感；lr为转子自电感；lm为定转子之间的互感；Rs和Rr分别为定子和转子电阻；s为转差率，s=1-ω，ω为转子角速度。

根据式(1)、(2)可得电压电流方程：

(3)

1.2双馈风力发电机两质量块机械传动轴系模型

考虑轴系扭振和机械传动轴系的影响，采用两质量块模型描述风力机与发电机的机械部分：

(4)

式中：Hw、Hg分别为等效风力机和发电机转子(含齿轮箱(若有))质量块的标么值惯性常数；ωw、ωg分别为风力机和双馈风力发电机的角速度；θb为轴系扭转角；khg、Dw分别为轴系刚度系数和等效风力机自身阻尼系数；Dg、Dhg为等效发电机自身阻尼系数；Tw、Te分别为风力机机械转矩和双馈风力发电机电磁转矩。

1.3变流器控制模型

采用矢量定向控制，假设定子磁链与旋转坐标系的d轴重合，有

(5)

忽略定子电阻，即Rs=0，则有

(6)

在dq0坐标系下，控制器采用PI控制，变频器的控制框图如图1所示。

1.4双馈风力发电机并网状态方程

为分析双馈风力发电机的静态稳定性，依据小扰动稳定性分析的建模方法，线性化上述方程为

(7)

式中：Δx是状态变量；A、B为11阶系数矩阵。其中：Δx=[ΔωwΔωgΔθbΔψds Δψqs Δidr Δiqr Δx1Δx2Δx3Δx4]T，Δx1、Δx2、Δx3、Δx4是变流器控制环节中间变量[21]；Kp=[0 0 0 0

lmuqs0/ls0 -uqs0/ls0 0 0 0]。

根据线性化理论系统可求得

GPω(s)=Kp(sI-A)-1B

(8)

式中:s为拉普拉斯算子；I为单位阵。从而获得单台双馈风力发电机传递函数的表达式。

2 不同控制下系统静态稳定性比较

双馈风力发电机并网时变流器控制部分采用双闭环控制策略，功率控制环和电流控制环均采用PI控制器。根据系统状态方程(8)可求得系统特征值。选择单台双馈风力发电机的容量为1.5 MW，系统参数如下：Rr=0.005 pu，Rs=0.0071 pu，lm=2.9 pu，ls=3.071 pu，lr=3.056 pu，Hw=4.54，Hg=0.5，khg=0.3，Dw=2，Dhg=1，Dg=1。对于单机无穷大系统，变流器PI控制参数不同时，系统会出现稳定运行情况和不稳定运行情况。选择一组稳定运行情况定义为模式1，在不稳定运行情况下，选择两组不稳定情况定义为模式2和模式3，便于下文中不稳定模式下极点配置前后对比。不同模式下系统特征值结果如表1所示。对应的PI控制参数如下：

1)模式1。kp=kq=0.001，kpi=kqi=0.5，cp=cq=0.003，cpi=cqi=0.003。

2)模式2。kp=kq=0.01，kpi=kqi=0.5，cp=cq=0.03，cpi=cqi=0.003。

3)模式3。kp=kq=0.1，kpi=kqi=0.5，cp=cq=0.3，cpi=cqi=0.003。

其中：kp和kq分别表示有功、无功比例调节参数；kpi和kqi分别表示有功、无功积分调节参数；cp和cq表示电流控制环调节增益；cpi和cqi表示电流控制环积分调节参数。

通过表1可看出，变流器PI控制参数直接影响系统静态稳定性。模式1所有的特征根都在复平面的左半平面，系统稳定。模式2、3出现了正根(表中加粗部分)，系统不稳定。模式1分别在阶跃、脉冲信号激励下观察双馈风力发电机并网系统稳态响应，如图2所示。在初始系统稳定的情况下，小干扰激励信号作用于该系统，经过一段调整时间的调整，最后系统恢复到原有的稳定状态。

3 系统不稳定模式下的可控性分析

闭环系统的特征值反映的是系统的稳定性能，在状态空间方法的分析和综合中，大多采用极点配置的方法，利用状态反馈或是输出反馈配置极点，提供抗干扰性或鲁棒性等更多的校正信息，抑制或消除扰动影响。本文采用极点配置法调整不稳定情况下的极点位置。

根据上文所述，存在不稳定的情况，希望通过控制的手段改善该系统的静态稳定性。控制作用能否对系统的所有状态变量产生影响，先需要讨论该系统的可控性。

3.1系统状态可控性判断

满足式(7)的状态空间表达式，可将状态可控性的代数判据归纳为：系统能控性矩阵的秩为满秩时，系统可控。即有

3.2特征根PBH秩判据

对于不可控的系统，根据PBH秩判据可以看出每个特征根对整体可控性的影响。具体做法如下，系统完全能控的充要条件是对于系数阵A的所有特征值λi(i=1,2,…,n)，rank[λiI-A,B]=n,i=1,2,…,n。

针对本文系统，计算结果如下：

1)系统输入状态方程的能控性矩阵rank(Q)=10<11，系统状态不可控。

表1 不同模式下系统特征根Table 1 System characteristic root under different patterns

图2 模式1的稳态响应Fig. 2 Steady state response of mode 1

2)系统输出状态方程的能控性矩阵rank(Q′)=1，因为Kp维数为1×11。所以输出可控。

3.3系统分解后的极点配置

将上述系统分解成可控部分和不可控部分，后续调节可控部分，改变其静态稳定性。对于线性定常被控系统：

(9)

根据自动控制原理，选择合适的非奇异变换矩阵P。

式(9)变换为以下的表达式：

将式(10)、(11)展开就能得到可控和不可控的

两个子系统。针对含有不稳定特征值的可控子系统，选取线性反馈控制律为

u=v-Kx

(12)

式中K为线性反馈控制器。构成图3所示的闭环反馈控制系统。

图3 闭环反馈控制系统Fig.3 Closed loop feedback control system

线性定常系统可通过线性状态反馈任意地配置其全部极点的充要条件是：此被控系统状态完全可控。分解以后的可控子系统和不可控子系统的状态变量为

不稳定状态变量完全可控，可以进行极点配置。首先计算出分解后可控子系统的状态空间表达式，按图3的控制框图代入数据。通过线性状态反馈控制，模式2、3不稳定情况下配置前后的极点如表2所示。在采用极点配置法之前，两种模式下均存在不稳定的特征值，经过极点配置以后系统所有的特征值均在复平面的左半轴。

表2给出了模式2、3在极点配置之前和极点配置以后的特征根分布，系统由之前的不稳定到配置后稳定。从图4的(a)、(b)与(c)、(d)对比可看出，在单位阶跃和单位冲击信号作用下，不稳定的系统在极点配置以后趋于稳定。

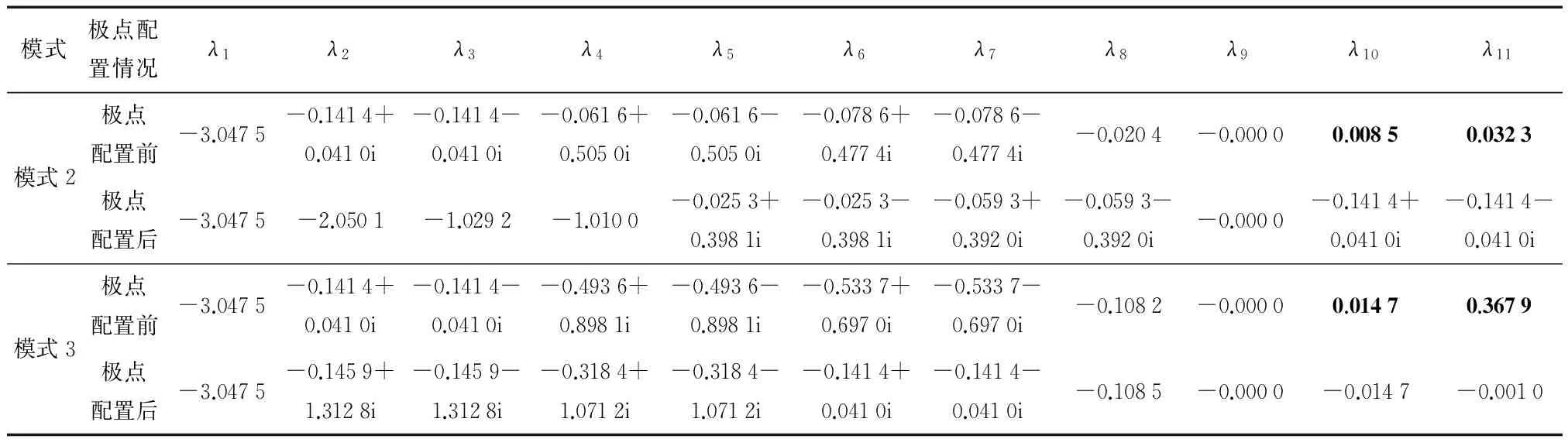
表2 极点配置前后特征值比较Table 2 Comparison of eigenvalues before and after pole placement

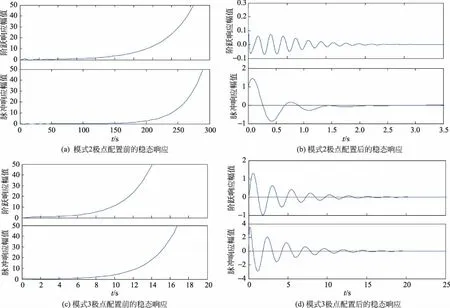
图4 模式2、3极点配置前后对比图Fig.4 Comparison of mode 2,3 before and after pole placement

4 结论

综上所述，采用本文的建模方法，在原有的电压磁链方程基础上，考虑到了机械传动的影响，采用两质量块模型建模更接近风电机组本身的结构特性。可通过极点配置法改善可控系统的静态稳定性。当不稳定系统处于不完全可控的情况下，系统经过分解以后，对可控子系统部分可以直接进行极点配置，系统抗扰能力增强，从而提高了双馈风电机组并网的静态稳定性。

[1] CHAI C I, LEE W J , FUANGFOO P, et al. System impact study for the interconnection of wind generation and utility system[J]. IEEE Transactions on Industry Applications, 2005, 41(1): 163-168.

[2] 吴涛， 于啸， 郭嘉阳， 等. 暂态稳定计算中双馈型风电机组模型与参数的实证分析[J]. 电网技术， 2011, 35(1)： 100-105. WU Tao, YU Xiao, GUO Jiayang, et al. Empirical analysis on model and parameters of grid-connected doubly fed induction generators in transient stability computation[J]. Power System Technology， 2011， 35(1): 100-105.

[3] ULLAH N R, THIRINGER T. Variable speed wind turbines for power system stability enhancement[J] IEEE Transaction on Energy Conversion, 2007, 22(1): 52-60.

[4] 和萍， 文福拴， 薛禹胜， 等. 不同类型风电机组对小干扰和暂态稳定性的影响[J]. 电力系统自动化， 2013， 37(17): 23-29. HE Ping, WEN Fushuan, XUE Yusheng, et al. Impacts of different wind power generators on power system small signal and transient stability[J]. Automation of Electric Power Systems， 2013， 37(17): 23-29.

[5] BU S Q, DU W, WANG H F, et al. Probabilistic analysis of small-signal stability of large-scale power systems as affected by penetration of wind generation[J]. IEEE Transactions on Power Systems, 2012, 27(2): 762-770.

[6] 王忱， 石立宝， 姚良忠， 等. 大规模双馈型风电场的小扰动稳定分析[J]. 中国电机工程学报， 2010， 30(4): 63-70. WANG Chen, SHI Libao, YAO Liangzhong, et al. Small signal stability analysis of the large-scale wind farm with DFIGs[J]. Proceedings of the CSEE， 2010， 30(4): 66-70.

[7] MISHRA Y, MISHRA S. LI Fangxing, et al. Small-signal stability analysis of a DFIG-based wind power system under different modes of operation[J]. IEEE Transactions on Energy conversion, 2009, 24(4): 972-982.

[9] 汤宏， 吴俊玲， 周双喜. 包含风电场电力系统的小干扰稳定分析建模和仿真[J]. 电网技术， 2004， 28(1): 38-41. TANG Hong， WU Junling， ZHOU Shuangxi. Modeling and simulation for small signal stability analysis of power system containing wind farm[J]. Power System Technology， 2004， 28(1): 38-41. [10] 颉迪， 卢占会， 李庚银， 等. 一类含异步风电机组的电力系统小干扰区间稳定性分析[J]. 中国电机工程学报， 2015， 35(3): 609-614. XIE Di, LU Zhanhui, LI Gengyin, et al. Interval stability analysis of small signal for a class of power system with asynchronous wind turbine generators[J]. Proceedings of the CSEE， 2015， 35(3): 609-614.

[11] 高景德， 王祥珩， 李发海. 交流电机及其系统的分析[M]. 2版. 北京： 清华大学出版社， 2005： 383-398.

[12] 李晶， 宋家葬， 王伟胜. 大型变速恒频风力发电机组建模与仿真[J]. 中国电机工程学报， 2004， 24(6): 100-105. LI Jing, SONG Jiazang， WANG Weisheng. Modeling and dynamics simulation of variable speed wind turbine with large capacity[J]. Proceedings of the CSEE， 2004， 24(6): 100-105.

[13] 冯双磊， 赵海翔， 任普春， 等. 基于PSCAD/EMTDC的双馈式变速恒频风电机组动态模型仿真[J]. 电网技术， 2007， 31(17): 30-35. FENG Shuanglei, ZHAO Haixiang, REN Puchun, et al. PSCAD/EMTDC based simulation study on dynamic model of doubly-fed variable speed wind turbine[J]. Power System Technology. 2007, 31(17): 30-35.

[14] MULLER S, DEICKE M, DE DONCKER R W. Doubly fed induction generator systems for wind turbines[J]. IEEE Industry Applications Magazine, 2002, 8(3): 26-33.

[15] 刘胜永， 张兴， 谢震， 等. 风力发电系统机械传动机构动态模型研究[J]. 太阳能学报， 2011， 32(8): 1258-1263. LIU Shengyong, ZHANG Xing, XIE Zhen, et al. A study on dynamic model of mechanical transmission in wind power generation system[J]. Acta Energiae Solaris Sinica, 2011, 32(8): 1258-1263.

[16] 李东东， 陈陈. 风力发电机组动态模型研究[J]. 中国电机工程学报， 2005， 25(3): 115-119. LI Dongdong， CHEN Chen. A study on dynamic model of wind turbine genrator sets[J]. Proceedings of the CSEE， 2005， 25(3): 115-119.

[17] 解大， 冯俊淇， 娄宇成， 等. 基于三质量块模型的双馈风机小信号建模和模态分析[J]. 中国电机工程学报， 2013， 33(增): 21-29.

XIE Da, FENG Junqi, LOU Yucheng, et al. Small-signal modelling and modal analysis of DFIG-based wind turbine based on three-mass shaft model[J]. Proceedings of the CSEE， 2013， 33(Supplement): 21-29.

[18] 盛四清, 陈安. 双馈风电场新型无功电压控制策略研究[J]. 分布式能源, 2017, 2(2): 39-43. SHENG Siqing, CHEN An. A new strategy of reactive power and voltage control for DFIG in wind farm[J]. Distributed Energy, 2017, 2(2): 39-43.

[19] 赵书强， 常鲜戎， 贺仁睦， 等. PSS控制过程中的借阻尼现象与负阻尼效应[J]. 中国电机工程学报. 2004, 24(5): 7-11. ZHAO Shuqiang， CHANG Xianrong， HE Renmu, et al. Borrow damping phenomena and negative damping effect of PSS control[J]. Proceedings of the CSEE， 2004， 24(5): 7-11．

[20] 李辉， 陈耀君， 赵斌， 等. 双馈风电场抑制系统次同步振荡分析及控制策略[J]. 中国电机工程学报, 2015, 35(7): 1613-1620. LI Hui, CHEN Yaojun, ZHAO Bin, et al. Sub-synchronous oscillation analysis and control strategy for doubly-fed wind farm suppression system[J]. Proceedings of the CSEE, 2015, 35(7): 1613-1620.

[21] 郝正航. 双馈风电机组的暂态行为及其对电力系统稳定性影响[D]. 天津： 天津大学, 2011. HAO Zhenghang. Transient behavior of doubly-fed wind turbine and its influence on power system stability[D]. Tianjin： Tianjin University, 2011.

杨春华

(编辑 谷子)

StaticStabilityAnalysisofDouble-FedWindGeneratorGrid-ConnectedSystemBasedonPoleAssignment

YANG Chunhua1, ZHANG Yan2, ZHOU Wei2, SUN Hui2

(1. State Grid Yichang Power Supply Company, Yichang 443600, Hubei Province, China;
2. School of Electric Engineering, Dalian University of Technology, Dalian 116024, Liaoning Province, China)

To study the operating characteristics of doubly-fed wind generator and the static stability of the connected grid, this paper considers the influence of different drive shafts on the operation of wind turbine based on the voltage of doubly-fed wind generator and flux linkage equations, derives the dynamic model of the two mass block of single unit. By combining the small signal analysis method, this paper analyzes the static stability of the wind turbine system. Under different control modes, there are stable and unstable running conditions; and the stability of the system is significantly improved by the pole assignment method in the case of incomplete control.

doubly-fed wind generator; two mass block; controllability; pole assignment method; static stability

TK 89;TM 71

： A

： 2096-2185(2017)04-0059-06

10.16513/j.cnki.10-1427/tk.2017.04.010

2017-04-05

杨春华(1990—)，男，硕士，助理工程师，研究方向为电力系统分析与控制，dut_ychh@163.com；

章 艳(1980—)，女，博士研究生，研究方向为风机系统稳态运行；

周 玮(1981—)，女，博士，讲师，研究方向为电力系统优化运行与大电网经济化调度；

孙 辉(1964—)，女，教授，博士生导师，研究方向为电力系统分析与控制。