对一个征解题的探究

魏国祥，李凤清，张子卫

（四川职业技术学院应用数学与经济系，四川 遂宁 629000）

对一个征解题的探究

魏国祥，李凤清，张子卫

（四川职业技术学院应用数学与经济系，四川 遂宁 629000）

本文对《数学通讯》上半月刊2015年第3期问题征解栏目第206号问题进行了探究，得出了它的一个推广：已知a,b,c,m为正实数且满足a b c=1同时得出几个有用的相关结论，最后提出了一个猜想：已知a,b,c,λ,m 为正实数且满足 a b c=1，λ≥1，（1+m a）（1+m b）（1+m c）.

数学问题；不等式；推广；猜想

《数学通讯》上半月刊2015年第3期问题征解栏目第206号问题为：

已知为a,b,c正实数且满足a b c=1，求证：

我们对问题进行探究，得到下面一些结论.

从定理1的证明中可得下面结论.

结论1已知a,b,c,m为正实数且满足a b c=1，则（1+m a）（1+m b）（1+m c）.

结论2已知a,b,c,λ,m为正实数且满足a b c=1，λ≥1，则

（1+aλ）（1+bλ）（1+cλ）≥（1+a）（1+b）（1+c）.

证明（1+aλ）（1+bλ）（1+cλ）≥（1+a）（1+b）（1+c）等价 于（aλ+bλ+cλ）+[（a b）λ+（b c）λ+（c a）λ] ≥（a+b+c）+（a b+b c+c a）.

由幂平均不等式可知

同理可知，（a b）λ+（b c）λ+（c a）λ≥a b+b c+c a

故（aλ+bλ+cλ）+[（a b）λ+（b c）λ+（c a）λ]≥（a+b+c）+（a b+b c+c a），故结论2成立.

推论 已知a,b,c,λ 为正实数且满足a b c=1，λ≥2，则

（1+aλ）（1+bλ）（1+cλ）≥（1+a2）（1+b2）（1+c2）.

由这个推论与结论1可得下面结论.

结论 3已知 a,b,c,λ,m为正实数且满足a b c=1，λ≥2则

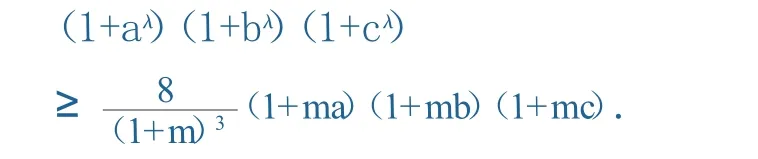
结论 4已知 a,b,c,λ,m为正实数且满足a b c=1，m≥5，λ≥1，则

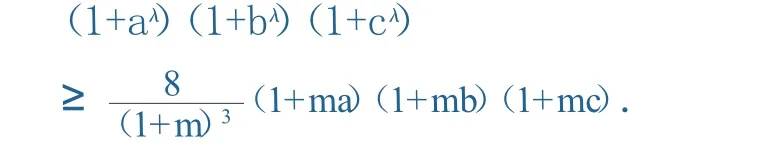
证明 由 结 论 2 可 知 （1+aλ）（1+bλ）（1+cλ）≥（1+a）（1+b）（1+c），故只需证（1+a）（1+b）（1+c）≥（a+b+c）+[（1+m）3-8 m] （a b+b c+c a） ≥8 （m3+1）-2（1+m）3.若 m≥5，可知（1+m）3-8 m2＞0，（1+m）3-8 m2＞0与 4（m3+1）-（1+m）3≥0 均成立. 由于 a+b+c≥3，a b+b c+c a≥3故

[（1+m）3-8 m]（a+b+c）+[（1+m）3-8 m2]（a b+b c+c a）≥3[2（1+m）3-8 m2-8 m]=6 m3-6 m2-6 m+6

可知结论4成立.

下面提出一个猜想.

猜想已知a,b,c,λ,m为正实数且满足a b c=1，λ≥1，则

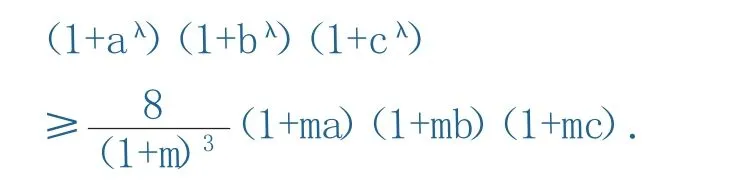
[1]佚名.第206号问题//问题征解[J]数学通讯（上半月刊），2015，（3）.

责任编辑：张隆辉

O 122

A

1672-2094（2017）04-0165-02

2017-05-08

魏国祥（1971-），男，四川遂宁人，四川职业技术学院讲师。研究方向：数学教育。