论数学分析教学中的师范特色

蒋红瑛

（四川职业技术学院应用数学与经济系，四川 遂宁 629000）

论数学分析教学中的师范特色

蒋红瑛

（四川职业技术学院应用数学与经济系，四川 遂宁 629000）

分析师范数学教育与中学数学教育的现状,揭示师范数学教育中数学分析和中学数学之间的联系，对数学分析中的师范特色进行论述。

中学数学;高等师范;师范特色;数学分析;数学思想方法

高等师范教育的培养目标是为中学提供能适应当今新课程标准要求的合格教师，而高等师范数学专业培养的学生大多是未来的中学数学教师，因此高等师范数学教育应为数学专业学生今后所从事的教师职业给予充分的培养，努力提高数学教育的综合能力,这也正是高等师范数学教育区别于其它高校数学教育的一个基本特点——师范性。

长期以来,高等师范数学教育并没有充分体现师范性特点。究其主要原因，其一是高等师范数学课程的教学与中学数学严重脱节，教师不注重引导学生用所学的高等数学知识去理解和指导中学数学；其二是大多数大学教师只把自己当作一个科研人员，而不是一个教师，因此他们在教学过程中只管知识的讲解，忽视教学法的合理运用，结果使得学生没有得到很好的教学法的培养。

而数学分析是师范数学专业最重要的基础课程之一，内容多、学时长，其内容经典、体系完善、理论严谨、应用广泛，不仅是数学系学生首先面临的一门重要课程，而且大学理科本科乃至研究生阶段很多后续课程在本质上都可视为它的延伸、深化或应用，它的基本概念、基本理论、数学思想、数学方法对中学数学中的函数、极限、方程、面积、体积等具有实效性的指导作用，这充分说明了数学分析在中学数学中的重要性。因此，怎样在数学分析课程教学中体现师范特色呢？结合自己的教学实践总结为以下几点。

1 注意教学内容安排的循序渐进

如今，全国各地的高等院校均在进行课程改革的探索，数学分析是数学系最重要的核心必修课程之一，内容多、学时长、难度大、晦涩难懂。因此，教学安排上必须着墨于“循序渐进”。即第一学年把课程主体内容讲授完毕，淡化难点和证明，主要强调计算能力和对微积分的历史认识和应用前景认识；第二学年加强训练，强调证明的逻辑严谨性，锻炼学生严格推理能力，使之具备严格的书写数学证明的能力。

2 观注教学方法的探索

教学方法是教师和学生为了实现共同的教学目标，完成共同的教学任务，在教学过程中运用的方式和手段的总称。而教学方法的选择因教学内容而异，因人而异。由于数学分析的内容较多，所以在教学中采用的教学方法也应多样化，但必须恰当合理地运用。比如，连续性概念、极限概念、微分概念等的讲解主要采用讲授法，而且尽量将数学语言“通俗化”，让学生容易理解和接受。比如“连续性概念”，可先给出“植物的连续生长”，“人的年龄连续增长”，“春、夏、秋、冬的连续变化”等生活中熟习的例子，让学生得以连续的印象，感知数学就在我们身边，不再抽象，从而对这摸不着的数学知识产生兴趣；函数内容在中学学习过，因此主要用自学辅导法，让学生在学习过程有成就感；在学习了一元微积分知识的基础上，对二元微积分以及多元微积分的教学可运用建构类比法；在微分中值定理的教学中，对于辅助函数的构造运用发现式和启发式教学法等等.

3 重视数学思想方法的教学

数学分析是在初等数学的基础上，经过一系列数学概念、原理和方法的演变而发展起来的一门高度抽象、逻辑严密的学科体系，所以数学分析不仅继承了初等数学的方法，如函数思想、化归思想、数形结合思想以及数学建模思想，还引进了新的思想方法——极限方法。

极限方法是数学分析的主线和基础，也是数学分析解决问题的基本方法，它与初等数学方法的本质区别在于极限方法体现了辩证思想。因为极限概念的ε-δ和ε-N定义形式中的具有二重性，即确定性和任意性。所以建立在极限思想方法基础上的数学分析可以揭示和把握常量和变量、直线和曲线、匀速运动和变速运动等的对立统一及矛盾相互转化关系，这也正是初等数学思想方法不能办到的。若能灵活地借助极限思想解题，往往可以避免复杂运算，优化解题过程，降低解题难度。例如已知0＜x＜y＜a＜1,则有( )

所以在教学中必须加强对极限思想方法和其反映出来的辩证关系的讲授，让学生能站在哲学的高度来学习这一门课的知识，理解这一门课的深刻内涵。当然也不能忽视其他一些常用的思想方法和讲解，如通过中值定理的证明介绍数形结合和构造的数学思想方法；通过定积分的计算或等式证明来介绍变换思想；通过洛比达法则求极限来介绍化归思想等等。

4 加强数学分析对初等数学的指导作用

我们知道，初等数学是研究常量的数学，而数学分析是在实践中为了解决初等数学不能解决的问题而长期逐步发展起来的变量数学。数学分析不仅使我们居高临下地去观察初等问题，以确定解题思路，有时它还能帮助我们剖析某些问题的实质。相反地，某些初等问题正是借助于高等数学的思想去拟造的。所以数学分析的原理和方法对理解初等数学的知识和解决初等数学问题起着指导作用。比如：利用极限方法来建立几何中的面积与体积公式；利用导数和微分来证明三角恒等和不等式问题；用初等函数的一阶导函数的连续性来解释为什么初等函数图象是光滑曲线；利用幂级数来定义初等数学中的三角函数和指数函数等，还可利用幂级数理论来讲授怎样构造中学所运用的常用对数表和三角函数表；利用定积分来给出柱体、锥体、台体和球体的体积公式以及证明立体几何中的恒等原理，也可利用定积分来证明不等式问题。

例如(2012年全国数学联赛题)已知n为正整数，

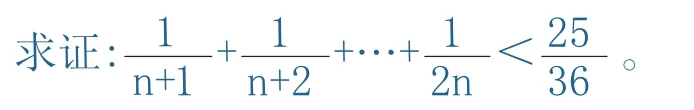
分析：这是一边为常数另一边与自然数有关的不等式，标准答案是用数学归纳法证明比这个不等式更强的不等式这个不等式是怎么来的令人费解。若由所证式子联想到在用定积分求曲边梯形面积的过程中“分割求和”这一步，则可考虑用定积分的几何意义求解.。在（0，+∞）上是凹函数，由函数图象可知，在区间[n,2 n]上的n个矩形的面积之和小于曲边梯形的面积，

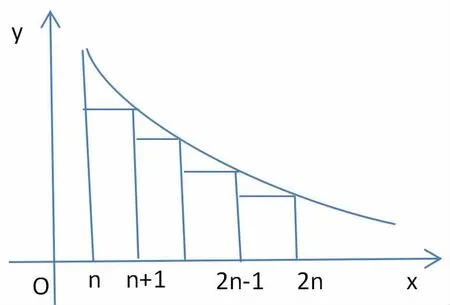
证明：构造函数

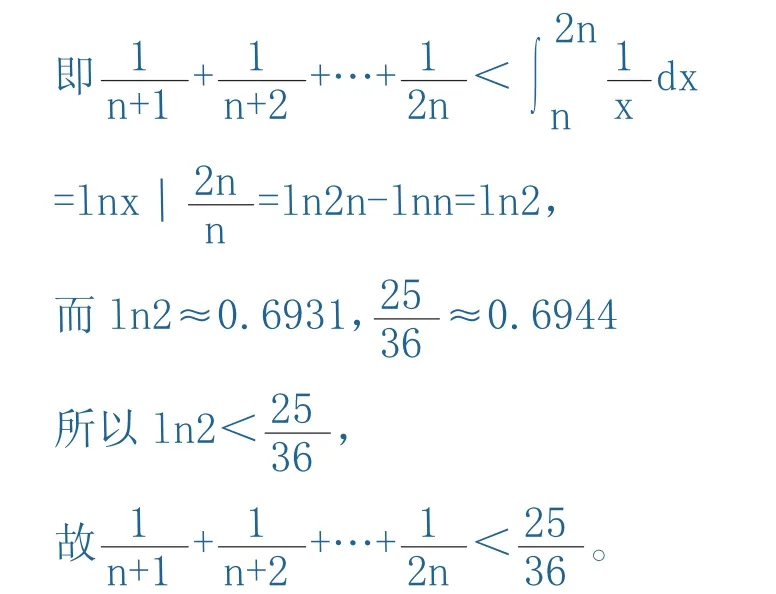
数学分析教学中，一定要注重数学分析与初等数学的联系和结合，以真正发挥高等数学对初等数学的指导作用，使学生能用高观点理解中学新课标下数学教材，提高学生解决初等数学问题的能力，为他们今后当好中学数学教师打下坚实基础。

5 注重数学史的介绍

每一门学科都有一个萌芽、发生与发展的历史，数学分析也不例外。历史上，数学分析起源于17世纪，伴随牛顿和莱布尼兹创立微积分开始，并发展到函数的连续性、可微分及可积分等各种特性，它的每一步进步都经历了漫长的过程和倾注了无数数学家的心血。因此，在教学过程中，加上数学史的介绍，不仅是让学生了解数学分析的发展史，更重要的是通过历史的数学的研究和学习，可引起学生对数学的兴趣，培养学生不甘落后、勇于进取、敢于创新的创造性心理品格，激励学生立志于数学教育和数学研究。例如讲级数时，首先介绍著名的悖论之一——阿基里斯与龟，让学生从心底里产生急于明白问题的渴望，认真听取老师的讲解，待课堂内容和计算方法给出后，让学生自己找出阿基里斯一定能追上乌龟的原因，从而否定追不上的结论。这样不仅让学生掌握了级数的收敛与发散，体会到极限学习的重要性，同时还享受到自己破解了前人难题的喜悦，提高了学习的兴趣和积极性。

6 注重美学思想在教学中的渗透

“哪里有数学，哪里就有美!”——古希腊数学家普洛克拉斯。

数学中存在着美，但这种美不同于其他形式的美，而是与数学本身的特点联系在一起的。那什么是数学美呢?数学大师罗素曾直言不讳的说：“数学，如果正确地看它，不但拥有真理，而且也具有至高无上的美，正像雕刻的美，是一种冷而严肃的美!”它的存在形式为统一美、奇异美、抽象美和简洁美。特别地，数学分析作为一门数学专业的基础课，处处充满了美的情趣，美的创造，美的表现和美的享受。一些函数图象所表现出来的对称和谐美；一些题型解题过程的简洁美；还有一些题型解题方法的巧妙性所带给人的奇异美等等。例如在讲授泰勒公式时，让学生深切感知数学的奇异美和统一美：各种完全不同的函数f（x），只要它们在包含x0的区间(a,b)内有n+1阶导数，都可统一成如下形式，即x∈(a,b)，有

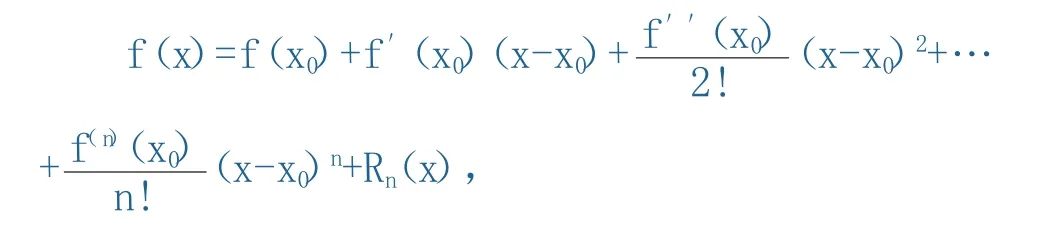
挖掘数学美，传授数学美，是高校课改背景下的教师必须具备的教学技能，是学生对数学产生兴趣的源泉。因此,在数学分析教学中，把美学渗透到理论知识的学习中，与知识的传授同步进行，从而达到提高学生审美的力，培养学生创造美的能力。

[1]徐伟华.数学分析教学方法的认识与探讨[J].中国科教创新导刊，2011，（01）．

[2]唐永．应用极限思想解题[J]．中学数学，2005，（06）．

[3]谭超强.浅谈数学分析课程教学改革[J].汕头大学学报（自然科学版），2014，（03）．

[4]成宝娟.数学分析课程对中学数学的指导作用[J].佳木斯教育学院学报，2013，（02）．

On the Characteristics of Teachers in Mathematical Analysis Teaching

JIANG Hongying

(Sichuan Vocational and Technical College, Suining Sichuan 629000)

This paper analyzes the present situation of mathematics education in normal school and middle school, reveals the relation between mathematical analysis and middle school mathematics in normal mathematics education, and expounds the characteristics of normal mathematics in the course of mathematics analysis.

Middle School Mathematics; Higher Normal; Teacher Characteristics; Mathematical Analysis; Mathematical Thinking Method

G 642

A

1672-2094（2017）04-0104-03

责任编辑：张隆辉

2017-06-06

蒋红瑛（1971-），女，四川遂宁人，四川职业技术学院副教授。研究方向：数学教育。