基于花授粉算法的曲面薄壁件定位布局优化
王仲奇 李 诚 杨 勃 杨 元
西北工业大学现代设计与集成制造技术教育部重点实验室,西安,710072
基于花授粉算法的曲面薄壁件定位布局优化
王仲奇 李 诚 杨 勃 杨 元
西北工业大学现代设计与集成制造技术教育部重点实验室,西安,710072
优化定位布局是减小薄壁件装夹变形的重要手段,现有研究大多以节点法向变形最小为优化目标而忽略其他方向上的变形,为此提出了一种新的基于花授粉算法的夹具布局优化方法。针对曲面薄壁件,在建立法向约束定位模型的基础上,通过应变能来描述所有方向上的变形,以薄壁件的整体应变能最小为目标,结合花授粉算法和基于Python语言的参数化有限元分析,实现薄壁件的定位布局寻优。最后以飞机蒙皮定位布局优化为例验证方法的有效性,并通过与遗传算法的对比表明,花授粉算法在优化薄壁件的定位布局时具有更优的性能。
薄壁件;定位布局优化;应变能;花授粉算法
0 引言
薄壁件具有质量轻、强度高和几何造型流畅等优点。广泛采用低密度与高强度的薄壁结构件是飞机制造过程的必然趋势,然而典型薄壁结构件多为大尺寸、弱刚性件,在仅受重力的情况下就会产生不可忽视的变形。装夹是影响薄壁件变形的重要因素,不合理的装夹方案会造成变形超差从而影响装配质量,严重的情况下甚至导致工件报废[1]。设计合理的装夹方案,对减小变形保障装配精度具有重要意义。CAI等[2]首次提出了针对弱刚性薄板零件的“N-2-1”定位原理,在主定位面上采用N(N>3)个定位元件,以过定位的方式来限制变形,然而N的大小与位置如何确定,还没有完善的求解理论和方法。
传统定位方案的设计依赖于主观经验判断来针对工件弱刚度部位进行加强,经验设计依赖于个人水平,设计随意性大,难以满足越来越高的装配精度要求。为此,许多学者围绕薄壁件定位布局优化问题展开了研究。采用有限元分析来计算变形,采用遗传算法等智能优化算法进行给定数目下位置的优化,是当前求解定位布局优化问题的主要方法。PADMANABAN等[3]以蚁群算法为基础,通过最小化薄壁件的弹性变形,对加工过程中的夹具布局进行优化。姜潮等[4]针对焊装夹具的定位点优化问题,利用有限元方法计算主定位面上的变形,采用全局收敛性强的隔代映射遗传算法来寻找最优布局。吴铁军等[5]以定位误差最小为优化目标,基于模糊评价法来确立定位点数目,并应用遗传算法对定位点的位置进行优化。石志云等[6]基于遗传算法利用APDL语言提出了定位点优化布置方法,研究了重力作用下定位点的分布。CHENG等[7]针对航空薄壁件自动钻铆过程,建立了分级的定位布局优化模型,并结合遗传算法和蚁群算法对定位点位置进行了优化。张恒等[8]提出了一种基于惯性权值的粒子群改进算法,并将该优化算法应用于夹具定位点的优化设计。于金等[9]以平均变形量最小为目标,基于遗传算法对铣削加工中的装夹位置进行了优化。周涛等[10]结合有限元分析与蚁群遗传混合算法进行了支承阵列的布局优化,使薄壁件的最大变形量缩小47%。王仲奇等[11]以薄壁件自重引起的最大变形量最小为目标,采用萤火虫算法实现了定位布局的迭代寻优。
然而,上述研究大多以最小化薄壁件法向变形为目标,忽略其他方向的变形,而曲面薄壁件的变形并非集中在法向方向。为此,本文提出了一种新的基于花授粉算法的定位布局优化方法。针对曲面薄壁件,通过应变能来衡量所有方向上的变形,结合花授粉算法和有限元分析进行薄壁件定位布局寻优,并以飞机蒙皮的定位布局优化为例验证所提方法的有效性。
1 问题描述
对于一般刚性件,装配过程需使用夹具进行定位以保持其稳定性与位置确定性,而对于弱刚性的薄壁件而言,还需适当增加定位件的数目来校正形状与限制变形。薄壁件的“N-2-1”定位原理如图1所示,即在主定位面上使用N(N>3)个定位元件进行定位,而在第二和第三基准面上分别使用2个和1个定位元件。装夹过程中,在夹紧力与支承力的作用点处会产生装夹应力,由于薄壁件的刚性较差,夹、压的弹性变形会影响工件表面的尺寸精度和位置精度,作用点的位置和数目不同,所产生的弹性变形也就不同,严重情况下就会造成变形超差,因此,优化定位元件布局,包括其数目与位置,是减小装夹变形的重要手段。
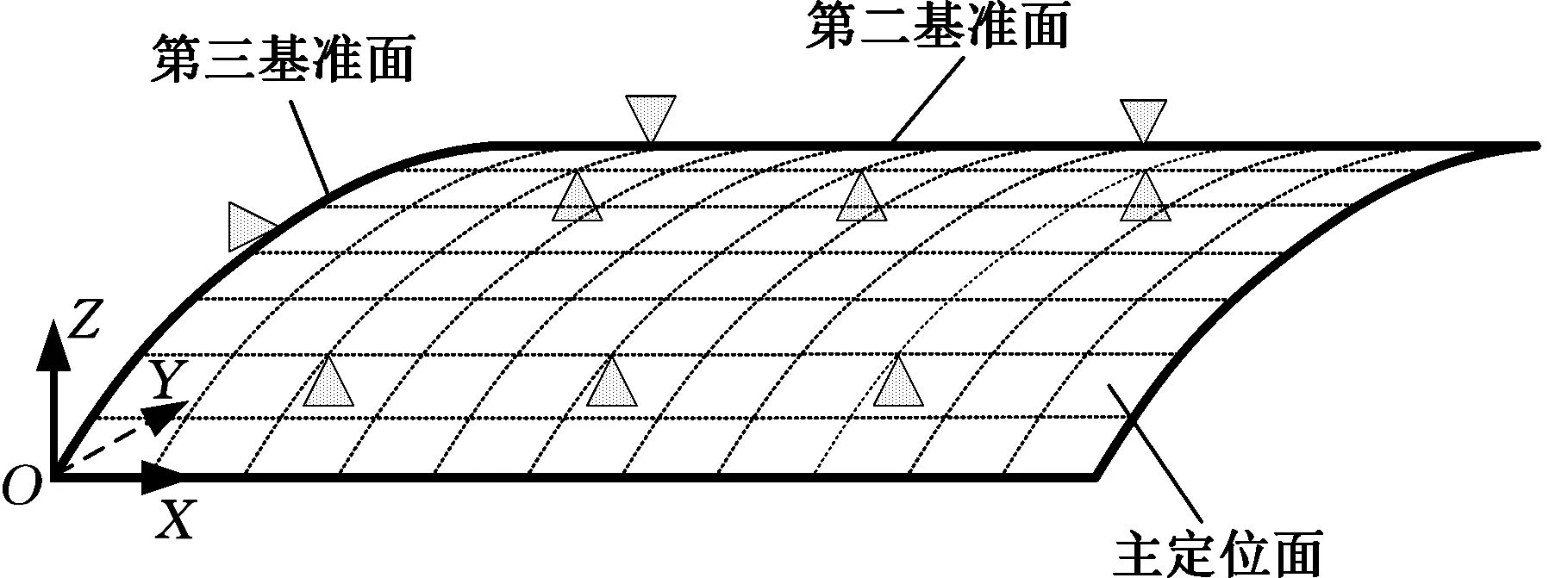
图1 薄壁件“N-2-1”定位原理Fig.1 “N-2-1” locating principle for thin-walled part
在主定位面上,定位元件的数目N一般大于3,理论上,N值越大变形越小,但N的取值并非越大越好。定位元件增多必然造成时间和成本增加,定位元件的制造偏差和装夹过程中的定位偏差对变形的影响也更加复杂,反而会降低精度,因此,薄壁件的定位布局优化问题即是确定满足装配精度要求的尽可能小的N值,并在确定N的数目后优化N的位置使得薄壁件的变形最小。
2 曲面法向约束定位理论
制造业中广泛运用NURBS曲面来描述薄壁件的表面形状。一张以(u,v)为参变量的k×l阶NURBS曲面可定义为
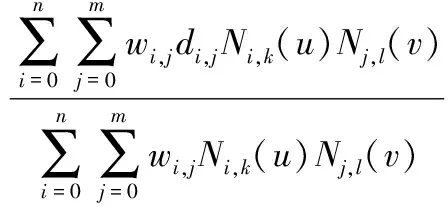
(1)
其中,di,j(i=0,1,…,m;j=0,1,…,n)为空间中给定的m×n个控制顶点;wi,j为与顶点di,j对应的权因子;Ni,k(u)、Nj,l(v)分别是u向k次和v向l次的规范B样条基。
薄壁件定位过程中,定位元件对薄壁件施加法向约束力,方向沿着接触点处的法向指向被支撑的薄壁件,以约束薄壁件沿着这一方向的位移。对于平板件而言,任意点的法向均垂直于主定位面,因此在N个定位点处施加垂直于主定位面的约束以抑制该方向的变形即可。而对于曲面件而言,定位元件相切于薄壁件支承面,通过点接触来定位,如图2所示,约束方向沿着各自局部坐标系(LCS)下接触点的法向。
薄壁件受到重力和重力矩的作用(称为重力旋量,用Wg表示)以及沿着法向的支撑力Fni(i=1,2,…,m)的作用。受力平衡方程为
(2)
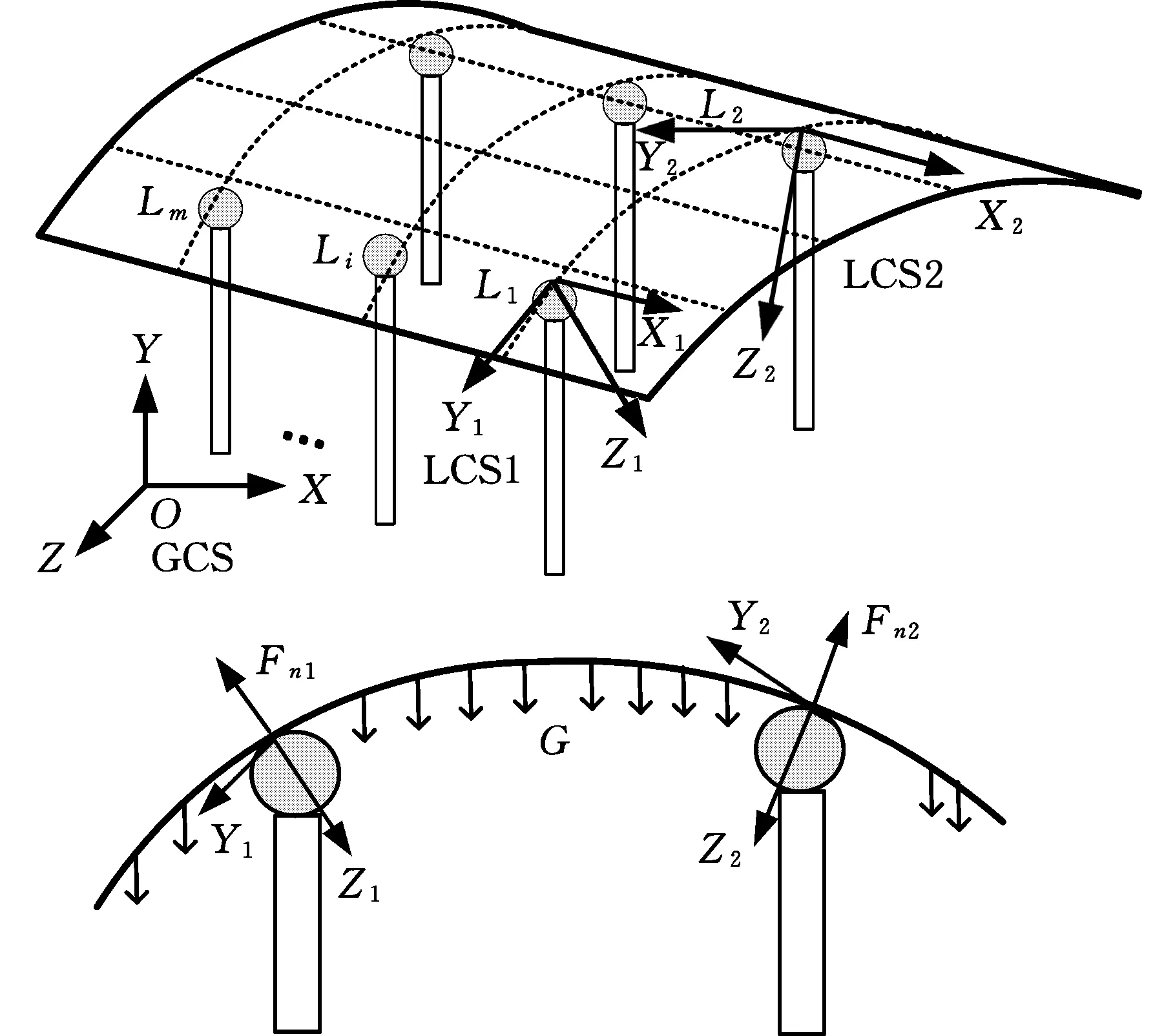
图2 法向约束定位模型Fig.2 Locating model under normal constraint
其中,L=(L1,L2,…,Lm)表示定位元件的布局矩阵,rc=(rc1,rc2,…,rcm)T为m个定位元件在全局坐标系(GCS)下的位置向量。n=(n1,n2,…,nm)为各定位元件的单位法矢量,NURBS曲面上任意点(us,vt)处的单位法矢量n(us,vt)可参照文献[12-13] 计算。Fn=(Fn1,Fn2,…,Fnm)T表示各定位接触点处的法向支撑力。由式(2)可知,不同的定位布局会导致法向支撑力不同,所产生的弹性变形也就不同。
3 定位布局优化模型
3.1弹性应变能
弹性应变能是指薄壁件由于发生弹性变形而存储的能量,又叫变形能。对于一个三维线弹性体,可被认为由许多小立方体单元组成,在受到载荷F的作用下产生了弹性变形D,单元体内部产生应力如图3所示。
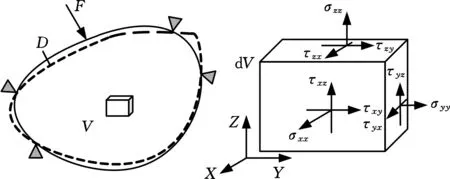
图3 线弹性体应变能Fig.3 Strain energy of linear elastic body
将应力和应变写成向量的形式:
(3)
那么总应变能可以简写为
(4)
不同的定位布局下,薄壁件受到重力和其他装配载荷的作用将产生不同的变形,且全部以应变能的形式存储于薄壁件内。
3.2基于应变能的布局优化模型
定位布局优化问题可被描述为寻找最佳的定位点数目与位置使薄壁件的变形最小。而薄壁件的变形与应变能成正比,可用整体应变能来衡量变形,整体应变能越小意味着变形越小,因此最小化薄壁件变形可转化为最小化整体应变能。以主定位面上的M个定位点的位置X=(x1,x2,…,xM)为设计变量,定位布局优化问题可以用如下方程式描述:
(5)
其中,Ui表示每个有限单元的应变能,K为有限元模型中单元的个数,f(X)是目标函数,表示每种布局X下有限元模型中K个单元的整体应变能。约束条件为每个定位点都必须在允许的有效范围Ω内,不同定位点xi与xj的位置不能重合。
4 基于花授粉算法的定位布局寻优
4.1花授粉算法
受自然界花朵授粉过程的启发,剑桥大学YANG[14]在2012 年提出一种新的元启发式群智能优化算法——花授粉算法(FPA)。该算法模拟自然界中花朵授粉现象,具有调节参数少、寻优能力强、实现简单等优点。其中异花授粉是花粉携带者通过莱维飞行进行的全局授粉,自花授粉被认为是局部授粉。花授粉算法通过转换概率P来控制局部搜索和全局搜索之间的动态平衡,由于受物理邻近性的影响,P值更偏向局部授粉。研究表明[15],相对于遗传算法,花授粉算法有着更好的性能。该算法应用于薄壁件定位布局优化的伪代码如下所示:
定义目标函数f(X)与转移概率P∈[0,1]
X=(x1,x2, …,xM)为M个定位点位置
初始化n组布局方案Xi(i=1,2,…,n)
寻找初始方案中的当前最优值g*
while (t<最大迭代次数)
fori=1∶n
ifrand>P
取一个遵守莱维飞行的步长矢量L
else
取一个[0,1]之间服从均匀分布的γ
在所有花粉配子中随机选择j和k
end if
评价新的布局方案,并接受其中较好的方案
end for
end while
4.2布局优化策略
采用花授粉算法与有限元分析相结合的方法,在MATLAB环境下以花授粉算法为优化主程序,利用有限元软件ABAQUS数值模拟计算应变能,通过求解优化变量X=(x1,x2,…,xM)确定最优布局,从而实现对薄壁件应变能即其变形的控制。优化过程的主要步骤如下:
(1)初始化布局。以3作为主定位面定位点数目N的初值,依次递增,按工程经验均匀布置,并进行有限元分析。取薄壁件最大变形小于工程要求0.5 mm的最少数目作为N值,在可行域内随机生成此N值下的初始位置。
(2)参数化建模。基于Python语言对ABAQUS软件进行二次开发[16],建立参数化有限元模型与后处理过程,以便不断更改定位点位置,进行大量循环迭代计算,提高分析效率。
(3)联合调用计算。通过MATLAB将花粉信息即定位点位置写入Python脚本文件中,以批处理命令调用ABAQUS进行有限元分析,然后读取结果文件并将适应度值赋予相应的花粉配子。
(4)迭代寻优。评价初始花粉配子的适应度值,寻找最优个体,并通过花授粉算法进行位置更新,重复步骤(3)产生新的解。如果新的解较好,则接受新的解,如此循环迭代,直至获得全局最优布局。
上述基于花授粉算法的定位布局优化流程如图4所示。
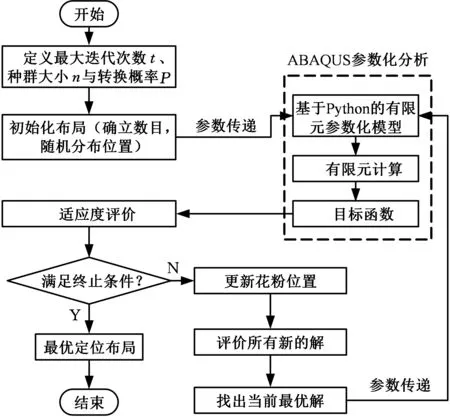
图4 基于花授粉算法的定位布局优化流程Fig.4 Process of fixture locating layout optimization based on FPA
5 实例分析
5.1有限元模型
U=(0,0,0,0,1,1,1,1)V=(0,0,1,1)
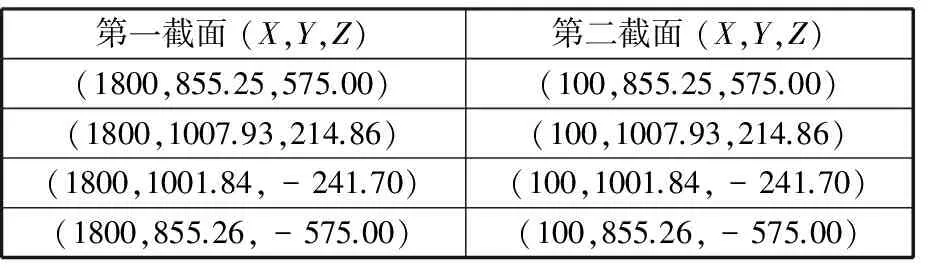
表1 曲面控制点坐标
在三维建模软件CATIA中对飞机蒙皮曲面件进行建模,然后导入ABAQUS 软件进行有限元分析。蒙皮材料为铝合金7075,密度为2.8×103kg/m3,弹性模量为71.2 GPa,泊松比为0.33。蒙皮整体轮廓尺寸为1700 mm×1150 mm,厚度为3 mm。由三次NURBS表示的圆弧作为截面线扫掠而成。两端截面线共含8个控制点,其控制点坐标如表1所示,节点矢量为蒙皮模型共划分为240 000个单元,单元类型为壳单元C3D8R。在主定位面上通过定位点L1~L8进行定位,在建立各定位点局部坐标系的基础上施加法向位移约束。第二基准面通过定位点L9、L10施加两个Z向位移约束,第三基准面通过定位点L11施加一个X向位移约束,蒙皮所受载荷为沿着Y轴反方向的竖直向下的重力。蒙皮定位的有限元模型如图5所示。
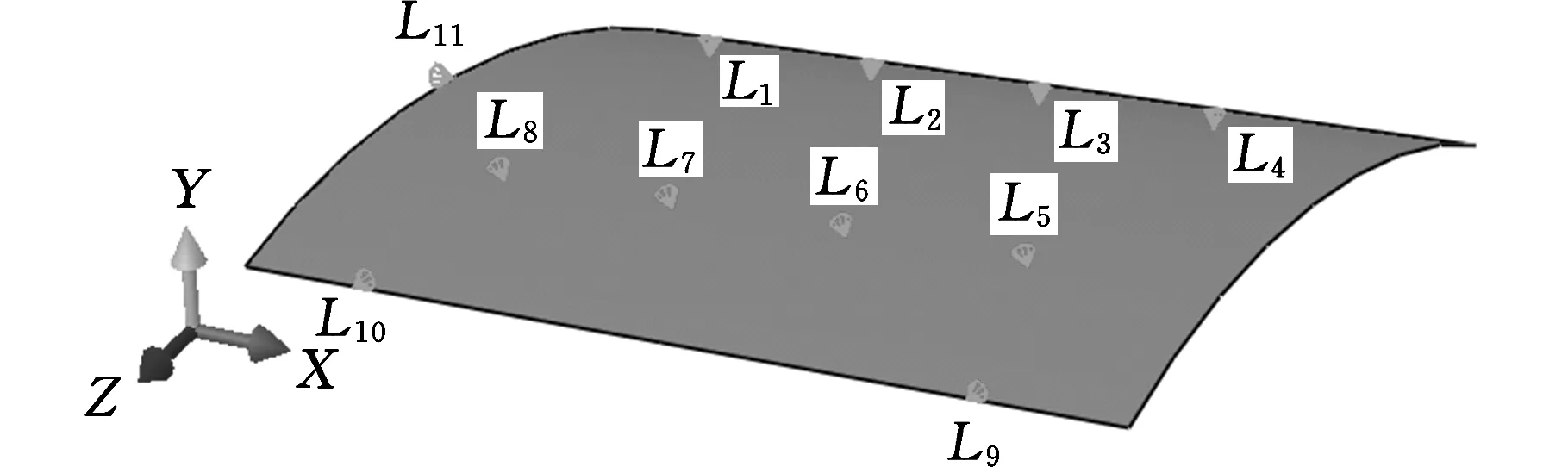
图5 蒙皮定位有限元模型Fig.5 Finite element model of skin locating
5.2优化计算
为了确定N的大小,以3作为N的初值,依次递增,根据工程经验均匀布局,以求得满足最大变形不超过工程要求0.5 mm的最小N值。为了减小经验带来的随机性的影响,每一数目下使用拉丁超立方抽样[17]生成20组均匀布局方案,取20组方案中最优的一组作为该数目下的最大变形值,其结果如图6所示。由图6可知,当N为8时,最大变形值即可满足变形精度要求。在确立了定位点的数目后,对该数目下的定位点位置进一步优化以获取最优定位布局。
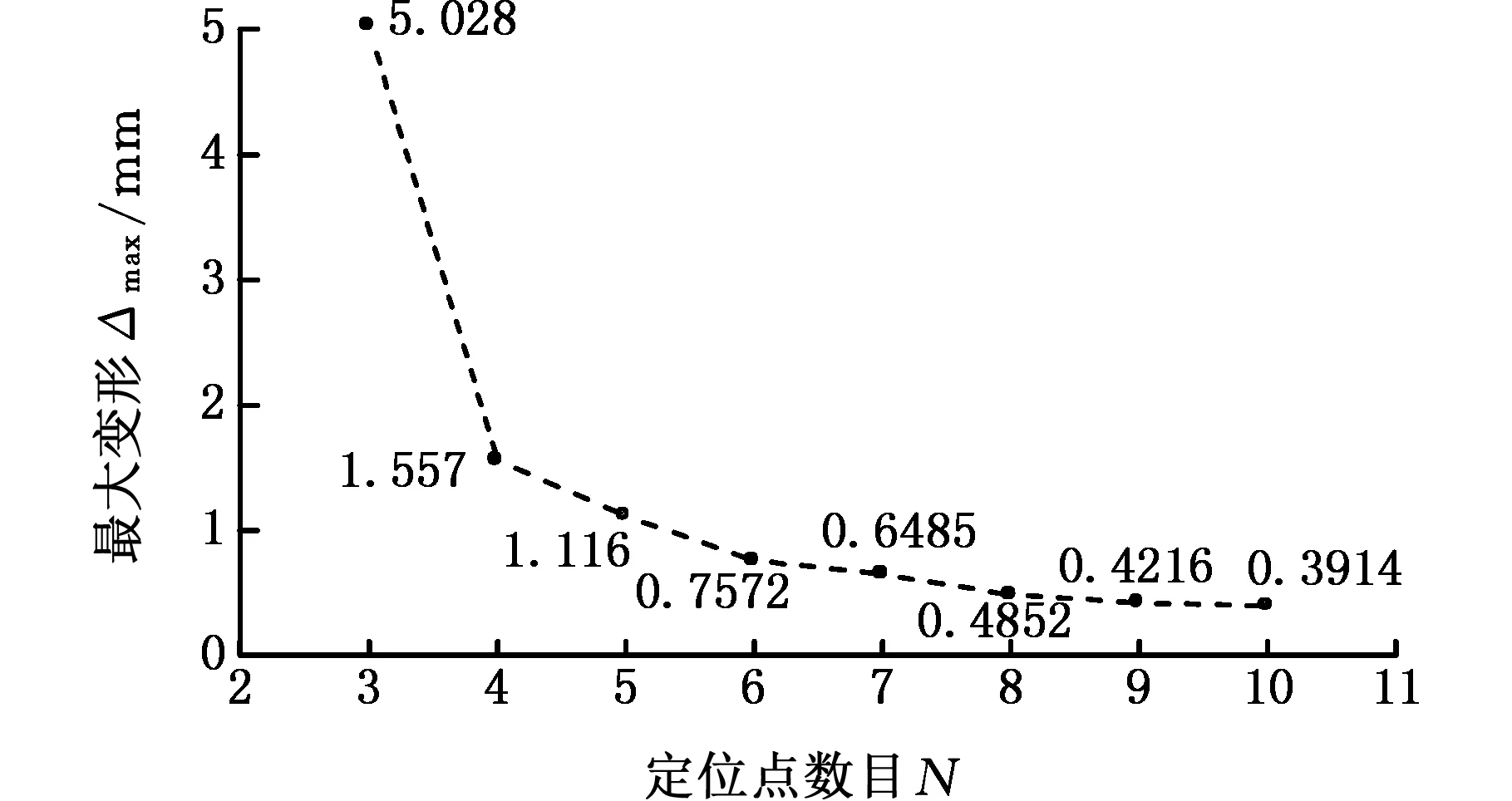
图6 不同N值下的最大变形Fig.6 The maximum deformation with different number of N
为了进一步评估花授粉算法用于定位布局寻优的性能,在相同的初始定位布局与种群大小下,使用遗传算法进行对比寻优。经过若干次试算,取花授粉算法转换概率P=0.7,遗传算法交叉概率Pc=0.7,变异概率Pm=0.02,种群大小为20,最大迭代次数均为200。以主定位面上8个定位点的位置为设计变量,以蒙皮的整体应变能最小为优化目标,分别使用花授粉算法和遗传算法进行定位布局寻优。寻优计算平台如下:操作系统为64位Windows 7,CPU为Intel Xeon X5680,主频3.33 GHz,内存32 GB。优化算法在MATLAB R2013a中运行,有限元分析软件使用ABAQUS 6.12-3。经过全局范围的迭代寻优,定位布局优化结果如表2所示。最小整体应变能和平均整体应变能收敛曲线分别如图7和图8所示。
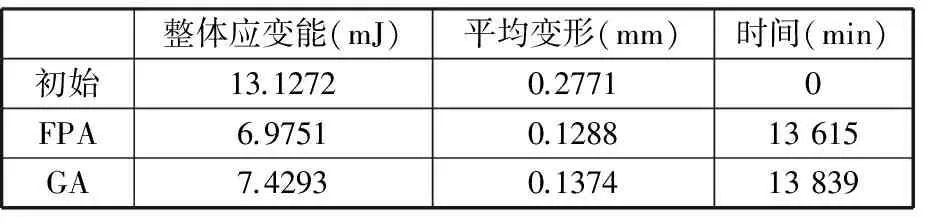
表2 寻优结果对比
使用花授粉算法寻优后,相较于初始布局下蒙皮的整体应变能13.1272 mJ,最优布局下蒙皮的整体应变能为6.9751 mJ,减小了46.87%。进一步对比对所有节点的平均变形,其值减小了53.53%。最优布局下定位点对应的节点编号为(93 257, 223 343,219 592,181 191,195 357,22 950,66 098,81 081)。优化定位布局后蒙皮的整体应变能大大减小,即弹性变形减小,同时平均变形也大幅度降低,表明花授粉算法可有效解决曲面薄壁件的定位布局优化问题。
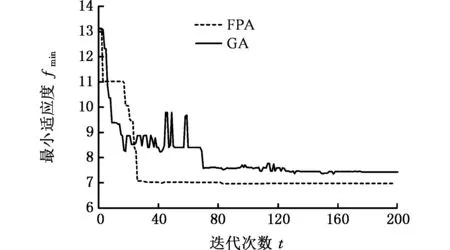
图7 最小适应度收敛曲线Fig.7 The convergence curves of minimum fitness values

图8 平均适应度收敛曲线Fig.8 The convergence curves of average fitness values
此外,由图7可知,对于FPA,当迭代次数约为25代时,曲线即进入了收敛状态,收敛平稳,表明花授粉算法具有较快的收敛速度,且与GA相比能寻找到整体应变能更小的定位布局方案。在图8所示的迭代寻优过程中,FPA的平均适应度值更小,波动更少,意味着FPA比GA具有更好的稳定性和鲁棒性。由上可知,FPA算法可提供更精确和更稳定的结果,收敛速度也优于GA。因此,在薄壁件定位元件的布局优化设计中,FPA算法的整体性能优于GA。
6 结论
(1)通过求解NURBS曲面一点的法向,建立了法向约束下的曲面薄壁件定位模型,提高了模型准确度。
(2)应变能可反映薄壁件所有方向上的弹性变形,更适合作为曲面薄壁件定位布局优化问题的目标函数。
(3)结合有限元分析与花授粉算法有效地求解了自重作用下曲面薄壁件的定位布局优化问题,优化结果满足工程要求。本文方法可进一步应用于制孔力、铆接力等复杂装配载荷下的定位布局优化问题。
[1] 姚荣庆. 薄壁零件的加工方法[J]. 机床与液压, 2007, 35(8):250-253. YAO Rongqing. Research on Processing Technology of Thin-wall Parts [J]. Machine Tool & Hydraulics, 2007, 35(8): 250-253.
[2] CAI W, HU S J, YUAN J X. Deformable Sheet Metal Fixturing: Principles, Algorithms, and Simulations[J]. ASME Journal of Manufacturing Science and Engineering, 1996,118: 318-324.
[3] PADMANABAN K P, ARULSHRI K P, PRABHAKARAN G. Machining Fixture Layout Design Using Ant Colony Algorithm Based Continuous Optimization Method [J]. International Journal of Advanced Manufacturing Technology, 2009, 45(9/10): 922-934.
[4] 姜潮, 韩旭, 钟志华. 电阻点焊焊装夹具定位点的优化设计[J]. 机械工程学报, 2009, 45(4):192-196. Jiang Chao, HAN Xu, ZHONG Zhihua. Locator Optimization for Resistance-spot-welding Fixtures[J]. Journal of Mechanical Engineering, 2009, 45(4): 192-196.
[5] 吴铁军, 楼佩煌, 秦国华. 基于遗传算法的定位布局优化新方法[J]. 南京航空航天大学学报, 2011, 28(2):176-182. WU Tiejun, LOU Peihuang, QIN Guohua. Novel Approach to Locator Layout Optimization Based on Genetic Algorithm [J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2011, 28(2):176-182.
[6] 石志云, 刘渝, 余时建. 基于遗传算法的柔性薄板冲压件定位位置优化设计[J]. 机械科学与技术, 2012(7):1145-1149. SHI Zhiyun, LIU Yu, YU Shijian. The Locators’ Layout Optimization for Flexible Sheet Metal Workpiece Using the Genetic Algorithm[J]. Mechanical Science & Technology for Aerospace Engineering, 2012, 31(7):1145-1149.
[7] CHENG H, LI Y, ZHANG K F, et al. Optimization Method of Fixture Layout for Aeronautical Thin-walled Structures with Automated Riveting[J]. Assembly Automation, 2012, 32(4):323-332.
[8] 张恒, 邢彦锋. 基于改进粒子群算法的薄板件定位策略优化[J]. 河北科技大学学报, 2015, 36(3):300-305. ZHANG Heng, XING Yanfeng. Optimization of Sheet Components Locating Scheme Based on Improved Particle Swarm Optimization[J]. Journal of Hebei University of Science & Technology, 2015, 36(3):300-305.
[9] 于金, 朱秀峰, 高彦梁. 基于遗传算法的接头类薄壁件装夹布局优化设计[J]. 机床与液压, 2015, 43(5):112-114. YU Jin, ZHU Xiufeng, GAO Yanliang. Analysis for Optimal Clamping Scheme of Joint Thin-walled Parts Based on Genetic Algorithm[J]. Machine Tool & Hydraulics, 2015, 43(5):112-114.
[10] 周涛,熊珍琦,姚为,等. 基于改进蚁群算法的薄壁件柔性工装布局优化[J]. 推进技术, 2016, 37(6):1165-1174. ZHOU Tao, XIONG Zhenqi, YAO Wei, et al. Flexible Tooling Layout Optimization for Thin-walled Workpieces Based on Improved ant Colony Algorithm[J]. Journal of Propulsion Technology, 2016, 37(6):1165-1174.
[11] 王仲奇, 黄杰, 康永刚,等. 基于萤火虫算法飞机弱刚性件装配定位策略优化[J]. 机械科学与技术, 2016, 35(4):626-629. WANG Zhongqi, HUANG Jie, KANG Yonggang, et al. Locating Strategy Optimization of Aircraft Weakly Rigid Parts Assembly Based on Firefly Algorithm[J]. Mechanical Science & Technology for Aerospace Engineering, 2016, 35(4):626-629.
[12] 徐志刚, 黄克正, 艾兴. NURBS 曲面法矢量的理论探讨[J]. 机械科学与技术, 1998(5):695-697. XU Zhigang, HUANG Kezheng, AI Xing. Theoretical Discussion on Normal Vector of NURBSSsurface[J]. Mechanical Science & Technology for Aerospace Engineering, 1998(5):695-697.
[13] 莫蓉, 常智勇. 计算机辅助几何造型技术[M]. 北京:科学出版社, 2009. MO Rong, CHANG Zhiyong. Computer-aided Geometric Modeling Technology[M]. Beijing: Science Press,2009.
[14] YANG X S. Flower Pollination Algorithm for Global Optimization[J]. Lecture Notes in Computer Science, 2012, 7445:240-249.
[15] JAGATHEESAN K, ANAND B, SAMANTA S, et al. Application of Flower Pollination Algorithm in Load Frequency Control of Multi-area Interconnected Power System with Nonlinearity[J]. Neural Computing & Applications, 2016, In-press:1-14.
[16] 曹金凤. Python语言在Abaqus中的应用[M]. 北京:机械工业出版社, 2011. CAO Jinfeng. The Application of Python Language in Abaqus[M]. Beijing: Mechanical Industry Press,2011.
[17] STEIN M. Large Sample Properties of Simulations Using Latin Hypercube Sampling[J]. Technometrics, 1987, 29(2):143-151.
(编辑郭伟)
FixtureLocatingLayoutOptimizationofCurvedThin-walledPartsBasedonFDA
WANG Zhongqi LI Cheng YANG Bo YANG Yuan
The Key Laboratory of Contemporary Design and Integrated Manufacturing Technology,Northwestern Polytechnical University,Xi’an,710072
Optimizing the fixture layout of the locating elements was an important means to reduce clamping deformations of thin-walled parts. The normal deformations were taken as the optimization objective in most of the previous studies, while the deformations in other directions were ignored. Based on FPA, a new method used to optimize the fixture locating layouts was proposed herein. At first, the locating model under normal constraints for curved thin-walled parts was established, the deformations in all directions were described by the strain energy. Then, this method, aimed at minimizing the overall strain energy of curved thin-walled parts, combined FPA and parametric finite element analysis based on Python language to realize the optimization of fixture locating layouts. Finally, the effectiveness of the proposed method was validated by the aircraft skin locating layout optimizations, and the comparison results with genetic algorithm(GA) show that the FPA outperforms the GA in terms of the convergence speed and robustness in the thin-walled part fixture locating layout optimization.
thin-walled part; fixture locating layout optimization; strain energy; flower pollination algorithm(FPA)
2016-10-18
陕西省科技统筹创新工程计划资助项目(2016KTCQ01-50);陕西省自然科学基金资助项目(2016JM5011)
TH164;V262.4
10.3969/j.issn.1004-132X.2017.18.013
王仲奇,男,1963年生。西北工业大学机电学院教授、博士研究生导师。研究方向为飞机数字化装配工艺技术与装备。李诚(通信作者),男,1993年生。西北工业大学机电学院硕士研究生。E-mail: licheng2014@mail.nwpu.edu.cn。杨勃,男,1986年生。西北工业大学机电学院博士研究生。杨元,男,1989年生。西北工业大学机电学院博士研究生。

