高校公选课学生成绩分析中的幂率分布

陈向阳++旬永俊+++沈超

摘要：高校考试成绩分析中大多数人会习惯性地将学生成绩想象成按照概率统计正态分布的。通过大量数据分析说明，这种分布尽管比较适合文科学生，但并不适用于所有学生尤其是理工科学生。通过分析我们发现针对理科学生公选课成绩分析更合适的分布是网络科学的逆幂律分布而非正态分布。因此该结论学生成绩分析和教学质量评估都有一定的积极意义。

关键词：正态分布；逆幂率分布；网络科学；成绩分析

中图分类号：TP311.52

1 前言

作者多年的学习和教学生涯中遇到很多教师，大家似乎都司通见惯一条钟形曲线正态分布曲线适用于所有文理工科学生的成绩分析，但是我们从来没有见过任何分数分布钟形曲线的实证；教师仅只是盲目地将它强加到课堂成绩分数分析上，相信这才是要做的唯一正确的事情。但事实果真如此吗？

2 问题的提出

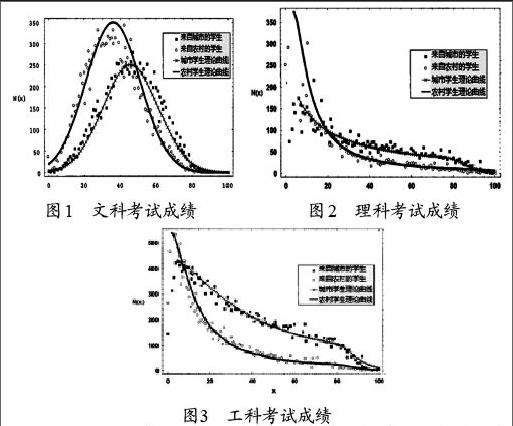
某大学数据分析了1，200名参加了某大学的公选课程成绩测试。在图1中，公选课考试的文科学生成绩部分。在多年的成绩分数比较中，虽然具体分布峰值移动，分布的宽度也会有所移动，但很显然钟形曲线能够对数据进行惊人的拟合。

图1图2图3在近1200名学生公选课考试成绩，为文科理科工科学生绘图。图1似乎支持正态分布适用于描述大量各种社会条件下学生的成绩分数分布的猜想。但是我们从查阅的资料中还没有见到来自科学上的严格证实。在图2中来自理科数据绘制成与在图1中文科的数据放在相同的分组。从图2中有一点可以明确，即成绩分数分布与钟形曲线有着很大的不同。但仅有这些数据其成绩分数分布不是正态的吗？图3描述在同一套分组下工科的分数分布。事实上，理工科的分数分布不像文科的分数分布。没有明显峰值，也没有围绕特征平均值的分数聚集，分数似乎占据着从开始扩展至消失值区间的所有值。

3 分析

为什么常态标准化分布显然适用于文科，而不适用于理工科呢？在文科和理工科之间分数分布的差异的一个可能的解释，是因为两类之间有着结构性的差异。文科的大标题下，包括语言、哲学、社会学、经济学和一些其他相对独立的研究领域的不相交学科组。我们使用术语独立，是因为在社会学中所学是不依赖于经济學中所学知识，但可能比较弱地取决于在语言中所学知识。因此，在这些独立的学科，每年取得的成绩分数是相对独立的，从而满足高斯参数的条件。在满足高斯条件的文科的分数分布就会呈现正态分布。另一方面，理工科是建立在以前所学知识基础之上的。没有代数知识就不能理解基础物理，没有微积分就不能理解更高级的物理学，这也需要理解代数。同样，理解工科课程，需要掌握某种程度的数学、化学和物理学。理工科的学科，形成一个互连知识网络，从最基本的开始构建起来，这种情况违反高斯假设的独立性和平均值能够提供过程最佳描述的想法。在理工科中的成绩分数经验分布清楚地表明扩展了到分布的尾部，从而不存用来描述数据的特征尺度如所谓的平均值[1][2]。在文科和理工科成绩分数分布之间的区别就是明确的证据表明，正态分布并不能用来描述一般或正常情况。分数的钟形曲线是在人们先入为主的偏见通过所谓正统教育所强加的，并不能显示学生掌握知识的过程。所以我们是否可以使用为推导正态分布的论据之一来获得带有在图2和图3中所示的长尾的经验分布吗？让我们重新考虑熵最大化，但会从略有不同的角度来看。熵最大化参数有三个组成部分：（1）熵的定义；（2）限制分布的实证数据的矩；（3）通过最大化从（2）中数据确定拉格朗日乘式。下面就让我们用更一般的观察来取代步骤（2），即理科的分数分布没有一个特征模式标度。我们通过一个缩放函数也就是对数来引入条件[3][4]。那么可变的量为

因此，熵最大化参数能确定一种没有特征标度的分布，在最初源是有限的，并且针对由双曲分布（2）式给出的其余部分是最大限度地随机的，它将渐近逆幂律分布 。

4 结论

上述这种双曲线分布具有一种在理工科公选课程分数分布中观察到的厚尾分布。因此，要审慎地探讨正态分布和双曲分布之间的差异，以了解他们所代表的各种现象的特殊性。最终结论是高校理工科公选课程成绩分数分布可用逆幂律分布尾部来描述。事实上，过去高校成绩分数分析不加区别地应用正态分布的地方，大部分情况下都会发现是由于简化假设导致的结果，往往盲目地使用了数据不支持的钟形曲线的结果。

参考文献

[1] R. Albert and A.-L. Barabási，“Statistical mechanics of complex networks，” Rev. Mod. Phys.74， 48 （2002）.

[2] H. M. Gupta， J. R. Campanha and F. R. Chavorette， “Power-law distribution in high school education： effect of economical， teaching and study conditions，” arXiv.0301523v1 （2003）.

[3] M. E. J. Newman， “The structure and function of complex networks，” SIAM Rev. 45， 167（2003）.

[4] B. J. West， E. L. Geneston and P. Grigolini， “Maximizing information exchange between complex networks，” Physics Reports 468， 1–99 （2008）.endprint