优化动量实验方案 创新设计实验过程

王金兵

摘 要：掌握常规考法，关注实验创新，对比研究了动量守恒定律实验的几种设计方案。通过常规操作方法和创新操作方法的对比，拓宽学生视野，培养实验能力。

关键词：动量守恒定律；创新；六种方案；能力

动量守恒定律实验是要验证碰撞前后系统的动量之和是否相等。实际实验时可以结合打点计时器知识、光电门知识、圆周运动知识、平抛知识、斜面知识等测量或计算速度，另外导轨可以是斜面、水平气垫导轨等，有多种方案可选。本文拟从常规实验出发，结合以上知识设计几种方案，通过创新实验设计，从而在实验的同时开发智力，拓宽视野，培养能力。

一、导轨与平抛相结合

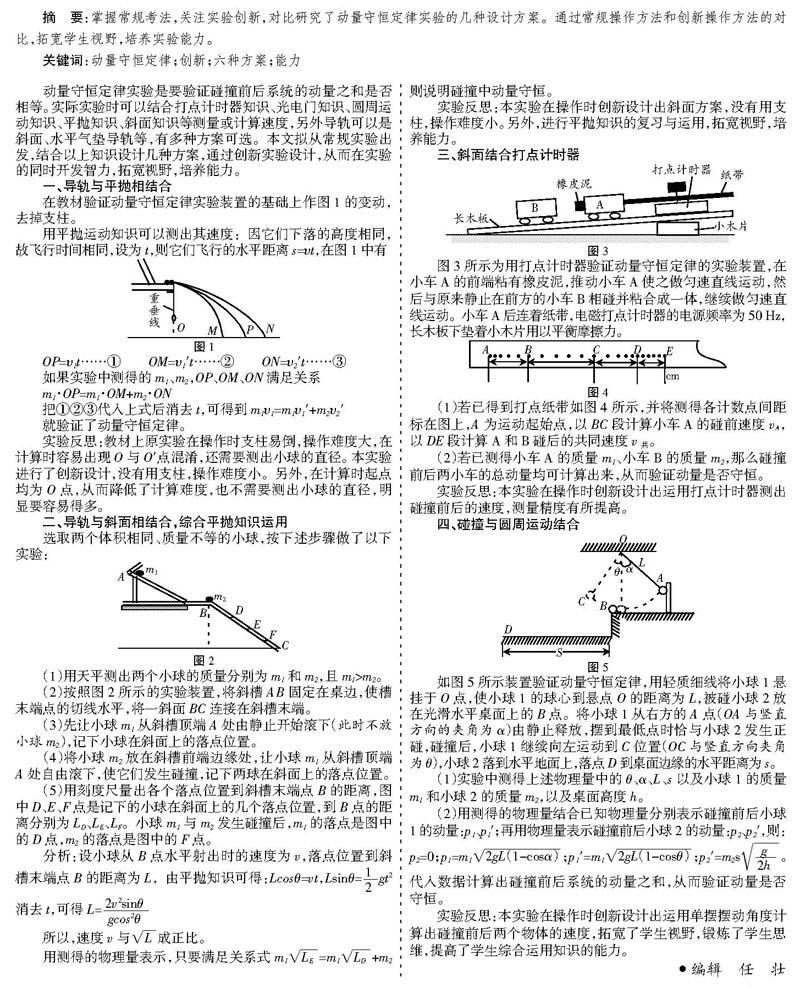
在教材验证动量守恒定律实验装置的基础上作图1的变动，去掉支柱。

用平抛运动知识可以测出其速度：因它们下落的高度相同，故飞行时间相同，设为t，则它们飞行的水平距离s=υt，在图1中有

OP=υ1t……① OM=υ1′t……② ON=υ2′t……③

如果实验中测得的m1、m2，OP、OM、ON满足关系

m1·OP=m1·OM+m2·ON

把①②③代入上式后消去t，可得到m1υ1=m1υ1′+m2υ2′

就验证了动量守恒定律。

实验反思：教材上原实验在操作时支柱易倒，操作难度大，在计算时容易出现O与O′点混淆，还需要测出小球的直径。本实验进行了创新设计，没有用支柱，操作难度小。另外，在计算时起点均为O点，从而降低了计算难度，也不需要测出小球的直径，明显要容易得多。

二、导轨与斜面相结合，综合平抛知识运用

选取两个体积相同、质量不等的小球，按下述步骤做了以下实验：

（1）用天平测出两个小球的质量分别为m1和m2，且m1>m2。

（2）按照图2所示的实验装置，将斜槽AB固定在桌边，使槽末端点的切线水平，将一斜面BC连接在斜槽末端。

（3）先让小球m1从斜槽顶端A处由静止开始滚下（此时不放小球m2），记下小球在斜面上的落点位置。

（4）将小球m2放在斜槽前端边缘处，让小球m1从斜槽顶端A处自由滚下，使它们发生碰撞，记下两球在斜面上的落点位置。

（5）用刻度尺量出各个落点位置到斜槽末端点B的距离，图中D、E、F点是记下的小球在斜面上的几个落点位置，到B点的距离分别为LD、LE、LF。小球m1与m2发生碰撞后，m1的落点是图中的D点，m2的落点是图中的F点。

分析：设小球从B点水平射出时的速度为v，落点位置到斜槽末端点B的距离为L，由平抛知识可得：Lcosθ=vt，Lsinθ=■gt2消去t，可得L=■

所以，速度v与■成正比。

用测得的物理量表示，只要满足关系式m1■=m1■+m2则说明碰撞中动量守恒。

实验反思：本实验在操作时创新设计出斜面方案，没有用支柱，操作难度小。另外，进行平抛知识的复习与运用，拓宽视野，培养能力。

三、斜面结合打点计时器

图3所示为用打点计时器验证动量守恒定律的实验装置，在小车A的前端粘有橡皮泥，推动小车A使之做匀速直线运动，然后与原来静止在前方的小车B相碰并粘合成一体，继续做勻速直线运动。小车A后连着纸带，电磁打点计时器的电源频率为50 Hz，长木板下垫着小木片用以平衡摩擦力。

（1）若已得到打点纸带如图4所示，并将测得各计数点间距标在图上，A为运动起始点，以BC段计算小车A的碰前速度vA，以DE段计算A和B碰后的共同速度v共。

（2）若已测得小车A的质量m1、小车B的质量m2，那么碰撞前后两小车的总动量均可计算出来，从而验证动量是否守恒。

实验反思：本实验在操作时创新设计出运用打点计时器测出碰撞前后的速度，测量精度有所提高。

四、碰撞与圆周运动结合

如图5所示装置验证动量守恒定律，用轻质细线将小球1悬挂于O点，使小球1的球心到悬点O的距离为L，被碰小球2放在光滑水平桌面上的B点。将小球1从右方的A点（OA与竖直方向的夹角为α）由静止释放，摆到最低点时恰与小球2发生正碰，碰撞后，小球1继续向左运动到C位置（OC与竖直方向夹角为θ），小球2落到水平地面上，落点D到桌面边缘的水平距离为s。

（1）实验中测得上述物理量中的θ、α、L、s以及小球1的质量m1和小球2的质量m2，以及桌面高度h。

（2）用测得的物理量结合已知物理量分别表示碰撞前后小球1的动量：p1、p1′；再用物理量表示碰撞前后小球2的动量：p2、p2′，则：p2=0；p1=m1■；p1′=m1■；p2′=m2s■。代入数据计算出碰撞前后系统的动量之和，从而验证动量是否

守恒。

实验反思：本实验在操作时创新设计出运用单摆摆动角度计算出碰撞前后两个物体的速度，拓宽了学生视野，锻炼了学生思维，提高了学生综合运用知识的能力。

编辑 任 壮