改进的堆石坝变形计算参数敏感性分析方法
陈 辉,刘东海,戚 蓝
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
改进的堆石坝变形计算参数敏感性分析方法
陈 辉,刘东海,戚 蓝
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
为提高邓肯-张E-B模型计算堆石坝变形的精度,提出基于全域有限元计算节点的单因素分析方法和基于双判别方式的正交试验方法,分析大坝变形对坝料密度和模型参数的敏感性,确定大坝变形计算的主要影响参数。实例分析表明,φ0、Kb、ρ、Rf、K等对大坝变形的影响显著,故需重点研究这5个参数在空间上的差异性。该研究方法解决了传统单因素分析方法样本缺乏代表性的弊端,可以定量给出参数敏感性的显著性水平,提高了敏感性分析的全面性和准确性,可为堆石坝变形精细分析时合理选择需进行空间赋值的模型参数提供依据。
堆石坝;大坝变形;邓肯-张模型;模型参数;敏感性分析;正交试验法
堆石坝是一种重要坝型,能适应较复杂的地质条件[1]。目前,非线弹性模型——邓肯-张E-B模型在堆石坝变形计算中得到广泛应用[2],其模型设计参数的获取主要依靠三轴试验。大坝实际施工时会受到各种人为因素的影响,从而导致坝料实际压实质量与设计压实质量差别较大[3],同时已有研究表明坝料压实质量(干密度、孔隙率)会影响其力学参数[4]。因此,同分区采用一致的设计参数进行计算,不能反映实际施工情况下堆石坝压实程度的空间差异性。钟登华等[5-6]研制的数字大坝系统可以通过实时采集坝体填筑的过程参数来呈现坝体密实度的空间差异性。已有研究表明坝料压实质量(密度)与其变形特性关系密切[7],因此基于数字大坝系统回归的坝体任意位置的密度[8-9]可以建立其与邓肯-张模型参数的回归关系,进而可以实现一个有限元单元对应一组模型参数的精细模拟。为减少模型参数空间赋值工作量,需寻求最重要的影响参数。同时,大坝施工过程的变形计算反演分析也需寻求最重要的影响参数。因此,分析参数敏感性显得尤为必要。
目前常用的敏感性分析方法有2种:(a)单因素分析法,该方法假定其他参数不变分析某一参数的变化对计算结果的影响。(b)正交试验法,它可以在不影响试验效果的前提下,尽可能地减少试验次数。如,赵国军等[10]采用单因素分析法对坝体中心处的节点进行敏感性分析,得出围压为大气压时的摩擦角φ0、破坏比Rf、弹性模量数K对竖向位移的敏感性最强的结论;吴长彬等[11]基于正交试验法分析堆石坝中部3个节点的参数敏感性,得出φ0、体积模量数Kb、体积模量指数m、弹性模量指数n为影响堆石坝垂直位移的主要参数;恩戈科[12]通过对特定节点采用单因素分析法进行位移函数关系拟合,得出K、Kb、m、n为对位移敏感性最强的参数;李炎隆等[13]采用正交试验极差分析法进行敏感性分析,得出φ0、Rf、K、Kb对坝体变形影响显著的结论。由此可见,上述研究得出的敏感性结论并不一致,说明更为全面而深入的敏感性分析很有必要。
单因素分析法采用个别节点的位移作为研究样本进行敏感性分析,样本位置选择的不同会导致敏感性分析结论的不同。另外,上述采用正交试验法的研究并没有设置误差列,因此未能得到敏感性分析的定量结果。同时,当前研究没有分析坝料密度差异对大坝变形计算的影响,然而在施工过程中大坝空间密度差异是普遍存在的,因此有必要对坝料密度连同邓肯-张E-B模型参数一起进行分析。为解决上述问题,笔者基于全域有限元节点的单因素敏感性分析方法和基于双判别方式的正交试验敏感性分析方法对坝料密度和邓肯-张模型参数的敏感性进行分析。
1 基于全域有限元计算节点的单因素参数敏感性分析
邓肯-张E-B模型表达式如下[14]:
(1)
式中:Et——切线模量;S——应力水平;c——粘聚力;φ——内摩擦角;Pa——大气压力;σ1——大主应力;σ3——小主应力。
对于无黏性粗粒土c=0,在堆石坝数值分析中采用非线性强度参数:
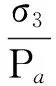
(2)
式中:Δφ——围压相当于标准大气压增大10倍时摩擦角的减小量。
材料的体积模量为
(3)
单因素敏感性分析的具体步骤如下:(a)确定研究对象。选择主堆石区全域节点的位移情况为研究对象。位移包括水平位移与竖向位移,竖向位移为垂直向下的沉降,水平位移分为向上游的变形和向下游的变形。(b)确定试验因素、因素水平。选择邓肯-张模型中的φ0、Δφ、Rf、K、n、Kb、m以及密度ρ总共8个参数进行敏感性分析。以设计参数为基准参数,模型计算参数取0(基准参数)、30%以及-30%的增减量作为试验水平。ρ取0(基准参数)、20%以及-20%的增减量作为试验水平。(c)有限元计算。将邓肯-张模型中的单个参数作为变量进行多组有限元计算。(d)结果分析。统计计算各个工况下位移变化差异值与变化率的平均值来衡量各个参数的敏感性情况。其中,位移变化差异值为参数变化时各个节点的位移减去基准参数下对应节点的位移,位移变化率为参数变化时节点的位移差异值与基准参数下对应节点的位移值之比的绝对值。
2 基于双判别方式的正交试验参数敏感性分析
采用基于双判别方式(极差判别与方差判别)的正交试验设计对堆石坝变形计算的参数进行敏感性分析,同时给出2种判别方式结果的异同点。步骤如下:
a. 确定试验指标。选择坝体主堆石区的最大竖向位移V、向上游最大水平位移H1和向下游最大水平位移H2等宏观指标作为敏感性分析的指标。
b. 确定试验因素、因素水平。选择φ0、Δφ、Rf、K、n、Kb、m及ρ总共8个参数进行敏感性分析。以设计参数为基准参数,在敏感性分析中每个计算参数按0(基准参数)、30%、20%以及-20%的增减量作4个试验水平。
c. 选择合适的正交表。根据试验因素个数和因素水平数,选择L32(49)(即可以安排9因素4水平数,需要做32次试验)正交表安排试验(设置一列误差列)。计算每种方案下的试验指标V、H1和H2,设计正交试验方案。
d. 对结果采用直观分析法进行分析。通过极差统计找出主要影响参数以及次要影响参数。极差值Rj为某因素在对应水平下Kij(因素j在i水平下各次试验结果之和)的最大值与最小值的差值[15]。Rj越大表明该因素的敏感性越强。
e. 对结果采用方差分析法进行分析。该方法可以给出因素对试验指标影响程度的量化结果。其分析步骤如下:(a)计算总偏差平方和ST和各列偏差平方和Sj及各列自由度fj。(b)计算各因素列平均偏差平方和Vj(Vj=Sj/fj)和误差列平均偏差平方和Ve。(c)计算各因素的F检验的Fj(Fj=Vj/Ve)值,根据Fj的大小进行敏感性分析排序,Fj越大说明影响越显著,即敏感性越强。
3 工程实例分析
3.1工程概况

图1 坝体典型剖面与主堆石区有限元计算节点Fig.1 Typical dam section and finite element nodes of the main rock-fill area
某工程为混凝土面板堆石坝,坝顶高程为295.00 m,坝顶宽为10 m,最大坝高为 165.00 m,上游面坡比为 1∶1.4,下游面坡比为 1∶1.45。大坝典型剖面和主堆石区有限元1 215个计算节点如图1所示。
3.2单因素参数敏感性分析
3.2.1 试验设计与有限元计算
选择堆石坝主堆石区为研究对象。试验因素和各因素水平见表1。基准参数下有限元计算的大坝位移云图如图2所示。对堆石坝主堆石区的1 215个有限元计算节点(图1)的位移结果进行敏感性统计分析。

表1 主堆石区单因素敏感性分析参数

图2 基准参数下位移云图(单位:m)Fig.2 The calculated displacement contours by using standard parameters(units:m)

图3 参数变化前后主堆石区全部节点位移分布Fig.3 Displacement distribution of all finite element nodes in main rock-fill area before and after parameter changes
3.2.2 敏感性分析
有限元计算完成后对全部节点位移结果进行统计分析,以基准参数计算下的各个节点的竖向位移为横坐标,以Kb增加30%后的对应节点的竖向位移为纵坐标作图,如图3所示。可以看出Kb增加前后二者位移结果符合线性关系,其趋势线在y=x上方,说明随Kb的增加,节点的竖向位移的增量为正,即坝体竖向变形将会减小。
由图3可以得到竖向位移变化率:
(4)
由式(4)可知,不同位置节点的竖向位移变化率并不相同,从而同一模型参数的敏感性会随着所选节点的位置而变化。为了得到准确的敏感性结论,需要统计节点的平均位移变化差异值与变化率。
图4分别给出了竖向位移、向上游的水平位移以及向下游的水平位移所对应的邓肯-张E-B模型参数和坝料密度敏感性分布。

图4 参数敏感性分布Fig.4 Parameters sensitivity distribution
位移变化率平均值及位移变化差异平均值的绝对值越大,说明参数的敏感性越强。因此,由图4可知,对竖向位移变化敏感的参数是φ0、Kb、ρ、Rf,对向上游发生水平变形的敏感性强的参数是φ0、K、Rf、ρ、Kb,对向下游发生水平变形的敏感性强的参数是φ0、Rf、K、Kb。即对变形较为敏感的参数为φ0、Kb、ρ、Rf、K,而m、n、Δφ对位移变化的敏感性不强。从竖向位移的变化平均差异值曲线可以看出,参数φ0、Kb、K增加,竖向变形将减小(位移增大)。
3.3正交试验参数敏感性分析
3.3.1 试验设计与有限元计算
正交试验因素和各因素水平如表2所示。试验方案及有限元计算结果如表3所示。

表2 正交试验因素水平参数取值

表3 正交试验设计方案及计算结果
3.3.2 计算结果分析
对指标V的影响因素做极差分析,结果如表4所示。结果显示,各因素对指标V的敏感性由强到弱依次为:φ0、Kb、ρ、Rf、n、m、K、Δφ。
对指标V的影响因素做方差分析(表5),各因素对指标V的敏感性由强到弱依次为:Kb、φ0、ρ、Rf、n、m、K、Δφ。

表5 指标V影响因素方差分析结果
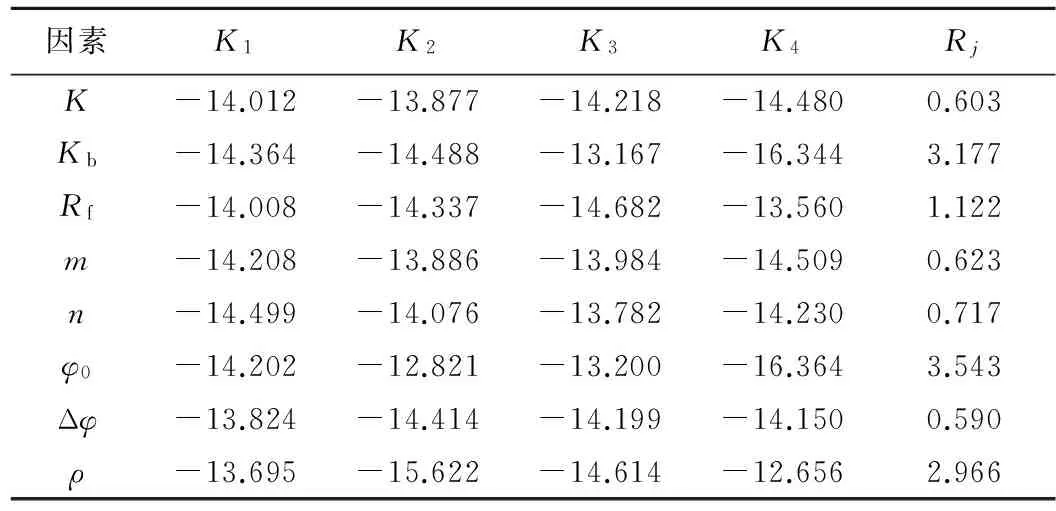
表4 指标V影响因素极差分析结果
同理,对指标H1的影响因素做极差分析,各因素对指标H1的敏感性由强到弱依次为:φ0、Rf、K、n、ρ、Δφ、Kb、m。对指标H1的影响因素做方差分析,各因素对指标H1的敏感性由强到弱依次为:φ0、Rf、K、n、ρ、Δφ、Kb、m。对指标H2的影响因素做极差分析,各因素对指标H2的敏感性由强到弱依次为:φ0、ρ、K、Rf、Kb、Δφ、m、n。对指标H2的影响因素做方差分析,各因素对指标H2的敏感性由强到弱依次为:φ0、ρ、Rf、K、m、Kb、Δφ、n。因此,对最大竖向位移的参数敏感性排序,方差分析与极差分析得出的敏感性顺序不一致,但二者均得出φ0、Kb、ρ、Rf是敏感性最强的4个参数。对向上游的最大位移参数敏感性排序,方差分析与极差分析得出的结论一致;对向下游的最大位移的参数敏感性排序,方差分析与极差分析得出的敏感性顺序不一致,但二者均得出φ0、ρ、K、Rf是敏感性最强的4个参数。
将单因素敏感性分析结果与正交试验敏感性分析结果进行排序对比,如表6所示。分析单因素分析法的2种情况(参数增加和参数减小),发现二者的排序方法也不是完全一致的,说明变形随参数的变化并不是线性变化的,选择的参数变化区间的范围对分析结果是有影响的。比较单因素方法与正交试验法结果可以看到,虽然二者的参数敏感性排序不完全一致,但是总体结果是一致的:对变形较为敏感的参数为φ0、Kb、ρ、Rf、K,对位移变化的敏感性不强的参数为m、n、Δφ。

表6 单因素分析方法与正交试验法敏感性分析结果排序对比
3.4规则大坝剖面算例研究
上述研究是基于建基面有较大的向下游倾斜坡度的特定工程的研究,为了验证分析结果是否具有普遍适用的意义。设计简单的具有规则断面的均质堆石坝,高100 m,坝顶宽10 m,上下游坝坡坡比为1∶2。设计参数下的有限元计算结果如图5所示。

图5 规则大坝剖面基准参数下位移云图(单位:m)Fig.5 The calculated displacement contours by using standard parameters of regular dam section(units:m)
按照与3.2节、3.3节完全相同的步骤进行计算分析,最终得到如表7所示的敏感性分析结果。

表7 规则大坝剖面的敏感性分析结果
由表7可知,不同坝体形状会导致敏感性排序的不同,但是总体结果是一致的,即φ0、Kb、ρ、Rf、K等参数对大坝的变形影响显著。
4 结 语
提出基于全域有限元节点的单因素敏感性分析方法和基于双判别方式的正交试验敏感性分析方法。基于堆石坝分区剖面的全部节点位移情况进行统计分析,比传统单因素方法采用的选择特殊位置个别节点进行分析更具说服力。采用基于双判别方式的正交试验设计对堆石坝变形参数进行敏感性分析,给出敏感性显著性水平的定量结果,比仅依靠极差判别更为全面。研究可知坝体不同部位的位移对相同模型参数敏感性不同,样本点的选择会影响分析结论,因此使用全域有限元节点分析是必要的。正交试验的极差分析与方差分析结果基本一致。比较单因素方法与正交试验法结论可以看到,虽然二者参数敏感性排序不完全一致,但是总体结果是一致的:即对大坝变形变化敏感的参数是φ0、ρ、K、Rf、Kb。同时,坝体断面形式的不同会导致参数敏感性排序的不同,但总体分析结论仍然是一致的,说明论文提出的敏感性结论具有普遍的适用意义。分析结果显示坝料密度对坝体变形的影响是非常显著的,因此忽略密度的参数敏感性分析是不科学的。通过分析可知,需重点研究φ0、Kb、ρ、Rf、K这5个参数在空间上的差异性,同时可以将这几个参数作为反演分析对象,从而为堆石坝变形有限元精细分析时空间赋值模型参数的选择以及后续反演分析提供参考依据。
[ 1 ] 褚福永, 朱俊高, 张富有,等. 300m级弧形直心墙超高堆石坝应力变形分析[J].河海大学学报(自然科学版), 2011,39(5): 506-510. (CHU Fuyong, ZHU Jungao, ZHANG Fuyou, et al. Stress and deformation analysis of 300 m-level high rockfill dam switch arc and vertical cores[J]. Journal of Hohai University(Natural Scineces), 2011, 39(5): 506-510. (in Chinese))
[ 2 ] 朱敏,邓华锋,许晓亮.基于子模型法的面板堆石坝三维应力变形分析[J].水利水电科技进展,2012, 32(6): 27-30. (ZHU Min, DENG Huafeng, XU Xiaoliang. 3D stress-deformation analysis of CFRDs based on sub-model method[J]. Advances in Science and Technology of Water Resources, 2012, 32(6): 27-30. (in Chinese))
[ 3 ] 刘东海, 王倩, 崔博, 等. 连续监控下土石坝碾压参数的控制标准及其确定方法[J]. 岩土工程学报, 2013, 35(9): 1712-1716.(LIU Donghai, WANG Qian, CUI Bo, et al. Control standards for compaction parameters of earth-rock dams under continuous construction process monitoring[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(9): 1712-1716. (in Chinese))
[ 4 ] 傅华, 陈生水, 凌华, 等. 高应力状态下堆石料工程特性试验研究[J]. 水利学报, 2014,45(增刊2): 83-88.(FU Hua, CHEN Shengshui, LING Hua, et al. Experimental study on engineering properties of rockfill under high stress state[J]. Journal of Hydraulic Engineering, 2014,45(Sup2): 83-88.(in Chinese))
[ 5 ] ZHONG Denghua, CUI Bo, LIU Donghai, et al. Theoretical research on construction quality real-time monitoring and system integration of core rockfill dam[J]. Science in China Series E:Technological Science, 2009, 52(11): 3406-3412.
[ 6 ] ZHONG Denghua, LIU Donghai, CUI Bo. Real-time compaction quality monitoring of high core rock-fill dam[J]. Science China Technological Sciences, 2011, 54(7): 1906-1913.
[ 7 ] 徐泽平. 混凝土面板堆石坝应力变形特性研究[M]. 郑州: 黄河水利出版社, 2005.
[ 8 ] LIU Donghai, SUN Jing, ZHONG Denghua. Compaction quality control of earth-rock dam construction using real-time field operation data[J]. Journal of Construction Engineering and Management, ASCE, 2012, 138(9): 1085-1094.
[ 9 ] LIU Donghai, LI Zilong, LIAN Zhenhong. Compaction quality assessment of earth-rock dam materials using roller-integrated compaction monitoring technology[J]. Automation in Construction, 2014, 44(8): 234-246.
[10] 赵国军, 翟守俊. 邓肯-张 E-B 模型参数对心墙土变形的敏感性研究[J]. 资源环境与工程, 2012, 26(5): 514-516.(ZHAO Guojun, ZHAI Shoujun. Sensibility analyses of the Duncan-Chang E-B model parameters to deformation of core wall soil[J]. Resources Environment & Engineering, 2012, 26(5): 514-516. (in Chinese))
[11] 吴长彬, 燕乔. 堆石料的邓肯E-B模型参数敏感性分析[J]. 水电能源科学, 2010, 28(8): 94-96.(WU Changbin, YAN Qiao. Sensitivity analysis of Duncan-Chang E-B model parameters for rockfill[J]. Water Resources and Power, 2010, 28(8): 94-96. (in Chinese))
[12] 恩戈科. 堆石坝材料参数的灵敏度分析[J]. 河海大学学报(自然科学版), 1999, 27(5): 94-99.(EN Geke. Sensitivity analysis of parameters for rockfill dams[J]. Journal of Hohai University(Natural Sciences), 1999, 27(5): 94-99. (in Chinese))
[13] 李炎隆, 李守义, 丁占峰, 等. 基于正交试验法的邓肯-张E-B模型参数敏感性分析研究[J]. 水利学报, 2013, 44(7): 873-879.(LI Yanlong, LI Shouyi, DING Zhanfeng, et al. The sensitivity analysis of Duncan-Chang E-B model parameters based on the orthogonal test method[J]. Journal of Hydraulic Engineering, 2013, 44(7): 873-879. (in Chinese))
[14] 关志诚.水工设计手册(第6卷)土石坝[M].北京:中国水利水电出版社, 2014.
[15] 邱轶兵. 试验设计与数据处理[M]. 合肥: 中国科学技术大学出版社, 2008.
Improvedsensitivityanalysismethodforcalculatingthedeformationparametersoftherock-filldam
CHENHui,LIUDonghai,QILan
(StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China)
To improve the calculation accuracy of the Duncan-Chang E-B model regarding the deformation of the rock-fill dam, the single factor analysis method based on finite element calculation nodes in the whole zone of the computational dam is proposed together with the orthogonal experimental method based on the double discriminant method in this study. The sensitivity of dam deformation due to the compacted density of dam and the model parameters is studied, so as to ascertain the main influencing parameters of the dam deformation. A case study indicates that the dam deformation is significantly influenced by five parameters i.e.φ0,Kb,ρ,RfandK, and their spatial differences deserve further research with emphasis. The methods proposed in this paper overcome the disadvantages of traditional single factor method, in which the samples are lack of representatives. With these methods, the significance level of parameters sensitivity can be determined in a quantitative way, thus improving the comprehensiveness and precision of the sensitivity analysis and providing some reference for the reasonable selection of model parameters that require spatial assignment in the refined analysis of rock-fill dam deformation.
rock-fill dam; dam deformation; Duncan-Chang model; model parameters; sensitivity analysis; orthogonal experimental method
10.3876/j.issn.1000-1980.2017.05.005
2016-09-29
国家自然科学基金面上项目(51479132,51679164);国家自然科学基金创新群体研究项目(51321065)
陈辉(1990—),男,山东郓城人,博士研究生,主要从事水工结构方面研究。E-mail:chwx@tju.edu.cn
刘东海,教授。E-ail:liudh@tju.edu.cn
TV641.4
A
1000-1980(2017)05-0406-07

