岩石统计损伤本构模型与试验
王苏生,徐卫亚,王 伟,王如宾,向志鹏
(1. 河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098; 2. 河海大学岩土工程科学研究所,江苏 南京 210098)
岩石统计损伤本构模型与试验
王苏生1,2,徐卫亚1,2,王 伟1,2,王如宾1,2,向志鹏1,2
(1. 河海大学岩土力学与堤坝工程教育部重点实验室,江苏 南京 210098; 2. 河海大学岩土工程科学研究所,江苏 南京 210098)
基于Mohr-Coulomb破坏准则以及岩石微元强度服从Weibull函数随机分布假设,通过有效应力原理引入孔隙水压力,构建了新的统计损伤本构模型,该模型可以考虑孔隙体积变化和损伤阀值的影响。此外,提出了一种新的岩石微元强度计算方法。为使模型参数具有明确的物理意义,采用应力~应变曲线峰值点强度确定模型参数m和F0。采用砂岩常规三轴压缩试验对本构模型的合理性进行验证,并在此基础上,分析岩石损伤演化、孔隙率变化规律,探讨围压对模型参数的影响。结果表明,该模型能够较好地反映岩石三轴应力~应变关系。
岩石力学;Mohr-Coulomb准则;Weibull分布;微元强度;统计损伤模型
岩体是一种复杂的天然地质体,内部含有微裂纹、空穴和节理等,其微裂纹的发育情况直接影响水的渗透能力[1]。流体在岩石内部运动是一个复杂问题,为了更深层次了解渗透规律,前人进行了大量科学试验研究。许江等[2]通过对砂岩进行循环孔隙水压力试验,研究了砂岩变形特性以及孔隙水压力在循环过程中的作用机制,得出循环次数对变形特性的影响规律。王如宾等[3-5]开展了不同围压和渗压作用下岩石流变力学试验研究,并结合试验初步探讨流变过程中渗透演化规律。王伟等[6-7〗[8]得出不同围压条件下力学损伤演化机制及其对岩石渗透特性影响规律。研究结果表明,渗流作用使得岩石结构发生变化,从而导致岩石渗透性和力学特征发生改变。
岩石材料具有明显的非均匀性,内部随机分布的缺陷导致力学性质有很大差异。用细观方法研究岩石微裂隙,结合统计学原理研究损伤是一种较好的研究方法。Krajcinovi等[9]从岩石材料内部的缺陷随机分布出发,利用岩石微元强度服从Weibull分布,建立了岩石破裂过程的统计损伤本构方程。徐卫亚等[10-11]基于概率统计和损伤力学对岩石强度和变形特性等进行分析,并构建了统计损伤本构模型。ZHAO等[12],CAO等[13],蔡新等[14]考虑体积变化的影响,从而使得本构模型有了进一步发展。有关渗流作用下的统计损伤理论研究较少,仅王伟等[15-16]构建了能考虑孔隙水压力作用的损伤统计本构模型。
笔者在前人研究基础上,基于Mohr-Coulomb破坏准则及岩石微元强度服从Weibull函数随机分布,构建渗流作用下新的岩石统计损伤本构模型,提出新的岩石微元强度计算方法。
1 模型构建及参数辨识
1.1统计损伤模型构建
在多孔介质弹性理论中,一般采用有效应力原理分析渗流作用问题。Terzaghi[17]提出的有效应力原理是研究应力和孔隙水压力作用下岩土介质整体宏观力学响应的一个基本方程:

(1)
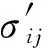
Lemaitre[18]假定损伤是各向同性,则它对柯西应力张量的所有张量都有相同的影响,可建立考虑损伤岩石净应力表达式为
(2)
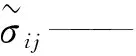

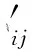
(3)
现阶段大多数弹塑性本构模型都忽略初始压密过程,只考虑岩石发生屈服变形前的线性阶段。然而,岩石内部含有大量的裂隙和孔隙,特别是对于孔隙率较大的岩石,初始压密过程较明显,同时岩石在加载过程中,会出现体积扩容现象,因此,定义在主应力空间考虑孔隙水压力和孔隙体积变化的本构方程:
(4)

假定岩石损伤后的岩石材料不承受荷载,则由式(4)可得出如下岩石损伤模型:
(5)
加载过程中的孔隙率n采用体积应变和初始孔隙率进行计算。

(6)
式中:εv——瞬时体积应变;n0——初始孔隙率,可以通过测岩样干重和饱和后湿重确定。
由式(1)(2)(3)(5)可得考虑渗流作用下考虑孔隙体积变化的有效应力为
(7)
(8)
式中:v——泊松比。
将式(7)代入(8),可得出岩石在孔隙水压力作用下的损伤本构关系:
σ1=Eε1(1-D)(1-n)+v(σ2+σ3)+(1-2v)pw
(9)
在常规三轴试验中(σ2=σ3),式(9)可简化为
σ1=Eε1(1-D)(1-n)+2vσ3+(1-2v)pw
(10)
考虑静水孔隙水压力的三轴压缩试验,通常是先施加围压到预定值,然后再施加偏应力直至岩样破坏。因此在施加偏应力之前轴向会产生一个初始应变ε10,偏应力~应变曲线不包括此段应变。为了真实反映应力~应变关系,需要考虑初始应变。试验中记录的轴向偏应力σ1t实际上是轴向应力σ1和围压σ3的差值,即
σ1t=σ1-σ3
(11)
渗流作用下,初始应变ε10可以根据广义虎克定律进行计算如式(12)所示。
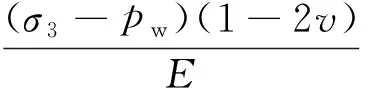
(12)
因此,加载过程中的轴向真实应变为
ε1=ε1t+ε10
(13)
式中:ε1t——偏应力产生的应变。
将是式(11)和(13)代入式(10),得到渗流作用下,岩石统计本构模型为
σ1t=E(ε1t+ε10)(1-D)(1-n)+(1-2v)(pw-σ3)
(14)
假定岩石微元强度服从Weibull随机分布,建立考虑损伤阀值影响的岩石统计损伤变量D可表示为
(15)
式中:m、F0——Weibull分布函数参数;F——岩石微元强度随机分布变量。

(16)
基于Mohr-Coulomb破坏准则的岩石微元强度准则的计算方法,如下式:

(17)
式中:φ、c——岩石的摩擦角和黏聚力。
为方便计算,考虑孔隙水压力作用下微元强度准则改写成:

(18)
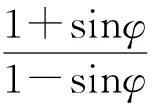

(19)
结合广义虎克定律和式(19),可得
F=E(ε1t+ε10)+(2v-α)σ3-(1-α)pw-k0
(20)
将式(16)代入式(14),可得到考虑孔隙水压力应用于三轴压缩条件下的岩石统计损伤本构模型:
(21)
1.2模型参数辨识
根据应力~应变曲线的峰值点强度确定模型参数。此方法确定的模型参数物理意义明确,且适用于不同类型的岩石模型参数确定。因此,本文采用峰值点强度确定模型参数的计算方法进行参数识别。岩样的应力~应变曲线峰值点处对应的应力、大主应变和体积应变值变分别为σ1c、ε1c和εvc,其微元强度为Fc。即满足条件式(22)(23)(24)。
ε1t=ε1c
(22)
σ1t=σ1c
(23)
(24)
将式(20)(21)代入式(22)(23)和式(24),从而确定模型参数:

(25)

2 试验与模型验证
2.1试验

图1 三轴压缩仪器示意图Fig.1 Schematics the triaxial apparatus
为对本文提出的岩石统计损伤本构模型的有效性进行验证,采用伺服试验机对砂岩样进行了一组不同围压的三轴压缩试验。砂岩常规三轴压缩试验在河海大学试验中心多功能岩石三轴测试系统上进行,仪器示意图如图1所示。采用轴向位移传感器(LVDTs)实时记录试样轴向变形。其中位于仪器顶部的位移传感计D1用来测量压头位移,压力室底座上的2个位移传感器D2和D3用来测量岩样的轴向变形。岩样的环形变形由环向应变计测量。本试验装置最大围压达到60 MPa,最大偏压达到500 MPa,变形测量系统的测控精度达到了微米级。根据国际岩石力学学会(ISRM)[19],将选取的砂岩原状样切割打磨,制备成上下端面水平,侧面光滑的50 mm×100 mm圆柱样,岩样如图2所示。
试验前,首先将砂岩样烘干测干重,其次对试样抽真空充水饱和,并测量饱水后试样的湿重,计算其初始孔隙率n0分别是3.84%,3.15%和2.85%。将围压加载至预定值(10 MPa、15 MPa、20 MPa),待围压稳定后,将渗压加载至6 MPa进行饱水直到渗流通道有水流出,开始轴向加载至试样破坏。加载速率为0.02 mm/min。试样破坏后如图3所示,其破坏形式为单截面剪切破坏。

图2 原状砂岩试样Fig.2 Specimens of intact sandstone

图3 试样破坏照片Fig.3 Photos of samples after failure
图4给出了砂岩在不同围压下常规三轴渗流压缩试验应力~应变曲线。从图4可以看出,岩石的峰值强度随着围压增加而增大。应力~应变过程分为3个阶段:初始压密阶段、弹性阶段和塑性变形阶段。加载初期,由于砂岩内部初始孔隙逐渐闭合,从试验曲线上看为初始非线性段;随着偏应力的增大,内部裂隙闭合后进入线弹性阶段;随着偏应力进一步增大,岩样内部开始产生裂隙以及裂隙逐步扩展导致塑性变形的产生。由图4可以看出,随着围压的增大,初始压密阶段逐渐不明显。原因在于初始静水压力作用下砂岩样进行压密,内部微裂纹和孔隙逐渐闭合,且随着围压的增加,闭合的越充分。

图4 不同围压下砂岩偏应力~应变关系Fig.4 Relationship between deviatoric stress and strain of sandstone under different confining pressures

围压/MPa渗压/MPaE/GPavmF0/MPa10616.00.234.0698.2315619.80.303.31137.7720623.50.282.28171.99
2.2模型验证
通过室内试验应力~应变曲线进行计算,得出模型参数见表1。根据式(21)得到不同围压同一渗压作用下的砂岩样应力~应变关系理论曲线,并将其与室内试验结果进行对比分析(图5)。从图5可以看出本构模型能够反映出岩样在加载过程中不同阶段的应力应变关系,且理论曲线和室内试验曲线吻合较好。

图5 试验与理论曲线比较Fig.5 Comparison between experimental and theoretical curves
3 讨 论
3.1不同围压下损伤变量演化规律
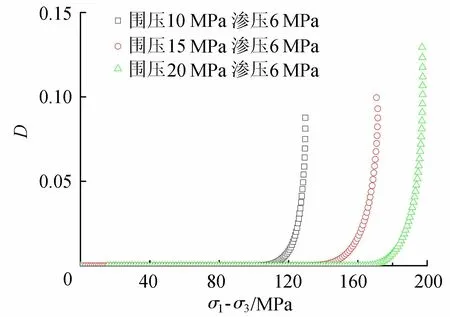
图6 不同围压下的损伤变化Fig.6 Damage evolution under different confining pressures

图7 不同围压下孔隙率与轴向应变关系Fig.7 Relationship between porosity and axial strain under different confining pressures
利用式(15)可得到损伤变量与偏应力的曲线关系,从而得到渗流作用下不同围压的D~σ1-σ3曲线,如图6所示。由于考虑损伤阀值影响,因此当应力水平较低时,损伤变量D为0;当试样所受应力达到一定应力水平,损伤变量开始随着应力的增加而增大,在临近岩样峰值强度时,损伤变量迅速增大。从图6可以看出,不同围压作用下的损伤起始点不同,这是因为采用Mohr-Coulomb强度准则作为损伤随机分布变量,随着围压的增大,屈服点所对应的应力值也会增大,与实际情况相符。
3.2不同围压下孔隙率变化规律
利用式(6)可得到孔隙率与轴向应变的关系,从而绘制不同围压的n~ε1曲线,如图7所示。n随着轴向应变的增大而减小,当轴向变形达到一定值后,孔隙率随着轴向应变增大而增大,在临近岩石峰值强度破坏时,孔隙率明显增大,且破坏后的孔隙率大于初始孔隙率。砂岩样在初始压缩阶段,孔隙率逐渐减小,随着偏应力的逐渐增加,裂隙产生、扩展导致孔隙率逐渐增大,在临近破坏点时,裂隙迅速贯通导致孔隙率快速增大。从图7还可以看出随着围压的增大,孔隙率在临近破坏点时变化越小。
3.3围压和模型参数的关系
对表2中的围压σ3和模型参数进行线性拟合,得到σ3~m和σ3~F0的关系曲线如图8所示。结果表明二者具有良好的线性关系,且m随着围压的增大而减小,F0随围压的增大而增大。
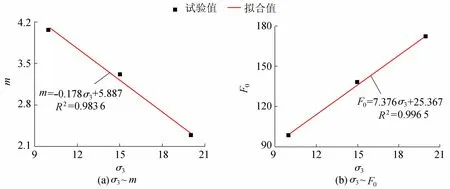
图8 σ3~m、σ3~F0的关系曲线Fig.8 Relationship between σ3 ~m and σ3~F0
4 结 论
a. 构建了考虑静水压力、孔隙率变化和损伤阀值影响的岩石统计损伤本构模型。通过对比分析室内试验和理论计算结果,表明提出的统计损伤本构模型能够较好的反映不同围压条件下的应力~应变关系。
b. 该模型考虑岩石损伤阀值的影响,当应力达到一定水平后,损伤开始产生,在临近岩石峰值强度时,损伤因子迅速增大,并且不同围压作用下的损伤起始点不同。
c. 确定的模型参数m和F0具有明确的物理意义。模型参数与围压σ3呈良好的线性关系,其中m随着围压的增大而减小,F0随围压的增大而增大。
[ 1 ] 徐志英.岩石力学(高等学校教材)[M].3版.北京:水利水电出版社,2007.
[ 2 ] 许江,杨红伟,李树春,等.循环加、卸载孔隙水压力对砂岩变形特性影响实验研究[J].岩石力学与工程学报,2009,28(5): 892-899.(XU Jiang,YANG Hongwei,LI Shuchun,et al.Experimental study of effects of cyclics loading and unloading pore water pressures on deformation characteristic of sandstone [J].Chinese Journal of Rock Mechanics and Engineering,2009,28(5): 892-899.(in Chinese))
[ 3 ] 王如宾,徐卫亚,王伟,等.坝基硬岩蠕变特性试验及其蠕变全过程中的渗流规律[J].岩石力学与工程学报,2010,29(5): 960-969.(WANG Rubin,XU Weiya,WANG Wei,et al.Experimental investigation on creep behaviors of hard rock in dam foundation and its seepage laws during complete process of rock creep [J].Chinese Journal of Rock Mechanics and Engineering,2010,29(5): 960-969.(in Chinese))
[ 4 ] BUI T A, WONG H, DELERUYELLE F,et al.Constitutive modelling of the time-dependent behaviour of partially saturated rocks[J].Computers & Geotechnics,2016,78:123-133.
[ 5 ] 张玉,徐卫亚,邵建富,等.渗流-应力耦合作用下碎屑岩流变特性和渗透演化机制试验研究[J].岩石力学与工程学报,2014,33(8): 1679-1690.(ZHANG Yu,XU Weiya,SHAO Jianfu,et al.Experimental investigation on rheological properties and permeability of clastic rock under hydro-mechanical coupling [J].Chinese Journal of Rock Mechanics and Engineering,2014,33(8):1679-1690.(in Chinese))
[ 6 ] 王伟,徐卫亚,王如宾,等.低渗透岩石三轴压缩过程中的渗透性研究[J].岩石力学与工程学报,2015,34(1): 40-47.(WANG Wei,XU Weiya,WANG Rubin,et al.Permeability of dense rock under triaxial compression[J].Chinese Journal of Rock Mechanics and Engineering,2015,34(1): 40-47.(in Chinese))
[ 7 ] WANG H,XU W,LUI Z,et al.Dependency of hydromechanical properties of monzonitic granite on confining pressure and fluid pressure under compression[J].International Journal of Modern Physics B,2016,30(16):1650086.
[ 8 ] 陈亮,刘建锋,王春萍,等.压缩应力条件下花岗岩损伤演化特征及其对渗透性影响研究[J].岩石力学与工程学报,2014,33(2): 287-295.(CHEN Liang,LIU Jianfeng,WANG Chunping,et al.Investigation on evolution characteristics of granite under compressive stress condition and its impact on permeability [J].Chinese Journal of Rock Mechanics and Engineering,2014,33(2):287-295.(in Chinese))
[ 9 ] KRAJCINOVI C D,SILVA M A G.Statistical aspects of the continuous damage theory[J].International Journal of Solids & Structures,1982,18(7): 551-262.
[10] 徐卫亚,韦立德.岩石损伤统计本构模型的研究[J].岩石力学与工程学报,2002,21(6): 787-791.(XU Weiya,WEI Lide.Study onstatistical damage constitutive model of rock [J].Chinese Journal of Rock Mechanics and Engineering,2002,21(6): 787-791.(in Chinese))
[11] 韦立德,徐卫亚,杨春和,等.具有统计损伤的岩石弹塑性本构模型研究[J].岩石力学与工程学报,2004,23(12): 1971-1975.(WEI Lide,XU Weiya,YANG Chunhe,et al.Study on elastoplastic constitutive model of rock with statistical damage [J].Chinese Journal of Rock Mechanics and Engineering,2004,23(12): 1971-1975.(in Chinese))
[12] ZHAO H,SHI C,ZHAO M,et al.Statistical damage constitutive model for rocks considering residual strength[J].International Journal of Geomechanics,2016,17(1): 04016033.
[13] CAO W G G,ZHAO H Z,LI X L,et al.Statistical damage model with strain softening and hardening for rocks[J].Revue Canadienne De Géotechnique,2010,47(8): 857-871.
[14] 蔡新,杨杰,郭兴文,等.一种胶凝砂砾石坝坝料非线性 K-G-D 本构新模型[J].河海大学学报(自然科学版),2014,42(6):491-496.(CAI Xin,YANG Jei,GUO Xinwen,et al.A new type of nonlinear K-G-D constitutive model for CSG material [J].Journal of Hohai University( Natural Sciences),2014,42(6):491-496.(in Chinese))
[15] 王伟,田振元,朱其志,等.考虑孔隙水压力的岩石统计损伤本构模型研究[J].岩石力学与工程学报,2015,34 (增刊2): 3676-3682.(WANG Wei,TIAN Zhenyuan,ZHU Qizhi,et al.Study of statistical damage constitutive model for rock considering water pressure [J].Chinese Journal of Rock Mechanics and Engineering,2015,34(Sup2): 3676-3682.(in Chinese))
[16] 韦立德,徐卫亚,杨春和,等.饱和、非饱和岩石损伤统计本构模型探讨[J].岩石力学与工程学报,2004,23(增刊1): 4285-4291.(WEI Lide,XU Weiya,YANG Chunhe,et al.Study on elastoplastic constitutive model of rock with statistical damage [J].Chinese Journal of Rock Mechanics and Engineering,2004 ,23 (Sup1) :4285-4291.(in Chinese))
[17] TERZAGHI K.The shearing resistance of saturated soils and the angle between the planes of shear[C]//Proceedings of the 1st international conference on soil mechanics and foundation engineering.Harvard University Press Cambridge,MA,1936,1: 54-56.
[18] LEMAITRE J.A continuous damage mechanics model for ductile fracture[J].Journal of Engineering Materials & Technology,1985,107: 83-89.
[19] FAIRHURST C E, HUDSON J A.Draft ISRM suggested method for the complete stress-strain curve for intact rock in uniaxial compression[J].International Journal of Rock Mechanics & Mining Science & Geomechanics Abstracts,1999,36(3):281-289.
Thestatisticaldamageconstitutivemodelofrocksanditsexperiment
WANGSusheng1,2,XUWeiya1,2,WANGWei1,2,WANGRubin1,2,XIANGZhipeng1,2
(1.KeyLaboratoryofMinistryofEducationforGeomechanicsandEmbankmentEngineering,HohaiUniversity,Nanjing210098,China; 2.InstituteofGeotechnicalEngineering,HohaiUniversity,Nanjing210098,China)
Based on the Mohr-Coulomb failure criterion and the hypothesis of the rock micro-unit strength subject to Weibull random distribution, a new statistical damage constitutive model is established by introducing the pore water pressure by means of the effective stress theory. The new model can consider the influences of both pore volume change and damage threshold. In addition, a novel micro-unit strength calculation method for the rock is proposed. In order to make the model parameters have definite physical meaning, the model parametersmandF0are determined by using the peak point strength in the stress strain curve. In this study, the conventional triaxial compression tests for sandstone are conducted to verify the rationality of the model, by which the damage evolution and porosity variation of the rock under different confining pressures are analyzed, and the effects of confining pressures on the model parameters are explored. The findings show that the model can well reflect the relationship between triaxial stress and strain of the rock.
rock mechanics;Mohr-Coulomb criterion; Weibull distribution; microcosmic element strength; statistical damage model
10.3876/j.issn.1000-1980.2017.05.014
2016-08-25
国家自然科学基金 (11172090)
王苏生(1989—),男,河南信阳人,博士研究生,主要从事岩石力学研究。E-mail:sushengwang1989@163.com
TU452
A
1000-1980(2017)05-0464-07

