基于分布式水文模型的山洪预警临界雨量计算
刘淑雅,江善虎,2,任立良,2,沈鸿仁,袁 飞,2,郑巍斐
(1.河海大学水文水资源学院,江苏 南京 210098; 2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)
基于分布式水文模型的山洪预警临界雨量计算
刘淑雅1,江善虎1,2,任立良1,2,沈鸿仁1,袁 飞1,2,郑巍斐1
(1.河海大学水文水资源学院,江苏 南京 210098; 2.河海大学水文水资源与水利工程科学国家重点实验室,江苏 南京 210098)
以抚河流域3个山丘小流域为例,采用分布式新安江模型对小流域暴雨洪水进行精细化模拟,利用率定后的分布式新安江模型进行临界雨量试算,得出各流域不同初始土壤含水量、不同预警时段组合条件下临界雨量。将计算所得临界雨量与实测暴雨洪水过程和设计暴雨进行比较验证,结果表明临界雨量计算结果较为合理,说明分布式新安江模型可应用于抚河流域山洪预警临界雨量确定,并为抚河流域山洪预警工作的开展提供参考方法。
临界雨量;新安江模型;土壤含水量;山洪预警;抚河流域
山洪灾害是指因降雨在山丘区引发的洪水及由山洪诱发的泥石流、滑坡等对国民经济和人民生命财产造成损失的灾害。我国山丘区面积大、人口多,山洪灾害往往会造成严重损失。因此,山洪灾害预警是我国山丘区防灾减灾的重要任务[1]。临界雨量法是用于判断山洪灾害发生与否的最为常用的方法之一[2-3]。一个流域或区域某一时段内降雨量达到或超过某一量级和强度时,该流域或区域将发生山溪洪水、泥石流、滑坡等山洪灾害,这个降雨量即为该流域或区域的临界雨量[4]。本文仅对将发生山溪洪水灾害的临界雨量进行计算,即分析可能发生山溪洪水山洪灾害时所需要的最小降水量。
针对临界雨量的确定,国内外提出了不同的研究思路。国外较为常用的是美国水文研究中心(HRC)研发的FFG(flash flood guidance)系统[5]。该方法最早提出推理公式法反推临界雨量,近几年得到进一步的发展,将FFG与分布式水文模型结合起来,形成基于网格的FFG[6]。目前FFG系统已被广泛应用于美国、韩国、中美洲、湄公河流域等[3, 7-8]。我国早期由于数据资料不完整、站网密度较低,多采用统计归纳法[9-12]。这类方法并不关注山洪灾害过程涉及到的物理机制,而是直接从降雨及山洪灾害数据推求临界雨量,方法简单,应用方便,对其他数据的需求相对较少,但精确度较低[13]。随着具有物理意义的水文模型在我国的发展和应用,临界雨量的推求逐步与水文模型结合起来。刘志雨等[14]提出了以GBHM模型为基础的动态临界雨量方法,即选出在洪峰达到警戒流量之前各时段的最小降雨量作为临界雨量,并在江西遂川江流域得到应用。叶金印[15]、陈瑜彬等[16]基于最小均方差准则,建立不同时间尺度的动态临界雨量判别函数,并结合历史资料对结果进行检验。李昌志等[17]分析了基于分布式水文模型的山洪预警临界雨量,该方法可以较为详细地分析流域各部分产汇流特征,有利于客观准确地模拟山丘区小流域洪水,使得临界雨量在预警指标分析中具有很好的应用前景。
目前我国临界雨量推求方法还存在未充分考虑前期影响雨量、雨强等因素的动态变化,对下垫面条件的描述精准度不高,时段固定单一,精度不高等问题。本文结合近期研究进展,选取抚河流域雨洪资料完备的3个典型山丘小流域,基于分布式新安江模型开展暴雨洪水的精细化模拟,提出基于分布式水文模拟的临界雨量确定方法,并结合实测资料和设计暴雨进行结果验证。
1 研究区概况
抚河流域属亚热带湿润季风气候区,多年平均气温为16.9~18.2 ℃,多年平均降水量为1 500~2 000 mm,地理位置位于江西省东部,主要支流有临水、盱江、东乡水、黎滩河等,贯穿抚州市中南部,注入鄱阳湖。抚河流域三面环山,降雨锋面、强度均易受到山体阻碍和抬升作用而加大,当土壤含水量达到饱和时,主要由黄壤和红壤组成的山区表土层土抗减小,在暴雨和重力作用下,容易引发山洪灾害[18]。
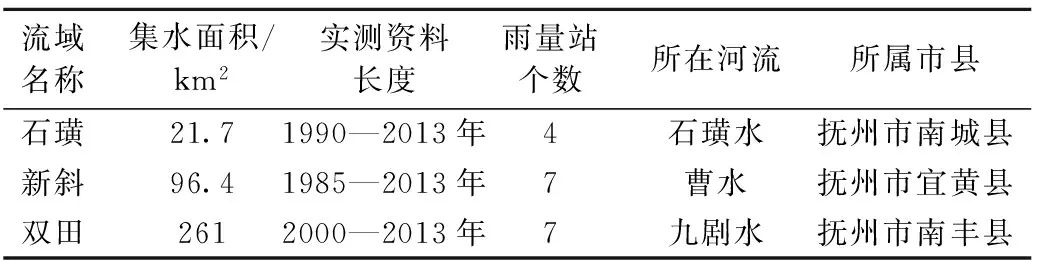
表1 抚河3个典型小流域基本情况
研究选取3个雨洪资料较完备的典型山丘小流域(石璜小流域、新斜小流域及双田小流域)进行流域暴雨洪水过程模拟以及临界雨量分析,各小流域基本情况见表1。
2 研 究 方 法
2.1基于分布式新安江模型的小流域洪水模拟
新安江模型是我国应用较广泛的流域水文模型之一,模型结构简单,参数少且大多数有明确的物理意义,与流域自然条件关系紧密、区域规律性强,容易率定。本文采用栅格化的分布式新安江模型(GRIDXAJ)进行暴雨洪水过程模拟。GRIDXAJ模型以流域内每个DEM栅格作为计算单元,并假设栅格单元内的降雨、地貌特征、土壤类型以及植被覆盖等下垫面条件空间分布均匀,只考虑各要素在不同栅格间的变异性[19-22]。
在抚河3个小流域,基于SRTM-90m分辨率的DEM数据,运用ArcGIS中Arc-Hydro模块计算各典型小流域的流域边界、栅格水流方向和汇流演算次序,提取各小流域的IGBP土地覆盖信息和土壤质地信息,以90 m空间分辨率的栅格作为GRIDXAJ模型产汇流计算的基本单元;根据小流域降水、流量数据获取情况,重点模拟2000年以来各小流域的日径流及次洪过程,其中前2/3模拟期为率定期,后1/3模拟期为验证期;选取率定好的GRIDXAJ模型产汇流参数,为临界雨量试算提供模型基础。
2.2临界雨量确定方法
2.2.1 预警时段拟定方法
控制断面上游的集水面积大小、流域降雨强度、流域的形状及其下垫面因子等都会对预警时段产生影响。一般说来,流域越大,预警时段越长;流域比降越大,预警时段越短。流域汇流时间理论上为预警的最长时段,但实际预警中会做适当延长。选取各小流域典型暴雨-洪水过程分析流域汇流时间,考虑流域各处流速变化不大,流域滞时大体相当于流域平均汇流时间,因此近似将流域最大雨强出现时刻到洪峰出现时刻之间的时间视为流域汇流时间,依据汇流时间并做适当调整确定预警时间。
2.2.2 预警流量确定方法
由于未收集到研究流域的山洪灾害调查断面数据,论文根据水文站大断面图确定上滩水位,采用水文站实测水位流量关系,查算上滩水位对应的流量,并结合水文站不同频率设计洪水,综合确定预警流量。
2.2.3 土壤含水量确定方法
采用美国农业部(USDA)水土保持局提出的SCS-CN法计算各小流域蓄水容量[23],比照江西省暴雨洪水查算手册推荐的流域蓄水容量,综合确定各小流域蓄水容量值。
2.2.4 临界雨量试算
首先为临界雨量假定一个初始值,根据雨型的时程分配对该值进行分配,从而能够得到降雨过程,将其作为模型的初始降水输入,模拟得到相应的径流过程。其次,针对得到的径流过程进行分析,如果其洪峰流量接近预警流量值,则假定的初值就是该预警时段的临界雨量;反之,如果与预警流量值相差较大,则重新假定初值,计算模型的初始降水输入,并进行模拟、比较;如此反复地进行试算,直到计算所得的洪峰流量接近预警流量值,则该值为临界雨量。
3 结 果 分 析
3.1抚河流域洪水模拟——以石璜站为例
3.1.1 日模拟结果
采用GRIDXAJ模型模拟石璜站1990—2013年日径流过程,率定期为1990—2004年,验证期为2005—2013年。GRIDXAJ模型模拟率定期年径流深相对误差为1.89%,确定性系数为0.73;验证期年径流深相对误差为-5.11%,确定性系数为0.72。由图1可知,GRIDXAJ模型模拟的石璜站日流量过程与实测日流量基本一致,表明GRIDXAJ模型能够基本再现石璜站的历史日流量过程。

图1 石璜站验证期1996年、率定期2012年日流量过程模拟结果Fig.1 Modeling results of daily flow during calibration period in 1996 and validation period in 2012 in Shi Huang Station
3.1.2 次洪结果
采用GRIDXAJ模型模拟石璜站2001—2013年期间15场次洪过程,其中率定期10场次洪,验证期5场次洪。表2统计了GRIDXAJ模型模拟石璜站洪水过程的精度。率定期各场次洪的径流深相对误差均在±10%以内,各场次洪的峰现时差均在±2 h以内,次洪模拟平均合格率为96.7%,确定性系数均值为0.76。验证期各场次洪径流深相对误差均在±3%以内,洪峰流量相对误差均在±30%以内,各场次洪的峰现时差均在±2 h以内,模拟结果均为合格,确定性系数均值为0.71。从模拟结果可以看出,GRIDXAJ模型在石璜站进行洪水模拟结果较好,具有较好适用性。
图2展示了石璜站率定期和验证期的场次洪水过程,可以看出,在率定期和验证期,GRIDXAJ模型均能较准确模拟石璜站次洪过程。
总体上,GRIDXAJ模型能较准确地模拟所选典型小流域的日径流过程和次洪过程。日径流过程模拟中,率定期及验证期的相对误差均在±5%左右,确定性系数均高于0.6。次洪过程模拟中,新斜及双田小流域的模拟平均合格率达到100%,确定性系数也均高于0.8,石璜小流域的模拟平均合格率为96.7%,率定期及验证期的确定性系数均高于0.7,各流域模拟洪水过程合格率统计见表3。

表2 GRIDXAJ模型模拟石璜站洪水过程精度统计
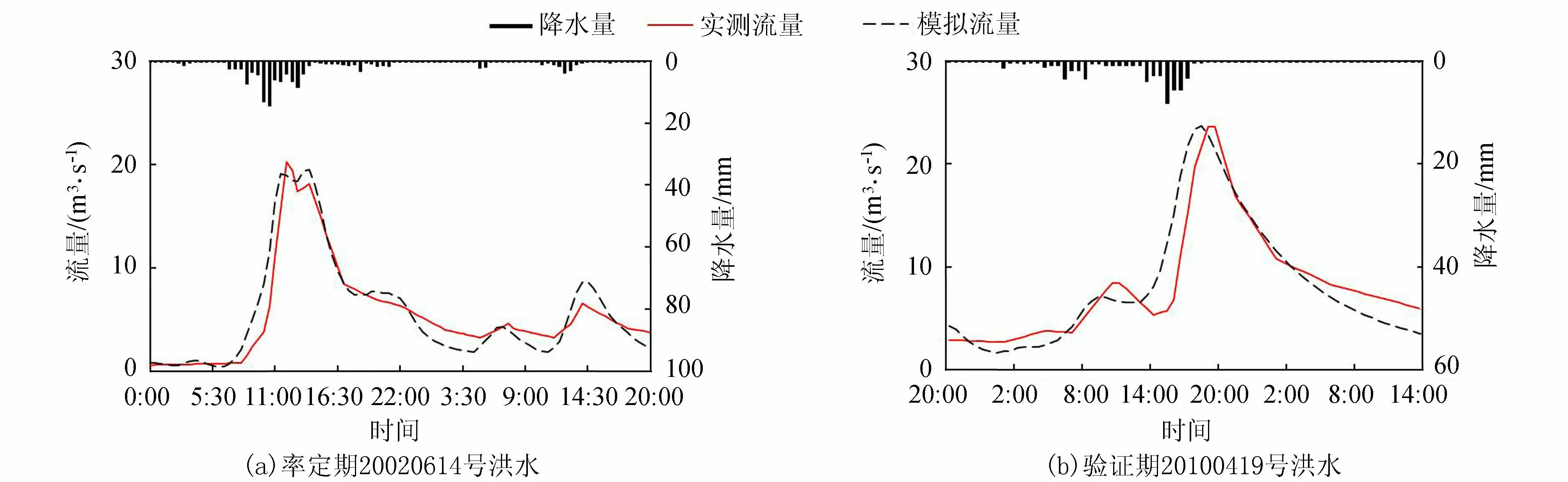
图2 石璜站率定期20020614号洪水过程和验证期20100419号洪水过程Fig.2 Simulated hydrograph of GRIDXAJ for the flood 20020614 and 20100419
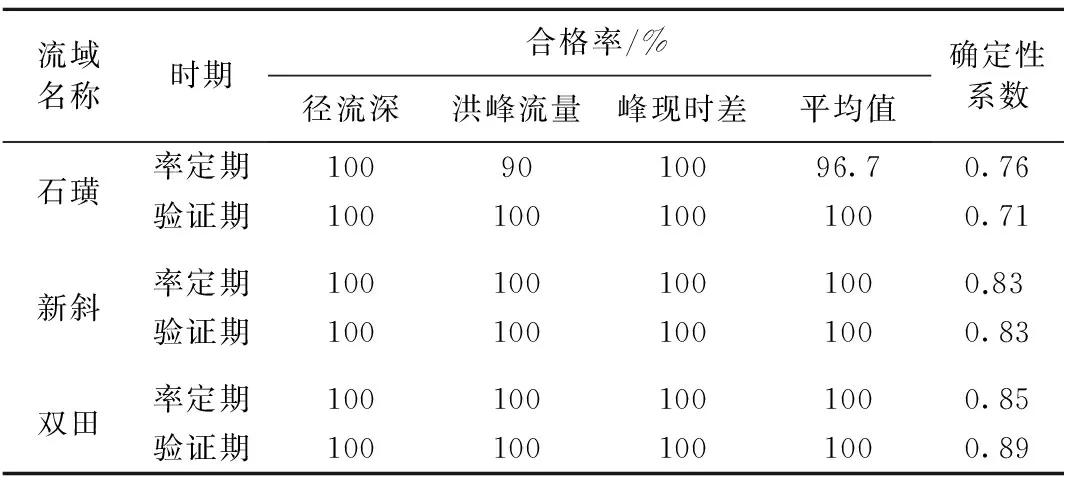
流域名称时期合格率/%径流深洪峰流量峰现时差平均值确定性系数石璜新斜双田率定期1009010096.70.76验证期1001001001000.71率定期1001001001000.83验证期1001001001000.83率定期1001001001000.85验证期1001001001000.89
各流域次洪过程的模拟径流深和洪峰流量与实测比较结果显示:石璜、新站、双田站模拟径流深与实测径流深的相关系数R均为0.99,洪峰洪量与实测洪峰洪量的R也均为0.99,说明GRIDXAJ模型均能较准确地模拟典型小流域次洪径流深和洪峰流量。
3.2临界雨量计算关键参数确定
3.2.1 预警时段拟定
选择典型暴雨进行流域汇流时间的近似计算,根据典型暴雨洪水过程分析各小流域的雨洪响应历时。石璜、新斜和双田流域的暴雨洪水响应时间近似分别为2 h、3 h和6 h。根据《山洪灾害分析评价技术要求》,最长预警时段应选择流域汇流时间,为了分析不同流域不同预警时段预警指标的变化规律,研究将预警时段统一确定为1 h、3 h、6h这3个时段。
3.2.2 预警流量确定
以石璜站为例,查找石璜水文站控制断面图,确定其上滩水位为94.79 m,通过石璜水文站水位-流量关系曲线,得出上滩水位对应的流量为26.5 m3/s,同理可得出新斜、双田上滩流量为130 m3/s和370 m3/s。而基于流量推求的石璜、新斜和双田的5年一遇设计洪峰流量为38.4 m3/s、148 m3/s和336 m3/s,经比较查算发现上滩流量和5年一遇设计洪峰流量较为一致,为了各流域计算临界雨量结果的可比性,统一确定这3个流域的警戒流量为5年一遇设计洪峰流量。
3.2.3 土壤含水量计算
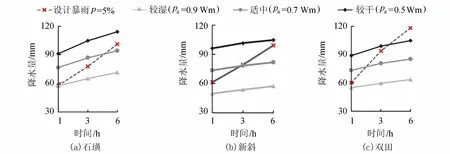
根据《山洪灾害分析评价技术要求》,应选择不同情况下的土壤初始含水量进行预警指标分析。将土壤湿度分为较干(土壤初始含水量Pa≤0.5Wm)、适中(0.5Wm 3.2.4 试算雨型 表4 基于GRIDXAJ模型推求的3个流域临界雨量 采用的预警时段为1 h、3 h和6 h,在进行临界雨量试算时,按照Δ=30 min的时间步长,确定相应的降雨过程序列,作为模型的初始输入条件。参照《江西省暴雨洪水查算手册》2010版中以1 h为时段的雨型分配为依据,作为3 h、6 h临界雨量的雨型分配标准。 3.3临界雨量计算结果 表4为3个典型流域基于GRIDXAJ模型计算的临界雨量值,可以看出:总体上3个流域不同情景下临界雨量存在差异,但递变规律相似:临界雨量随土壤湿度增加而减小、随预警时段增长而增大的特点。不同时段的临界雨量存在一定的波动,相同时段的临界雨量变幅也较为明显,主要原因是雨型分配差异导致的降水均化对水文模型影响较大,使得同一警戒流量对应的不同时段临界雨量梯度加大;此外,GRIDXAJ模型考虑了不同流域下垫面特性,因此同种情景、相同预警时段的临界雨量变动幅度较大。 由于抚河流域缺少洪水调查资料,无法采用误报率进行评估验证,因此采用与洪峰相近的实测次洪资料以及5年一遇的设计暴雨进行验证分析。 4.1与实测资料比较 将3个小流域的计算结果与实测资料进行比较,验证使用GRIDXAJ模型计算临界雨量的合理性。以新斜为例分析:通过查找新斜水文站长系列场次洪水资料,选取洪峰流量接近预警流量Q=148 m3/s的一场次洪,即2010年6月20日16:30达到的洪峰166 m3/s,选择预警时段为6 h且前期较湿情景下临界雨量雨型作为输入模拟洪水过程和实测洪水过程,发现二者洪峰值较为吻合,实测最大6 h降雨为71 mm,而模型试算湿润情景下6 h临界雨量为57.3 mm,由于实测洪峰流量更大,所以最大6 h雨量二者有所偏差亦为合理情况。同理验证石璜、双田小流域,均与实测资料均较为接近,结果如图3和表5。 图3 3个小流域临界雨量验证结果Fig.3 Verification results of the critical rainfall in three watersheds 流域名称洪号预警时段/h警戒流量/(m3·s-1)实测流量/(m3·s-1)实测降水量/mm临界雨量/mm石璜19980622338.437.958.564.7新斜201006206148.0166.071.069.4双田200506206336.0341.065.763.3 4.2与设计暴雨比较 设计暴雨采用实测系列频率计算法,根据抚河3个小流域年最大1 h、3 h和6 h点暴雨系列,经频率分析计算得到的设计点暴雨。将各流域计算出的不同情景、不同时段的临界雨量值与5年一遇设计暴雨值进行比较,由图4可以发现除双田流域5年一遇最大6 h设计暴雨高于较干情景下的临界雨量值之外,石璜、新斜、双田3个流域的5年一遇设计暴雨值均包含在3种初始土湿情景下各时段临界雨量范围内,说明临界雨量计算值整体符合历史暴雨的重现期范围,双田流域出现偏差可能原因是实测资料中出现前期土湿较干情景的频率较高,因此最大6 h的设计暴雨前期情景可能更为干旱,进一步研究时可以将情景划分更细一些,如干旱情景从0.1Wm开始计算;此外在相同初始土湿情景下,随着时段从1 h到3 h、6 h,各个小流域临界雨量和设计暴雨的增幅不尽相同,初步分析可能与下垫面以及降雨强度有关,未来可做进一步分析研究;随着时段的增长,设计暴雨与临界雨量的相似情景由较湿到较干,说明预警时段较短时,设计暴雨值与较湿情景临界雨量值较为接近,因此在无资料地区进行山洪预警临界雨量计算时,短时段的设计暴雨值可以为临界雨量的推算提供参考。 图4 3个小流域临界雨量与设计暴雨比较Fig.4 Comparison between the critical rainfall and the design storm in three watersheds 临界雨量是山洪预警的重要指标,能够快速、直接地为是否发布山洪灾害预警提供依据。本文基于分布式新安江模型,充分考虑气候因子以及下垫面因子的空间不均匀性,采用精细化方案对暴雨洪水过程进行模拟;结合不同预警时段、不同初始土湿组合条件,基于分布式水文新安江模型试算了不同流域临界雨量。采用暴雨洪水资料及设计暴雨资料验证临界雨量计算结果较为可靠。论文研究结果为抚河流域山洪灾害预警提供了指导,也为我国小流域山洪预警工作提供了方法和建议。 [ 1 ] 刘志雨. 山洪预警预报技术研究与应用[J]. 中国防汛抗旱, 2012,22(2):41-45, 50.(LIU Zhiyu. The study and application of mountainous flood warning and prediction technology[J]. China Flood & Drought Management, 2012,22(2):41-45, 50.(in Chinese)) [ 2 ] GEORGAKAKOS K P. Analytical results for operational flash flood guidance[J]. Journal of Hydrology, 2006,317(1/2):81-103. [ 3 ] CARPENTER T M, SPERFSLAGE J A, GEORGAKAKOS K P, et al. National threshold runoff estimation utilizing GIS in support of operational flash flood warning systems[J]. Journal of Hydrology, 1999,224(1/2):21-44. [ 4 ] 全国山洪灾害防治规划领导小组办公室. 山洪灾害临界雨量分析计算细则(2003版)[EB/OL].[2016-09-19]. https://wenku.baidu.com/view/5412e4d850e2524de5187e0b.html [ 5 ] HAPUARACHCHI H A P, WANG Q J, PAGANO T C. A review of advances in flash flood forecasting[J]. Hydrological Processes, 2011,25(18):2771-2784. [ 6 ] NORBIATO D, BORGA M, DINALE R. Flash flood warning in ungauged basins by use of the flash flood guidance and model-based runoff thresholds[J]. Meteorological Applications, 2009,16(1):65-75. [ 7 ] GAUME E, BAIN V, BERNARDARA P, et al. A compilation of data on European flash floods[J]. Journal of Hydrology, 2009,367(1/2):70-78. [ 8 ] NORBIATO D, BORGA M, DEGLI E S, et al. Flash flood warning based on rainfall thresholds and soil moisture conditions: an assessment for gauged and ungauged basins[J]. Journal of Hydrology, 2008, 362 (3/4):274-290. [ 9 ] 江锦红, 邵利萍. 基于降雨观测资料的山洪预警标准[J]. 水利学报, 2010,41(4):458-463.(JIANG Jinhong, SHAO Liping. Standard of mountain flood warning based on the precipitation observation data[J].Journal of Hydraulic Engineering, 2010,41(4):458-463.(in Chinese)) [10] 王鑫, 曹志先, 谈广鸣. 暴雨山洪水动力学模型及初步应用[J]. 武汉大学学报(工学版), 2009,42(4):413-416.(WANG Xin, CAO Zhixian, TAN Guangming. Shallow water hydrodynamic modelling of rainfall-induced flash flooding[J]. Engineering Journal of Wuhan University, 2009,42(4):413-416.(in Chinese)) [11] 徐少军, 江炎生, 毛北平, 等. 基于降雨径流关系曲线插值法的山洪临界雨量计算[J]. 中国防汛抗旱, 2015,25(6):30-35.(XU Shaojun, JIANG Yansheng, MAO Beiping, et al. Method of flash flood rainfall indicator determination based on rainfall-runoff charts[J]. China Flood & Drought Management, 2015,25(6):30-35.(in Chinese)) [12] 陈桂亚, 袁雅鸣. 山洪灾害临界雨量分析计算方法研究[J]. 人民长江, 2005,36(12):40-43.(CHEN Guiya, YUAN Yaming. Research on analysis and computation method of critical precipitation amount of torrential flood[J]. Yangtze River, 2005,36(12):40-43.(in Chinese)) [13] 程卫帅. 山洪灾害临界雨量研究综述[J]. 水科学进展, 2013,24(6):901-908.(CHENG Weishuai. A review of rainfall thresholds for triggering flash floods[J]. Advances in Water Science, 2013,24(6):901-908.(in Chinese)) [14] 刘志雨, 杨大文, 胡健伟. 基于动态临界雨量的中小河流山洪预警方法及其应用[J]. 北京师范大学学报(自然科学版), 2010,46(3):317-321.(LIU Zhiyu, YANG Dawen, HU Jianwei. Dynamic critical rain-fall-based torrential flood early warning for medium-small rivers[J].Journal of Beijing Normal University(Natural Science),2010,46(3):317-321.(in Chinese)) [15] 叶金印. 基于动态临界雨量的山洪预警方法研究与应用[J]. 气象, 2014,40(1):101-107.(YE Jinyin. Research and application of flash flood early warning method based on dynamic critical precipitation [J]. Meteorological Monthly, 2014,40(1):101-107.(in Chinese)) [16] 陈瑜彬, 杨文发, 许银山. 不同土壤含水量的动态临界雨量拟定方法研究[J]. 人民长江, 2015(12):21-26.(CHEN Yubin, YANG Wenfa, XU Yinshan. Study of dynamic critical precipitation drafted method under different soil moisture content level[J]. Yangtze River, 2015(12):21-26.(in Chinese)) [17] 李昌志, 郭良, 刘昌军, 等. 基于分布式水文模型的山洪预警临界雨量分析:以涔水南支小流域为例[J]. 中国防汛抗旱, 2015,25(1):70-76.(LI Changzhi, GUO Liang, LIU Changjun, et al. Flash flood early-warning indicators based on distributed hydrological model:a case study in south branch of Censhui Watershed[J]. China Flood & Drought Management, 2015,25(1):70-76.(in Chinese)) [18] 饶印泉. 抚州市山洪灾害特性分析[J]. 科技广场, 2007(7):254-256.(RAO Yinquan. Torrential flood disaster characteristic property analyses Fuzhou City[J]. Science Mosaic, 2007(7):254-256.(in Chinese)) [19] 姚成, 纪益秋, 李致家, 等. 栅格型新安江模型的参数估计及应用[J]. 河海大学学报(自然科学版), 2012,40(1):42-47.(YAO Cheng, JI Yiqiu, LI Zhijia, et al. Parameter estimation and application of grid-based Xin’anjiang model[J]. Journal of Hohai University(Natural Sciences), 2012,40(1):42-47.(in Chinese)) [20] 赵人俊, 王佩兰, 胡凤彬. 新安江模型的根据及模型参数与自然条件的关系[J]. 河海大学学报(自然科学版), 1992,20(1):52-59.(ZHAO Renjun, WANG Peilan, HU Fengbin. Relations between parameter values and corresponding natural conditions of Xinanjiang model[J]. Journal of Hohai University(Natural Sciences), 1992,20(1):52-59.(in Chinese)) [21] 刘金涛, 宋慧卿, 张行南, 等. 新安江模型理论研究的进展与探讨[J]. 水文, 2014,34(1):1-6.(LIU Jintao, SONG Huiqing, ZHANG Xingnan, et al. A discussion on advances in theories of Xin’anjiang model[J]. Journal of China Hydrology, 2014,34(1):1-6.(in Chinese)) [22] 王莉莉, 李致家, 包红军. 基于DEM栅格的水文模型在沂河流域的应用[J].水利学报, 2008, 39(增刊1):417-422.(WANG Lili, LI Zhijia, BAO Hongjun. Application of hydrological models based on DEM in the Yihe Basin[J]. Journal of Hydraulic Engineering, 2008, 39(Sup1): 417-422. (in Chinese)) [23] SHADEED S. Application of GIS-based SCS-CN method in West Bank Catchments, Palestine[J]. Water Science and Engineering, 2010,3(1):1-13. Calculationofcriticalrainfallforearly-warningofmountainfloodbasedondistributedhydrologicalmodel LIUShuya1,JIANGShanhu1,2,RENLiliang1,2,SHENHongren1,YUANFei1,2,ZHENGWeifei1 (1.CollegeofHydrologyandWaterResources,HohaiUniversity,Nanjing210098,China;2.SateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,HohaiUniversity,Nanjing210098,China) In this paper, a case study is performed on three small hill watersheds in Fuhe River Basin, where their storm flood process was simulated elaborately by using distributed Xin’anjiang model. The critical rainfall of each watershed is calculated by means of the verified Xin’anjiang model, so the different initial soil moisture of each watershed and the critical rainfall under different combinations of warning intervals can be determined. The calculated result of critical rainfall is demonstrated to be reasonable by comparing and validating with the measured storm flood data and storm design, which suggests that the distributed Xin’anjiang model can be used to determine the critical rainfall for early-warning of mountain flood in Fuhe River Basin. Besides, it provides a reference method for the early warning of mountain flood in Fuhe River Basin. critical rainfall; Xin’anjiang model; soil moisture; mountain flood warning; Fuhe River Basin 10.3876/j.issn.1000-1980.2017.05.002 2016-09-19 国家重点研发计划(2016YFA601504);2016山洪灾害防治项目(SHZH-IWHR-80) 刘淑雅(1990—),女,山东济南人,博士研究生,主要从事流域水文模型及洪水预报预警研究。E-mail: annmail@126.com P426.616 A 1000-1980(2017)05-0384-07
4 验 证 分 析


5 结 语

