动态聚类最近邻法在湖库蓝藻水华预测中的应用

白晓哲, 张慧妍, 王小艺, 王 立, 许继平, 于家斌

(北京工商大学 计算机与信息工程学院 食品安全大数据技术北京市重点实验室, 北京 100048)

动态聚类最近邻法在湖库蓝藻水华预测中的应用

白晓哲, 张慧妍, 王小艺, 王 立, 许继平, 于家斌

(北京工商大学计算机与信息工程学院食品安全大数据技术北京市重点实验室,北京100048)

[目的] 探索湖库蓝藻水华的有效预测方法，为水环境污染防治关键问题的解决提供科学依据。 [方法] 结合蓝藻水华演化中表现出的混沌类随机特点，提出一种基于有效性函数优化的动态聚类算法，以实现蓝藻水华动态、小范围近邻优化预测的目的。首先，基于动态聚类算法对监测数据进行典型类的客观划分，为后续有效减小搜索空间，提高预测精度奠定基础；而后采用粒子群算法优化得到各类的最佳近邻个数，以确定参与回归建模的观测值数量；最后依据最近邻观测数据建立动态回归预测模型。 [结果] 采用太湖金墅监测站点2011年叶绿素a浓度测定值进行建模，之后对2012年叶绿素a浓度进行短期预测。新建模型的预测值与实际值运行趋势一致，且相对误差为12.02%，而基于传统聚类线性回归算法的相对误差为15.21%，基于BP神经网络预测算法的相对误差为19.51%，相空间重构算法的相对误差为38.42%。 [结论] 算例结果表明该方法的预测精度相对较高，证明了所提优化预测方法的可行性与有效性。

蓝藻水华; 动态聚类; 最近邻法; 预测

文献参数： 白晓哲, 张慧妍, 王小艺, 等.动态聚类最近邻法在湖库蓝藻水华预测中的应用[J].水土保持通报，2017,37(4)：161-165.DOI:10.13961/j.cnki.stbctb.2017.04.027； Bai Xiaozhe, Zhang Huiyan, Wang Xiaoyi, et al. Dynamic clustering based on nearest neighbors for predicting of cyanobacteria bloom in lakes and reservoirs[J]. Bulletin of Soil and Water Conservation, 2017,37(4)：161-165.DOI:10.13961/j.cnki.stbctb.2017.04.027

随着中国工农业的迅猛发展以及城市化进程的加快，水体富营养化问题日益突出。水体富营养化是指水体接纳过量的氮、磷等营养性物质，使得水体中藻类以及其他水生生物异常过度繁殖，出现水体溶解氧含量下降，透明度降低，动植物大批死亡，造成水质恶化，使水域生态和水功能受到阻碍和破坏，严重的甚至发生水华，给湖泊水环境及其生态系统带来严重后果[1]。水体富营养污染诱发水华暴发是一个多因素耦合、多维度消涨和具有内在强非线性耗散结构的复杂动力学体系[2]。国内学者王海云[3]对三峡库区支流水华暴发的污染演变效应进行了分析，发现在水域、水文、时间、藻类组成、浮游生物指标等因素上存在着大量的变化不明显、关系模糊、突变、约束、开放、自组织的混沌非线性行为效应，演变过程轨迹符合非线性行为效应特征；王小艺[4]在对湖库蓝藻水华生成过程进行机理研究的基础上，对其进行混沌特性判断，结合复杂网络的统计特征参数，提出一种新的蓝藻水华预测方法。由于混沌理论为具有随机性、动态性的非线性复杂系统提供了可行的研究途径，并且已经在一些领域得到应用[5-8]。

目前，有关混沌时间序列的预测方法主要有全局预测法和局域预测法，其基本思路都是根据观测数据，重构相空间，然后采用适当的建模方法在相空间中找到一个局部线性模型逼近系统动态特性，实现一定时段内的短时预测，但它们有一定的局限性：一是模型阶数较低，导致估计精度不高、鲁棒性较差；二是需要的基础知识较多、数据量及计算量较大、不便于理解。本文基于运行工作点局部线性化思想，提出利用有效性函数依据研究对象的数据特征动态划分典型数据进行聚类，而后基于最近邻相似原则，通过粒子群算法优化确定参与建模的最佳近邻数量，最后应用回归算法构建预测模型，有效地利用了邻域内的多个历史信息。最后针对太湖金墅监测站点的叶绿素a浓度实测数据进行研究，结果表明该算法简洁、有效，具有较好的预测精度。

1 基本原理及算法改进

传统的单变量混沌时间序列预测是基于Packard等人提出的相空间重构方法[9]，其中关键参数的选取存在一定的不确定性与不一致性。

1.1 基于动态聚类的混沌时间序列模型

聚类是一种无监督学习过程。K-means聚类是基于距离的聚类算法，具有算法简单快速、适于处理大数据集等优点，是聚类分析中使用最为广泛的算法之一。

目前K-means聚类在应用中存在两个需要解决的问题：一是最佳聚类数的确定；二是K-means聚类中边界位置有用信息的处理。这两个问题的有效处理，对于后续预测精度的提高具有重要意义。为此，本文提出从以下两个方面对传统K-means聚类算法进行改进。

1.1.1 建立聚类有效性指标，确定最佳聚类数 构建有效性指标，指标函数取值最优时对应的聚类结果即为最优聚类划分。研究[10-11]表明，没有一种有效性指标能够在任何情况下都具有普遍适用性，目前常用的4种聚类有效性指标为Calinski-Harabasz(CH)指标[12]、Hartigan(Ht)指标[13]、Homogeneity-Separation(HS)指标[14]、Krzanowski-Lai(KL)指标[15]。本文基于前期对叶绿素a浓度预测研究经验，提出一种新的聚类有效性指标，即用聚类结果分布的自然属性来评价类内紧密性与类间分离性。

(1)

式中：Dwc(c)——聚类数为c时的类内距离；c——聚类个数;nw——第w(w=1,2,…,c)个子类的样本数目;xnw,i,xnw,j——含有nw个样本的子类中第i个样本和第j个样本，且i,j=1,2,…,nw。

(2) 类间距离。将两个聚类中心点之间的欧式距离定义为2个类的类间距离。类间距离公式为:

(2)

式中：Dbc(c)——聚类数为c时的类间距离；cu,cv——第u个聚类中心和第v个聚类中心, 且u,v=1,2,…,c。

(3)

式中：Coq——聚类数为c时的聚类综合质量；ε,p,q——平衡聚类类内距离与类间距离的权值，一般情况下p,q>0，0<ε<1。为了简化计算，取p=1，q=1；若类内距离的值较小，而类间距离的值较大，为了避免较大的类间距离对较小的类内距离的削弱作用，可增大类内距离的权值，本文中针对叶绿素a浓度的数据分布特点取ε=0.7。显然，聚类综合质量越大，表明聚类划分效果越好。

1.1.2 确定聚类区域，提高样本搜索精度 本文提出一种新的确定聚类半径的方法，用于确定有效聚类区域，可提高类内样本搜索速度与精度。

聚类半径公式为：

(4)

式中：Cra——聚类半径；N——某子类的样本个数；yd——第d个样本，且(d=1,2,…,N)；C——聚类中心；Dd——第d个样本与聚类中心的距离。

迭代过程中需要不断重新划定聚类区域，用更新后的聚类半径分离出边界点。则此子类边界点集合为：

Bin={Dd│Dd>Cra}

(5)

总边界点集合为：

BIN={Bin1,Bin2,…,Binc}

(6)

式中：BIN——总边界点集合； Binc——第c个子类的边界点集合。

后续则可依据未知对象所属的子类与边界点的集合来确定该未知对象的搜索空间。

1.2 粒子群算法

在确定了最佳聚类划分后，希望通过采用相似性样本信息构建模型逼近预测值，在这个过程中选取样本点的个数是一项较困难的工作。粒子群优化算法(particle swarm optimization, PSO)是由Eberhart与Kennedy[16]根据鸟类捕食行为而发明的一种新的全局优化进化算法。本文采用粒子群算法利用群体中的个体样本对信息的共享，实现问题求解空间从无序到有序的演化过程，从而获得最优解。其中，粒子m的第b维速度与位置按如下公式进行更新：

(7)

(8)

这样，基于动态的局部优化思想，利用粒子群算法分别对划分后的聚类集合进行最佳邻居个数优化。最终确定在每类中选取 个最近邻样本数据建立回归模型进行预测应用。

回归模型为：

Y=βX+E=β0+β1X1+β2X2+…+βkXk+E

(9)

式中：k——粒子群优化得到的最佳邻居个数；βk——回归系数；E——随机误差。

1.3 模型预测

预测通常分为单步预测和多步预测，假设样本数为M，以单变量时间序列为研究对象的单步预测是指：利用t时刻前的M个观测值作为模型的输入数据，得到第t+1时刻的预测值；多步预测是指利用该M个样本不仅可以单步预测第t+1时刻的值，也可以预测第t+2，t+3，…,t+T个时刻的值，T——预测步长，即通过已知的样本集可以外推进行T步预测[17]。

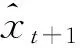
(10)

考虑本文所选水华数据具有混沌属性，采用间接多步预测可有效利用新信息逼近预测值，故本文应用了间接多步预测法进行叶绿素a浓度预测。

2 实例计算与分析

2.1 研究区概况与数据资料

太湖是中国第3大淡水湖，位于长江三角洲南部，面积2 338 km2，平均水深1.9 m，属于大型浅水湖泊。它不仅是旅游胜地，也是流域内大中城市的重要水源。近年来，随着太湖地区经济的迅速发展，环境保护和治理相对滞后，入湖主要河道和湖区的水质污染日益严重，特别是水体的富营养化，已经成为太湖水环境的主要问题。太湖的富营养化不仅制约着湖泊的可持续利用，而且直接影响到人民群众的身体健康，太湖蓝藻大规模爆发的条件短期内难以消除，太湖水华是个需要长期应对的问题，因此，建立水华预测系统，采取有力措施遏制水华迫在眉睫。本文将基于时间序列的优化动态聚类模型应用在具有混沌特性的湖库蓝藻水华表征因子——叶绿素a浓度的预测中。由于已证实蓝藻水华演化过程中具有混沌属性[4]，而混沌系统非常敏感的特性会因为一个微小扰动导致演化轨迹的巨大差异，因此，混沌系统不能进行长期预测；另一方面，混沌系统蕴含着一定的有序规律，轨迹发散但逃逸不出奇异吸引子的约束，这使得短期预测是可行的。基于此特性，本文中预测建模数据采用太湖金墅站点2011年1月至2011年12月每隔4 h采集的2 000组叶绿素a浓度数据，测试数据为2012年1月1日至2012年1月7日40组叶绿素a浓度数据。

2.2 最佳聚类数的确定

基于本文提出的有效性指标对预测建模数据进行优化聚类计算，得到聚类综合质量最大时对应的最佳聚类数为 。

对相同的数据集，采用上面提到的4种常用聚类有效性指标CH指标、Ht指标、HS指标、KL指标进行仿真试验，最后得到各个指标关于聚类数的变化曲线(图1)。CH指标、KL指标、HS指标将指标函数达到最大值时的聚类数作为最佳聚类数，Ht指标将指标函数值小于等于10的最小聚类数作为最佳聚类数。由图1可得，CH指标得到的最佳聚类数c=7；KL指标得到的最佳聚类数为c=6；HS指标得到的最佳聚类数为c=4；Ht指标得到的最佳聚类数为c=1。

图1 基于常用有效性指标曲线的聚类结果图

2.3 模型求解

对聚类划分的每个子类进行粒子群优化确定最佳近邻个数。粒子群算法的参数设置为：粒子维数为1维，迭代次数为100次，加速因子设置为2，因为线性权重比常数权重有更好的优化效果，这里采用线性递减权重；粒子群中的每一个粒子的位置值代表邻居个数的取值，粒子的变化范围设置为[10,100]；适应度函数为回归模型计算值与实际值的误差。优化结果确定最佳近邻个数为10。

这表明后续在已确定的典型类中可通过动态选取10个最近邻数据样本，建立回归预测模型。本文采用间接多步预测法进行之后40个时间点叶绿素a浓度预测以考察模型的有效性，得到预测值与实测值的对比图(图2)。仿真结果表明基于本文提出的优化动态聚类局部K最近邻法的预测值与表征水华形成的叶绿素a的实际值的运行趋势一致，并具有较好的预测精度。

图2 基于动态聚类算法的预测结果对比图

2.4 模型评价与分析

为了评价本模型的精度与所提有效性指标的有效性，针对同一数据集，分别采用相空间重构算法、基于BP神经网络的预测算法、基于传统聚类的回归算法对叶绿素a浓度进行对比预测，评价指标采用平均相对误差和最大相对误差。

相对误差的计算公式为：

(11)

式中：erz——相对误差； Acvz——第z组叶绿素a浓度实际值； Pcvz——第z组叶绿素a浓度预测值；

平均相对误差的计算公式为：

(12)

式中：erav——平均相对误差； g——预测长度。

最大相对误差的计算公式为：

ermax=max(│erz│)

(13)

式中：ermax——最大相对误差。

基于不同算法的预测值与实测值的对比图(图3)，预测误差详见表1。

由图3和表1可得，与相空间重构算法、基于BP神经网络预测算法和基于传统聚类的回归算法等相比，本文的预测方法精度相对较高；同时基于各种有效性指标的预测结果也验证了本文所提有效性指标——聚类综合质量的合理性与有效性。虽然采用HS指标得到的最佳聚类数与本文提出的聚类有效性指标结果相同，但是其计算方法难于理解、评估性和通用性不强，而本文提出的有效性指标计算方便、容易理解，具有很强的实用性与普适性。

图3 预测模型结果对比

预测方法 平均相对误差最大相对误差相空间重构算法0.38421.1000BP神经网络算法0.19510.4736传统聚类线性回归算法0.15210.5863动态聚类线性回归算法(基于Ht指标)0.14520.3957动态聚类线性回归算法(基于KL指标)0.12650.4753动态聚类线性回归算法(基于CH指标)0.13090.6370动态聚类线性回归算法(基于聚类综合质量)0.12020.3867

3 结 论

在考虑蓝藻水华表征因素叶绿素a浓度具有混沌特性的基础上，借鉴非线性系统局部动态建模的思想，提出一种基于聚类质量的有效性函数优化的动态聚类算法。其中优化动态聚类局部K最近邻方法中提出的有效性函数与一般常用的有效性函数相比能较好地划分叶绿素a浓度时间序列的典型类，高效地精简了建模与搜索范围；同时，采用粒子群算法优化确定类内的最近邻个数为后续非线性时间序列在典型区域内利用最近邻样本逼近预测值问题奠定了基础；最终基于太湖金墅站点叶绿素a浓度的预测分析结果表明，所提方法有效提高了具有混沌属性的叶绿素a浓度的非线性预测趋势与精度，且计算简便、可行性好，为非线性预测问题提供了很好的思路。

[1]GubelitYI,BerezinaNA.Thecausesandconsequencesofalgalblooms:TheCladophoraglomeratabloomandtheNevaEstuary(EasternBalticSea)[J].MarinePollutionBulletin, 2010,61(4/6):183-188.

[2] 陈兰荪.非线性生物动力系统[M].北京:科学出版社,1993.

[3] 王海云.三峡库区水华暴发演变的非线性行为效应研究[J].人民长江,2010,41(19):48-51.

[4] 王小艺.基于复杂网络的城市湖库藻类水华混沌时间序列预测方法:中国,201510128961.5[P].2015-03-24.

[5] 王一颉.多元混沌时间序列相关性分析及预测方法研究[D].辽宁 大连:大连理工大学,2008.

[6] 吕金虎.混沌时间序列分析及其应用[M].湖北 武汉:武汉大学出版社,2002.

[7]ZhangLichao,KongLiang,HanXiaodong,etal.Structuralclasspredictionofproteinusingnovelfeatureextractionmethodfromchaosgamerepresentationofpredictedsecondarystructure[J].JournalofTheoreticalBiology, 2016,400：1-10.

[8]YounesianD,NorouziH.ChaospredictioninnonlinearviscoelasticplatessubjectedtosubsonicflowandexternalloadusingextendedMelnikov’smethod[J].NonlinearDynamics, 2016,84(3):1163-1179.

[9] 韩敏,史志伟,郭伟.储备池状态空间重构与混沌时间序列预测[J].物理学报,2007,56(1):43-50.

[10] 周世兵.聚类分析中的最佳聚类数确定方法研究及应用[D].江苏 无锡:江南大学,2011.

[11] 王开军,李健,张军英,等.聚类分析中类数估计方法的试验比较[J].计算机工程,2008,34(9):198-199.

[12]CalinskiRB,HarabaszJ.Adendritemethodforclusteranalysis[J].CommunicationsinStatistics, 1974,3(1):1-27.

[13]HartiganJA,WongMA.AlgorithmAS136:AK-MeansClusteringAlgorithm[J].AppliedStatistics, 1979,28(1):100-108.

[14]ChenG,JaradatSA,BanerjeeN,etal.EvaluationandcomparisonofclusteringalgorithmsinanalyzingEScellgeneexpressiondata[J].StatisticaSinica, 2002,12(1):241-262.

[15]KrzanowskiWJ,LaiYT.Acriterionfordeterminingthenumberofgroupsinadatasetusingsum-of-squaresclustering[J].Biometrics, 1988,44(1):23-34.

[16] 姚德仓,宋松柏.设计洪水频率曲线的粒子群优化适线法研究[J].水土保持通报,2007,27(6):112-115.

[17] 殷礼胜,何怡刚,董学平,等.交通流量VNNTF神经网络模型多步预测研究[J].自动化学报,2014,40(9):2066-2072.

[18] 谢景新.非线性多步预测与优化方法及其在水文预报中的应用[D].辽宁 大连:大连理工大学,2006.

Dynamic Clustering Based on Nearest Neighbors for Predicting of Cyanobacteria Bloom in Lakes and Reservoirs

BAI Xiaozhe, ZHANG Huiyan, WANG Xiaoyi, WANG Li, XU Jiping, YU Jiabin

(Beijing Key Laboratory of Big Data Technology for Food Safety, College of Computer and Information Engineering, Beijing Technology and Business University, Beijing 100048, China)

[Objective] It is one of the key basic issue in the prevention and control of water environment by exploring effective prediction methods about cyanobacteria bloom in lakes and reservoirs. [Methods] Combined with the class random characteristic showed in the chaotic evolution of cyanobacteria bloom, this paper proposed a dynamic clustering algorithm based on the optimization of validity functions to achieve the optimal cluster number of cyanobacteria bloom and small-scale neighborhood optimal prediction. First of all, monitoring data were classified objectively by the proposed dynamic clustering algorithm to reduce effectively the search space and to improve the prediction accuracy. Then the optimal number of neighbors for all kinds was obtained using the particle swarm optimization algorithm, which was used to determine the number of participating in the local regressive algorithm. Finally, a dynamic regressive prediction model was established. [Results] The model established using the concentration data of chlorophyll a at the Jinshu monitoring site of Taihu Lake in 2011 was used to model and predict short-term variation of it in 2012. The predicted value of the model was consistent with the actual trend and the relative error was 12.02%, and was smaller than the ones predicted by other models, such as linear regression algorithm based on traditional clustering, BP neural network , and phase space reconstruction algorithm, whose relative errors were 15.21%, 19.51% and 38.42%. [Conclusion] Numerical results showed that the prediction accuracy of this method was relatively high, hence the feasibility and effectiveness of the optimization prediction method proposed were proved.

cyanobacteriabloom;dynamicclustering;nearestneighbormethod;prediction

B

： 1000-288X(2017)04-0161-05

： TP14， X524

2016-10-22

：2016-11-08

北京市属高校创新能力提升计划项目“北京河湖水环境监测与智能管理物联网应用平台”(PXM2014_014213_000033)； 北京市教委科技重点项目(KZ201510011011)； 北京市属高校青年拔尖人才培育计划(CIT&TCD201404031)

白晓哲(1993—),女(汉族),河北省邢台市人,硕士研究生,研究方向为蓝藻水华预测。E-mail:15031269259@163.com。

张慧妍(1973—),女(汉族),黑龙江省齐齐哈尔市人,博士,副教授,主要从事水质监测、数据建模、分类与预测方面的研究。E-mail:zhanghuiyan369@126.com。