音叉受迫振动的干涉测量

屈 帅，王艺蓉，白在桥

(北京师范大学 物理学系，北京 100875)

音叉受迫振动的干涉测量

屈 帅，王艺蓉，白在桥

(北京师范大学 物理学系，北京 100875)

通过干涉测量法得到音叉振动的幅频特性曲线，同时测量位移振幅和速度振幅. 实验中使用高品质因子音叉，激励信号的电压也降到了mV量级，既可以让音叉经过较长时间消除暂态过程，又可以减缓音叉由于长时间激励所带来的升温现象. 使用干涉测量法测量音叉受迫振动振幅，并给出2种数据处理方式. 该方法具有驱动功率小，测量精度高，直接测量位移量，同时测量两方面信号的优点.

音叉；高品质因子；幅频特性；小波分析；迈克耳孙干涉法

音叉是典型的振动系统，其二臂对称、振动相反，而中心杆处于振动的节点位置，净受力为零而不振动，其固有频率可因其质量和音叉臂长短、粗细而不同. 音叉广泛应用于多个行业，如用于生产标准的“纯音”、鉴别耳聋的性质、用于检测液位的传感器、用于检测液体密度的传感器以及计时器等[1].

通过线圈法测量音叉所得到的幅频特性曲线反映的是音叉速度振幅的大小，不能得到音叉位移振幅的大小. 由于音叉是铁制的，存在磁滞现象，并且接收线圈难以避免收到感应自激发线圈的信号. 在实验过程中，即使固定音叉，接收线圈仍然能够收到信号,且距离越近，感生信号越强.

通过麦克风法测量音叉幅频特性曲线(图1)反映的是音叉位移振幅的大小. 由于选用的是电容式麦克风，还可以避免接收到互感信号. 但由于音叉发声过小，容易受到环境噪声干扰，还会接收到环境噪声. 作者通过LabVIEW编程滤去环境噪声，结果还是不太理想，而且会有阶梯状的部分.

文献[2]中使用接收线圈和压电换能片同时测量音叉振动时的速度振幅和位移振幅，讨论“速度共振”与“位移共振”的相同与不同之处. 作者借鉴了文献中同时测量速度振幅与位移振幅的思想，通过迈克耳孙干涉装置来测量音叉速度振幅与位移振幅，并绘制相应的幅频特性曲线. 测量结果真实反映音叉位移振幅，精度可以达到μm量级.

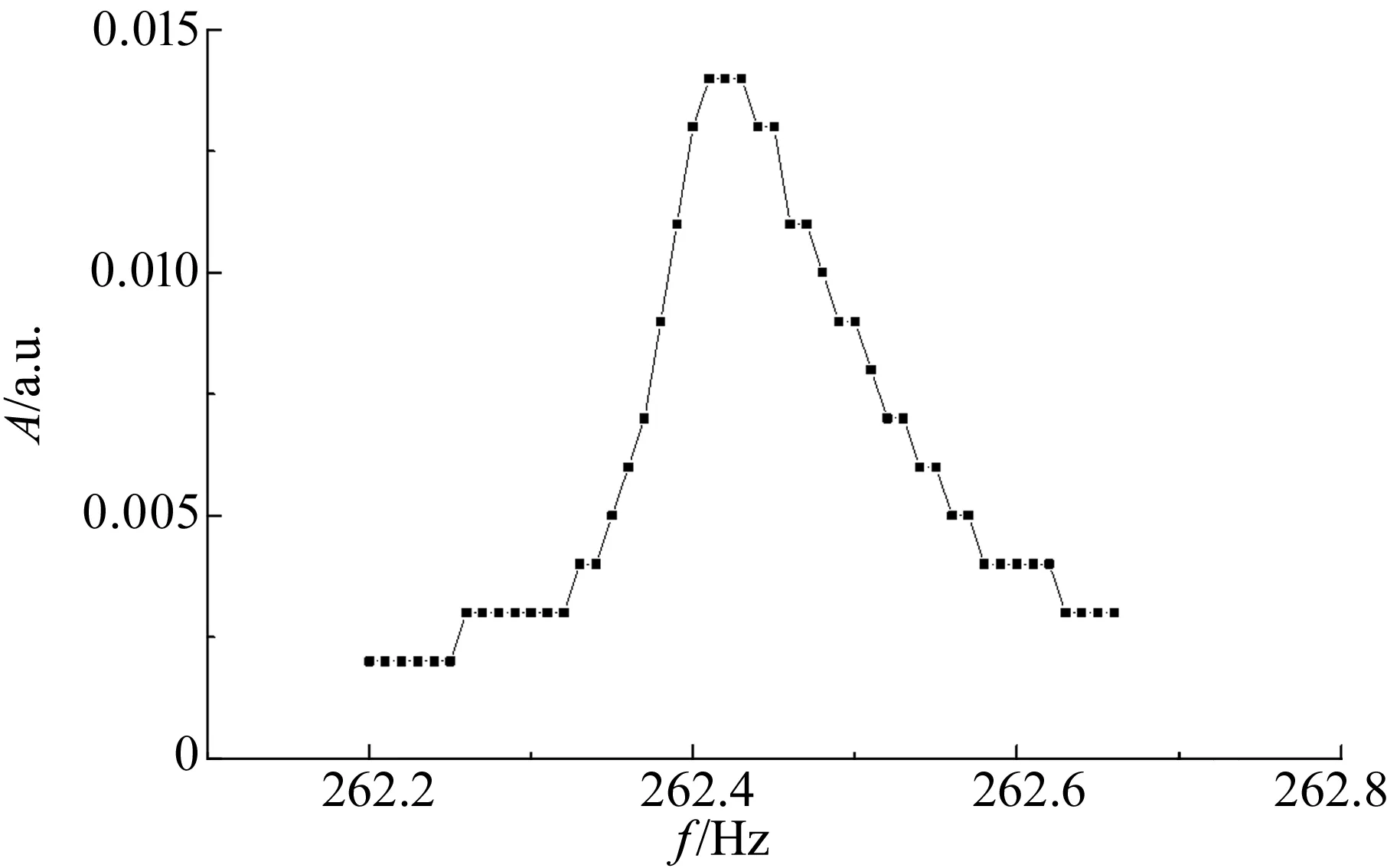
图1 麦克风法测量音叉位移振幅

1 实验原理与实验装置

本实验借助于高品质因数音叉研究受迫振动及共振现象，用带铁芯的电磁线圈产生不同频率的电磁力，作为驱动力. 搭建迈克耳孙干涉仪光路，通过激光干涉法测量位移振幅[3]. 将1面远小于音叉质量的镀银反射镜固定在音叉臂上，音叉臂端的位移会带来干涉光路光程差的改变. 从而投射到光敏传感器的干涉条纹会有吞吐，并反映到示波器上. 该实验具有不直接接触音叉、测量灵敏度高、避免电磁线圈互感等特点.

1.1高品质因子音叉

品质因数Q反映系统阻尼振动的性质，是无量纲的量.

Q<0.5时，系统为过阻尼系统，阻尼振荡时振幅随时间呈指数衰减，并不发生周期性振荡.

Q=0.5时，系统为临界阻尼系统，阻尼振荡时不发生周期性振荡.

Q>0.5时，系统为小阻尼系统，阻尼振荡时会发生周期性振荡.

记录阻尼振荡中二倍电压有效值的峰值随时间的变化关系，如图2所示，并采用指数拟合.

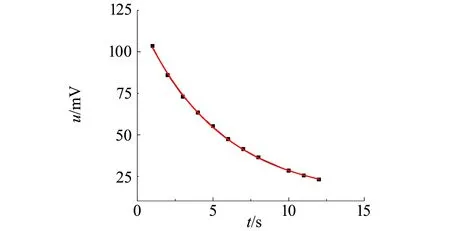
图2 阻尼振荡

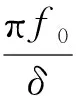
1.2电磁激励

将电磁线圈放置于铝制音叉臂的下方，并靠近音叉臂，如图3(a)所示. 对驱动线圈施加交变电流，产生交变磁场，进而产生交变的驱动力.

(a)音叉与激励线圈 (b)信号发生器 图3 音叉、激励线圈与信号发生器

交变信号通过信号发生器给出，无需使用功率放大器，信号发生器的输出同步信号用于触发示波器. 为减少镜面的偏转，减小驱动力的力矩，将激励线圈放置在靠近音叉固定端的位置.

1.3受迫振动

阻力与速度的一次方成正比的规律仅适用于速度量级为10-2m/s的极缓慢运动，一般情况下阻力与速率平方成正比的规律较符合实际情况[4]. 为了求得解析解反映振动的一般特征，假设音叉所受的阻力大小与速率成正比，若F表示阻力大小，m为振子质量，可将阻力写成

(1)

在(1)式中δ是与阻力相关的比例系数，其值取决于运动物体的形状、大小和周围介质的性质.

振子受迫振动的动力学方程为

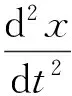
(2)

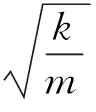
当阻尼较小时，(2)式的解为

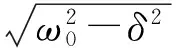
(3)

(3)式最终会趋于图4中的极限环，该极限环是椭圆形的，长轴和短轴分别为Aω和A. (3)式第一项为暂态项，经过一定时间后这一项将消失. 第二项是稳定项，在振子振动一段时间达到稳定后，其振动式即成为

x=Acos (ωt+φ) ，

(4)

达到图4中的极限环.

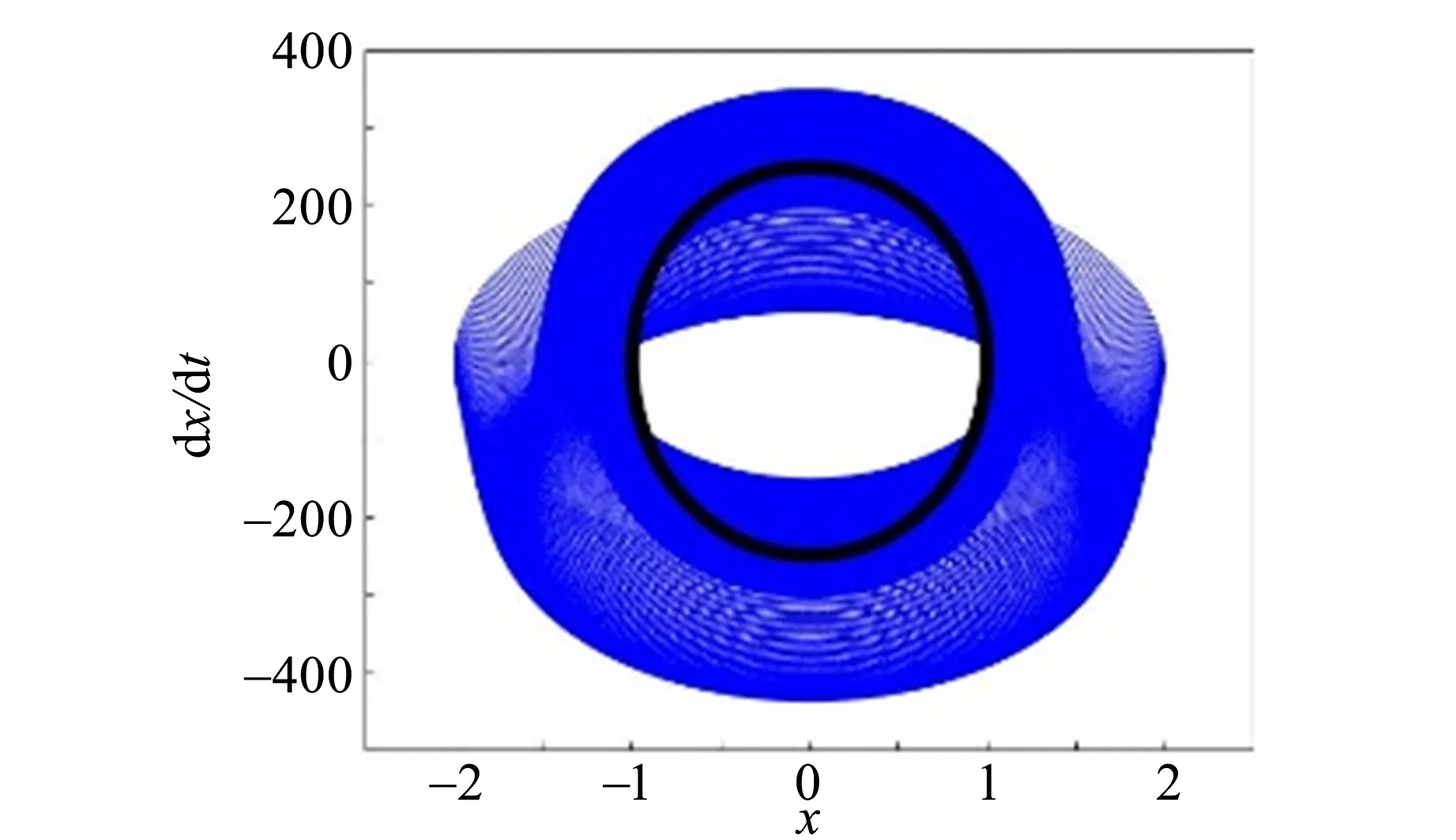
图4 受迫振动相图

1.4实验装置

干涉光路主要由λ=632.8 nm的氦氖激光器、5∶5分束镜、音叉与反射镜、反射镜、光强传感器组成，如图5所示.

(a)干涉装置

(b)镜子固定在音叉臂上图5 干涉装置

激光从激光器出发，经过分束镜，一束经过音叉上的反射镜反射，另一束经过反射镜反射，再经过分束镜，在光敏传感器中心形成干涉圆环.

随着音叉的振动，音叉上反射镜的位置发生变化，干涉光路的光程差也会发生变化.

由于光程差的变化，光敏传感器得到的干涉圆环就会有吞吐现象.

光强传感器将圆环中心的光强值转化为电压值，反映到示波器上就会得到如图6(b)的曲线，纵轴为光强传感器反馈的电压值.

(a)干涉模拟

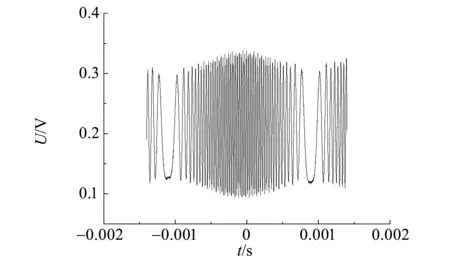
(b)波形图图6 干涉圆环及吞吐现象的波形

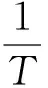
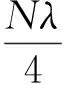
(5)

本实验中吞吐条纹个数峰值为567个，位移振幅的峰值约为0.09 mm，远远小于音叉的臂长，故可以将臂端的振动视为平动.

音叉的速度振幅为Aω，激光波长为λ，波包内周期最短部分的周期为T，则：

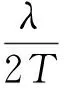
(6)

本实验中所有测量频率对应的波包内最短周期为2.81 μs，速度振幅的峰值约为0.1 m/s. 此时解析解已经不再严格，但仍能反映出该振动的一些共同特征.

2 实验方法与数据分析

可以从示波器上直接读出波包中简谐波的周期，尽量选取如图6(b)中t=0附近的波形图，在这部分的简谐波周期已经趋于稳定.

从示波器上数波包内简谐波的周期个数，进行傅里叶变换后得到常数项，并从信号中减去. 记录简谐波与x轴相交点的个数n，周期个数N为

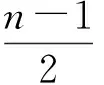
(7)

这种方法可操作性强，但实用性不高. 本实验中，位移振幅峰值附近的周期个数已经达到500个左右，计数困难，再加上环境噪声，零点附近有时会存在高频信号，这也给计数带来了困难.

本文采用一种实用性强、精度高的数据处理方法. 将实验数据离线处理，导入到Matlab，通过Wavemenu工具箱进行小波分析(图7)，小波函数选择4阶Daubechies，去除4层噪声.

输入信号为s，输出信号为a4，di为分离出来的随机噪声，则：

s=a4+d4+d3+d2+d1.

(8)

通过信号a4计算出波包内简谐波的半周期，方法也是从信号中减去傅里叶变换得到的常数项，记录简谐波与x轴相交点的个数，根据交点对应的时间值，差分后得到半周期,如图8所示.

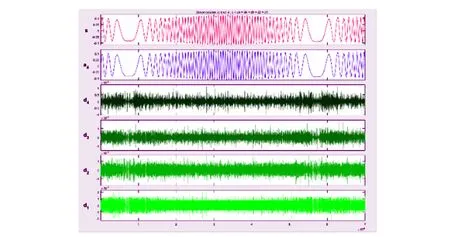
图7 Wavemenu工具箱

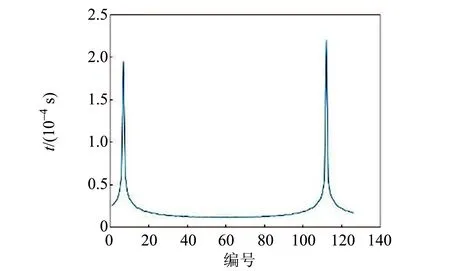
图8 波包内简谐波的半周期

从图8可以明显看出，半周期在编号40～80的范围内趋于稳定且时间最短，在此区间内求平均得到半周期.

通过周期的倒数绘制速度幅频特性曲线，纵轴为速度振幅相对值，如图9所示.

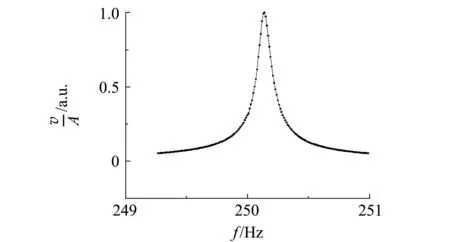
图9 速度幅频特性曲线

与此同时，通过波包内简谐波与x轴相交点的个数，也就是图8中2个峰的编号差，还可以得到位移幅频特性曲线，纵轴为位移振幅相对值，如图10所示.

音叉的位移振幅平方可以表示为

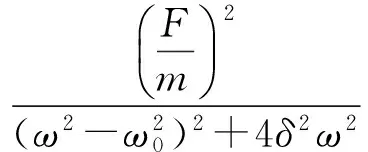
(9)

(12)式符合洛伦兹拟合的形式，拟合结果较好，但峰值下部仍存在“不对称”的现象.

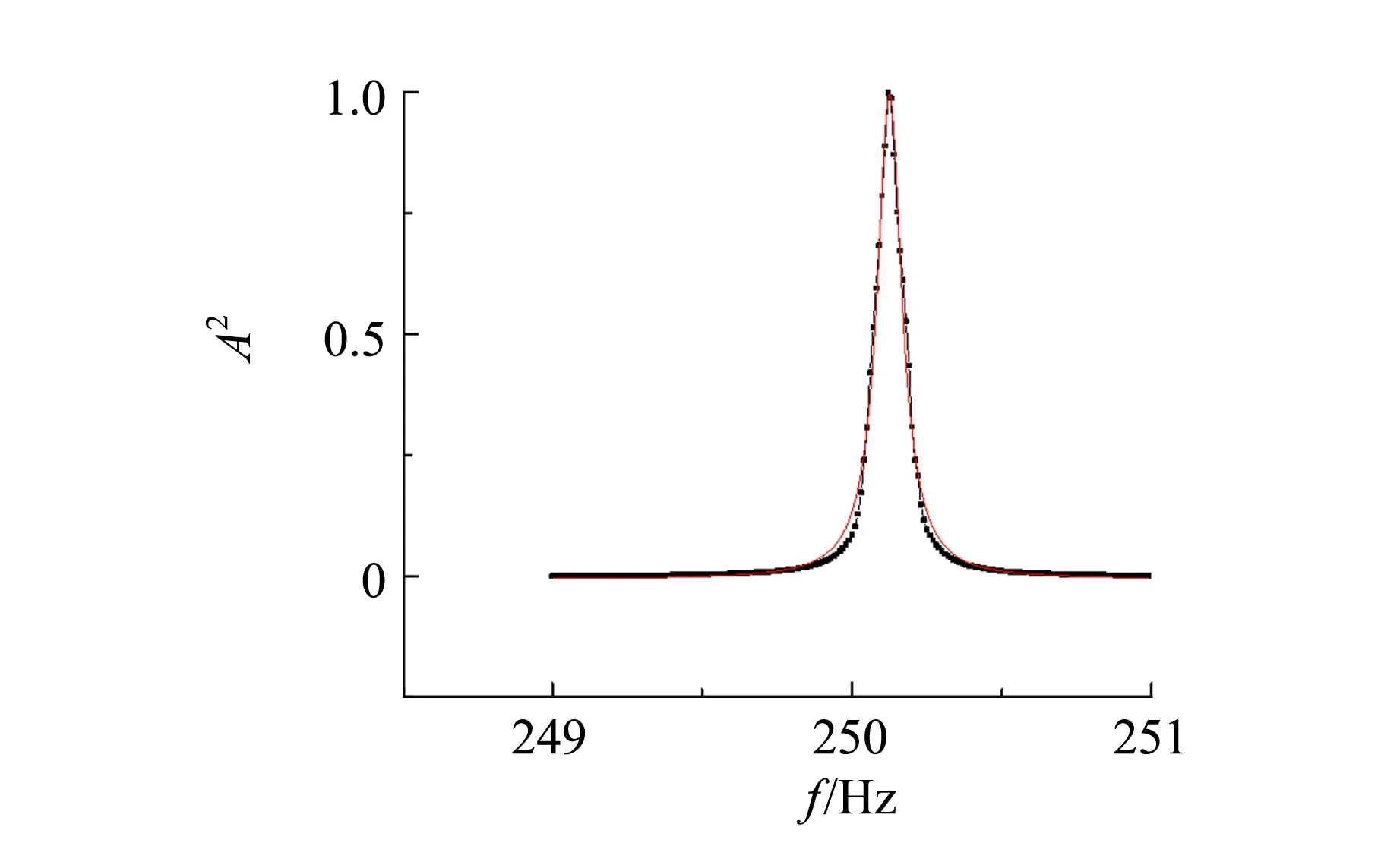
图10 位移幅频特性曲线

3 总结和讨论

通过迈克耳孙干涉装置可以同时测量速度振幅和位移振幅，位移振幅测量分度值可达μm，速度振幅通过波包内最短的简谐波周期的倒数间接测量，简谐波周期分度值可达ns. 由于测量精度高，实验中可以将音叉振动控制在μm量级.

该实验中对音叉的激励信号的电压也降到了mV量级. 电压的降低可以有效减缓伴随音叉长时间振动所带来的升温现象. 音叉的品质因子Q对温度十分敏感，如不能有效地控制温度不变，(1)式中的δ就不再是常数. 本次实验中使用的音叉品质因子较高，需要较长时间才能消除暂态过程. 通过迈克耳孙干涉装置测量音叉较微小的振动，有效地解决了这个问题.

在测量上也是直接对位移量进行测量，并可以计算出音叉臂端振动的速度值. 线圈法和麦克风法采用的都是间接测量的方式，不能真正测量到速度振幅和位移振幅. 这就带来了许多关于“速度振幅”与“位移振幅”的讨论，文献[2]中认为线圈法测量的是速度振幅，传感器法(如麦克风、压电换能片)测量的是位移振幅.

将位移幅频特性曲线和速度幅频特性曲线绘制到图11上，通过图11可以更全面地讨论“速度共振”与“位移共振”的现象. 进而分析其中的非线性因素.

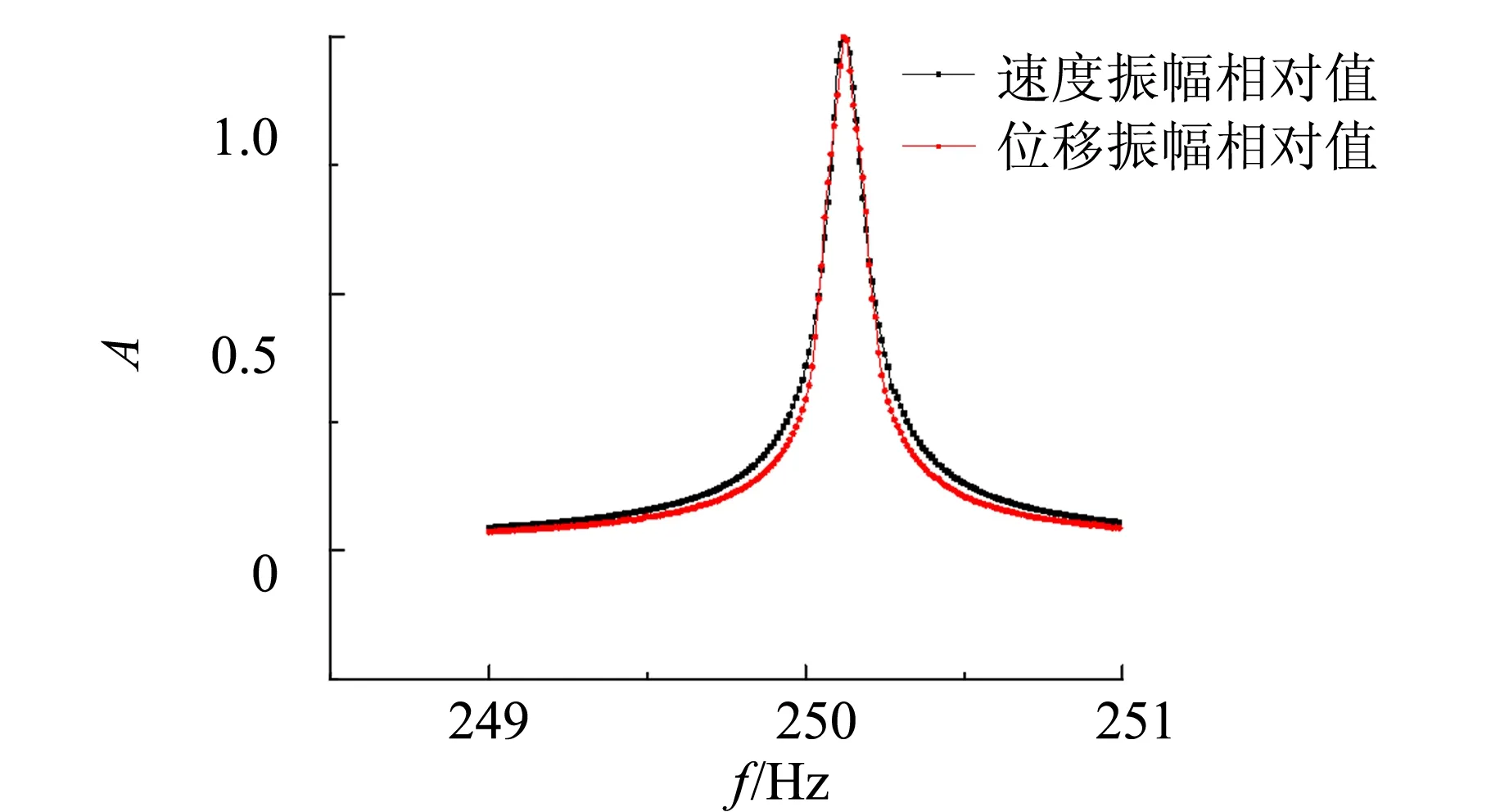
图11 速度幅频与位移幅频

[1] 张洪,曹常芳,皮厚礼. 音叉共振式液体密度测量实验的设计与实现[J]. 物理实验,2016,36(12):16-18.

[2] 倪敏,薛珍美. 音叉的速度共振与位移共振曲线的测量和研究[J]. 实验室研究与探索,2010,29(2):71-74.

[3] 徐勋义,张祖豪,刘子健,等. 基于迈克耳孙干涉的金属丝杨氏模量测量[J]. 物理实验,2016,36(9):19-22.

[4] 卢圣治. 理论力学基本教程[M]. 北京:北京师范大学出版社,2009:42.

[5] 沙振舜. 当代物理实验手册[M]. 南京:南京大学出版社,2012.

[6] 王大辉,赵学庆,张永生,等. 光学系统受迫振动的激光测量法[J]. 强激光与粒子束,2012,24(9):2017-2021.

[7] 李镇业,李培哲,周怡然,等. 大口径分光计中棱镜色散光谱线弯曲的测定[J]. 物理实验,2016,36(5):29-33.

[责任编辑：郭 伟]

Interferometryoftheforcedvibrationofatuningfork

QU Shuai, WANG Yi-rong, BAI Zai-qiao

(Department of Physics, Beijing Normal University, Beijing 100875, China)

The amplitude-frequency characteristic of the forced vibration of a tuning fork was obtained by Michelson interfering, and the displacement amplitude and velocity were measured. A high quality factor tuning fork was used in the experiment. The voltage of the excitation signal fell into millivolt level. The excitation signal, could not only eliminate the transient process, but also slow down the warming up of the tuning fork in the long incentive period. The amplitude of the tuning fork was measured using Michelson interference method, and two data processing methods were given. The advantages of this method were low driving power, high accuracy, measuring the displacement directly, and measuring two parameters at the same time.

tuning fork; high quality factor; amplitude-frequency characteristic; wavelet analysis; Michelson interference method

2017-05-02；修改日期：2017-06-11

屈 帅(1997-)，男，河南郑州人，北京师范大学物理学系励耘实验班2015级本科生.

指导教师：白在桥(1971-)，男，重庆人，北京师范大学物理学系副教授，博士，从事理论物理方面的研究工作.

O422.5

：A

：1005-4642(2017)09-0044-05