三维角联锁机织复合材料经纬向剪切性能有限元分析

，,2，，，

(1.生态纺织教育部重点实验室，江南大学纺织服装学院，江苏 无锡 214122； 2.纺织服装学院，南通大学，江苏 南通 226019)

三维角联锁机织复合材料经纬向剪切性能有限元分析

冯古雨1，曹海建1,2，王新月1，卢雪峰1，钱坤1

(1.生态纺织教育部重点实验室，江南大学纺织服装学院，江苏无锡214122；2.纺织服装学院，南通大学，江苏南通226019)

本文使用三维绘图软件Pro/E 5.0 构建出三维浅交弯联机织复合材料在经纬向模型，借助有限元软件ANSYS分别对其施加相同大小的剪切载荷作用，通过数值模拟的方法计算出复合材料及其纤维与树脂组分的剪切应力、应变分布情况。通过对其应力、应变分布情况的分析，探究三维浅交弯联机织复合材料在经纬向剪切载荷作用下的力学行为，并预测其破坏模式。结果表明：复合材料在纬向的剪切性能好于经向；纤维作为主要承载体表现出较大的剪切应力与较小的剪切应变；复合材料在剪切载荷作用下的破坏形式主要为复合材料的倾斜、坍塌及分层、纤维的脆断、树脂的破碎及纤维与树脂间的脱粘。

三维机织复合材料； 浅交弯联； 剪切性能； 有限元分析

1 引 言

三维浅交弯联机织复合材料是一种以三维浅交弯联机织物作为增强体，环氧树脂作为基体的纤维增强复合材料[1-3]。与传统的二维机织复合材料和层合板结构相比，三维浅交弯联机织物在加工过程中采用一次成型方式，弯曲的经纱将轴心不在同一个水平面上的纬纱包缠在一起，经纱的存在不仅固定了纬纱的位置，而且其在厚度方向上的分量提高了复合材料在厚度方向及层间的力学性能[4-6]。由于三维浅交弯联机织复合材料具有耐冲击、层间剪切强度高等特点，在航天航空、交通、海运、国防及工业制造等方面的应用越来越广泛[7]。

剪切载荷是复合材料在使用过程中承受的主要载荷之一，目前对于复合材料剪切性能的研究主要是应用实验及测试方法[8-10]。由于实验过程中不可避免的实验误差及对于复合材料微观力学性能表征中存在的问题，复合材料更加详细的剪切性能无法通过实验的方法得到[11]。随着计算机科学的发展，通过有限元方法模拟计算复合材料的力学行为受到越来越多研究人员的关注[12-14]。相比于实验方法，有限元模拟方法去除了实验误差的影响，更加客观地计算出了复合材料的力学性能，并且可以获得复合材料更加细致的微观力学行为[15]。

本文通过绘图软件构建出三维浅交弯联机织复合材料剪切测试模型，使用有限元分析软件ANSYS对复合材料在大小为50KN经纬向剪切载荷作用下的应力、应变分布进行模拟。通过对复合材料微观力学性能的分析，探究复合材料剪切性能在经纬向的差异；并通过对比复合材料中纤维与树脂组分的力学性能差异，探究各组分在复合材料中的相互协调作用方式；并预测复合材料的破坏形式。

2 模型建立

2.1基本假设

由于复合材料由纤维增强相与树脂基体相两部分组成，在剪切作用下两部分发挥相互协同作用，复合材料内部结构错综复杂，在构建复合材料细观结构模型时存在一定困难。为了降低建立模型时的复杂程度，并降低有限元分析时计算机的计算量，提高计算效率，在建立结构模型前作以下一些基本假设[16]：

(1)复合材料预制体中经纬纱线在相互挤压作用下，其横截面为跑道型，如图1所示，其纵向假设为连续的长丝。

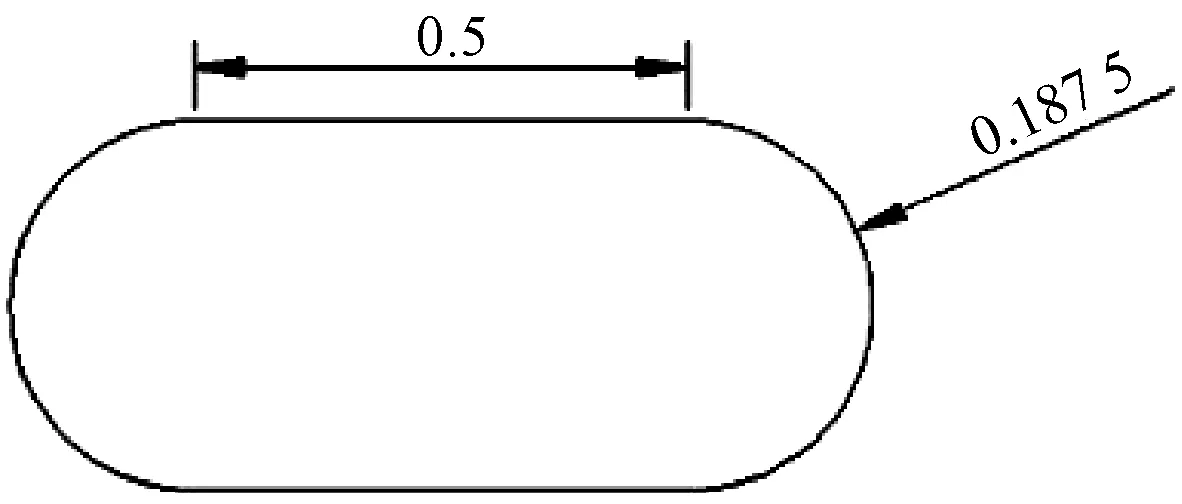
图1 经纬纱横截面示意图Fig.1 Diagram of fibers cross section

(2)预制体织造过程在一定程度上均一稳定，预制体内无疵点及不良结构的存在。

(3)复合过程中树脂基体内无气泡、裂痕等容易产生应力集中点的位置；纤维与树脂的界面性能完美，没有瑕疵的存在。

2.2模型的建立

本文使用三维绘图软件Pro/E作为工具建立复合材料细观结构模型，根据经纬纱的横截面及轨迹通过扫绘功能构建出经纬纱结构模型，通过装配功能将其装配成复合材料预制体结构模型，经纬向预制体分别如图2中(a)和(d)所示。通过切除功能构建出经纬向复合材料树脂基体结构模型，分别如图2中(b)和(e)所示。将预制体与树脂基体装配在一起形成经纬向复合材料剪切试样细观结构模型，如图2中(c)和(f)所示。

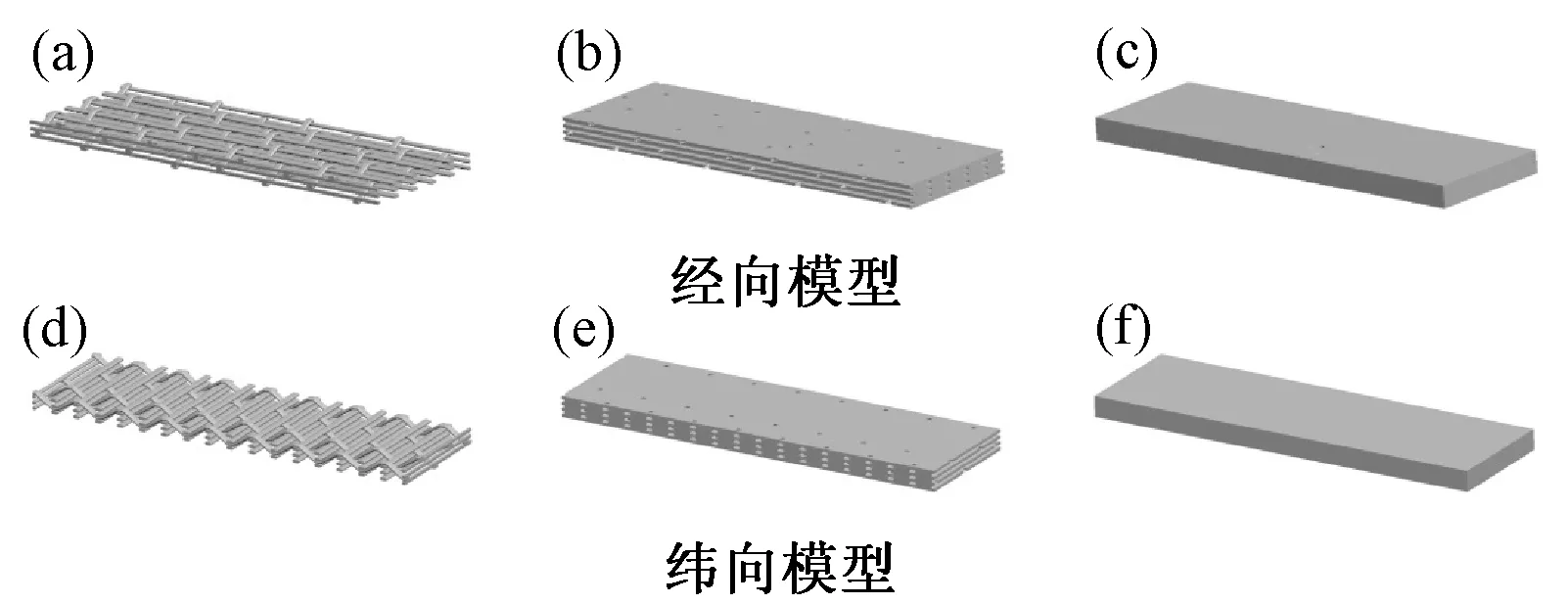
图2 复合材料经纬向细观剪切模型 (a) 经向纤维模型； (b) 经向树脂模型； (c) 经向复合材料模型； (d) 纬向纤维模型；(e) 纬向树脂模型； (f) 纬向复合材料模型Fig.2 Micro-structural model of 3D composites in warp and weft directions (a) warp fabric model; (b) warp resin model; (c) warp composites model; (d) weft fabric model; (e) weft resin model; (f) weft composites model

复合材料细观结构模型尺寸如下：预制体中经纱间距为3.33mm，纬纱间距为3mm，纬纱层间距为0.375mm。复合材料长为51mm，宽为15mm，高为2.625mm。

3 模拟计算

3.1各组分性能参数

复合材料中纤维组分定义为无捻玻璃纤维粗纱，树脂基体定义为环氧树脂E51，将两种组分的主要结构参数输入ANSYS Engineering Data中，并分别命名为E-glass Fiber和Epoxy Resin。根据之前的研究，两种组分的主要结构参数如表1所示。

表1 复合材料结构模型材料参数Table 1 Parameter of material in structure model of composites

3.2网格划分与边界条件设置

在ANSYS Geometry 中通过布尔运算将相互独立的经纬纱粘接在一起作为一个受力整体进行分析。

本文使用较为常用的ANSYS Meshing方法对复合材料结构模型进行网格划分，ANSYS Meshing按网格划分手段可分为自动划分法、扫描法、多区域法；按网格类型提供了四面体法、六面体法及两种方法的结合方法。本文使用尺寸为0.5mm的六面体法的自动划分法对复合材料进行网格划分。相同计算精度下六面体法使用更少的网格，减少了计算量；虽然网格局部加密会使计算结果更加精确，但本文使用的复合材料模型结构较为均匀，不易出现明显的应力集中点，自动划分法已经可以满足计算精度的要求。

经过网格划分后的复合材料经纬向剪切模型如图3所示，其中经向剪切模型中纤维由102223个节点和46258个网格单元组成，树脂由179944个节点和106436个网格单元组成。纬向剪切模型中纤维由64212个节点和29277个网格单元组成，树脂由118760个节点和70837个网格单元组成。

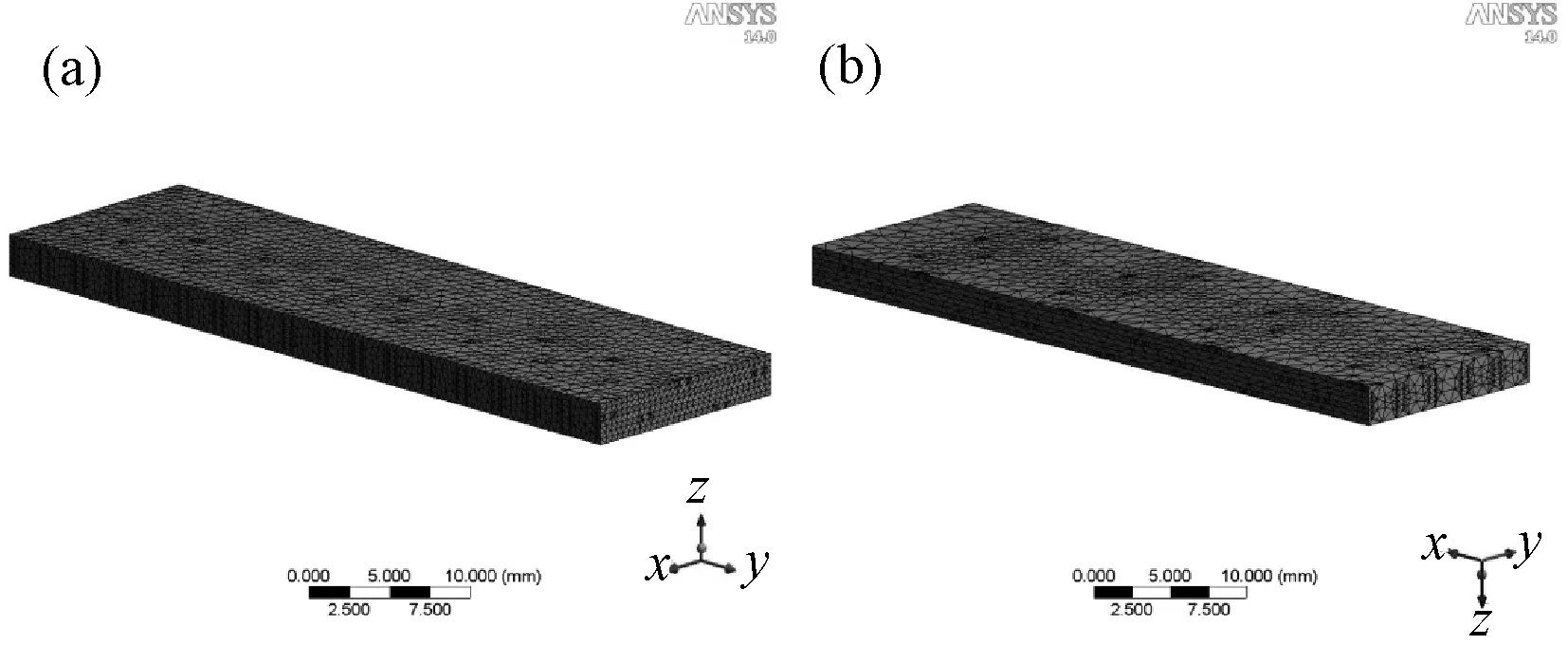
图3 划分网格后的经纬向复合材料结构模型 (a) 经向； (b) 纬向Fig.3 Structural model of 3D composites in warp and weft directions after meshing (a) warp; (b) weft

在复合材料模型上设置普通循环边界条件，对复合材料的底面施加Fixed Support 完全固定边界条件，四个侧面设定为Free条件，在顶面施加经纬向复合材料试样相应方向50kN的载荷。

4 结果与分析

4.1复合材料剪切力学性能

复合材料经纬向剪切应力、应变分布情况如图4所示。

由图4可以看出，复合材料在经纬向剪切载荷的作用下上表面发生倾倒、错位，且表面出现垂直于载荷方向的褶皱。上表面左侧在剪切载荷作用下翘起，右侧下陷。经向复合材料最大剪切应力为1121.9MPa，最大剪切应变为0.16221；纬向复合材料最大剪切应力为647.88MPa，最大剪切应变为0.10888。

通过以上数据分析可知，在50kN剪切载荷作用下，经向复合材料剪切试样相比于纬向复合材料剪切试样表现出更大的最大剪切应力和最大剪切应变，这说明复合材料在经向剪切载荷作用下更容易发生破坏，且会发生更大的变形。复合材料表现出明显的剪切各向异性。为了更好地分析复合材料中纤维与树脂协同作用机理，将两种组分分开，分别考察纤维与树脂中剪切应力、应变的分布。

4.2复合材料各组分剪切力学性能

经向复合材料剪切试样中纤维与树脂组分的应力、应变分布情况如图5所示；纬向复合材料剪切试样中纤维与树脂组分应力、应变分布情况如图6所示。

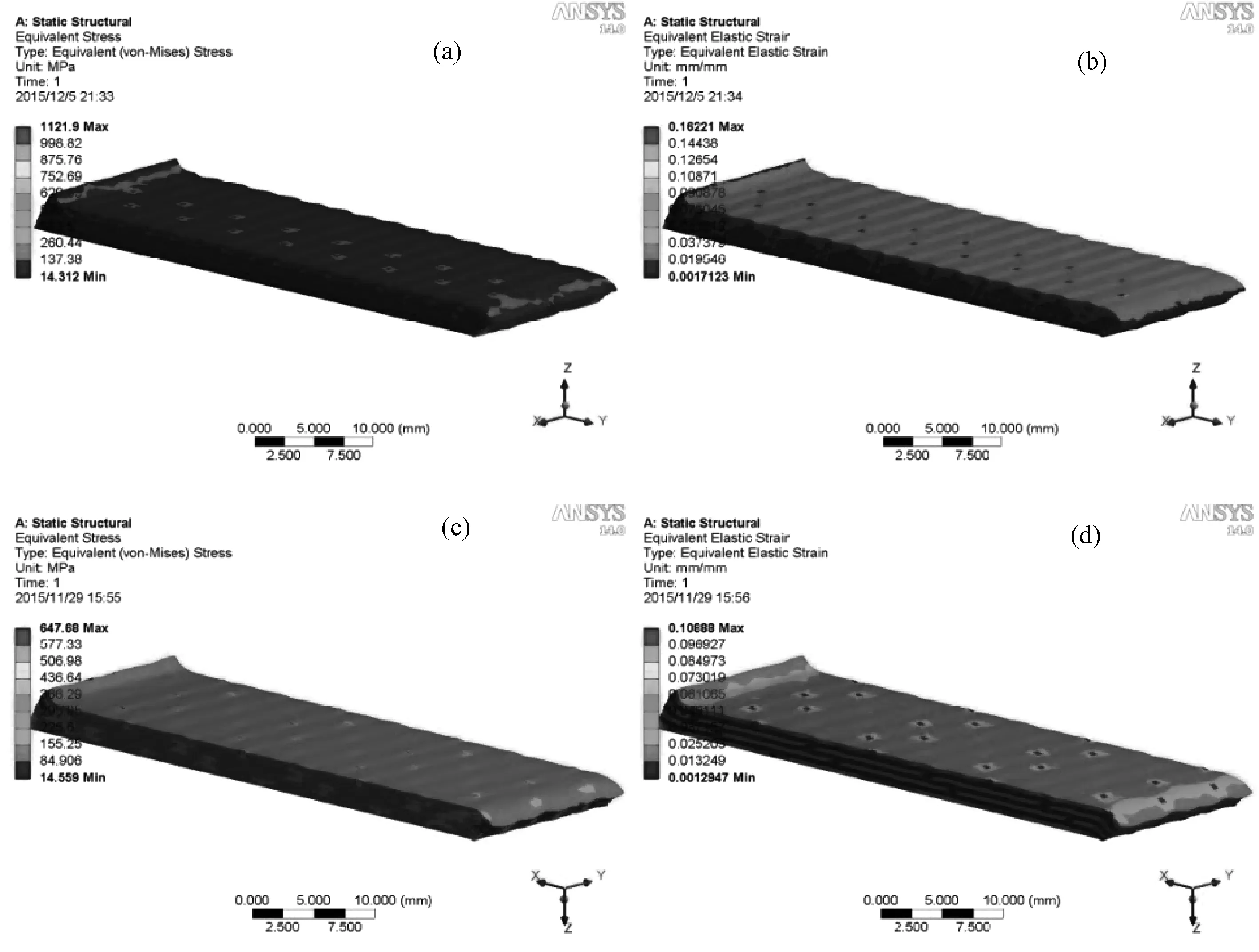
图4 经纬向复合材料剪切应力、应变分布图 (a) 经向剪切应力； (b) 经向剪切应变； (c) 纬向剪切应力； (d) 纬向剪切应变Fig.4 Distribution of shear stress and shear strain of 3D composite in warp and weft direction (a) shear stress on warp; (b) shear strain on warp; (c) shear stress on weft; (d) shear strain on weft

由图5(a)、(b)分析可知，经向复合材料预制体中经纱相比于纬纱表现出更大的剪切应力与剪切应变，。这是由于纬向预制体中轴向与载荷方向平行的纬纱同样承受较大的载荷作用，轴向垂直于载荷方向的经纱主要起连接纬纱与传递载荷的作用；密度较大的纬纱降低了剪切载荷在每根纬纱上的平均作用，而密度较小的经纱在承担起连接纬纱与传递载荷的作用时，平均作用在每根经纱上的载荷作用增加，在这一增一减的作用下，纬向复合材料预制体中经纬纱剪切应力、应变较为平均，复合材料的整体性增强。

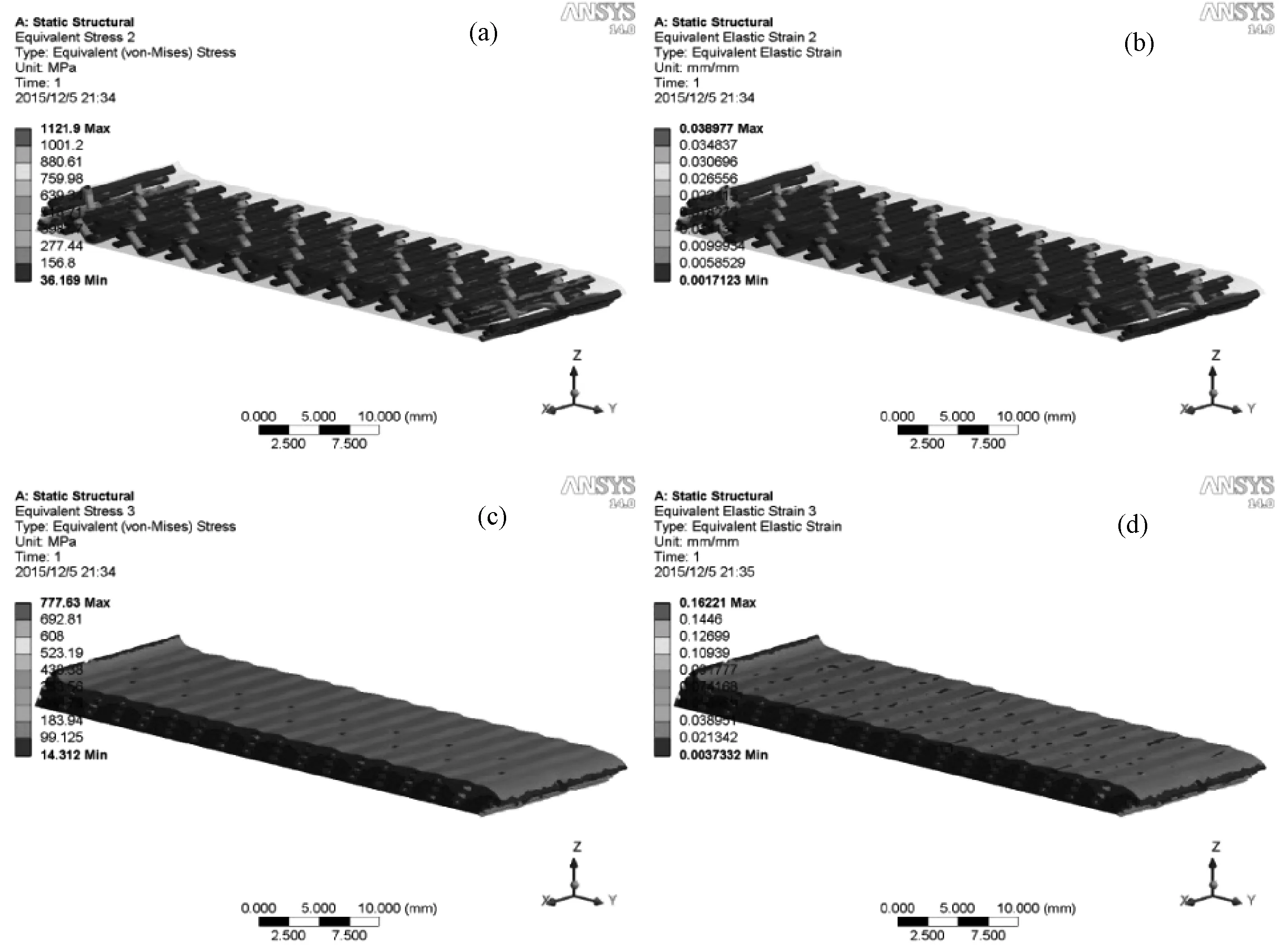
图5 经向复合材料各组分剪切应力、应变分布 (a) 经向纤维剪切应力； (b) 经向纤维剪切应变； (c) 经向树脂剪切应力； (c) 经向树脂剪切应变Fig.5 Distribution of shear stress and shear strain of fibers and resin in warp direction (a) shear stress of fabric on warp; (b) shear strain of fabric on warp; (c) shear stress of resin on warp; (d) shear strain of resin on warp

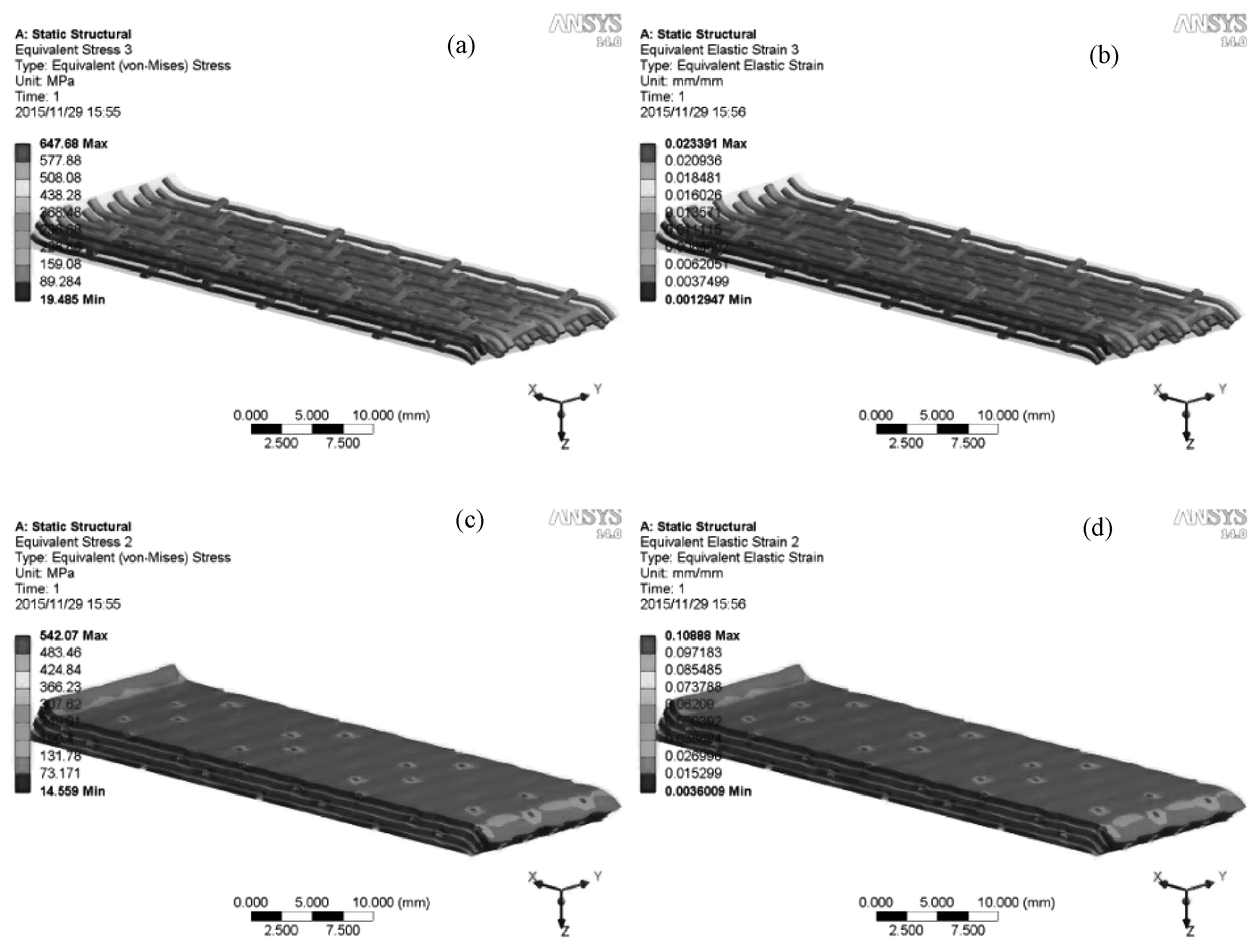
图6 纬向复合材料各组分剪切应力、应变分布 (a) 纬向纤维剪切应力； (b) 纬向纤维剪切应变； (c) 纬向树脂剪切应力； (c) 纬向树脂剪切应变Fig.6 Distribution of shear stress and shear strain of fibers and resin in weft direction (a) shear stress of fabric on weft; (b) shear strain of fabric on weft; (c) shear stress of resin on weft; (d) shear strain of resin on weft

这说明在经向剪切作用下，经纱更容易发生破坏。这是由于相对于轴向垂直于载荷方向的纬纱，轴向平行于剪切载荷方向的经纱承受更大的载荷作用，而纬纱主要起到的是连接经纱及传递载荷的作用；经密与纬密的差别也是出现这种现象的原因之一，相比于数量密度较大的纬纱，经纱在载荷作用下更容易发生破坏。对比图6(a)、(b)可以看出，纬向复合材料预制体中经纬纱剪切应力、应变差别并不明显，载荷作用分布较为均匀[17]

对比经纬向复合材料中纤维组分与树脂组分可以看出，无论在经向或是纬向剪切载荷作用下，相比于树脂组分，复合材料中纤维组分均表现出更大的剪切应力与更小的剪切应变。这是由于纤维具有较大的杨氏模量预拉伸强度，在复合材料中作为主要承载体承受更多的载荷作用；而树脂基体具有较小的杨氏模量与较大的泊松比，在载荷作用下更容易发生变形。

结合图5、图6分析，复合材料在剪切载荷作用下轴向平行于载荷方向的纤维产生较大的应力和应变，当其应力或应变达到其破坏准则时，纤维发生脆断破坏；轴向平行于载荷方向的纤维发生程度不同的偏移，这种变形程度的差异也是复合材料表面出现垂直于载荷方向褶皱的原因；随着变形程度的增加，复合材料会出现层间坍塌、分层等现象。当树脂基体的应力、应变值超过其破坏准则时，树脂基体会出现破碎、脱落等现象。对比图5(b)、(d)与图6(b)、(d)，复合材料中两种组分的应变存在明显差异，这种差异意味着在剪切作用下纤维与树脂的变形程度不同，在纤维与树脂的界面上分布的载荷对复合材料的界面性能产生一定的破坏，纤维与树脂间出现脱粘现象，纤维从树脂中拔出。

5 结 论

1.相较于纬向，三维浅交弯联机织复合材料在经向剪切载荷作用下表现出更大的剪切应力与剪切应变，其纬向剪切性能优于经向。

2.复合材料中纤维作为主要承载体承受更大的剪切应力，树脂基体作为次要承载体呈现较大的剪切应变。

3.三维浅交弯联机织复合材料在剪切载荷作用下出现沿剪切载荷方向的倾倒、坍塌现象，表面出现垂直于载荷方向的褶皱；破坏模式主要为复合材料的分层、纤维的脆断、树脂的破碎及纤维与树脂间的脱粘。

[1] Cox B N, Dadkhah M S, Morris W L. On the Tensile Failure of 3D Woven Composites[J]. Composites Part A: Applied Science and Manufacturing, 1996, 27(6): 447～458.

[2] Mouritz A P. Tensile Fatigue Properties of 3D Composites with Through-thickness Reinforcement[J]. Composites Science and Technology, 2008, 68(12): 2503～2510.

[3] Veedu V P, Cao A, Li X, et al. Multifunctional Composites using Reinforced Laminae with Carbon-nanotube Forests[J]. Nature Materials, 2006, 5(6): 457～462.

[4] 冯古雨,曹海建,钱坤. 树脂含量对装甲车体内饰用轻质复合材料弯曲性能的影响[J]. 宇航材料工艺, 2015, 5:26～30.

[5] 卢雪峰，冯古雨，等.三维浅交弯联机织复合材料拉伸性能的有限元分析[J].材料科学与工程学报， 2016， 34(6)：988.

[6] Ausiello P, Apicella A, Davidson C L. Effect of Adhesive Layer Properties on Stress Distribution in Composite Restorations—a 3D Finite element analysis[J]. Dental Materials, 2002, 18(4): 295～303.

[7] Mahesh S, Phoenix S L, Beyerlein I J. Strength Distributions and Size Effects for 2D and 3D Composites with Weibull Fibers in an Elastic Matrix[J]. International Journal of Fracture, 2002, 115(1): 41～85.

[8] Brandt J, Drechsler K, Arendts F J. Mechanical Performance of Composites Based on Various Three-dimensional Woven-fibre Preforms[J]. Composites Science and Technology, 1996, 56(3): 381～386.

[9] 蔡永明，孙慧玉.树脂基三维编织复合材料粘弹性能的数值预报[J]. 材料科学与工程学报， 2012， 30(2)： 271.

[10] Hallal A, Younes R, Nehme S, et al. A Corrective Function for the Estimation of the Longitudinal Young’s Modulus in a Developed Analytical Model for 2.5 D Woven Composites[J]. Journal of Composite Materials, 2011, 45(17): 1793～1804.

[11] Hallai A, Younes R, Nehme Setal. A corrective Function for the Estimation of the Longitudinal Yong’s Modulus in a Developed Analytical Model for 2.5D Woven Composites[J].Journal of Composite Materials, 2011, 45(17):1793.

[12] Lomov S V, Gusakov A V, Huysmans G, et al. Textile Geometry Preprocessor for Meso-mechanical Models of Woven Composites[J]. Composites Science and Technology, 2000, 60(11): 2083～2095.

[13] Zeng T, Wu L, Guo L. Mechanical Analysis of 3D Braided Composites: a Finite Element Model[J]. Composite Structures, 2004, 64(3): 399～404.

[14] Zako M, Uetsuji Y, Kurashiki T. Finite Element Analysis of Damaged Woven Fabric Composite Materials[J]. Composites Science and Technology, 2003, 63(3): 507～516.

[15] Verpoest I, Lomov S V. Virtual Textile Composites Software WiseTex: Integration with Micro-mechanical, Permeability and Structural Analysis[J]. Composites Science and Technology, 2005, 65(15): 2563～2574.

[16] Ha-Minh C, Boussu F, Kanit T, et al. Analysis on Failure Mechanisms of an interlock Woven Fabric under Ballistic Impact[J]. Engineering Failure Analysis, 2011, 18(8): 2179～2187.

[17] 董纪伟，冯淼林，等.基于均匀化理论的三维编织复合材料弯曲细观应力数值模拟[J].材料科学与工程学报， 2010， 28(6)：801～805+822.

FiniteElementAnalysisonShearPropertyinWarpandWeftDirectionof3DAngleInterlockComposites

FENGGuyu1,CAOHaijian1,2,WANGXinyue1,LUXuefeng1,QIANKun1

(1.KeyLaboratoryofEco-TextileofMinistryofEducation,Jiangnanuniversity,Wuxi214122，China;2.Collegeoftextileandclothing,Nantonguniversity,Nantong226019,China)

3D curved-shallow crossing-linking composite models in warp and weft directions were established by mapping software Pro/E 5.0. The shear stress and strain distribution of the composite models were investigated with the help of finite element software ANSYS. The mechanical behavior and failure mode of the 3D composite were studied and predicted by analyzing the shear stress and strain distribution under shear load in warp and weft directions. The results showed that 3D composite had better shear property in weft direction than in warp direction. Compared to resin matrix, fiber made the major contribution to subject the shear load, showing larger shear stress and smaller shear strain. Incline, collapse, and delamination occurred in the 3D composite subjected to shear load. In addition, brittle failure of fibers, fracture of resin matrix, and debond between fiber and resin matrix occurred in the 3D composite subjected to shear load at the same time.

3D woven composite; curved shallow crossing linking; shear property; finite element analysis

TB332

：ADOI:10.14136/j.cnki.issn1673-2812.2017.04.026

1673-2812(2017)04-0650-05

2015-12-28；

：2016-05-26

“十三五”国家重点研发计划资助项目(2016YFB0303205)，江苏省自然科学基金-青年基金资助项目(BK20160157)，江苏省产学研前瞻性联合研究资助项目(BY2015019-33、BY2016022-07)，中央高校基本科研业务费专项资金资助项目(JUSRP51505)，江苏高校优势学科建设工程资助项目

冯古雨(1992-)，男，硕士研究生。主要从事纺织复合材料的制备及性能研究。E-mail：fengguyu890@163.com。

钱 坤(1963-)，男，教授，博士生导师。主要从事轻量化复合材料的制备及应用。E-mail：qiankun_8@163.com。