厚砂土层斜井井壁应力分布规律三维光弹性模型试验

周檀君，周国庆，廖 波,2，张海洋,赖泽金，陶祥令,3

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008; 2.浙江工商大学 技术与工程管理系，浙江 杭州 310018;3.江苏建筑职业技术学校 能源与交通工程学院，江苏 徐州 221116)

厚砂土层斜井井壁应力分布规律三维光弹性模型试验

周檀君1，周国庆1，廖 波1,2，张海洋1,赖泽金1，陶祥令1,3

(1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221008; 2.浙江工商大学 技术与工程管理系，浙江 杭州 310018;3.江苏建筑职业技术学校 能源与交通工程学院，江苏 徐州 221116)

以穿越厚砂土层的某煤矿主斜井为工程背景，设计了物理模型试验，建立了斜井井壁三维光弹性应力冻结试验方法。实现了考虑斜向倾角作用下穿越厚砂土层斜井井壁应力状态的三维试验模拟，并结合应力冻结后模型横、纵向切片光弹测试得到的全场最大剪应力等值线图对井壁应力随埋深、环向角度变化规律进行了分析。研究结果表明，井壁横向切片内应力水平和应力分布不均匀性均远大于纵向切片，最大剪应力的应力集中区域出现在井壁两帮内缘水平面±25°范围内，斜井井壁顶部最大剪应力大于底部;随斜井井壁埋深增加，纵向应力近似线性增加，但不同环向角度对应的应力增加速度差异较大，从而导致不同埋深位置，井壁内部应力的量值和分布规律均有差异。

斜井井壁;模型试验;应力分布规律;光弹性应力冻结法

近年来，随着我国内蒙古、宁夏、新疆等西部地区煤田的开发，煤矿新井建设重心逐渐由东部向西部转移，这些地区地质构造相对简单，煤层较厚埋深较浅，煤炭储量丰富，建设大型煤矿尤其适合采用斜井或者斜井-立井联合开拓方式[1]进行煤炭开采。

与立井井壁设计理论的大量研究成果[2-7]相比，针对斜井井壁设计理论的研究较少。 《煤矿斜井井筒及硐室设计规范》(GB 50415—2007)只给出了支护方式的选择原则，并未涉及井壁设计方法[8]。《采矿工程设计手册(中册)》中指出，当倾角大于80°时，按立井计算地压，当倾角小于60°时按平硐计算地压;按平巷计算侧压力，支护类型与厚度按巷道计算[9]。由于斜轴向的影响，斜井井壁受有径向荷载、环向和轴向剪切荷载等3类荷载，3类荷载随井筒倾角变化，所受荷载远比立井与巷道复杂[10]。按传统方法设计的斜井井筒破坏事故时有发生。如宝鸡秦源矿主斜井倾角17.5°，在表土层78 m处，现浇混凝土及料石砌碹段井壁发生断裂、顶底板及两帮强烈相对移近，井壁维护困难[11];大佛寺矿主斜井在斜长100～400 m的范围内有19处发生较大的井壁淋水，涌水量达30 m3/h[12]。因此，为探究表土段斜井井壁破坏机理，有必要对斜井井壁应力分布规律进行研究，为建立科学合理的斜井井壁设计理论与计算方法奠定基础，为现场的支护设计和施工提供参考。

目前，有些学者通过采用平面应变或平面应力模型试验方法，研究和探讨了斜井井壁及围岩稳定性问题，取得了一定进展，如闫振东等[13]通过模型试验，对渐进加载作用下渗流状态时厚砾石层斜井围岩破坏过程及破坏过程中围岩压力和围岩位移变化规律进行了研究。岳中文等[14]对加载作用下富水斜井围岩破坏过程中围岩压力、位移和孔隙水压力变化规律进了研究。王卫军等[15]对采动条件下底板应力的分布和传播规律及其与巷道围岩应力的关系、底板暗斜井受回采过程扰动的动态变形破坏特征、底板巷道的失稳机制及控制方法进行了系统研究。

从力学层面上来说，斜井井壁受力状态并非简单的平面应变或平面应力问题，斜井倾角会对井壁应力分布规律产生影响[16]。笔者以穿越厚砂土层的某煤矿主斜井为原型，采用三维光弹性应力冻结模型试验方法，对斜井井壁应力分布规律进行模拟研究。

1 光弹性应力冻结模型试验原理

光弹性法是基于应力-光学定律的一种较为成熟的应力测试方法，能够直观地反映出结构在荷载作用下弹性阶段内的全场应力分布规律[17]。光弹性应力冻结试验原理是在常规光弹性试验基础上，引入有机化合物多相理论，利用光弹模型处于临界温度时能保存应变及双折射效应这一特性，采用先冻结后切片观测的方法，实现对处于复杂环境中的模型内部应力规律进行观测。

由上可知，该试验方法应用于岩土工程地下结构模型试验是尤为合适的。本文采用了该试验方法，利用自主设计的地下结构相互作用光弹性应力冻结试验系统，针对斜井井壁受力特性设计了三维光弹性应力冻结模型试验，对斜井井壁应力分布规律进行了研究。

2 试验方案

光弹性试验过程处于弹性阶段，根据弹性力学叠加原理，模型本身具有自相似性，在确保边界荷载分布特征形式相似的原则下，边界荷载值与内部应力值存在对应比例关系不随荷载数值变化，即可人为设定相同荷载分布特征的边界荷载值，进行试验得到模型内部应力，再通过模型自相似缩比及模化相似缩比换算得到对应原型内部应力值。需要注意的是砂土介质为非理想弹性材料，故应力换算结果对实际工程也只是一种近似反映。

为了研究厚砂土层斜井井壁应力分布规律，试验拟对以15°倾角穿越砂质地层斜长200～280 m段井筒进行模型，上覆地层平均容重γ=19 kN/m3，原型井筒对应垂直埋深、地压分别为51.8～72.5 m,0.98～1.38 MPa。

考虑到光弹仪尺寸，选定几何相似常数Cl=100，为了便于模型制作加工，采用厚壁筒结构近似模拟斜井井筒，模型内外径分别取40,66 mm，根据几何缩比模型长度取800 mm。应力冻结温度120 ℃下的环氧模型弹模为25 MPa，C30井壁混凝土弹性模量为3 GPa，根据相似理论，确定应力、弹模相似常数:Cσ=Cc=1 200。

通常为了获得较为明显的试验结果，以模型内部出现5～8级等差条纹为宜，根据类似地下斜埋筒形结构理论解[16]及应力-光学定律[18]，计算得到对应模型垂直荷载为0.072 5～0.010 2 MPa，可得应力换算常数为13.52。

试验砂土选用福建标准砂，平均粒径d50=0.17 mm，土粒比重为2.633。为确保模型地层均匀性，采用砂雨法[19]和分层夯实法制备砂质模型地层，最终获得干砂地层相对密实度为65%。地层土参数见表1。

表1模型试验福建标准砂基本参数
Table1ParametersofFujiansandtests

内摩擦角/(°)黏聚力/kPa相对密实度/%干密度/(g·cm-3)饱和密度/(g·cm-3)247065152195

3 模型制作与试验设计

3.1 模型制作

针对斜井井壁力学特性以及三维应力冻结光弹性试验的需要，选择黏度低、流动性好、透明度好的618号环氧树脂作为模型材料。以顺丁烯二酸酐作为固化剂，可使环氧树脂由流动性的线性高聚物变成立体网状结构的热固性固体。为了缩短固化周期和提高稳定性，加入催化剂—二甲基苯胺。3种原料按质量配比为:618号环氧树脂∶固化剂∶催化剂=100∶35∶0.05。

模型制作工艺如下：

(1)根据模型材料的配比及模型容积计算出每种材料的需要量，将称取所需量的618号环氧树脂倒入不锈钢或搪瓷容器中，放入电热箱中加热至120 ℃，恒温2～3 h，让挥发物散出，然后自然降温至60～65 ℃，在电热箱中恒温。

(2)称取所需量的固化剂顺丁烯二酸酐，将瓶装顺丁烯二酸酐瓶盖松开，水浴加热至60～65 ℃，待全部熔化后倒入玻璃容器中，然后用平板玻璃盖上开口端，放入60 ℃电热箱中恒温。

(3)将熔化后恒温的顺丁烯二酸酐及催化剂二甲基苯胺缓缓倒入55～60 ℃的环氧树脂中，利用搅拌机慢速搅拌，使混合料恒温在55～60 ℃，搅拌1.5～2 h，搅拌过程在油浴中恒温。搅拌完毕后，将混合液放入真空干燥箱抽真空10～20 min以排除气泡。

(4)采用离心法将熔化后的58号石蜡均匀涂抹在模具表面作为脱模剂，将45～50 ℃混合液按底浇筑法缓缓注入经过预热的模具中。为了保证模型应力冻结性能，采用二次固化工艺，完成第1阶段40 ℃环境7 d固化后，从模具中取出初凝的模型，放入硅油中进行后续二阶段油浴固化。固化过程温度控制曲线如图1所示。

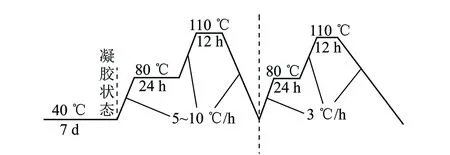
图1 固化过程控温曲线Fig.1 Temperature control curves of curing process

固化后模型与原型参数见表2。

表2模型井壁与原型井壁参数
Table2Shaftwallparametersofmodelandprototype

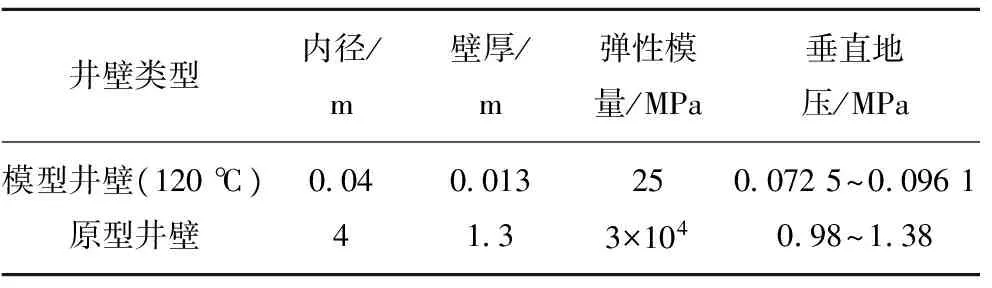
井壁类型内径/m壁厚/m弹性模量/MPa垂直地压/MPa模型井壁(120℃)00400132500725～00961原型井壁4133×104098～138

(5)待模型胚料完成全阶段固化后，通过机加工获得形状和尺寸精确符合试验要求的模型如图2所示。

图2 斜井井壁光弹模型
Fig.2 Photoelastic model of inclined shaft

3.2 试验装置

利用深部岩土力学与地下工程国家重点实验室自主设计、研制的地下结构相互作用光弹性应力冻结试验系统完成试验，试验系统如图3所示。

图3 应力冻结试验系统Fig.3 Tests system of stress freezing

系统由模型箱、温度控制室、框架式自平衡反力架、测试采集系统、分布式杠杆加载系统组成。

试验系统主要技术指标：

(1)模型试验箱内尺寸：1 000 mm×1 400 mm×1 000 mm。

(2)温度控制室控温范围20～300 ℃，控温精度0.5 ℃。

(3)模型上边界的12块平行加载板通过连接相互独立的杠杆加载系统，可以施加阶梯形荷载，阶梯荷载集度范围0～0.2 MPa，最小宽度为120 mm，该加载系统可以近似模拟随斜井井筒埋深增加而递增的上覆地层压力。

(4)测试数据采集系统，压力传感器采用自研自制压阻式分布压力传感器和TD-LY350微型土压力盒，温度测试采用PT100铂热电阻，数据采集仪采用datetaker DT85智能数据采集仪，如图4所示。

3.3 试验布置与加载方式

(1)模型箱布置

模型试验的边界效应主要来自模型箱边壁对模型的约束作用，当模型中结构物与模型箱侧壁相对较近时，模型箱边界的约束会明显影响模型本身的性状[19]。本试验模型斜井埋深为0.27 m，模型井筒外径0.066 m，模型箱侧壁与模型最小距离大于4.7D(D为模型井筒外径)，斜井模型最深位置与模型箱底距离大于11D，可忽略边界效应。

(2)测点布置

通过利用光弹仪对应力冻结后的模型切片观测得到等差、等倾线条纹，对其进行分析能获得模型内部应力规律，为了获得更多模型边界应力值，本试验采用微型土压力盒和分布式压力传感器对斜井井壁模型3个断面的外侧土压力进行测试，同时在模型井筒周边布置了T1～T5温度传感器，便于在应力冻结过程当中，对模型井筒温度进行检测，确保应力冻结有效性。分布式压力传感器安装如图5所示，微型土压力P1～P12和温度传感器T1～T5布置位置如图6所示。

图4 测试采集系统Fig.4 Testing and acquisition system

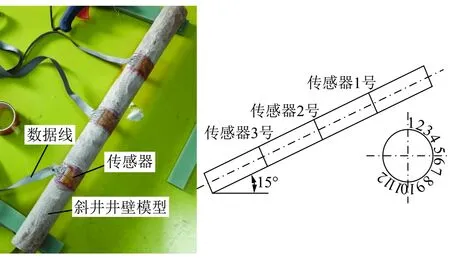
图5 分布式压力传感器布置Fig.5 Layout of distributed pressure sensor

(3)试验加载布置

由于斜井轴向倾角的存在，随斜井深度增加井壁上覆地层压力亦逐渐增大，本试验通过在上边界施加沿模型深度方向逐级增加的阶梯荷载，模拟随斜井深度逐渐增加的井壁上覆地层压力，为了保证应力冻结过程中荷载施加的准确性采用杠杆加载法，加载过程采用每级增载数值为总荷载1/3的逐级增载法，每级荷载从较小荷载端往较大荷载端依次施加，各杠杆所施加的最终荷载见表3。待荷载完成施加后，预压固结12 h，再进行应力冻结试验。

表3杠杆加载系统阶梯荷载
Table3Steploadvalueofleverloadingsystem

加载板编号L1L2L3L4L5L6L7L8L9L10L11L12模型荷载/kPa641683725767809851894936978102010621104原型荷载/MPa086092098104109115121127132138144149原型地层深度/m46149452756593626659692725758791824

3.4 模型应力的冻结和切片

光弹性材料应力冻结原理是基于有机化合物的多相理论[21]。温度逐渐升高时，有机化合物内部各种塑性相及粘弹性相逐渐软化，到达临界软化温度时，它们被完全“解体”，而弹性相的软化温度比前者高得多，因此这时弹性依然存在，所以材料呈完全弹性(或高弹性)特性，这个特定温度称为应力冻结的临界温度。对于本试验所采用的模型材料，临界温度为120 ℃。在临界温度以上对模型加载，荷载由弹性相物质独自承受;而当温度逐渐降低时，塑性相及粘弹性相物质又逐渐恢复变硬，将弹性相已经产生的变形固定下来;当温度回到常温再把荷载卸除时，多相物质之间的相互约束使他们不能恢复最初不受载时的形态，而基本上把高温时的应变及双折射效应保留下来。光弹性应力冻结模型试验正是利用有机化合物的这种特性，实现对处于复杂环境中的模型内部应力规律进行观测。

升温过程会伴随着材料软化，试验模型体积又较大，为了控制模型整体软化过程较为均匀，通过对模型周边温度传感器的实时监测，升降温过程确保模型内部最大温差小于10 ℃，冻结应力温度控制曲线如图7所示。

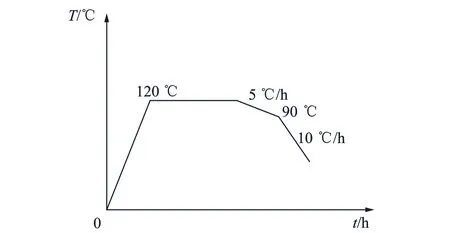
图7 冻结应力温度控制曲线Fig.7 Temperature control curve of freezing stress

模型应力冻结后进行切片，切片厚度9.8 mm左右，横向切片为H1～H5，纵向切片为Z11～Z68，切片方案如图8所示。

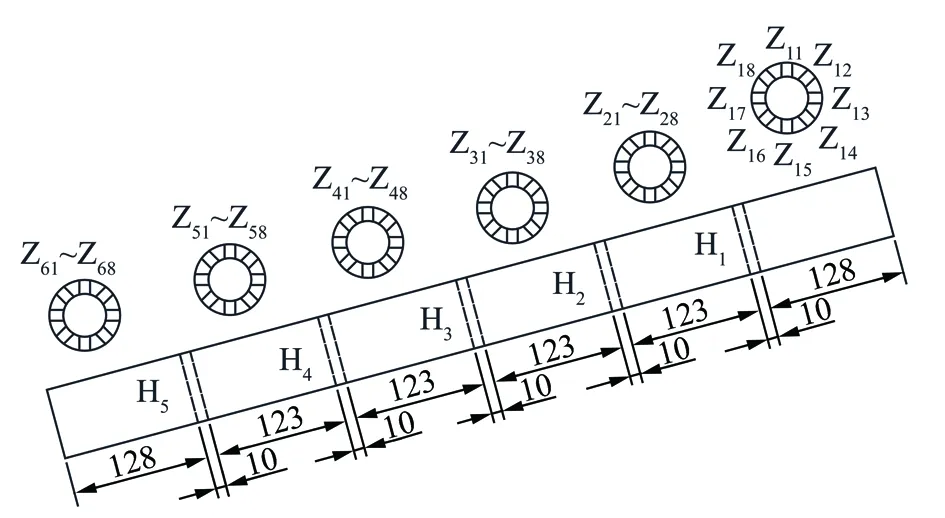
图8 模型切片方案Fig.8 Model slices scheme

4 结果分析

利用TST-500型光弹仪对冻结应力后切片作正射分析，采用高分辨率CCD摄像头作等差线条纹图像的采集、记录，经图像数字处理和原型应力换算，最终提供处理后的应力分析结果。图9提供了典型横向切片的等差线条纹图。经条纹细化处理后横向切片的最大剪应力等值线分布如图10所示。表4为切片剪应力计算值，表中τ1为切片内模型最大剪应力，τ2对应应力换算后原型最大剪应力。

通过对比模型不同深度横向切片最大剪应力等值线图发现，最大剪应力均出现在模型两帮内缘位置，局部增高的最大剪应力水平随与峰值剪应力点的距离增加由内缘向外缘呈现弧形衰减;模型两帮应力集中水平远高于顶底位置，而顶部最大剪应力又大于底部;随埋深增加，不仅模型内部应力数值有所增大，应力不均匀程度也随之提高，在模型顶部区域尤为明显，H1切片顶部2、3级等差条纹连同至模型两帮，而埋深较深位置的切片H2、H3顶部等差条纹环向延伸区域较小，这与斜井荷载不均匀性随深度而增加的理论分析结果相吻合[10]。结合D2分布式压力传感器数据，得到H3切片外缘法向应力与内缘环向应力随环向角度变化曲线，由于左右对称性较好，取右半侧分析，定义顶部环向角度为0°，如图11所示。模型外缘最大法向应力出现在井筒顶部位置，随着环向角增加至90°过程中逐步减小，伴随环向角进一步增加至180°，井筒外缘法向应力开始增大，井筒上半部法向应力大于下半部。井筒内缘环向应力最大值出现在环向角70°～115°，顶底位置环向应力值较小。

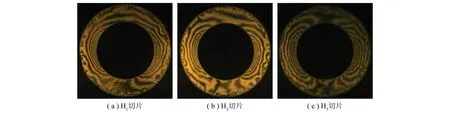
图9 钠光下横向切片等差线条纹Fig.9 Isochromatic lines of transverse section in sodium light

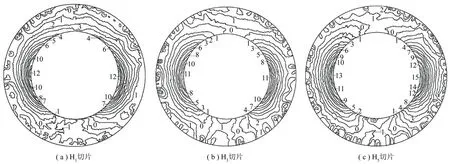
图10 横向切片内最大剪应力等值线分布Fig.10 Maximum shear stress distribution of transverse section

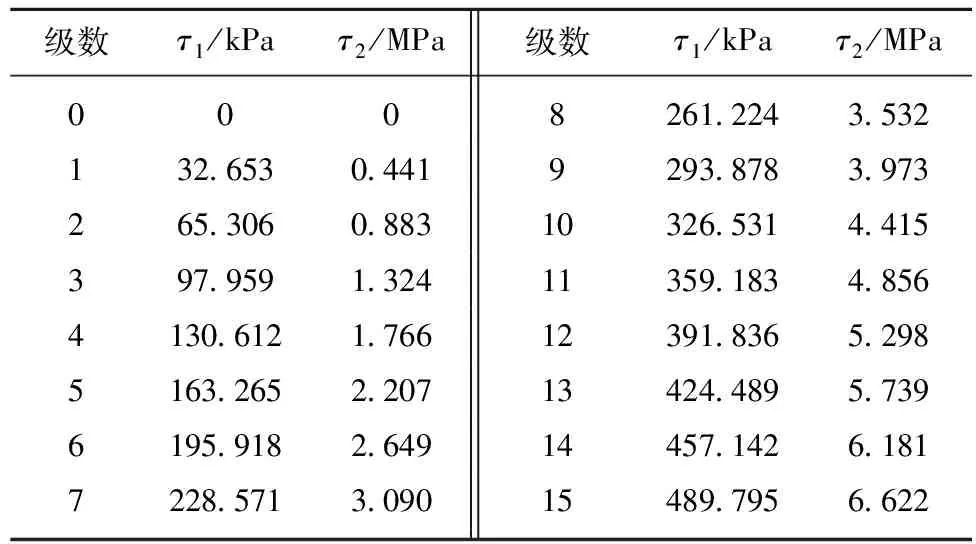
级数τ1/kPaτ2/MPa级数τ1/kPaτ2/MPa000826122435321326530441929387839732653060883103265314415397959132411359183485641306121766123918365298516326522071342448957396195918264914457142618172285713090154897956622

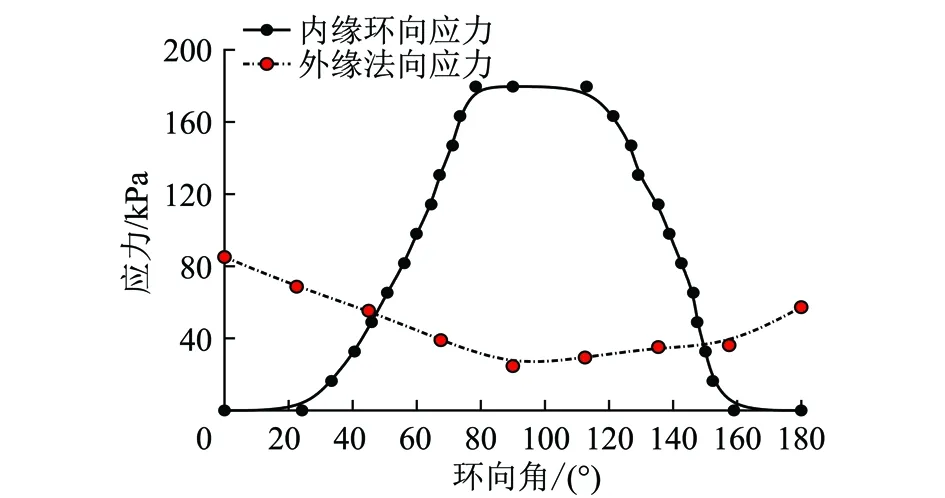
图11 H3切片内缘环向应力和外缘法向应力随环向角变化Fig.11 Distribution of hoop stress of the inner edge and normal stress of the out edge with the circumferential angle in H3 section

图12为典型纵向切片的等差线条纹图。模型纵向切片剪应力梯度总体较为平缓，无明显应力集中区，随埋深增加，等差条纹级数近似线性增大，试验结果也验证了所采用加载方式的稳定性和有效性。模型纵向切片的最大剪应力等值线受埋深和环向角度变化影响较大，在埋深较浅处，模型顶部位置切片Z21内最大剪应力变化梯度大于两帮位置切片Z23，最大剪应力值大于底部位置切片Z25;在埋深较深处，模型顶部位置切片Z41内最大剪应力变化梯度小于两帮位置切片Z43，最大剪应力值依旧大于底部位置切片Z45。

图12 白光下纵向切片等差线条纹Fig.12 Isochromatic lines of longitudinal section in white light

5 结 论

(1)自行设计了厚砂土层斜井井壁三维光弹试验系统，通过应力冻结切片测试结果获得了斜井井筒模型的全场最大剪应力等值线分布状态，给出了应力集中位置、峰值应力水平及其衰减状态，直接显示了斜井井壁各区域的实际强度裕度，反映了斜井井筒强度特征和强度薄弱位置。

(2)斜井井壁应力分布沿环向有较大不均匀性，横向截面最大剪应力远大于纵向截面，顶部最大剪应力大于底部，最大剪应力集中区出现在两帮内缘水平面±25°范围内，是斜井井壁设计的重点校核位置。

(3)随井筒埋深增加，井壁纵向应力近似线性增加，不同环向位置应力增加速率存在差异，从而导致不同埋深井筒的应力分布规律和不均匀性也有所区别，在斜井井壁精细化设计中，可对不同埋深井筒采用针对性设计。

[1] 宋洪柱.中国煤炭资源分布特征与勘查开发前景研究[D].北京:中国地质大学,2013. SONG Hongzhu.Study on the distribution characteristics and the exploration and development prospect of coal resource of China[D].Beijing:China University of Geosciences,2013.

[2] 周国庆，程锡禄.特殊地层中的井壁应力计算问题[J].中国矿业大学学报,1995，24(4):24-30. ZHOU Guoqing,CHENG Xilu.Study on the stress calculation of shaft lining surrounded by special strata[J].Journal of China University of Mining & Technology,1995,24(4):24-30.

[3] 蒋斌松.复合井壁的弹性分析[J].煤炭学报,1997,22(4):397-401. JIANG Binsong.Elastic analysis of the composite shaft linings[J].Journal of China Coal Society,1997,22(4):397-401.

[4] 蒋斌松.立井井壁的计算理论[J].岩石力学与工程学报,2003,22(S1):2183-2186. JIANG Binsong.Calculating theory of shaft lining[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(S1):2183-2186.

[5] 周扬,周国庆.考虑治理荷载作用时井壁严格轴对称变形分析[J].岩土工程学报,2008,30(7):999-1004. ZHOU Yang,ZHOU Gouqing.Strict axisymmetric deformation analysis of shaft linings considering shaft-curing load[J].Chinese Journal of Geotechnical Engineering,2008,30(7):999-1004.

[6] 周晓敏,陈建华,罗晓青.孔隙型含水基岩段竖井井壁厚度拟订设计研究[J].煤炭学报,2009,34(9):1174-1178. ZHOU Xiaomin,CHEN Jianhua,LUO Xiaoqing.Research on the preliminary thickness design of shaft lining in porous rock aquifer[J].Journal of China Coal Society,2009,34(9):1174-1178.

[7] 周扬,周国庆.塑料板夹层双层井壁的轴对称变形分析[J].煤炭学报,2010,35(9):1470-1475. ZHOU Yang,ZHOU Gouqing.Axisymmetric deformation analysis for the double layer shaft with a plastic interlayer[J].Journal of China Coal Society,2010,35(9):1470-1475.

[8] 中国煤炭建设协会.煤矿斜井井筒及硐室设计规范[S].北京:中国计划出版社,2007.

[9] 张荣立,何国纬,李铎.采矿工程设计手册(中册)[M].北京:煤炭工业出版社,2003.

[10] 周檀君,周国庆,王建州,等.煤矿长斜井井筒外荷载特征研究[J].煤炭工程,2016,48(3):77-80. ZHOU Tanjun,ZHOU Guoqing,WANG Jianzhou,et al.External load characteristics of long inclined shaft in coal mine[J].Coal Engineering,2016,48(3):77-80.

[11] 王襄禹,柏建彪,高 祥.斜井在表土段时底板承载力的初探[J].能源技术与管理,2004(3):16-18. WANG Xiangyu,BAI Jiangbiao,GAO Xiang.Preliminary research to the floor load- bearing capacity of slope within overburden soil[J].Energy Technology and Management,2004(3):16-18.

[12] 赵峰.壁后注浆技术在大佛寺煤矿斜井中的应用研究[D].西安:煤炭科学研究总院西安分院,2006. ZHAO Feng.The application study of the wall grouting behind technique at manage the inclined well of Dafosi coal mine[D].Xi’an:Xi’an Branch of CCRI,2006.

[13] 闫振东,杨仁树,岳中文,等.渗水厚砾石层斜井围岩破坏机理模型试验[J].煤炭学报,2009,34(12):1599-1604. YAN Zhendong,YANG Renshu,YUE Zhongwen,et al.Model test on failure mechanism of the surrounding rock of oblique laneway in thick gravel stratum under seepage water[J].Journal of China Coal Society,2009,34(12):1599-1604.

[14] 岳中文,杨仁树,孙中辉,等.富水厚砾石层斜井围岩破坏机理试验研究(Ⅱ)[J].煤炭学报,2010,35(8):1273-1278. YUE Zhongwen,YANG Renshu,SUN Zhonghui,et al.Test study on failure mechanism of the surrounding rock of inclined shaft in thick gravel stratum with abundant water(Ⅱ)[J].Journal of China Coal Society,2010,35(8):1273-1278.

[15] 王卫军，袁越，余伟健，等.采动影响下底板暗斜井的破坏机理及其控制[J].煤炭学报,2014,39(8):1463-1472. WANG Weijun,YUAN Yue,YU Weijian,et al.Failure mechanism of the subinclined shaft in floor under mining influence and its control[J].Journal of China Coal Society,2014,39(8):1463-1472.

[16] 周檀君，周国庆.考虑倾角作用的斜井冻结壁厚度计算方法[J].中国矿业大学学报，2016,45(3):514-520. ZHOU Tanjun,ZHOU Guoqing.Calculation method of frozen soil wall thickness for inclined shaft in consideration of the shaft inclination[J].Journal of China University of Mining & Technology,2016,45(3):514-520.

[17] Narasimhamurty T S.Experimental methods of determining the photoelastic constants[M].Photoelastic and Electro-Optic Properties of Crystals.Springer US,1981:197-297.

[18] 冯琼,许蔚,李俊昌,等.改进的数字全息光弹方法-理论研究[J].工程力学,2012,29(9):56-59. FENG Qiong,XU Wei,LI Junchang,et al.Research on the improvement of digital holographic photo-elastic method[J].Engineering Mechanics,2012,29(9):56-59.

[19] 马险峰,孔令刚,方薇,等.砂雨法试样制备平行试验研究[J].岩土工程学报,2014,36(10):1791-1801. MA Xianfeng,KONG Linggang,FANG Wei,et al.Parallel tests on preparation of samples with sand pourer[J].Chinese Journal of Geotechnical Engineering,2014,36(10):1791-1801.

[20] 徐光明,章卫民.离心模型中的粒径效应和边界效应研究[J].岩土工程学报,1996,18(3):80-85. XU Guangming,ZHANG Weimin.A study of size effect and boundary effect in centrifugal tests[J].Chinese Journal of Geotechnical Engineering,1996,18(3):80-85.

[21] Cernosek J.Three-dimensional photoelasticity by stress freezing[J].Experimental Mechanics,1980,20(12):417-426.

Three-dimensionalphotoelasticitymodeltestofinclinedshaftonstressdistributioninthicksandsoillayer

ZHOU Tanjun1,ZHOU Guoqing1,LIAO Bo1,2，ZHANG Haiyang1，LAI Zejin1，TAO Xiangling1,3

(1.StateKeyLaboratoryforGeomechanicsandDeepUndergroundEngineering,ChinaUniversityofMining&Technology,Xuzhou221008,China; 2.DepartmentofTechnologyandEngineeringManagement,ZhejiangGongshangUniversity,Hangzhou310018,China; 3.CollegeofEnergyandTransportationEngineering,JiangsuVocationalInstituteofArchitecturalTechnology,Xuzhou221116,China)

Taking the main inclined shaft of a coal mine across thick sandy soil layer as the engineering case,established a physical model for the inclined shaft wall with the three-dimensional stress-freezing photoelastic method.A three-dimensional simulation for the stress of inclined shaft wall across thick sandy soil layer was made under the consideration of inclined roadway inclination.The whole-field maximum shear stress contour map was obtained from the stress-freezing photoelastic test and the changes of shaft wall stress in relation to shaft depth and circumferential angle were also analyzed.According to the results,the internal stress and its uneven distribution of the transverse section of shaft wall were much greater than that of the longitudinal section.The maximum shear stress centered on the inner edges of shaft wall sides at a range of ±25°.The maximum shear stress on the top of inclined shaft wall was larger than the bottom.With the increase of shaft depth,the longitudinal stress showed a near-linear increase,but the rates of increase in relation to different circumferential angles differed greatly.Thus,the size and distribution of shaft wall internal stress varied with different shaft depth.

inclined shaft;model test;stress distribution;frozen stress method

10.13225/j.cnki.jccs.2017.0357

TD265.3

:A

:0253-9993(2017)08-1979-08

国家自然科学基金资助项目(51104146);国家高等学校学科创新引智计划(111)资助项目(B14021)

周檀君(1989—)，男，浙江金华人，博士研究生。E-mail:tanjunzhou@126.com

周檀君，周国庆，廖波，等.厚砂土层斜井井壁应力分布规律三维光弹性模型试验[J].煤炭学报,2017,42(8):1979-1986.

ZHOU Tanjun,ZHOU Guoqing,LIAO Bo,et al.Three-dimensional photoelasticity model test of inclined shaft on stress distribution in thick sand soil layer[J].Journal of China Coal Society,2017,42(8):1979-1986.doi:10.13225/j.cnki.jccs.2017.0357