内壁粗糙碗中的动力学问题深度探究(二)

倪 峰(德清县高级中学 浙江 湖州 313200)

内壁粗糙碗中的动力学问题深度探究(二)

倪 峰
(德清县高级中学 浙江 湖州 313200)

为更深入探究内壁粗糙碗中的动力学问题，利用Mathematica数学软件计算和画出了物体逆时针运动的角度θ与运动时间t的图像关系和物体逆时针运动的角速度ω与运动时间t的图像关系，从图像关系可以准确得到在某时刻对应的角度、角速度、速度.

内壁粗糙的碗 竖直轨道 动力学 二阶非线性常微分方程 Mathematica

具体模型如图1所示，物体(可看成质点的物体)在内壁粗糙的碗中从A点向下逆时针下滑，物体与粗糙内壁的动摩擦因数为μ.

图1 情境图

从A点下滑到第一次速度为零的位置的整个过程，物体受到3个力的作用，分别是重力mg，摩擦力Ff，支持力FN.除重力外，其他两个力都是变力.在文献[1]中，笔者推导出物体逆时针运动的角速度ω与转过的角度θ的函数关系，即给出了ω与θ的解析解

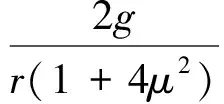
并利用Excel画出了ω与θ的图像关系，可以得到物体在粗糙碗中从A点下滑做逆时针圆周运动到第一次速度为零这个过程，轨道上各个位置所对应的角速度和速度.那么，θ与t，ω与t之间又有什么关系呢？

1 小球在粗糙内壁逆时针下滑的θ与t及ω与t的解析解

根据推导得出的ω与θ的解析解

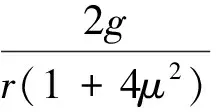
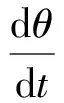
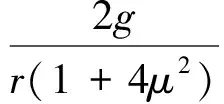
(1)

对式(1)两边积分得

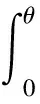
(2)

式(2)比较复杂，笔算无法推导θ与t的解析解和ω与t的解析函数.

2 利用Mathematica数值解法画出θ-t和ω-t图像

取g=9.8 m/s2，r=1 m.分别画出μ=0，0.1，0.5，0.8时，θ与t，ω与t的图像，具体编程如下所示：

Quit

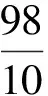
PlotStyle0={{Red,Thickness[0.015]},{Green,

Thickness[0.015]},{Black,Thickness[0.015]},{Blue,

Thickness[0.015]},{Purple,Dashing[{0.01,0.05,0.01}],Thickness[0.005]},{Green,Dashing[{0.01,

0.02,0.05}],Thickness[0.005]}};θf[μ_]:=

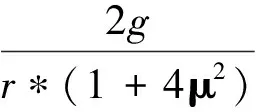
((1-2μ2)Sin[θ]+3μCos[θ]-3μExp[-2θ]))-1/2,{ θ,0, θθ}]

fig[μ_,style_]:=ParametricPlot[{Re[tjie[,θθ]],θθ},{θ,0,θf[μ]},PlotStyle→PlotStyle0[[style]],

AxesLabel→{ "t","θ"},BaseStyle→{Large},AxesStyle→Arrowheads[0.06],RotateLabel→True,PlotRange→All,AxesOrigin→{0,0}]

figA[μ_,style_]:=ParametricPlot[{Re[tjie

3μCos[θθ]-3μExp[-2μθθ]))1/2},{θθ,0, θf[μ]},

PlotStyle→PlotStyle0[[style]],AxesLabel→{"t","dθ/dt"},BaseStyle→{Large},AxesStyle→Arrowheads[0.06],RotateLabel→True,PlotRange→

All,AxesOrigin→{0,0}]

"μ=0,t[0]" →tjie[0,0.0001]"μ=0.1,t[0]" →tjie[0.1,0.0001]

"μ=0.5,t[0]" →tjie[0.5,0.0001]

"μ=0.8,t[0]" →tjie[0.8,0.0001]

"μ=0, θf"→f[0]

"μ=0.1, θf"→θf[0.1]

"μ=0.5, θf"→θf[0.5]

"μ=0.8, θf"→θf[0.8]

μ=0,t[0] →0.00451754

μ=0.1,t[0] →0.00451755

μ=0.5,t[0] →0.0045176

μ=0.8,t[0] →0.00451763-2.36667

μ=0, θf→3.14159

μ=0.1, θf→2.67214

μ=0.5, θf→1.72223

μ=0.8, θf→1.33753

写完倒数第二行程序后，按Shift+Enter运行，得到角度θ与时间t的图像，如图2所示.从图2可以得到，物体在粗糙碗中从A点下滑做逆时针圆周运动到第一次速度为零这个过程，某时刻物体对应在轨道上的位置.写完最后一行程序后，按Shift+Enter运行，得到角速度ω与时间t的图像，如图3所示.从图3可以得到，物体在粗糙碗中从A点下滑做逆时针圆周运动到第一次速度为零这个过程，某时刻物体对应的角速度.

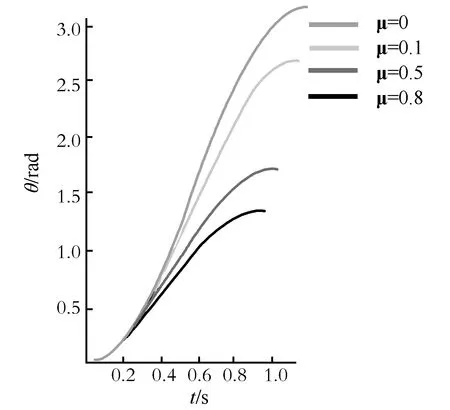
图2 角度θ与时间t的关系

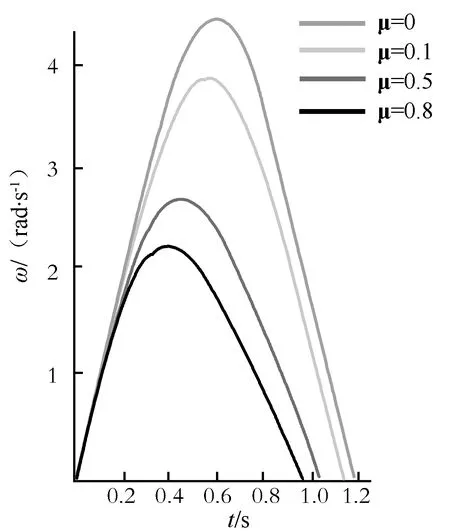
图3 角速度ω与时间t的关系

在具体应用过程中，对应不同的动摩擦因数μ，求不同时刻对应的角度和角速度，只需要在程序当中改变μ这个参数的大小即可，然后再按Shift+Enter运行，就能得到相应的图像关系.若读者需要以上程序，或进行学术交流，可直接与笔者联系.

1 程守洙，江之勇．普通物理学2(第5版)．北京：高等教育出版社,2003.25～28

2 马文蔚．物理学(第3版)．北京：高等教育出版社，1994.5～203 董键.Mathematica与大学物理计算(第2版). 北京：清华大学出版社，2010

In-depthResearchontheDynamicIssueinRoughBowlWall(II)

Ni Feng
(Deqing Senior high school, Huzhou, Zhejiang 313200)

The author deduced the relationships between angular velocity ω and angle of turn θ and drew the picture of ω with θ in the in-depth dynamic research in rough bowl wall(I). We can get corresponding ω and velocity v in the different orbit positions when the object rolls down from A point in the rough bowl wall to the position with zero velocity for the first time. In order to research the dynamic in rough bowl wall deeply, in this paper we calculate and draw the pictures of θ with t and ω with t by Mathematica when the object do anticlockwise motion. We can get corresponding θ, ω and v accurately in different time from the pictures.

rough bowl wall; a vertical track； dynamic; the second order ordinary differential equation；mathematica

2016-08-29)