界面自由度柔性等效与子结构频响函数综合方法

张 勇， 侯之超， 赵永玲

(清华大学 汽车安全与节能国家重点实验室，北京 100084)

界面自由度柔性等效与子结构频响函数综合方法

张 勇， 侯之超， 赵永玲

(清华大学 汽车安全与节能国家重点实验室，北京 100084)

针对频响函数子结构综合法中由于转角自由度频响函数缺失造成的综合建模误差较大的问题，提出了界面自由度柔性等效方法。将界面分为若干子界面，假定子界面刚性，通过最小二乘坐标变换，提取可描述子界面特征的6自由度分量，据此实现对子界面的刚性等效，综合所有子界面的等效自由度即形成界面的柔性等效。利用等效后的界面柔性自由度与原界面自由度的关系，对子结构的原始频响函数进行相应地变换，并将其应用到子结构频响函数综合方法中。仿真结果表明，将界面自由度进行柔性等效能明显提高频响函数的综合精度。

频响函数子结构综合；界面自由度；柔性等效

与模态综合方法相比，频响函数子结构综合方法直接利用子结构频响函数进行综合建模，无需考虑主模态个数的限制和剩余模态等问题，只需获得所感兴趣的频段内完整的频响数据即可，适合模态密集与阻尼较大结构的综合建模[1-2]。但界面自由度信息的完整性一直是频响函数子结构综合法面临的一个重要困难，尤其在频响函数测试中，有关转角自由度的频响信息一般难以准确获得。除少数特殊连接界面外，例如球铰，其在连接界面上无转矩与转角自由度响应，无需考虑与转角自由度有关的频响，对其它一般结构件来说，连接界面大都承受弯矩，在连接界面上有转角位移响应，这时转角自由度的频响信息就十分重要。

Silva等[3]指出完整的频响函数矩阵至少包含了75%的转角自由度的频响信息。Liu等[4]论述了转角自由度在频响函数子结构综合方法中的重要性，指出不考虑转角自由度会得到错误的综合结果。有关子结构综合建模的商用软件中也未见考虑与转角自由度相关的频响函数[5]。为了得到转角自由度的频响特性，众多学者进行了研究，其中主要集中对转角自由度频响的间接测量方法的探究，如通过附加“T”形块等进行弯矩激励和转角自由度响应的间接测量。但其因测量引起的误差仍较大。模态缩聚与扩展技术也被用来对未测量自由度的频响函数进行补偿，Avitabile等[6]考虑剩余留数的影响，利用系统等效缩聚与扩展(SEREP)方法直接估计未测频响函数，扩展频响函数矩阵，该方法需要获取结构的模态信息。Van Der Seijs等[7]使用标准替代部件与未知子结构先行综合，然后利用子结构解耦方法得到未知子结构的界面信息。标准替代部件的设计、制造显然增加了综合建模的成本与难度。De Klerk等[8]提出一种等效多点连接方法(EMPC)的方法，将连接界面视为刚性面，按刚体运动理论对界面进行刚性等效：将界面自由度变换成关于一个虚拟点的6自由度，这6个自由度中包含了界面3个转角自由度，并利用这种变换关系对原频响函数进行“滤波”。该方法在部分分析频带，能改进频响函数的综合效果。

为进一步提高在缺失转角自由度频响信息时的子结构综合精度，本文考虑将界面分块，将分块后的子界面依次利用EMPC方法进行刚性等效，每个子界面自由度包含可描述其子界面刚体运动的6个自由度分量，综合所有子界面刚性等效后的自由度即形成整体界面的柔性等效自由度，相应地，利用等效后的界面柔性自由度与原始界面自由度的变换关系，对子结构的原始频响函数进行扩充，实现对界面弹性特性的表征。

1 EMPC理论

1.1界面自由度等效变换

据经典的Jetmundsen子结构频响综合方法，两子结构a,b综合后的频响函数Hab可写成[9]：

(1)

式中:H为频响;上标a,b,ab分别表示子结构a,b与综合后的结构ab;下标i，c分别表示子结构的内部与界面自由度。完整的界面信息应包含界面节点平动与转动自由度的全部频响函数，即c中应包含转角自由度。

子结构a的频率响应方程为

(2)

uc=Rueq+μ

(3)

为方便起见，上式省略上标a。类似模态综合法的坐标变换，ueq可视为界面主自由度响应，μ为剩余自由度响应，R则描述了该界面的主模态信息。子结构的所有自由度响应可写成：

(4)

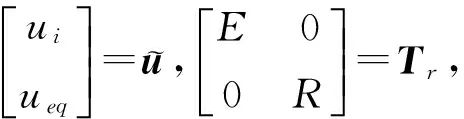
(5)

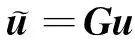
(6)

将式(2)写成u=Hf，并左乘G可得

Gu=GHf

(7)

引入下式：

GT(GT)+=E

(8)

Gu=GHGT(GT)+f

(9)

考虑式(6)，上式最后可简写成：

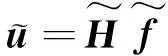
(10)

1.2界面自由度的刚性等效

(11)

(12)

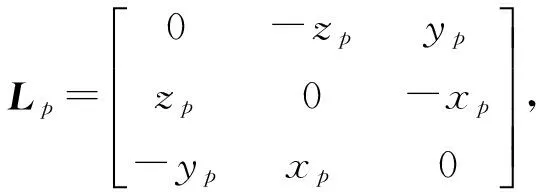
(13)

(14)

2 界面自由度的柔性等效

(15)

(16)

式中:Bi为布尔矩阵，其元素为0或1;Ri为R1的子矩阵，uci为uc的子矩阵即

Ri⊂R1，uci⊂uc

(17)

(18)

考虑子结构内部与界面自由度，整体变换矩阵G可写成：

(19)

代入式(10)即可得到变换后的频响函数。从模态理论的角度看EMPC仅考虑界面的刚体运动，而界面柔性等效方法由于对界面进行了分块等效，所以还考虑了界面的高阶弹性运动，可视为EMPC的高阶等效。

以图1结构为例，简要说明界面柔性等效方法中变换矩阵与布尔矩阵的构成。该结构由子结构Sub_a

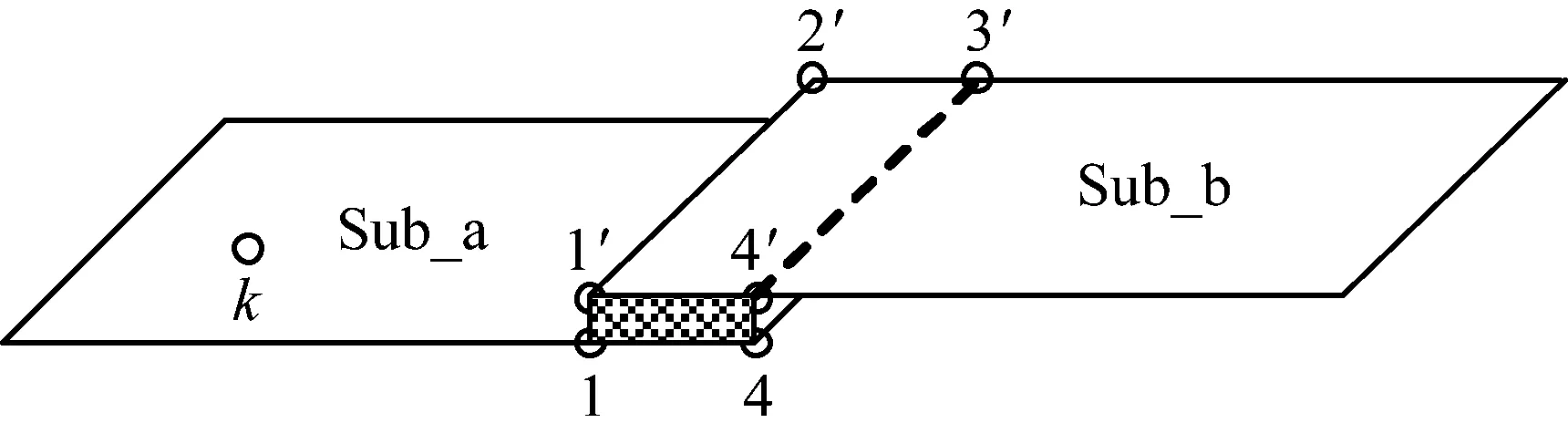
图1 两子结构综合示意图

与Sub_b组成，其连接界面为1～4与1′～4′节点构成的平面，两子结构在界面处完全固接，假定节点1～4与1′～4′为界面测点，内部测点k，每个测点仅包含3个平动自由度。

以子结构Sub_a为例，将其界面分为由{1,2,3}，{1,2,4}，{1,3,4}，{2,3,4}节点所构成的4个子界面，以第二组{1,2,3}为例，图1下所示，其界面自由度的变换矩阵与布尔矩阵可写成：

(20)

其它变换矩阵与布尔矩阵可类似写出。最后综合界面测点自由度、界面整体刚性等效自由度与4组子界面的柔性自由度，代入式(19)可得到界面自由度柔性等效后的子结构变换矩阵：

(21)

将式(21)代入式(10)可得到变换后的频响函数。一般来说仅利用3个节点的平动自由度就能描述界面的刚体转动自由度，但有时界面自由度等效后依然不能完全描述整个界面的性质，例如界面上的点全部在一条直线上，这时可增加靠近界面节点的自由度，联合描述界面信息，也即界面自由度uc为可包含靠近界面节点自由度的一类广义自由度。

界面自由度柔性等效方法，与有限元思想类似，界面细化程度越高，也即有限元中的单元越密集，界面描述越精确，越能反应界面的柔性特征。但在实际应用中，受界面大小，实验条件限制，不可能将子界面分割的过细。界面划分越细意味着需要在界面布置更多测点，对于需要通过实验进行频响测试的子结构来说，需要在实测结构界面上(或者靠近界面连接位置)适当增加传感器数目。根据式(3)界面自由度等效方程知，若子界面完全刚性，根据刚体运动的特点，则剩余自由度响应μ趋近于零(由于变换矩阵R忽略了高阶小量，μ不等于零而是趋近于零)，所以可通过剩余自由度响应μ值的大小判断子界面大小是否合理。事实上，我们通常感兴趣的是低频带的结果，有限个刚性子界面，就足以描述低频带内的界面特性。

3 数值仿真

算例1

为验证本文所提出的方法，将一悬臂板结构分割为两子结构，之后重新将两子结构在界面处进行焊接，利用频响函数子结构综合方法进行建模，并与分割前的整块悬臂板结构的频响函数计算结果进行对比分析。

悬臂板结构尺寸为80×20×2，分割后悬臂板结构Sub_a，以及自由板结构Sub_b，图2，两板结构尺寸均为40×20×2，Sub_a的界面为节点1～3所在的直线，Sub_b的界面为1′～3′所在的直线。假定测点仅布置在1～3点和1′～3′点，参与计算的Sub_a的界面自由度包括1～3节点的3个方向的平动，内部自由度为5节点z向平动；参与计算的Sub_b的界面自由度为1′～3′节点的3个方向的平动，内部自由度为5′节点z向平动。

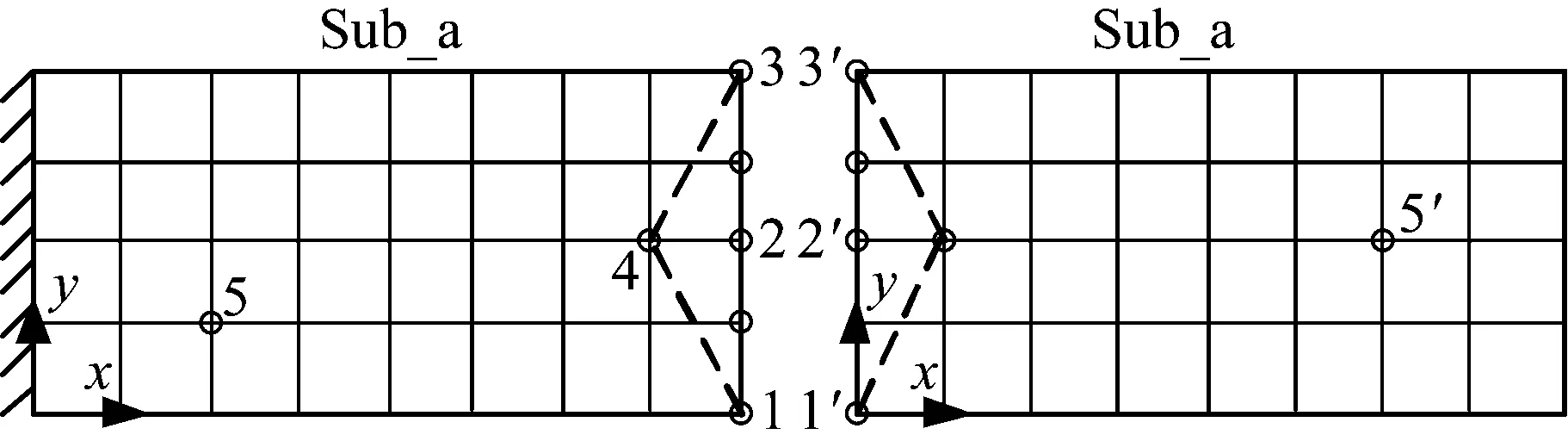
图2 悬臂板子结构综合示意图

图3与图4给出了方法a与b综合后结果对比，分析发现，忽略界面转角自由度信息得到的频响与参考频响有较大差别。方法b得到的H55第一阶幅值频率为115 Hz，而参考频响为40 Hz，相位也有的较大差别。这是因为界面缺少转角位移约束，综合求解时，相当于两个子结构在界面铰接而非焊接。另外在728 Hz与2 412 Hz左右，两种方法综合得到的频响吻合较好，这是因为该频率下界面铰接与焊接的结构模态近似一致。

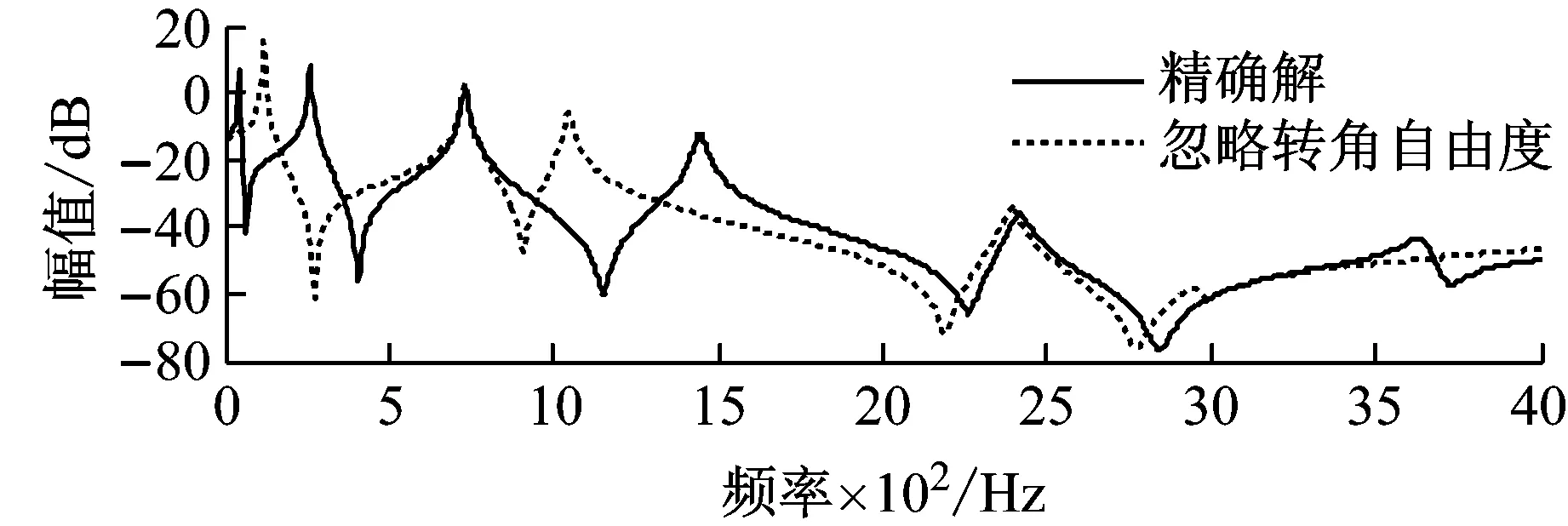
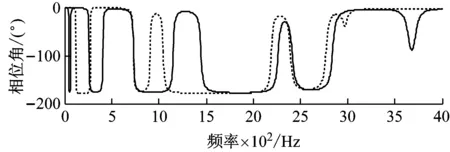
图3 H55幅值与相位对比(方法a，b)

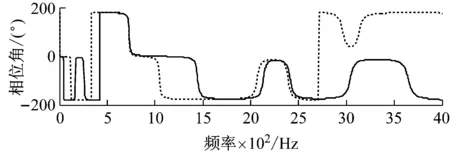
图4 H5′5幅值与相位(方法a，b)

图5、6给出了4种方法的综合对比结果，可以发现，界面自由度刚性等效方法比不考虑转角自由度的方法有所改进，但得到的第一与第四阶的幅值频率与参考值仍然有一定差距；而在3 000 Hz以内，利用界面自由度柔性等效方法得到频响、相位，与参考频响、相位基本一致，显示了界面自由度柔性等效方法在子结构综合方法中的具有较高精度。在本算例中仅在界面附近增加了一个测点，若还需得到3 000 Hz以后的更高频的精确结果，则可通过增加测点，也即增加子界面的个数来提高综合精度。

图5 H55幅值与相位对比(方法a～d)

图6 H5′5幅值与相位对比(方法a～d)

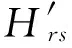
图7 H55、H5′5频响幅值(噪声σ%=1%)

从图7与图8中可看出，加入噪声后得到的频响在前两阶频率有所漂移，反共峰处幅值误差较大。总体来看频响函数在噪声较小时误差较小，能得到比较好的综合结果；噪声稍大时误差有所增大，但总体趋势一致。其原因在于对频响函数求逆时，噪声被放大。这是基于频响函数综合方法不可避免的问题[10]。

算例2

为分析车轮至车身的振动传递特性，采用频响函数综合方法，对白车身与前悬进行综合建模，计算制动盘中心至车身座椅安装点即目标响应点的频响。

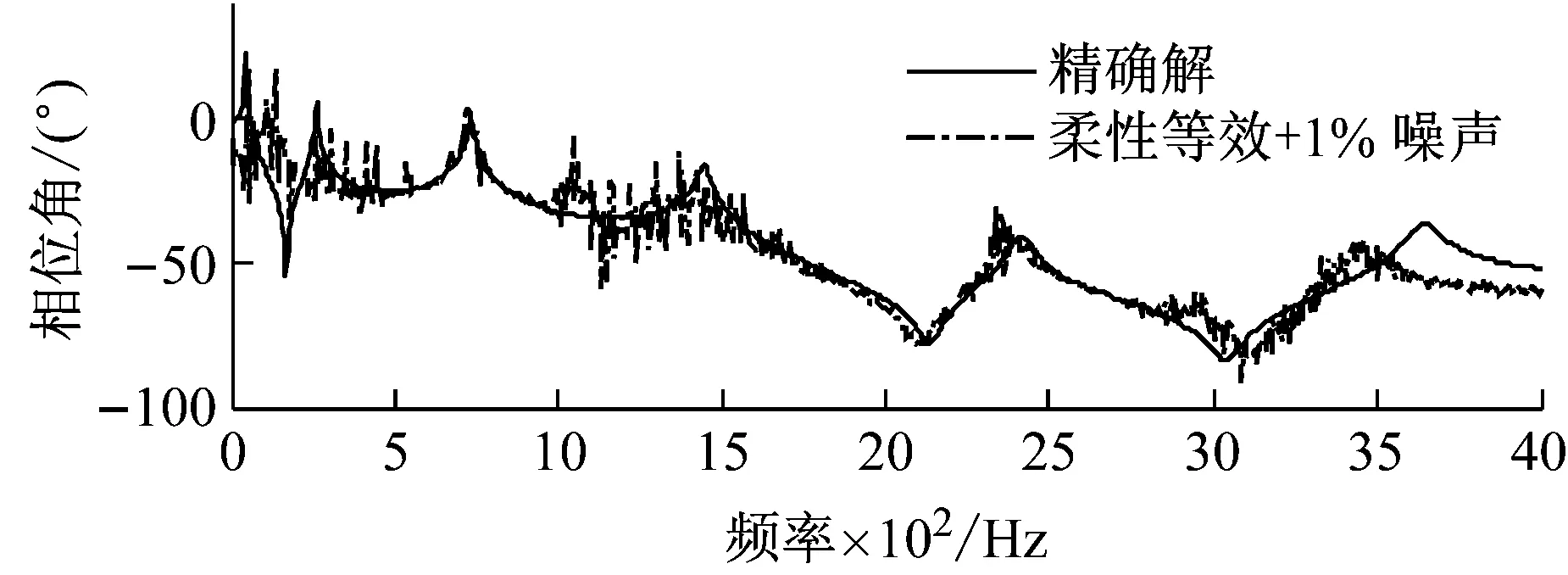
图8 H55、H5′5频响幅值(噪声σ%=5%)

建立1/2白车身模型，图9所示，作为子结构a；不带轮胎与横臂等右前悬模型，图10，作为子结构b。为便于计算，对两个子结构模型均进行了适当简化。右前悬与白车身通过3组螺栓连接，连接界面为螺栓孔周，图12，综合后的结构如图11。

图9 1/2车身模型(子结构a)

图10 右前悬模型(子结构b)

图11 综合后的模型

图12 悬架侧界面测点

分别在车身与悬架侧的螺栓孔周边布置相应测点，图12所示。同算例1，采用4种方法进行频响函数综合建模。计算制动盘中心至车身座椅安装点处的频响：a：直接有限元建模计算，作为频响计算结果的参考值；b：每个螺栓孔周选取一个测点，忽略界面转角自由度，仅利用每个测点的平动自由度参与计算；c：为描述界面转角自由度，每个螺栓孔周选取4个测点，将两个子结构的界面自由度进行刚性等效，利用等效后的频响参与计算；d：每个螺栓孔周选取4个测点，将界面自由度进行柔性等效，利用等效后的自由度进行频响函数综合分析。

图13、14给出了采用4种方法综合计算获得的制动盘中心至车身座椅安装点x与z向频响。其中，不考虑界面转角自由度计算得到的频响函数误差较大，尤其在频率较高时。刚性与柔性两种方法获得z向频响基本一致，这主要是因为螺栓孔周，界面刚度较大，3个连接界面表现为刚性。但从250 Hz开始，采用刚性等效方法计算的x向频响也出现了偏差，图13。而在整个分析带宽内，采用界面柔性等效方法计算得到的频响与精确解一致，进一步显示了界面自由度柔性等效方法能显著提高频响函数子结构综合精度。

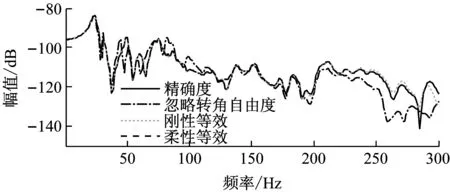
图13 制动盘中心至车身座椅安装点x向频响

图14 制动盘中心至车身座椅安装点z向频响

从上面两个算例中可见，采用界面柔性等效的频响函数子结构方法，能获得更高的综合精度。另外考虑界面自由度柔性等效方法在高频依然有良好的综合效果，可利用这一优点提高涉及结构-声传递路径的综合建模精度。

4 结 论

考虑到频响函数子结构综合法中，转角自由度的频响信息一般难以准确获得，造成了综合建模误差较大的问题，提出了界面自由度柔性等效方法，并将其应用到频响函数子结构综合方法中。仿真结果表明，本文所提出的界面柔性等效方法能明显改善子结构频响函数综合效果。

[1] 吴家驹, 张宇光. 基于实测频响函数的子结构模态综合[J]. 应用力学学报, 1992(3):36-43.

WU Jiaju, ZHANG Yuguang. Substructures mode synthesis based upon measured frequency response function[J].Chinese Journal of Applied Mechanics, 1992(3):36-43.

[2] 王威. 基于频响函数的子结构混合建模研究及实现[D]. 武汉：华中科技大学, 2012.

[3] SILVA J M M, MAIA N M M, RIBEIRO A M R. Indirect estimation of rotational frequency response functions[C]//Proc of the 19th International Modal Analysis Conference. Orlando: IMAC. 2001, 1542.

[4] LIU W, EWINS D. Importance of assessment of RDOF in FRF coupling analysis[C]//Proceedings of the 17th International Modal Analysis Conference, Society for Experimental Mechanics, Bethel, CT, Feb. 1999, 1481-1487.

[5] A Siemens business. FRF-Based Substructuring (FBS) Case Tutorial[OL]. LMS virtual lab online help, 2013.

[6] O′CALLAHAN A P. Frequency response function expansion for unmeasured translation and rotation DOFS for impedance modelling applications[J]. Mechanical Systems and Signal Processing, 2003, 17(4): 723-745.

[7] VAN DER SEIJS M V, DE KLERK D, RIXEN D J, et al. Validation of current state frequency based substructuring technology for the characterisation of steering gear-vehicle interaction[C]//Topics in Experimental Dynamic Substructuring, Volume 2: Proceedings of the 31st IMAC, A Conference on Structural Dynamics, 2013. Springer Science & Business Media, 2013, 36: 253-266.

[8] DE KLERK D, RIXEN D, VOORMEEREN S, et al. Solving the RDoF problem in experimental dynamic sub-structuring[C]. 26th International Modal Analysis Conference (IMAC XXVI), Orlando, FL. 2008.

[9] JETMUNDSEN B, BIELAWA R L, FLANNELLY W G. Generalized frequency domain substructure synthesis[J]. Journal of the American Helicopter Society, 1988, 33(1): 55-64.

[10] NICGORSKI D, AVITABILE P. Experimental issues related to frequency response function measurements for frequency-based substructuring[J]. Mechanical Systems and Signal Processing, 2010, 24(5): 1324-1337.

Frequencyresponsefunctionbasedsub-structuringsynthesismethodwithflexibleequivalenceofinterface’sDOFs

ZHANG Yong， HOU Zhichao, ZHAO Yongling

(State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084)

Frequency response function based sub-structuring (FBS) synthesis method play a significant role in analyzing complex systems. However, it fails sometimes to produce acceptable results due to the absence of rotational DOFs’ frequency response functions (FRFs). Here, a method of flexible equivalence of interface’s DOFs was proposed. An interface was divided into several sub-interfaces. Assuming all sub-interfaces were rigid, through the least squares coordinate transformation, 6 DOFs were taken to describe all motion features of a rigid sub-interface to realize the rigid equivalence of a sub-interface. All equivalent DOFs of all sub-interfaces were synthesized to form a flexible equivalence of the original interface. The relationship between the interface’s flexible equivalent DOFs and its original DOFs was used to transform a substructure’s original FRFs, the substructure’s transformed FRFs were applied in FBS method. Simulation results showed that the flexible equivalence of interface’s DOFs can significantly improve the synthesis accuracy of FRFs.

frequency response function sub-structuring (FBS) synthesis; interface’s DOFs; flexible equivalence

科技部(2014DFG71590)

2016-03-30 修改稿收到日期：2016-06-30

张勇 男,博士生，1985年生

侯之超 男,博士,教授，1966年生

TH113.1

： A

10.13465/j.cnki.jvs.2017.17.030