电动车动力传动系机电耦合扭转振动分析与控制
于 蓬, 王珮琪, 章 桐,3, 陈诗阳, 郭 荣
(1. 同济大学 新能源汽车工程中心,上海 201804; 2. 同济大学 汽车学院, 上海 201804; 3. 同济大学 中德学院,上海 201804)
电动车动力传动系机电耦合扭转振动分析与控制
于 蓬1,2, 王珮琪1,2, 章 桐1,2,3, 陈诗阳1,2, 郭 荣1,2
(1. 同济大学 新能源汽车工程中心,上海 201804; 2. 同济大学 汽车学院, 上海 201804; 3. 同济大学 中德学院,上海 201804)
对电动车动力传动系统的机电耦合扭转振动进行分析与控制。利用整车转鼓试验测得稳态工况下的电流信号,分析引发传动系统扭转振动的主要电流激励谐次;基于最大转矩电流比控制方法,结合传动系统机械振动模型,搭建综合考虑机械、电气相互影响的机电耦合模型,进行仿真分析;提出能够减小传动系统扭转振动幅值的电流谐波优化方法,阐述其原理并搭建其控制模块。控制前后的仿真结果表明,电流谐波优化方法可以有针对性的抑制电流的5倍、7倍谐波,减小6倍电流频率的转矩波动,降低传动系统在中高频固有频率处的振动幅值。
机电耦合;扭转振动;谐波电流;转矩波动
新能源汽车是目前国内外政府、企业以及高校研发的热点[1-2],其振动、噪声以及舒适性能在很大程度上决定用户的购买意愿,是研发过程中应予以关注的一个重点[3-4]。新能源汽车有别于传统车辆,其动力传动系统是主要区别之一,这使其振动和噪声性能具有自身的特点[5-6]。
电动车动力传动系统的振动噪声问题,按照现象划分,主要有喘振、颤振、高频短时撞击、半轴轰鸣、齿轮敲击、齿轮啸叫以及电机啸叫等[7];按照频率范围划分,大体可以划分为低频(0~10 Hz)、中频(10~100 Hz)、高频(100~2 000 Hz)三类振动。低频问题如电机启停(start-off)、突加/突减油门(tip in/out)造成的整车抖动[8],中频问题如减/差速器和行星齿轮的局部振动[9],高频问题如机电磁耦合振动等,均为国内外学者研究的典型问题[10]。中高频范围的扭转振动,鉴于其对传动系统振动噪声性能、零部件耐久性以及电机控制精度的影响,将作为本研究的侧重点。
国内外对于电动车传动系统扭转振动的分析与控制已有一定基础。文献[11]提出了电动车动力传动系统的机电耦合振动问题,建立传动系统模型,分析了同时考虑电气-机械因素对扭转振动的影响,但模型过于简化,有待深入;文献[12]将电磁刚度理论引入新能源车辆的研究中,进一步证明了综合考虑机电因素可以得到丰富的动力学现象的假设;文献[13]建立了详细的纯电动车动力传动系统模型并进行仿真研究,但在扭转振动的抑制方面未作涉及,工程指导意义有限。另外,目前有关电动车振动控制的案例,大都从被动优化的角度切入,如斜槽、齿槽配合、调整相位角[14-15]等,工程实现难度较大、成本高,未能较好的体现机电一体化系统的优势。
本文在以往研究的基础上,进一步建立综合考虑电机控制因素和传动系统机械因素的模型,提出用谐波电流优化方法减小电机输出转矩波动以及传动系统扭转振动的措施,并加以仿真效果验证,有效抑制电动车传动系统在中高频范围内、特定谐次电流波动作用下的扭转振动。所做研究为从主动控制的角度逐步解决电动车动力传动系统的扭转振动问题提供一定的理论支持。
1 电动车多工况电流试验
在电动车驱动系统中,由于检测精度、电流谐波、逆变器频率等因素的影响,往往产生电流畸变,畸变电流引发电磁力矩的波动,波动转矩将使传动系统产生受迫振动,影响系统性能。通过测量畸变电流,可以把握传动系统扭转振动的程度,为从供电角度降低传动系统的扭转振动奠定基础。
为获取某集中式电动车电驱动动力总成在真实工况下的电机输出电流,在转毂试验台上进行电驱动动力总成的振动测试试验,用电流示波器采集不同工况下的电流信号。测试现场布置、测试工况等可参见文献[16],该文已经对整车状态下的振动信号进行了详细的提取与分析,但是对于电流信号的分析不够,本文在此基础上,进一步分析电流谐波的主要成分,为后续有针对性的控制奠定基础。
在10 km/h~80 km/h稳速巡航条件下,每间隔10 km/h进行一次测量,记录振动信号。以车辆在10 km/h稳态工况下的电流信号为例进行说明,其时域频域曲线,如图1所示。
从时域曲线看,试验所测得电流峰值基本稳定在17 A,但实测工况下的电流产生了较大的畸变;进一步进行频域分析可以看到,试验电流的频域曲线展现出了更为丰富的频率峰点,主要的电流频率集中在45 Hz、88 Hz、225 Hz、264 Hz、315 Hz、484 Hz。峰值较大的频率点为45 Hz、225 Hz、315 Hz,分别对应电流基频的1倍、5倍、7倍,表明实际电流存在较大的5倍、7倍谐波,较小的频率点峰值的产生是因为在实际系统中,一方面由于直流偏移误差、相位误差以及增益误差的存在,会产生较高幅值的电流谐波,造成较大的转矩波动和电磁振动。另一方面实际中的定转子之间的静态和动态偏心等机械因素引起。
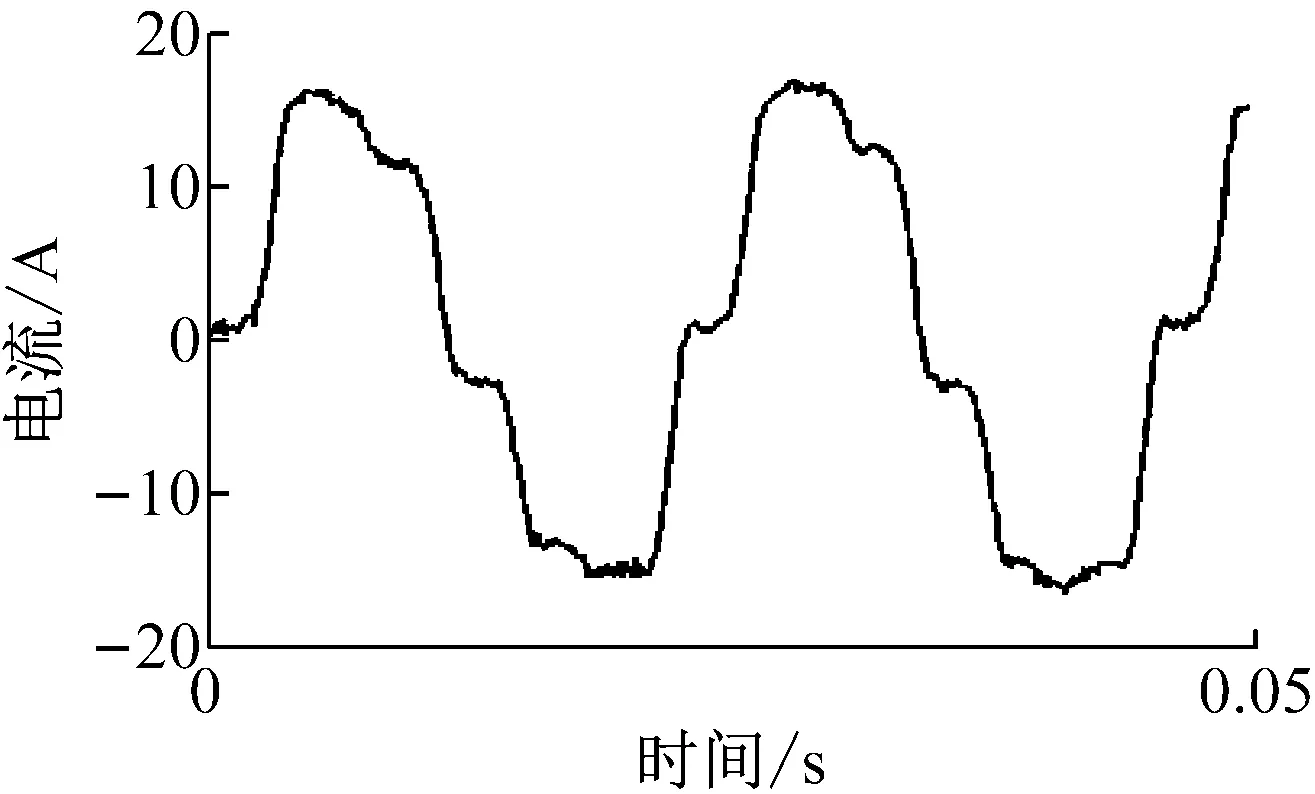
(a) 电流时域图
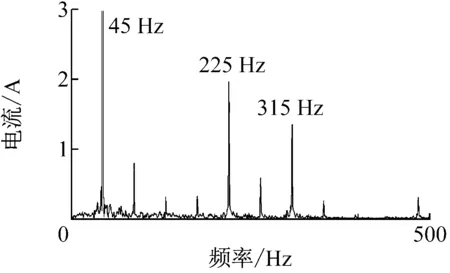
(b) 电流频域图
对车速20 km/h~80 km/h的工况,进行稳态试验,用示波器采集电流信号并进行频谱分析也得到了相同的规律,电动车在工作中存在较为明显的电流谐波,主要集中在电流的5倍频和7倍频处,谐波的幅值在1 A左右,这些谐波将引发较为明显的转矩波动,从而加剧电传动系统的扭转振动。所有稳态工况下的电流谐波幅值汇总于表1。值得注意的是,在某些工况下,电流的2倍频峰值也比较可观,这与车辆在试验工况下电机电流的检测精度以及谐波电流有关。电流检测时的增益失配、相位偏差以及3倍次的谐波电流,都将引发电流2倍频处的峰值,这在试验中是不可避免的,并不作为后续仿真关注的重点。
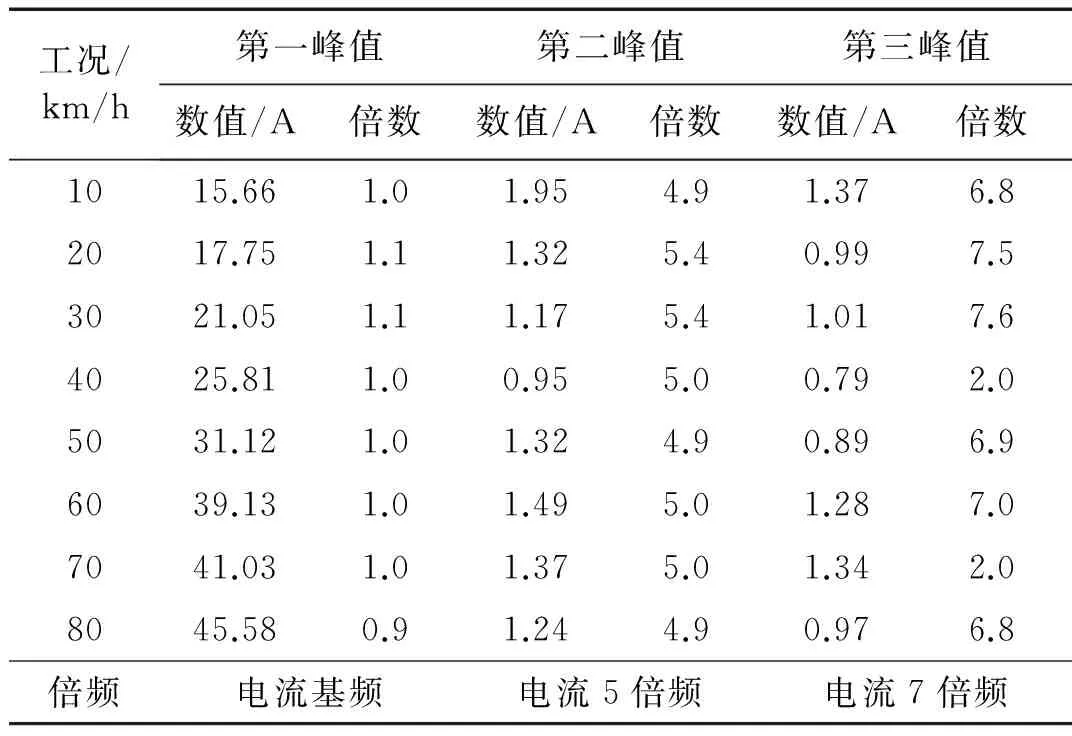
表1 各工况电流频域峰值汇总
2 机电耦合扭转振动仿真
2.1最大转矩电流比控制
永磁同步电机的电枢电流在经过Clark和Park变换后,电磁的转矩方程为
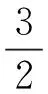
(1)
设γ为电枢电流与直轴的夹角,则有:
(2)
式中:np是电机极对数;Id、Iq是dq坐标系下的定子等效电流;Ld、Lq分别为电机直、交轴电感;φf为电机永磁磁链;Is是定子电流。
将式(2)代入式(1)得:
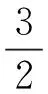
(3)
则单位电流下电磁转矩的表达式为
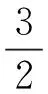
(4)
由于电流Is的幅值保持恒定,当∂f(γ)/∂γ=0时,单位电流下的电磁转矩取最大值,可以得到:
(5)
解得:
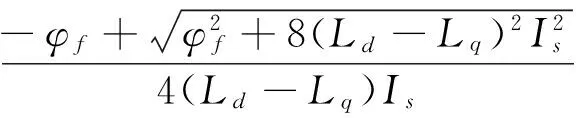
(6)
将式(6)代入到式(2)可得:
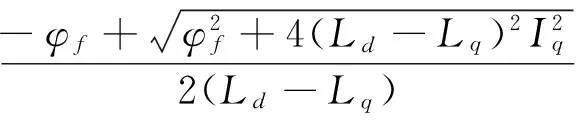
(7)
将式(7)代入式(3)可得:
(8)
2.2机械传动系统
对机械传动系统,采用模块化建模的方法,将整个动力传动系统分为电机转子、一级齿轮副、二级齿轮副、车轮、整车等效惯量和各个轴段进行模块化建模。在建模的过程中,充分考虑齿轮传动过程中的啮合刚度和可能存在的齿侧间隙。根据动力传动系统集中质量模型中各个部件以及部件之间的动力学方程,建立整个传动系统的SIMULINK仿真模型。机械系统动力方程的推导和仿真模型详见参考文献[13],不再赘述。
2.3机电耦合模型仿真
将最大转矩电流比控制下的电机模型和基于集中-弹性质量模型的机械系统相结合,得到考虑电机控制因素的机电耦合模型,如图2所示。
图3、图4为10 km/h工况下,机电耦合仿真的电流时域频图、转矩时频域图,为说明机电耦合模型和单纯考虑控制电机模型的不同,图中同时给出了不考虑机械传动系统的基于最大转矩电流比控制的电机输出结果。
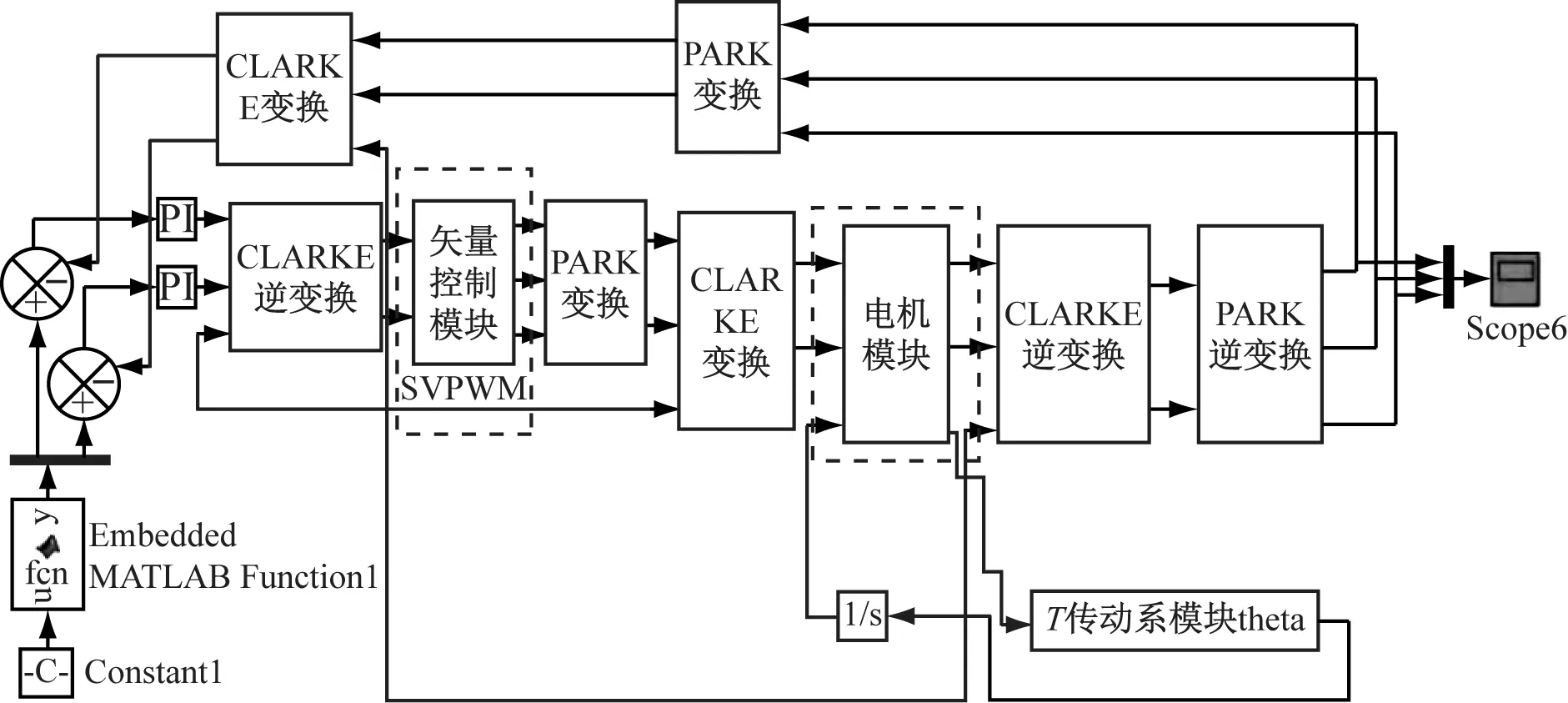
图2 机电耦合模型
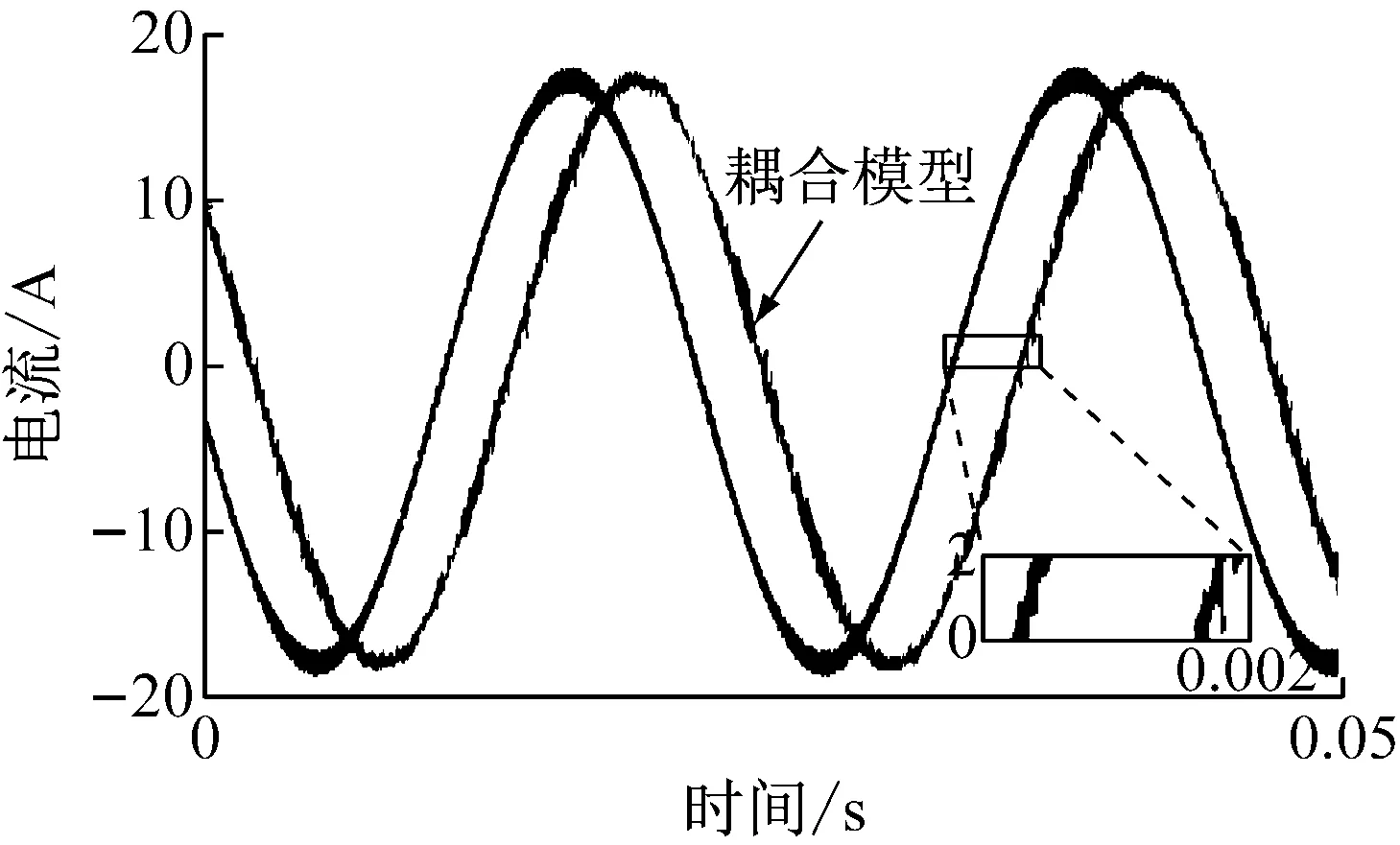
(a) 电流时域图
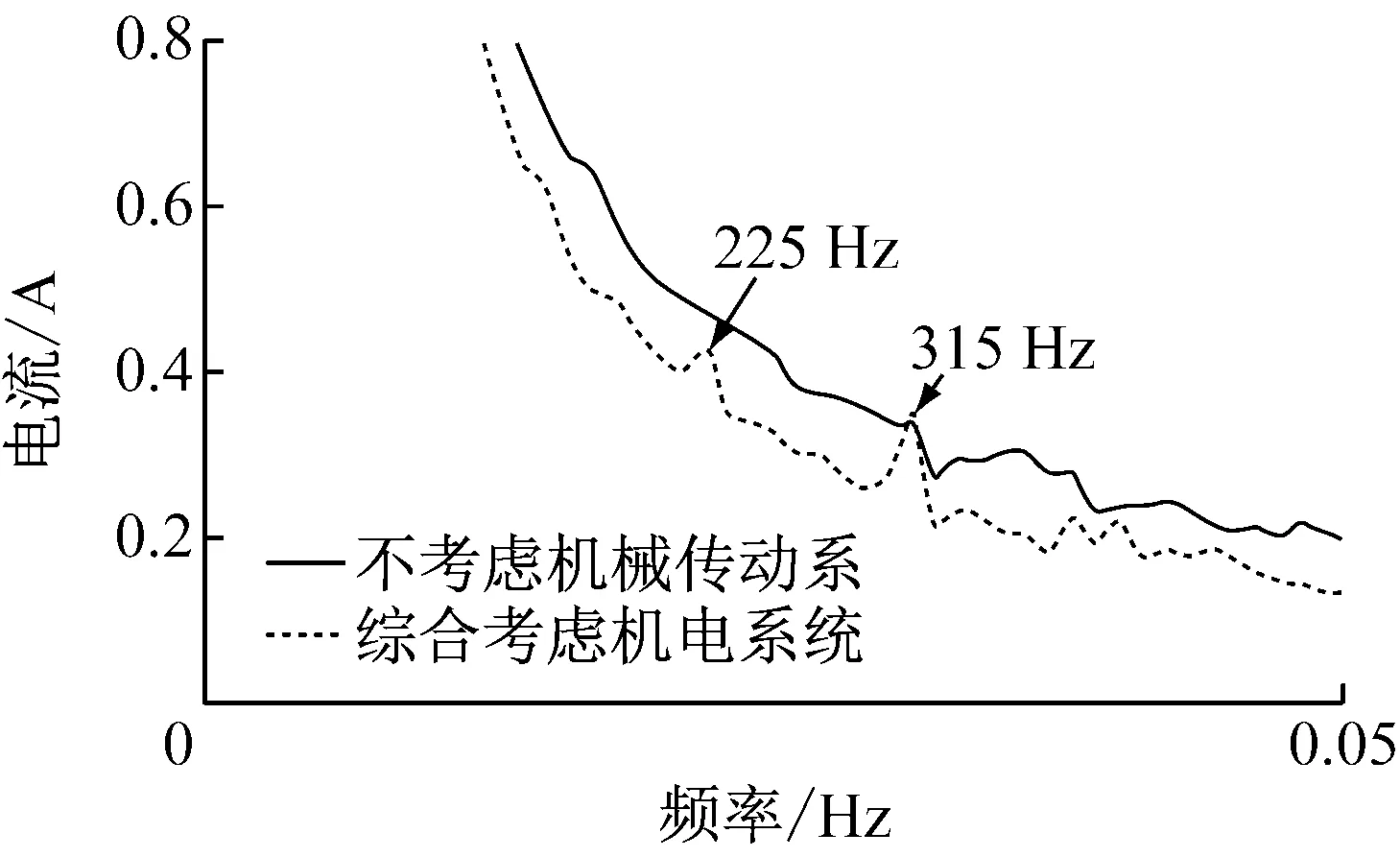
(b) 电流频域图
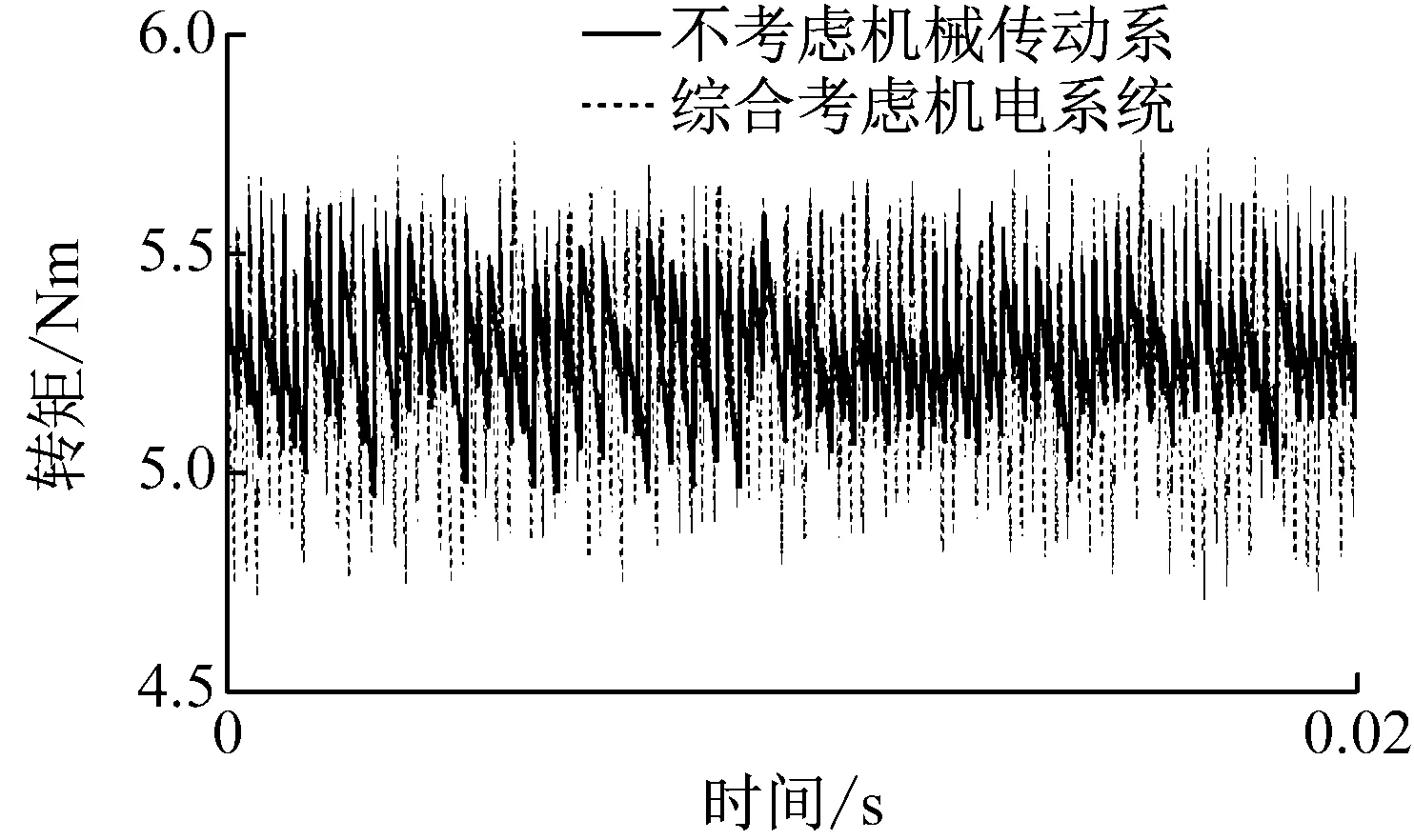
(a) 转矩时域图
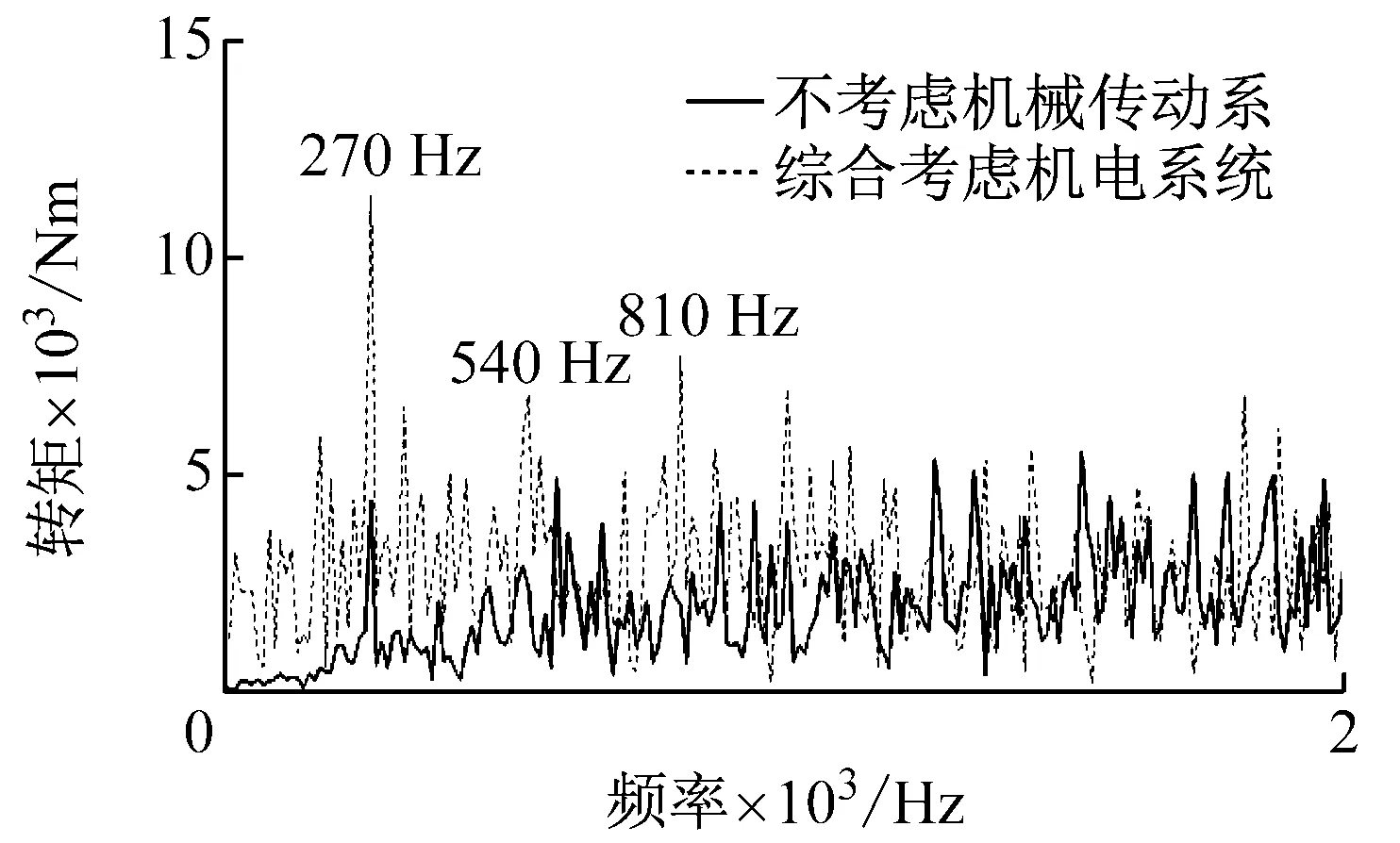
(b) 转矩频域图
对比图3(a)、(b)可以发现,在综合考虑了传动系统和最大转矩电流比控制策略后,电机输出电流波动范围由原来的1 A变为1.5 A,即电流波动更大;电流频谱分析时的平均幅值略微减小,但值得注意的是,电流频谱分析时在45 Hz、220 Hz、315 Hz附近出现了三个峰值。仿真工况N=675 r/min,此时转子基频f0=11.25 Hz,电流基频f=pf0=45 Hz。所以这些分别是电流频率的1倍频、5倍频、7倍频,这与试验中的结论一致。
对比图4(a)、(b)可以发现,在综合考虑了传动系统和最大转矩电流比控制策略后,电机输出转矩波动范围由原来的0.5 N·m变为0.8 N·m,即转矩波动更大;转矩频谱分析对比图显示,添加传动系统后,在2 000 Hz频率以下,转矩幅值增加,特别是270 Hz、540 Hz以及810 Hz处,有三个明显峰值,分别对应电流的6倍频、12倍频以及18倍频,这与以往分析中的结论一致[3-5,16]。
为验证上述描述为普遍情况,对车速为30 km/h的工况仿真结果进行分析对比。图5为30 km/h工况下,单独考虑控制策略以及综合考虑控制策略和传动系统时的电流频域、转矩频域图。
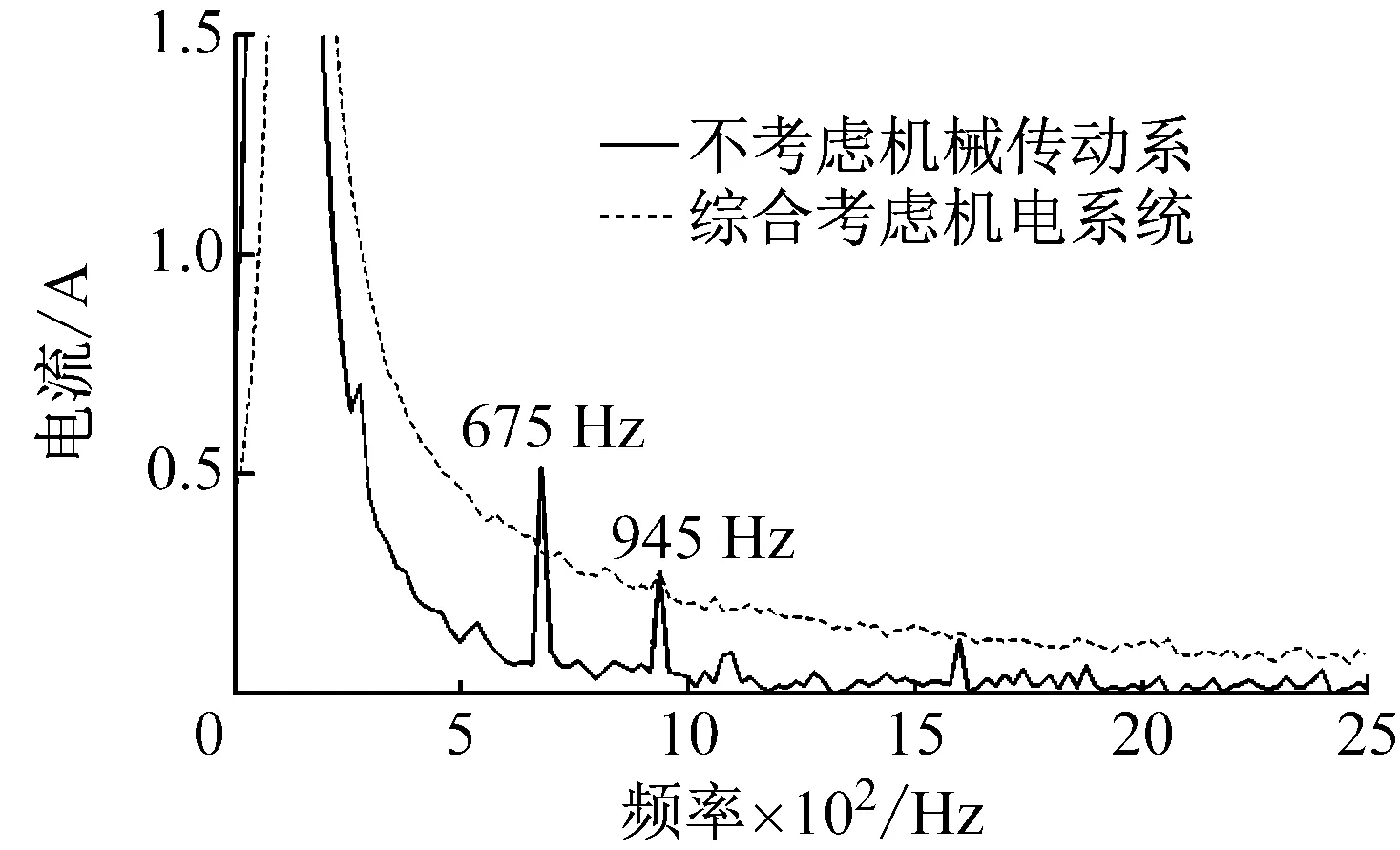
(a) 电流频域图
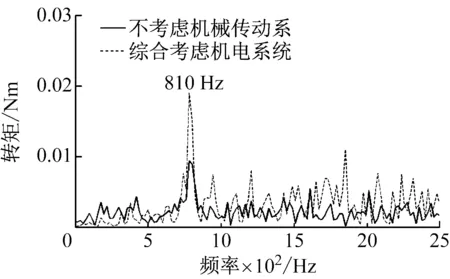
(b) 转矩频域图
从图5(a)、(b)可以看出,在添加传动系统后,最大转矩电流比控制策略下,电机输出电流波动,在频域上,添加传动系后的电流频谱曲线整体幅值降低,但在675 Hz、945Hz频率点处的幅值明显增加。此时仿真工况为N=2 024 r/min,转子基频f0=33.75 Hz,电流基频f=pf0=135 Hz。所以675 Hz和975 Hz分别是电流基频的5倍频、7倍频,而转矩的频谱分析结果中,也明显观测到810 Hz,也就是电流基频的6倍频处的峰值,与前述仿真和试验中的分析结果一致。
其余工况下的仿真结果类似,说明综合考虑控制策略和传动系统时,电流和转矩在时域上的波动值比单独考虑控制策略时要大;在频域上,综合考虑控制策略和传动系统时,电流和转矩将出现很多峰值,反映出更为丰富的动力学现象,更加符合工程实际。
3 电流谐波优化方法
3.1谐波优化理论
考虑电机定子的三相对称电流时,忽略定转子槽、线圈绕组形式等影响因素,则三相电流可以表达为如下形式:
(9)
式中:w为电流频率;t为时间;ik和φk分别为k阶电流谐波的幅值和相位。
对电机电流的谐波优化首先需要将电机的定子三相电流通过PARK变化转化为直交轴电流形式,公式如下:
(10)
(11)
式中:ia、ib、ic为三相电流;Id、Iq为直交轴电流,Tdq为转换矩阵。
将式(9)和(11)代入式(10)最终得到电机定子直交轴电流的表达形式为
(12)
(13)
(14)
式(13)和(14)中,d轴(直轴)的计算公式取正负号中的正号,q轴(交轴)对应负号。mod的取值取决于arctan中值的正负,若其值为正,则mod=0;若为负,mod=π。
经过推导可以发现,电机直交轴电流某阶次(6k次)谐波是由与其相邻阶次的三相电流谐波(6k±1次)组成的,如电机直交轴的第6次谐波是由电机三相电流的第5和第7次谐波组成。因此,如果要针对消除电机三相电流中的5次和7次谐波,最直接的方法是消除电机直交轴电流中的6次谐波。
3.2谐波优化方法的实现
通过式(7)、(8)可以看到,电机的输出转矩由其直交轴电流决定,因此通过优化电机定子电流的谐波,可以降低电机输出转矩的阶次波动。本文基于建立的最大转矩电流比控制策略进行谐波优化。通过反馈电机定子电流中目标消除的指定阶次电流谐波到经典控制环中进行谐波抵消,谐波优化的原理,如图6所示。
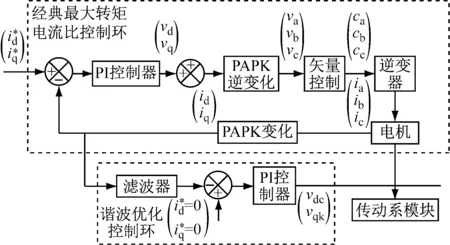
图6 谐波优化原理图
通过前面的仿真和试验结果分析,可以看到,转矩波动最大幅值谐波主要在6倍电流频率处,其原因在于电机直交轴电流的第6次谐波。根据谐波优化理论,消除该次谐波同样能达到衰减电机三相电流中的第5和第7次谐波的效果。具体的控制策略优化过程为:① 设计带通滤波器,选用需要的窗函数,针对要消除谐波的频率选择通带的范围和采样频率;② 电机输出三相电流经PARK变换后输入滤波器,获取直交轴电流的目标阶次谐波,径PI控制器变化为电压,输入到矢量控制的输入端进行反馈抵消。
4 扭转振动控制的效果
将谐波优化模块加载到前述机电耦合仿真模型中,得到如图7所示的具有谐波优化控制环的仿真平台。
以车速30 km/h的工况进行仿真,得到的结果与未优化的控制策略进行对比。观察图8,可以看到电机的三相电流谐波在控制策略优化后也得到了减小。A向电流原本在675 Hz以及945 Hz处的谐波幅值最大,该两处频率对应的是电机三相电流的第5和第7次谐波,优化后分别降低了38.2%和41.7%。
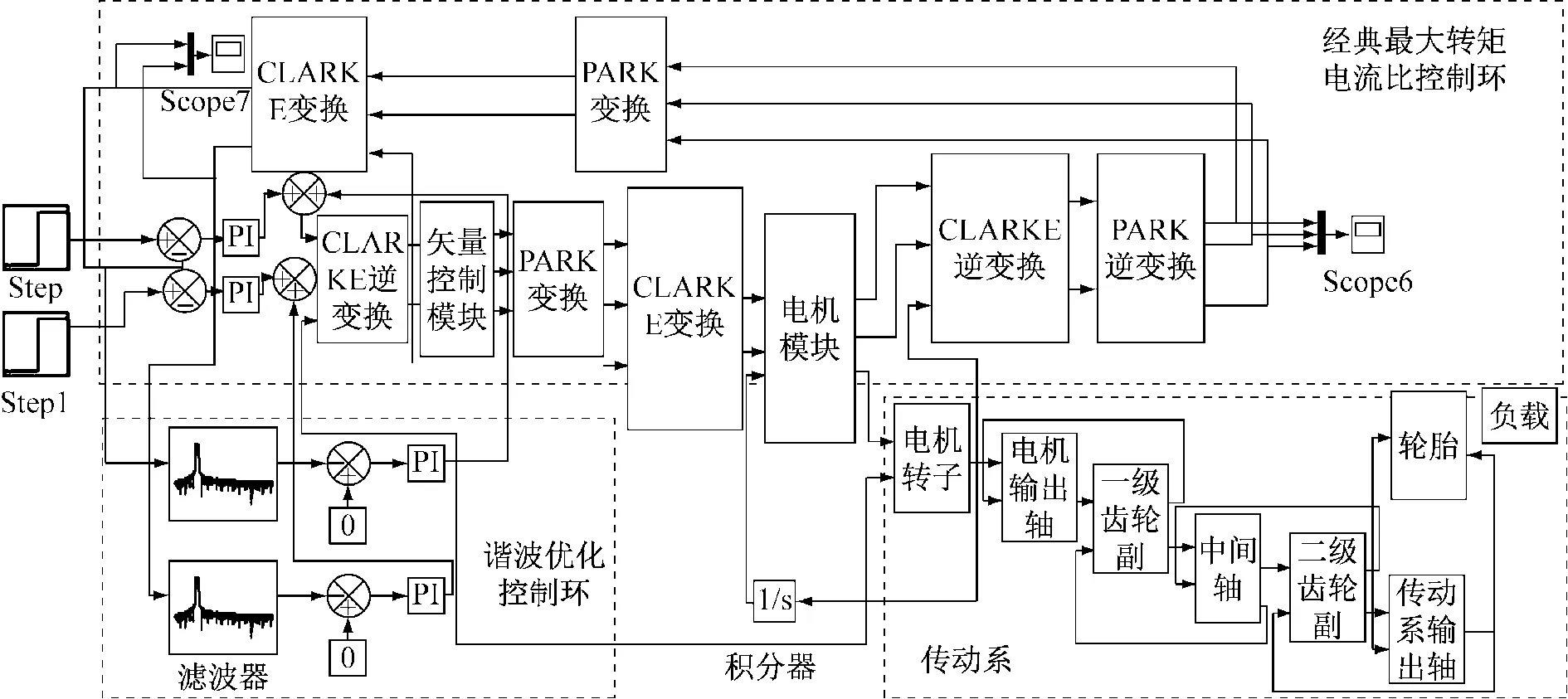
图7 基于谐波优化的机电耦合模型
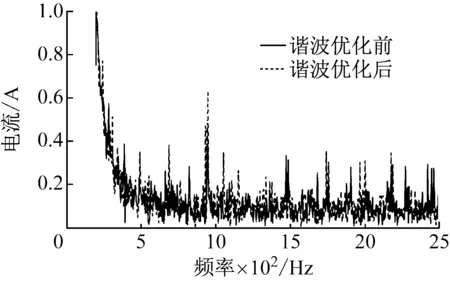
图8 定子A相电流谐波优化对比
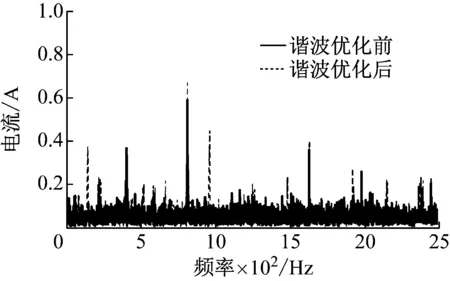
图9 电机输出转矩谐波优化对比
电机输出转矩波动的大小直接影响机械系统扭转振动的剧烈程度,从图9可以看到,电机转矩谐波在810 Hz处,也就是电流基频的6倍频处的峰值经谐波优化后得到了明显的衰减,从0.02 N·m降低为0.017 N·m,下降了15%。该谐波峰值的降低对传动系扭转振动的衰减将起到积极的作用。
减/差速器输出端的转矩、转速频域图如图10、图11所示。谐波优化前的仿真曲线与文献[13]的结果一致,630 Hz、2 000 Hz为传动系统由于减/差速器的存在而产生的局部模态频率,在这两个频率上,均体现出了机电耦合作用下的较为丰富的现象。而在加入谐波优化模块后,仿真结果显示,在这两个主要频率处的扭转振动峰值均有不同程度的减小,说明谐波优化方法在减小电流谐波和电机输出转矩波动的同时,也在一定程度上减小了传动系统扭转振动的峰值,体现了机电一体化控制的有效性。
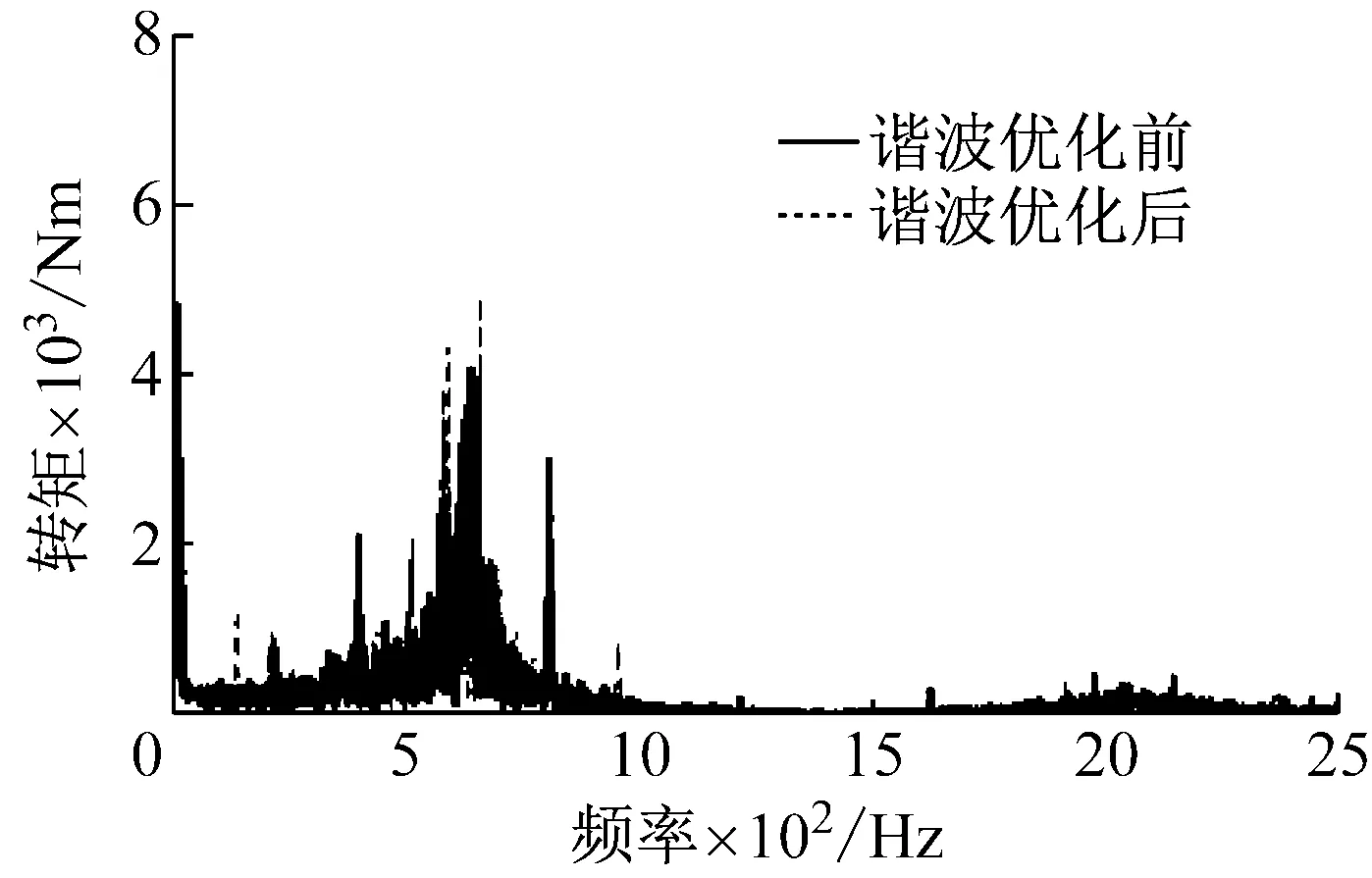
图10 减/差速器处输出转矩
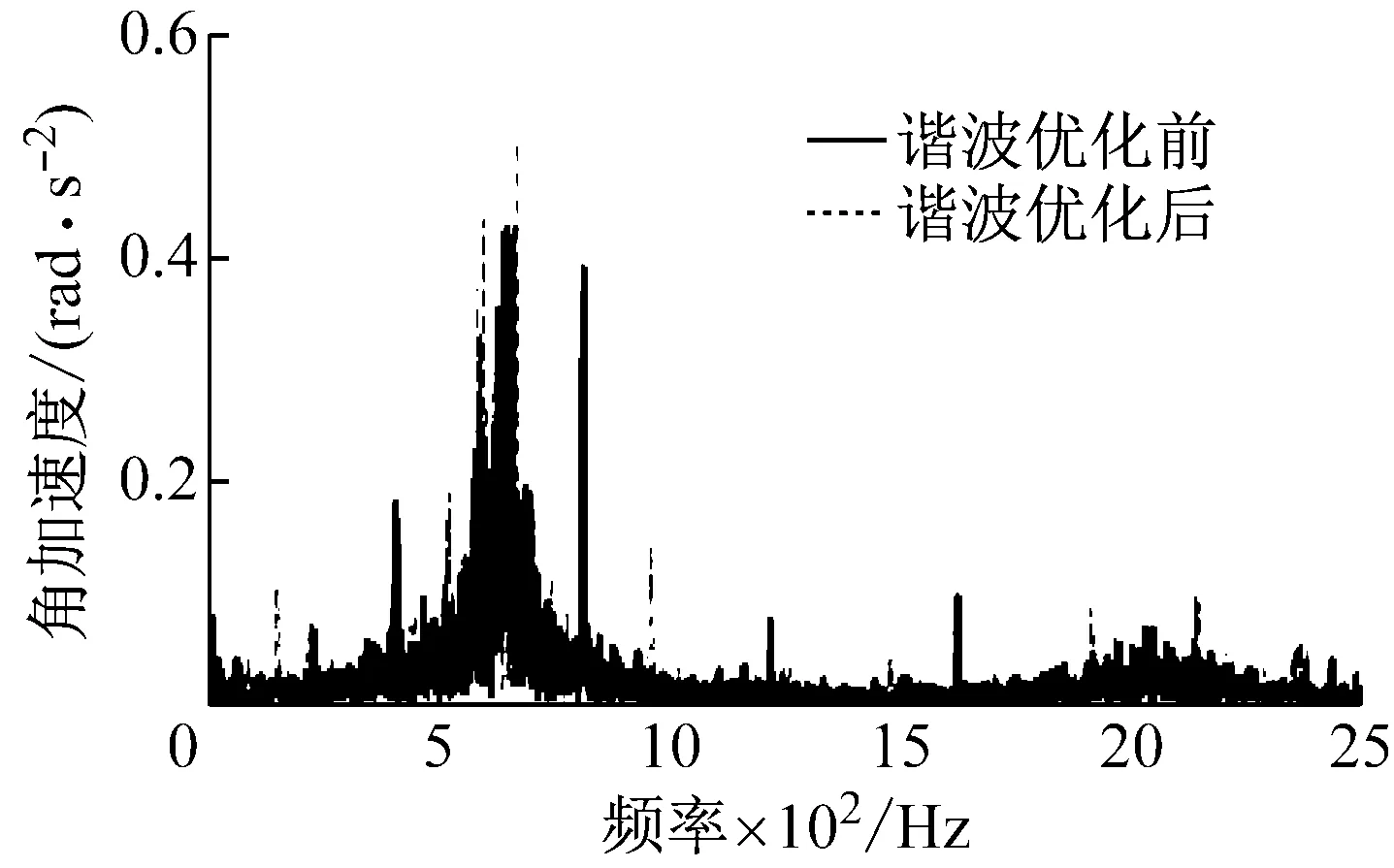
图11 减/差速器处输出角加速度
5 结 论
(1) 通过整车多工况下的电流测试试验,诊断出引发电动车动力传动系统中高频扭转振动的主要频率成分是电流输出基频的5倍频和7倍频。
(2) 综合基于最大转矩电流比控制的电机模型和基于集中-惯性质量的机械传动系统模型,搭建了能够反映典型电流谐次的机电耦合模型,并通过仿真得到典型倍次为6i(i=1,2,…)倍电流基频及其倍频的电机转矩波动,作为优化控制的目标。
(3) 提出谐波电流优化方法,搭建谐波电流优化模块,将其加载到机电耦合仿真平台上进行效果验证。仿真结果表明,所提方法能够有针对性的抑制5倍和7倍电流谐波,减小6倍电流基频的电机转矩波动,从而降低传动系统扭转振动的峰值。
所做研究针对某集中驱动式纯电动车进行,通过控制电机相关物理量改善了传动系统的扭转振动,体现了电动车传动系统机电一体化的特点。后续可以进一步优化传动系统的机械结构,将主动控制与被动优化相结合,进一步解决电动车传动系统的扭转振动问题。
[1] MIZUTANI R, TACHIBANA T, MORIMOTO M, et al. Electric drive technologies contributing to low-fuel-comsumption vehicles[J]. Ieee Transactions on Sensors & Micromachines, 2015, 135(9):884-891.
[2] CHO Y, BLOMMESTEIN K V. Investigating the adoption of electric vehicles using agent-based model[C]//2015 Proceedings of PICMET '15: Management of the Technology Age. 2015.
[3] 左曙光, 林福, 孙庆,等. 极槽配合和绕组层数对永磁同步电机振动的影响分析[J]. 振动与冲击, 2014,33(13): 130-134.
ZUO Shuguang, LIN Fu, SUN Qing, et al. Vibration of permanent magnet synchronous motor with different slot-pole combinations and winding layers[J]. Journal of Vibration and Shock, 2014,33(13): 130-134.
[4] 马琮淦, 左曙光, 孟姝,等. 考虑开槽和高次谐波的永磁同步电机解析模型[J]. 振动、测试与诊断, 2015, 35(2): 231-237.
MA Conggan, ZUO Shuguang, MENG Shu, et al. Analytical model of permanent magnet synchronous considering slotting and high harmonics[J]. Journal of Vibration, Measurement & Diagnosis, 2015, 35(2): 231-237.
[5] MA C, LIU Q, WANG D, et al. A novel black and white box method for diagnosis and reduction of abnormal noise of hub permanent magnet synchronous motors for electric vehicles[J]. IEEE Transactions on Industrial Electronics, 2015:1-1.
[6] 于蓬, 贺立钊, 章桐,等. 集中电机驱动车辆动力传动系统NVH性能研究现状与展望[J]. 机械设计, 2014,31(3):1-5.
YU Peng, HE Lizhao, ZHANG Tong, et al. NVH performance study of centralized motor driven vehicle power train[J]. Journal of Machine Design, 2014,31(3):1-5.
[7] 于蓬, 章桐, 郭荣. 车辆传动系扭转振动主动控制研究现状及趋势[J]. 机电一体化, 2014(6):3-10.
YU Peng, ZHANG Tong, GUO Rong. The current state and trends of automotive drive train torsional vibration active control[J]. Mechatronics,2014(6):3-10.
[8] ZHANG J W, LIU D, YU H. Low-frequency vibration responses of a single-mode power split HEV drive train[J]. Sae Technical Papers, 2015-01-1123.
[9] 于海生,张彤,马智涛,等.行星排式混合动力汽车传动系扭转振动分析[J].农业工程学报,2013(15):57-64.
YU Haisheng, ZHANG Tong, MA Zhitao, et al.Torsional vibration analysis of planetary hybrid electric vehicle driveline[J]. Transactions of the Chinese Society of Agricultural Engineering, 2013(15):57-64.
[10] ZHANG J, TANG X, YU H, et al. Multi-body dynamics and noise analysis for the torsional vibration of a power-split hybrid driveline[J]. Proceedings of the Institution of Mechanical Engineers Part K Journal of Multi-body Dynamics, 2014, 228(4):366-379.
[11] YU P, ZHANG T, LIU P. Mechanical and electrical coupling vibration characteristic analysis of power train system for electric driven vehicle[J]. Applied Mechanics and Materials, 2012, 224:385-388.
[12] YU P, ZHANG T, CHEN S, et al. Torsional vibration modeling of driveline system for EV low-frequency flutter[C]. SAE Technical Paper, 2015-01-2191.
[13] 于蓬,章桐,孙玲,等. 集中驱动式纯电动车动力传动系统扭转振动研究[J]. 振动与冲击, 2015, 34(10): 121-127.
YU Peng,ZHANG Tong,SUN Ling,et al. Powertrain torsional vibration study of central-driven pure EV[J]. Journal of Vibration and Shock,2015, 34(10): 121-127.
[14] SUN T, KIM Y H, CHO W J, et al. Effect of pole and slot combination on noise and vibration in permanent magnet synchronous motor[J]. IEEE Transactions on Magnetics, 2011, 47(5):1038-1041.
[15] TESSAROLO A, MEZZAROBBA M. On the computation of rotor losses through a set of harmonic finite element analyses in fractional-slot concentrated-coil permanent-magnet machines[C] //EUROCON-International Conference on Computer as a Tool, IEEE, 2011:1-4.
[16] 于蓬,王晓华,章桐,等. 集中式驱动纯电动车振动特性试验研究[J]. 振动与冲击,2015, 34(14): 38-44.
YU Peng, WANG Xiaohua, ZHANG Tong, et al. Experimental study on vibration characteristics of central driven pure electric vehicle[J]. Journal of Vibration and Shock, 2015, 34(14): 38-44.
Electro-mechanicalcoupledtorsionvibrationanalysisandcontrolofelectricvehicledrivelines
YU Peng1,2, WANG Peiqi1,2, ZHANG Tong1,2,3, CHEN Shiyang1,2, GUO Rong1,2
(1. New Clean Energy Automotive Engineering Center,Tongji University, Shanghai 201804, China;2. School of Automotive Studies, Tongji University,Shanghai 201804, China;3. Sino-German College of Applied Sciences, Tongji University, Shanghai 201804, China)
Electro-mechanical coupled torsion vibration of an electric vehicle driveline was analyzed and controlled. Firstly, current signals under the steady state condition were measured with the whole vehicle drum tests. The current’s main harmonic components exciting the driveline’s torsion vibration were analyzed. Secondly, based on the maximum torque to current ratio control method, combined with the mechanical vibration model of the driveline system, an electromechanical coupled model considering mechanical-electrical interactions was built, it was used to conduct simulation analysis. Finally, the optimization method for the current’s harmonic components was proposed to reduce the drive system’s torsion vibration amplitude, its principle was presented and its control module was constructed. Simulation results before and after the control showed that the current’s harmonic component optimization method can be used to suppress the 5th order current harmonic component and the 7th order one, reduce the torque ripple with 6 times of the current frequency, and reduce the driveline’s torsion vibration amplitudes at its middle and higher natural frequencies.
electro-mechanical coupled; torsion vibration; harmonic current; torque ripple
国家863计划项目2011AA11A265;国家自然科学基金(51205290);中央高校基本科研业务费专项资金项目(1700219118)
2016-03-14 修改稿收到日期:2016-05-30
于蓬 男,博士,1986年生
章桐 男,教授,博士生导师,1960年生, E-mail:tzhang@fcv-sh.com
U469.72
: A
10.13465/j.cnki.jvs.2017.17.002

