多元回归分析法在标准厂房基础沉降监测中的应用
王 丽
宿州学院环境与测绘工程学院,宿州 ,234000
多元回归分析法在标准厂房基础沉降监测中的应用
王 丽
宿州学院环境与测绘工程学院,宿州 ,234000
利用标准厂房沉降观测数据建立数学模型,对标准厂房基础沉降监测趋势作出预测,判断标准厂房安全状态。采用数理统计多元回归分析方法,确定影响标准厂房基础沉降的影响因子,分析影响因子对因变量影响程度大小,建立多元回归分析方程。对建立的多元回归分析方程通过假设检验思想进行模型检验,通过相关系数检验、F检验和T检验方法,检验模型是否有效。如果模型有效,便可以对标准厂房基础沉降趋势作出预测。分析结果可知,建立的多元回归分析模型相关系数为0.991,接近于1,相关性较好,通过相关性检验。F检验的统计值概率P小于显著水平0.05,说明影响因子对多元回归方程整体影响显著。T检验统计值t大于临界值,说明每个沉降影响因子对因变量的影响显著。通过以上模型检验,说明建立的多元线性回归方程是有效的,可以预测标准厂房基础沉降趋势,判断标准厂房安全状况。
多元回归分析方法;相关性检验;F检验;T检验;沉降率
随着我国城市化进程不断加快,高层建筑物越来越多,这些高层建筑物随着荷载的加大,可能会带来安全隐患。为了保证建筑物安全,需要定期对建筑物进行沉降观测,分析建筑物的安全状态,确保建筑物的安全性。
现对某厂房进行定期沉降监测,分析厂房沉降状况。运用数理统计回归分析理论,建立回归分析模型,寻找标准厂房沉降量和沉降因子之间的函数关系。如果考虑多种沉降因素,将多个沉降因子作为自变量,建立多元回归分析模型,采用建立的多元回归分析模型,预测标准厂房的沉降量变化情况,以判断标准厂房的安全状况。
1 多元回归分析预测模型
1.1 多元回归分析预测模型的建立
回归分析理论是建立因变量和自变量之间的函数关系,如果因变量和自变量之间呈现近似线性函数关系,便可建立多元线性回归分析模型,预测和分析建筑物的安全状况[1]。假设多元回归分析模型影响因素为x1,x2,…,xm,预测对象为y,建立经典多元线性回归分析模型为:
y=b0+b1x1+b2x2+…+bmxm+ε
(1)
其中,ε~N0,σ2是偶然误差项,b0,b1,b2,…,bm是待估计参数。
如果有n个因变量y,即多元线性回归模型可写成:
Y=XB+ε
(2)
其中:Y=(y1,y2,…,yn)T,
B=b0,b1,b2,…,bmT
B=XTX-1XTY
(3)
解出带估计参数b0,b1,b2,…,bm,从而建立多元线性回归方程,但多元回归模型还要进行模型检验以及相关系数R检验、显著性F检验和T检验。
1.2 多元回归分析模型检验
建立了因变量Y与自变量X之间的线性方程后,还需对所建立的模型进行相关系数R检验、显著性F检验和T检验[2-5]。
1.2.1 相关系数R检验
相关系数R检验是判断自变量X和因变量Y之间的线性相关程度,计算公式如下:
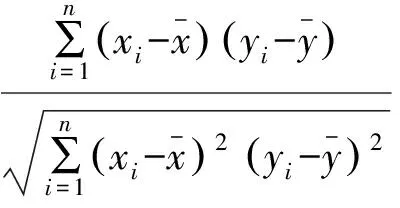
(4)
相关系数r越接近于1,说明因变量Y与自变量X之间线性相关性越好。但需要通过相关性检验:
(1)计算r;
(2)判断r值和拟定显著水平α的临界值rα的大小;
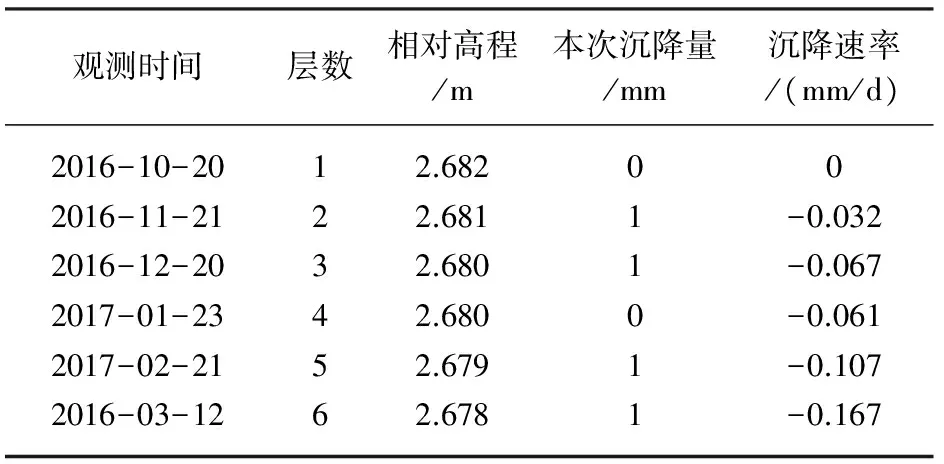
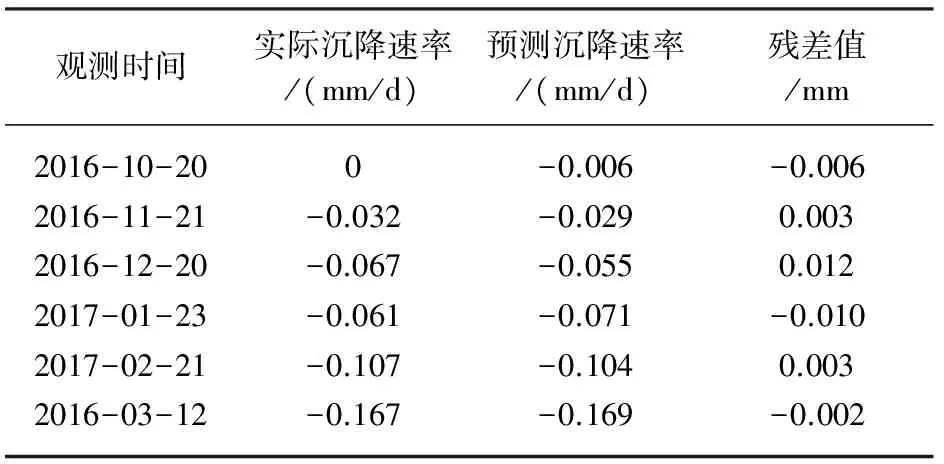
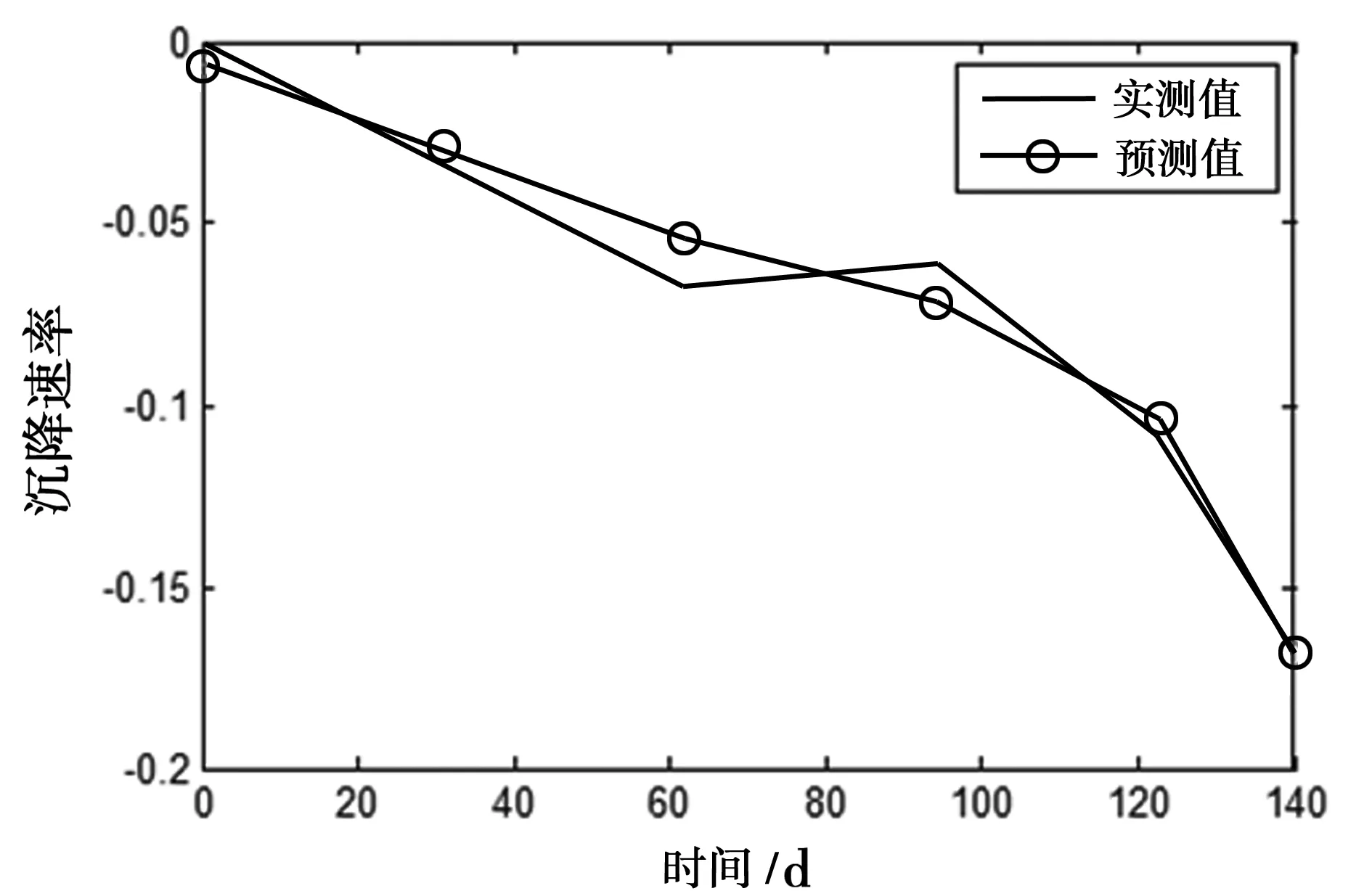
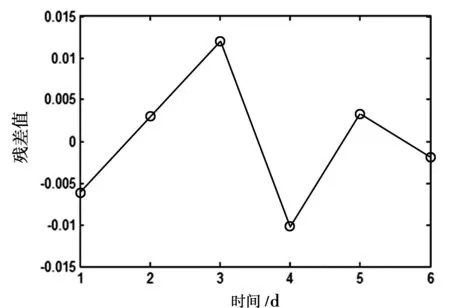
(3)若r>rα,说明因变量Y与自变量X呈现显著线性相关;若r 1.2.2 显著性F检验 F检验是判断自变量X整体对因变量Y的影响程度,公式如下: (5) 根据F检验表,查得显著水平α的临界值Fα,判断大小关系。若F 1.2.3T检验 T检验是判断自变量X中每个影响因子对因变量Y的影响显著性程度,T统计量计算公式如下: (6) 其中,cii为矩阵XTX-1主对角线上的第i元素。 根据T检验表,查得显著水平α的临界值tα,判断统计量t和临界值tα大小关系。若t>tα,则拒绝原假设,说明自变量X每个因子对因变量Y影响具有显著性;否则,说明自变量影响因子对因变量Y影响不显著,将其剔除。 当建立的多元回归方程通过以上检验,说明所建立的预测模型有效,可以用于对建筑物未来趋势作出预测。 某工程标准厂房中5#厂房于2016年10月21日开始进行设点观测,至2017年3月31日,总共进行6期观测,共设有12个沉降监测点,具体布置如图1所示。 图1 沉降监测点点位布置图 现选取M1号沉降监测点观测数据进行分析,并利用多元回归分析方法对其进行建模分析预测。观测数据如表1。 表1 M1号点沉降监测数据 2.1 多元回归模型的建立 引起5#厂房沉降的原因很多,根据表1,影响5#厂房沉降的沉降因子为观测时间和楼层增加的层数。 现将观测时间和楼层增加的层数作为影响因子自变量,将沉降速率作为因变量,建立M1号沉降监测点沉降速率与观测时间和层数之间的回归模型,并进行预测,为建筑物安全提供相关信息。 设观测时间为自变量x1,楼层层数为自变量x2,沉降速率为因变量y,采用Matlab软件编程建立二元线性归回归方程,得到回归方程为y=0.118+0.003x1-0.124x2。 2.2 多元回归模型检验 通过计算,得到沉降速率与观测时间和楼层层数之间的线性归回方程为y=0.118+0.003x1-0.124x2,现对模型进行相关性R检验、显著性F检验和T检验。 2.2.1 相关性R检验 运用Matlab软件计算,得到复相关系数R2为0.982,说明建立的二元线性回归模型线性相关性程度较好。下面通过相关性检验开始验证。 取显著水平α=0.05,查相关系数r临界表得rα=r0.05(4)=0.811,所以r=0.991>rα,说明自变量和因变量线性关系显著,通过了相关系数检验。 2.2.2 显著性F检验 计算得到F统计量的值的概率P为 0.002,小于显著水平α=0.05,所以拒绝原假设H0,认为建立的二元线性回归模型有意义,两个自变量对因变量沉降速率整体影响效果显著。 2.2.3T检验 计算得到与观测时间参数对应的t统计量为t1=3.105,楼层增加的层数参数对应的t统计量为t2=-4.088。取显著水平α=0.05,查t分布表,得到tα/2n-k=t0.0256-2 =2.776,与两个自变量所对应参数t统计量的绝对值相比,所得到的参数对应的t统计量的绝对值都大于临界值t0.0254 =2.776,所以两个自变量观测时间和楼层层数对因变量沉降速率的影响全呈显著性。 2.3 模型预测与精度分析 根据建立的多元回归模型方程,预测出6次沉降观测的沉降速率,和实际沉降速率值对比,得到的残差值如表2[6-7]。 表2 残差值表 根据预测值和实际观测值,绘制出预测沉降速率和实际观测沉降速率对比图(图2)和残差值图(图3)。 图2 实测值和预测值对比图 从残差值和预测值与实际观测值对比曲线图可以看出,监测点的预测残差值都小于0.01 mm,6期观测值残差值中误差为0.007,说明建立的模型精度较高[8-9]。 图3 残差值图 以上针对建筑物基础沉降速率与时间以及增加的荷载关系进行了分析,利用统计学中多元回归分析理论,建立了观测时间和增加楼层层数与沉降速率之间的回归方程,通过模型检验,说明建立的模型是有效的,预测精度较高。但文中只引入了观测时间和楼层层数两个沉降影响因子,由于引起建筑物基础沉降的原因很复杂,所以还可以引入更多的影响因子,通过建立回归模型对建筑物基础沉降状况进行分析,这有待于今后进一步研究。 [1]岳建平,田林亚.变形监测技术与应用[M].北京:国防工业出版社,2015 [2]熊俊楠,王泽根,徐忠印.高层建筑物变形监测数据处理方法研究及工程应用[J].测绘科学,2010,35(4) :69-71 [3]钱思众,樊育豪.高层建筑物地基沉降监测与分析[J].西安科技大学学报,2014,34(3):284-289 [4]刘兴亮,吴捷.高层建筑沉降监测数据处理分析[J].地矿测绘,2013,29(4):19-21 [5]丁宁,孙英君,崔健.高层建筑物变形监测数据处理与分析[J].测绘科学,2011,36(5):93-102 [6]陈小荣,雷劲松,卢学松.高层建筑沉降观测数据处理与分析新方法[J].四川建筑科学研究,2009,35(3):119-124 [7]郑丽.高层建筑沉降监测数据处理方法研究[J].佳木斯大学学报,2015,33(4):540-541 [8]王涛,袁曼飞.高层建筑物基准点稳定性及沉降监测数据分析[J].测绘与空间地理信息,2015,38(3):7-9 [9]袁伟韬,昆施,李振.高层建筑沉降观测水准基点稳定性分析[J].河南科学,2014,32(7): 1263-1265 (责任编辑:汪材印) P258 :A :1673-2006(2017)07-0114-03 10.3969/j.issn.1673-2006.2017.07.030 2017-04-19 宿州学院横向项目(2016hx007);宿州学院重点科研项目(2016yzd01)。 王丽(1987-),女,安徽安庆人,助教,硕士,研究方面:摄影测量与遥感、变形监测与数据处理。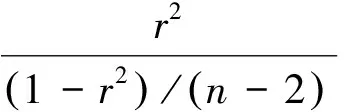

2 工程案例分析

3 结 语
——与非适应性回归分析的比较

