基于EFG法散热结构的最优拓扑构型设计研究

张丽娜，唐芳，刘吉普，陈优

基于EFG法散热结构的最优拓扑构型设计研究

张丽娜1，唐芳2，刘吉普1，陈优1

（1.湖南应用技术学院机电工程学院，湖南常德415100；2.湖南理工职业技术学院风能工程学院，湖南湘潭411105）

基于EFG法，提出了一种散热结构的拓扑优化设计方法。基于该方法，通过编程，进行了散热结构的最优拓扑构型设计。结果表明，该方法可以应用于散热结构的最优拓扑构型设计，并为工程散热结构的优化设计提供理论指导。

EFG法；散热结构；拓扑优化；变密度法

功率电子器件、发动机等产品的散热特性对其工作性能有重要影响，如计算机芯片的有效冷却已成为影响个人计算机性能进一步提高的瓶颈问题。传统散热结构的传热设计一般是假定特定结构，通过传热计算来进行，然而不同拓扑结构形式散热器的传热效果显然不同，如何寻找最佳传热拓扑结构，已成为工程传热结构优化设计的关键技术问题。

近年来，国内外部分学者提出利用结构拓扑优化方法，对传热结构的最佳拓扑进行设计。当前，传热结构拓扑优化研究主要基于有限元法进行。然而，由于有限元法采用基于单元的插值方法，温度场及拓扑优化中的单元相对密度场的连续性低，导致拓扑优化过程中常出现如棋盘格和网格依赖性等数值不稳定现象[1-2]，不利于工程应用。

无网格Galerkin（Element-Free Galerkin，EFG）法作为一种新型数值分析方法，具有计算精度高、收敛快和稳定性好等[3]优点，在结构大变形[4-5]、动态裂纹扩展[6-7]和结构优化[8]等众多计算力学领域得到了广泛应用。与有限元相比，EFG法采用基于离散点的逼近方法，可构造出高阶场函数，并且所得计算结果光滑连续，无需进行光滑化处理[9]。因此，本文将EFG法应用于传热分析，开展基于EFG法的传热结构拓扑优化研究，有望解决有限元法在传热结构优化中存在的问题，并对工程中散热结构的优化设计具有重要指导意义。

1 EFG离散模型

EFG法利用移动最小二乘法构造位移逼近函数，在二维热传导问题中，其温度场Th（x）的逼近函数为：

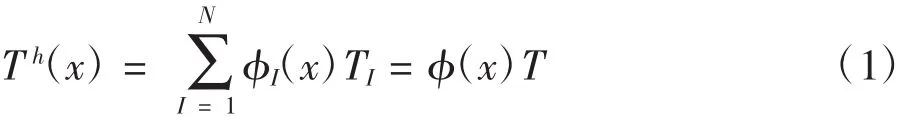
式中φ（x）为形函数。若采用罚函数法来处理本质边界条件，对于固体热传导问题，则EFG法的离散形式可表述为：

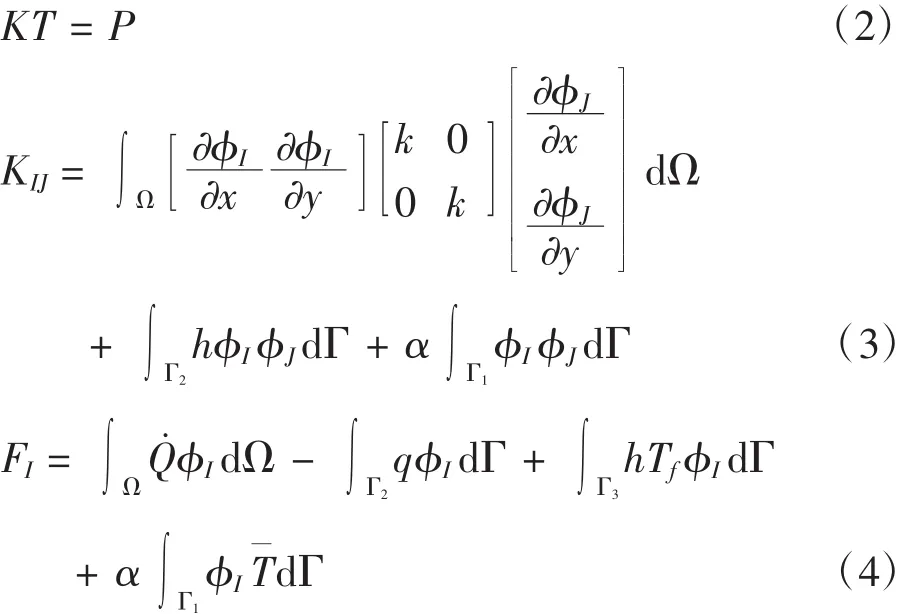
式中，K为总体温度刚度矩阵，由节点对温度刚度矩阵KIJ组装而成；T为节点温度参数向量；P为总体热载荷向量，由节点热载荷向量FI组装而成；α为罚因子。

式（3）与式（4）中均含有积分项，由于EFG法中积分项的被积函数并非简单的多项式函数，因此需要利用高斯积分进行计算。本文基于有限元背景积分网格，采用高斯积分进行计算。

2 拓扑优化模型

基于EFG法热传导问题的拓扑优化数学模型可表述为：

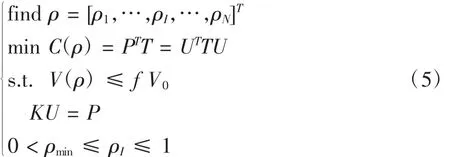
式中，ρ为设计变量矢量；C为结构的散热弱度；V（ρ）为优化后的结构总体积；V0为初始实体材料状态的结构总体积；f为材料的最大体积保留率；为避免优化过程中刚度矩阵的奇异，引入密度下限值ρmin，一般取0.001.

3 最优拓扑构型设计

算例：如图1所示，平板结构的长宽均为20 m，厚度为1 m，平板材料的热导率为10 w/cm·℃.平板的热载荷及边界条件如图1所示。

图1 中心热源平板模型及边界条件

本文采用规则排布的节点进行离散，得到图2所示的节点布置方案，节点总数为441.为了计算离散格式中的积分项，需要采用背景积分网格，本文采用与离散节点相重合的有限元背景积分网格，网格总数为400.

需注意的是，采用EFG法进行该结构的传热分析时，只需要一系列的离散点来构造温度场的逼近函数，而无需有限元背景网格（仅用于计算离散格式中的积分项，与温度场逼近函数无关），这是EFG等无网格方法与有限元法的本质区别。

利用EFG散热结构拓扑优化程序，对该模型进行求解，得到了最优拓扑布局，如图3所示。由图6可知，在结构体积满足一定约束的条件下，为保证最佳的散热效果，结构的材料均布置在平板中心点与四个顶点的连线上。

图4为原始平板结构的温度分布云图。由图4可知，在平板中心点与四个顶点的连线上，温度变化最大，即温度梯度最大，因此沿中心点与四个顶点的连线方向，散热效率最高。这与本文方法所得到的最优拓扑构型一致。

图2 初始节点排布

图3 最优拓扑构型

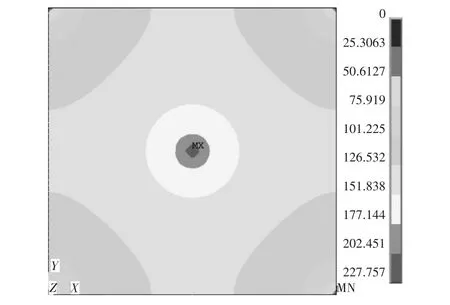
图4 原始结构温度分布云图

4 结论

本文提出了一种基于EFG法的散热结构拓扑优化设计方法。本文基于该方法编写了计算程序，进行了散热结构的最优拓扑构型设计。结果表明了本文方法可以应用于散热结构的最优拓扑构型设计，并为工程散热结构的优化设计提供理论指导。

[1]BENDSOE M P，SIGMUND O.Topology：Optimization：Theory，methods，and applications[M].New York：Springer，2003.

[2]SIGMUND O，PETERSSON J.Numerical instabilities intopology optimization：A survey on procedures dealingwith checkerboard，mesh-dependencies and localminima[J].Structural Optimization，1998（16）：68-75.

[3]Belytschko T，Lu Y Y，Gu L.Element-free Galerkin methods [J].International journal for numerical methods in engineering，1994，37（2）：229-256.

[4]Alfaro I，Yvonnet J，Cueto E，et al.Meshless methods with application to metal forming[J].Computer methods in applied mechanics and engineering，2006，195（48）：6661-6675.

[5]张希，姚振汉.无网格彼得洛夫伽辽金法在大变形问题中的应用[J].工程力学，2006，23（Sup.I）：16-20.

[6]Belytschko T，Krongauz Y，Fleming M，et al.Smoothing and accelerated computations in the element free Galerkin method [J].Journal of Computational and Applied Mathematics，1996，74（1）：111-126.

[7]蔡永昌，朱合华.裂纹扩展过程模拟的无网格MSLS方法[J].工程力学，2010，27（7）：21-26.

[8]龚曙光，曾维栋，张建平.Reissner-Mindlin板壳无网格法的闭锁与灵敏度分析及优化的研究[J].工程力学，2011，28（4）：42-48.

[9]张雄，宋康祖，陆明万.无网格法研究进展及其应用[J].计算力学学报，2003，20（6）：730-742.

Study on Topology Design of Heat Radiation Structure Based on EFG Method

ZHANG Li-na1，TANG Fang2，LIU Ji-pu1，CHEN You1
（1.School of Electrical and Mechanical Engineering，Hunan Applied Technology University，Changde Hunan 415100，China；2.School of Wind Engineering，Hunan Vocational Institue of Technology，Xiangtan Hunan 411105，China）

In this paper，a kind of topology optimization design method for heat radiation structure based on EFG method was established.According to the method，topology design of heat radiation structure was accomplished by using the EFG program.The result shows that the method can apply to topology design of heat radiation structure，and it is provided the guidance for optimization design of heat radiation structure.

EFG method；heat transfer body；topology optimization；SIMD

TH123

A

1672-545X（2017）07-0018-02

2017-04-05

湖南省教育厅科学研究一般项目（16C1173、16C0745）

张丽娜（1987－），女，河南鹤壁人，硕士，主要从事过程装备仿真及优化和节能与环保等研究；唐芳（1989－），女，湖南永州人，硕士，主要从事数值传热学及太阳能光热利用技术研究。