基于振动信号能量熵的轴承故障诊断

任玉卿 王海瑞 齐 磊 李荣远

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

基于振动信号能量熵的轴承故障诊断

任玉卿 王海瑞 齐 磊 李荣远

(昆明理工大学信息工程与自动化学院 云南 昆明 650500)

轴承大量存在于机械设备当中，轴承的故障也是各种机械故障的主要原因。对轴承故障及时和准确的判断，可以有效地预防由轴承故障引起的事故，减少损失。基于此提出一种基于振动信号能量熵的轴承故障诊断的方法。轴承在不同的工作状态下，轴承振动信号的能量熵不同，也就是能量分布也是不同的，可以通过能量分布的不同判断轴承的状态。首先对轴承的振动信号进行总体平均经验模态分解EEMD(Ensemble Empirical Mode Decomposition)，获得若干个本征模函数IMF(Intrinsic Mode Function)，然后计算本征模函数能量特征，将能量特征作为输入，可以建立相关向量机判断轴承的状态。通过实验验证，基于振动信号能量熵的故障诊断方法可以有效地应用于轴承的故障诊断。

总体平均经验模态分解(EEMD) 能量熵 相关向量机(RVM) 故障诊断

0 引 言

轴承大量存在于机械设备当中，尤其是旋转机械设备，其故障也是很多机械故障的主要原因。对轴承故障进行准确的诊断对机械设备的高效运行与维护有很大的帮助[1]。

机械设备故障诊断就是对含有故障信息的信号进行处理和分析，从信号中提取出和故障有关的特征参数，利用这些特征参数可以对机械设备进行故障诊断。故障诊断主要有两个方面的问题需要解决，一是信号特征参数的提取；二是对信号特征进行分类识别。

轴承的振动信号属于非平稳信号。在对非平稳信号的研究中，Huang等首先提出了经验模式分解EMD(Empirical Mode Decomposition)方法[2]。但EMD存在的模态混叠问题，在实际应用当中容易出现分解误差，因此Huang提出了总体平均经验模式分解EEMD[3-4]方法，该方法通过对原始信号加入白噪声分量，使不同区域信号保持连续性，解决了EMD的模态混叠问题。

总体平均经验模态分解在经验模态分解方法的基础上进行改进的一种自适应的新型信号处理方法。EEMD非常适合于非线性、非平稳信号，并且抗模态混叠能力相比EMD有很大改进。

支持向量机(SVM)在故障诊断和故障识别方面有很广泛的应用，其对于非线性信号具有很好的识别能力。但是支持向量机在实际应用当中存在一些不足，支持向量机分类器对参数有一定的要求，其核函数需要满足Mercer条件，解的相关向量较多，导致支持向量机分类器计算复杂度相对较大[5]。相关向量机是一种与支持向量机极其相似的稀疏概率方法，与支持向量机相比不存在以上的缺点。理论上相关向量机的泛化能力好于支持向量机，对于小样本问题的处理更加具有优势，对于实际工程问题处理更加适合[6]。相关向量机在保持较高的检测精度的同时，相对支持向量机模型解的稀疏性更加高，故障检测速度更加快[7-8]。

为此，使用EEMD方法与RVM方法，提出了一种基于振动信号能量熵的轴承故障诊断方法。

1 基本原理

1.1 EEMD的基本原理

EEMD方法是为了提高抗模态混叠的能力在EMD方法的基础上进行改进形成的。通过对原始信号加入白噪声分量，使不同区域信号保持连续性，减小模态混叠的程度[9]。其分解步骤和原理如下:

(1) 在原始信号x(t)中多次加入高斯白噪声ni(t)(白噪声均值为零，标准差为常数一般为原始信号标准差的0.1至0.4倍)即:

xi(t)=x(t)+ni(t)

(1)

式中:xi(t)为原始信号加入高斯白噪声ni(t)后的信号。信号EEMD模态混叠消弱的效果受到加入高斯白噪声的大小直接影响。

(2) 对xi(t)进行EMD分解，分解可以获得若干个IMF分量bij(t)，以及一个余项ri(t)。其中bij(t)表示对xi(t)进行EMD分解后得到的第j个IMF。

(3) 将步骤(1)和步骤(2)重复N次。由于高斯白噪声的统计均值为零，对IMF进行总体平均运算，可以消除高斯白噪声对计算结果的影响。最终可以获得EEMD分解后的IMF。

(2)

式中，bj(t)表示对IMF进行总体平均运算，获得的第j个IMF分量。当N越大，由加入白噪声造成的误差越小。此时EEMD分解的结果为:

(3)

式中:r(t)为分解的余项。

对任意一个信号x(t)可以使用EEMD方法将其分解为若干个平稳的本征模分量和一个余项。本征模分量代表着信号不同频段所具有的成分，一般不同的信号不同频段所具有的成分分布是不相同的，具有的能量分布也是不相同的。

图1为采集到的外圈故障的振动加速度信号，图2、图3为对该信号进行EEMD分解的结果。对采集到的外圈故障的振动加速度信号进行EEMD分解，获得8个本征模分量和1个余项。

图1 外圈故障振动加速度信号

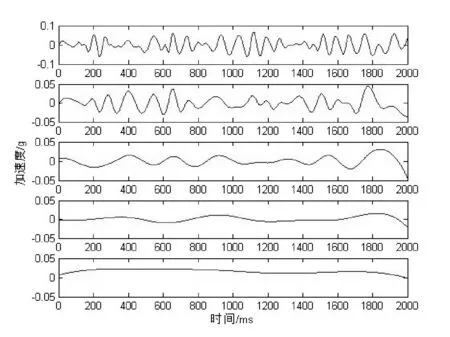
图3 外圈故障振动加速度信号EEMD分解结果

1.2 EEMD能量熵

轴承工作在正常状态或出现故障时，振动信号会不相同，振动信号中的能量在不同频段的分布也会不相同。通过EEMD方法将振动信号进行分解可以获得若干IMF分量，计算各个IMF的能量，获得振动信号中的能量分布，也就是能量熵。根据能量熵可以对轴承的工作状态进行判断。

使用EEMD方法对振动加速度信号x(t)进行分解可以获得n个IMF，计算得出各个IMF所具有的能量E1，E2，…，En。由于EEMD分解的结果具有正交性，余项所具有的能量较小，在对其忽略的情况下，各个IMF所具有的总能量和原始信号的能量应该相等。E1，E2，…，En表示信号不同频率成分所具有的能量，从而可以表示信号在不同频段的能量分布[10]。则EEMD能量熵可以如此定义。

(4)

式中，pi表示表示总能量中第i个IMF所具有的能量占的比重。

在正常状态下，轴承的振动相对平稳，振动信号的能量分布比较均匀，不确定性较高，所以轴承正常状态的熵值在三种情况中最高。当轴承出现故障时，由于故障的出现会导致能量在一定频率范围内集中，使得能量分布的不确定性减少，所以熵值也变小了。由于内圈故障相比外圈故障对信号影响的不同，内圈影响频率更高，所以内圈故障的能量熵值略大与外圈故障。

从上面可以看出，当轴承处于不同工作状态是振动信号的能量熵也会有变化，因此可以使用EEMD能量熵值来进行轴承工作状态的判断。使用不同工作状态的轴承振动信号的能量分布对相关向量机进行训练和学习，可以达到对轴承进行故障诊断的目的。

1.3 相关向量机

RVM的训练是在Bayes框架下进行的，使用先验参数的结构下基于主动相关决策理论来移除不相关的点，从而获得稀疏化的模型[11]。RVM可以用于向量回归问题和向量分类问题，在故障诊断问题中主要运用其分类理论。

RVM的计算模型与SVM相比最大的优点是是极大地减少了核函数的计算量。对于任意输入xi，RVM分类器计算模型为：

(5)

K(x,xi)=[1,k(x,xi),…,k(x,xn)]T

w=[ω0,ω1,…,ωM]T

式中:K(x,xi)为模型核函数向量其中i=1，2，…，M，w为模型的权值向量。相关向量机同支持向量机相比一个优点就是所选核函数不需要满足Mercer条件。

设ti服从独立分布，则其训练样本集的似然估计为：

(6)

t=[t1,t2,…,tn]T

对于新的输入向量x*其对应的目标向量t*的条件概率计算结果为：

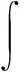
(7)

若使用最大似然法求解上式，易引起过适应问题，使模型的泛化能力减弱。为了解决这一问题，保障模型的稀疏性，相关向量机给每一个权值w分配了一个零均值高斯先验概率分布：

(8)

对上式进行反复迭代计算，求出所有的权值。忽略所有权值中近似零的权值，将剩余的非零权值作为训练向量输入，即保留相关向量。则式(6)可重写为：

(9)

2 基于EEMD和RVM的轴承故障诊断方法

将EEMD分解后得到的各个IMF的能量特征值作为相关向量机的输入。使用特征值对相关向量机进行训练，通过测试可以得知，使用EEMD方法和RVM基于能量熵的轴承故障诊断方法可以正确和高效地对轴承的工作状态进行诊断。故障诊断方法的基本实现流程为：采集轴承振动信号，对原始信号进行EEMD分解，计算获取到的IMF的能量分布，并将其输入相关向量机进行工作状态识别。

其具体步骤如下:

(1) 使用控制变量法，在轴承工作状态分别处于正常、内圈故障和外圈故障三种情况下，固定采样频率为f，分别进行N次振动信号采集，共得到振动信号样本3N个。

(2) 将采集到的振动信号按工作状态分为三组，对每组的每个振动信号进行EEMD分解，由于获得的IMF具有的特征越来弱，因此选择特征较强的前m个IMF来进行研究。

(3) 计算选中的IMF的能量：

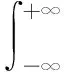
(10)

(4) 构建能量特征向量:

F=[E1,E2,…,Em]

(11)

将能量特征向量F进行归一化。

设：

(12)

则：

F′=[E1/E,E2/E,…,Em/E]

(13)

F′可作为相关向量机的输入。

(5) 建立由相关向量机组成的多故障分类器，由于需要识别三种工作状态，分类其由三个相关向量机组成。将轴承各个工作状态的特征向量作为输入，对相关向量机进行训练。

(6) 进行测试信号的采集，按照与步骤(2)-步骤(4)相同的方法获得特征向量，并将其作为故障分类器的输入，对故障分类器进行测试。

3 实验分析

本文的轴承数据来源为美国西储大学的轴承试验数据[12]。实验中使用加速度传感器采集振动信号。

表1为计算出的轴承不同工作状态振动加速度的能量熵值。可以看出，当轴承处于不同工作状态是振动信号的能量熵也会有变化。因此可以使用EEMD能量特征来进行轴承工作状态的判断。

表1 轴承不同状态的EEMD能量熵

分别选取30组工作状态为正常、内圈故障和外圈故障的轴承振动信号。分别在30组振动信号中随机选取20组，将其作为训练样本，并将剩余10组振动信号作为测试样本。

首先对训练样本信号进行EEMD分解，选择前6个IMF，计算EEMD能量特征向量。表2为训练样本的能量特征向量(由于空间问题，未将全部特征向量列出，每种状态仅列出4个，且特征值保留3位小数)。使用由训练样本获得的特征向量作为输入，对多故障分类器进行训练。最后使用测试样本对训练好的分类器进行测试。

表3为相关向量机组成的多故障分类器的测试结果。可以看出分类器对轴承工作状态判断的正确率很高。

表2 训练样本表

表3 分类器测试结果

表4为相关向量机与支持向量机和BP神经网络分类器的性能对比。在试验中训练样本个数为20，数据量较小，属于小样本情况。从表4中可以看出在小样本情况下，相关向量机的效率和准确度要优于支持向量机和BP神经网络。较高的效率说明相关向量机更适用于实时的诊断系统。

表4 性能比较

4 结 语

本文使用EEMD方法与相关向量机相结合的方法基于能量熵进行轴承故障诊断。首先使用EEMD方法对轴承振动信号进行分解并提取出能量特征，并将其输入由相关向量机组成的多故障分类器，对分类器进行训练和测试。通过对测试结果进行分析，可以得出以下结论：

(1) EEMD方法作为一种自适应的信号处理方法，非常适用于对轴承振动信号的处理。

(2) 基于EEMD能量熵可以对轴承的工作状态进行辨识。

(3) 相同方法下，相关向量机的效率和准确度要优于支持向量机和BP神经网络。

EEMD能量熵和相关向量机方法在轴承等机械零件故障信号处理和故障诊断方面有非常广阔的应用前景。将其应用在轴承等机械零件的故障诊断，可以及时发现故障，有效避免零件故障引起的重大事故，减少损失，降低生产成本。

[1] 裴峻峰,毕昆磊,吕苗荣.基于多特征参数和概率神经网络的滚动轴承故障诊断方法[J].中国机械工程,2014(15):2055-2058.

[2] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.

[3] Wu Z H,Huang N E.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[4] 王军辉,贾嵘,谭泊.基于EEMD和模糊C均值聚类的风电机组齿轮箱故障诊断[J].太阳能学报,2015(2):319-324.

[5] Mianji F A,Zhang Y.Robust Hyperspectral Classification Using Relevance Vector Machine[J].IEEE Transaction on Geoscience and Remote Sensing,2011,49(6):2100-2112.

[6] 吴小涛,杨锰,袁晓辉,等.基于峭度准则EEMD及改进形态滤波方法的轴承故障诊断[J].振动与冲击,2015,34(2):38-44.

[7] 李强,皮智谋.基于独立分量分析和相关向量机的轴承故障诊断研究[J].制造业自动化,2014,36(8):6-9.

[8] 王波,刘树林,张宏利,等.相关向量机及其在机械故障诊断中的应用研究进展[J].振动与冲击,2015,32(5):145-150.

[9] Zvokelj Matej,Zupan Samo,Prehil Ivan.EEMD-based multiscale ICA method for slewing bearing fault detection and diagnosis[J].Journal of sound and vibration,2016,370:394-423.

[10] 夏均忠,苏涛,张阳,等.基于EEMD能量熵及LS -SVM滚动轴承故障诊断[J].噪声与振动控制,2014(3):170-175.

[11] Tipping M E.Sparse Bayesian Learning and the Relevance Vector Machine[J].Machine Learning Research,2001,22(2):211-244.

[12] Case Western Reserve University Bearing Data Center.Seeded Fault Test Data[DB/OL].[2016-09-15].http://csegroups.case.edu/bearingdatacenter/home.

BEARINGFAULTDIAGNOSISMETHODBASEDONENERGYENTROPYOFVIBRATIONSIGNAL

Ren Yuqing Wang Hairui Qi Lei Li Rongyuan

(SchoolofInformationEngineeringandAutomation,KunmingUniversityofScienceandTechnology,Kunming650500,Yunnan,China)

There are a lot of bearings in mechanical equipment, which is the main reason of mechanical failure. Timely and accurate judgment of the bearing fault can effectively prevent the accident caused by the bearing fault and reduce the loss. A Bearing fault diagnosis scheme based on energy entropy is proposed in this paper. Different energy entropy of the bearing vibration signal has different energy distribution in different working condition. The state of the bearing can be judged by the difference of the energy distribution. First, original acceleration vibration signals are decomposed by ensemble empirical mode decomposition (EEMD) into a finite number of stationary intrinsic mode functions (IMFs). To identify the fault pattern and condition, energy feature extracted from a number of IMFs that contained the most dominant fault information could serve as input vectors of relevance vector machine. Practical examples show that the proposed diagnosis approach can identify bearing fault patterns effectively.

Ensemble empirical mode decomposition (EEMD) Energy entropy RVM Fault diagnosis

TP3

A

10.3969/j.issn.1000-386x.2017.09.055

2016-11-28。国家自然科学基金项目(61263023)。任玉卿，硕士，主研领域：嵌入式应用技术，网络控制技术。王海瑞，教授。齐磊，硕士。李荣远，硕士。