基于Gauss-Hermite分布模型的水印检测算法研究
李爱华 刘金华
1(南昌大学抚州医学院 江西 抚州 344000)2(电子科技大学电子工程学院 四川 成都 611731)
基于Gauss-Hermite分布模型的水印检测算法研究
李爱华1刘金华2
1(南昌大学抚州医学院 江西 抚州 344000)2(电子科技大学电子工程学院 四川 成都 611731)
图像水印的检测来源于统计信号处理的思想,其关键在于如何对图像经变换后的系数进行建模。在已有的水印检测模型中,图像基于高斯分布进行建模,容易导致在抗攻击条件下水印检测的性能较低。为克服这一不足,结合图像的视觉感知模型和高斯-埃尔米特(Gauss-Hermite)统计分布模型,提出一种数字水印的嵌入和盲检测方法。在水印嵌入中,以临界可见误差值JND(Just Noticeable Difference)作为水印嵌入强度,以提高水印的不可感知性。在水印检测中,基于高斯-埃尔米特分布对图像小波系数进行建模,并通过假设检验提出了水印的盲检测模型,最后推导了虚警概率和检测概率之间的工作特性关系。仿真结果表明:提出的水印检测模型在诸如噪声、JPEG压缩、滤波以及缩放等攻击下具有较好的性能。
水印检测方法 高斯-埃尔米特分布模型 视觉感知 工作特性曲线
0 引 言
多媒体数据的传播和发布丰富了人们的生活,拓宽了人们的视野,提升了人们的工作效率;但是,也给人们带来了诸如隐私泄露、产品版权纠纷、内容认证等方面的信息安全隐患。作为一种多媒体版权保护的有效手段之一——数字水印技术得到了人们深入的研究和关注[1-5]。
水印检测是数字水印技术中关键的组成部分。在数字水印检测中,一般将水印检测看成是统计信号的检测过程,即通过图像的统计分布模型对图像经变换后的系数进行建模。然后基于统计检测技术,推导出水印的检测阈值,以此来判定水印信息是否存在或将水印信息提取出来。常见的图像统计分布模型包括高斯分布模型、alpha分布模型、柯西分布、广义高斯分布模型等。一般来说,图像信号经离散余弦变换或小波变换后的系数特点体现为重尾分布,不满足高斯分布。为此,许多研究人员陆续提出了其他的统计分布模型,如文献[6-8]分别采用了广义高斯分布、柯西分布以及alpha分布模型来设计水印检测方法,并取得了较好的效果。但是,他们没有考虑图像数据的高阶矩特性,高阶矩是大于二阶的统计量,如三阶矩表示偏度,四阶矩表示峭度。在图像处理中,高阶矩可以更好地反映图像的边缘、轮廓等局部分布特征,具有较好的旋转不变性、尺度不变性和平移不变性。而图像的低阶矩,如一阶矩可以确定图像的质心,二阶矩可以反映图像矩阵在行或列上的方向性。但是这些低阶矩不能较好地描述图像的不变特征,因此,应用图像的高阶矩特性有助于提升水印抗常规图像处理和几何攻击的鲁棒性。
为此,本文首先基于视觉感知模型设计了一种水印嵌入方法。然后根据高斯-埃尔米特统计分布模型,结合高斯-埃尔米特分布模型[9]对图像小波子带系数的描述特性,运用小波子带样本数据的高阶矩特性,提出了一种水印的盲检测模型,并推导了虚警概率与检测概率之间的工作特性关系。最后基于标准的图像数据,通过仿真分析了水印检测模型在抗攻击的性能。
1 数字水印嵌入
1.1 视觉感知模型
根据视觉感知特点,若水印的信号强度低于图像的临界可见误差值,那么人眼视觉感知系统将感觉不到原始图像中嵌入了水印信号,水印的不可感知性受到频率、亮度以及纹理等特性的影响[10],嵌入因子的计算需要综合这些因素的影响。
(1) 频率敏感度函数可表示为:
(1)
其中s=1,2,3,4为经小波分解的层数,o表示分解的方向,o∈{LL,LH,HL,HH}。F(s,o)为第s个子带上、方向为o的频率敏感度值。
(2) 亮度敏感度函数:根据视觉感知模型,背景越亮或越暗的区域能隐藏更多的水印信号。亮度敏感度函数可以表示为:
(2)

(3)
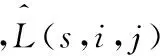
(3) 纹理敏感度函数:纹理敏感度函数可以表示为:
T(s,i,j)=
(4)
综合式(1)-式(4),可得JND估计值为:
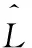
(5)
根据视觉感知模型,定义每个小波系数的嵌入强度因子:
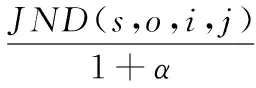
(6)
其中α∈[0,2]表示调节参数。
1.2 水印嵌入
基于乘性嵌入方式嵌入水印,其详细步骤如下:
1) 将原始图像划分成互不重叠的子块。然后计算每个图像子块的图像熵,并按熵值降序排序,选取前K个熵值较大的图像子块作为水印嵌入区域。
2) 采用DWT对图像子块进行分解,分解层数选为3层。
3) 选取第3层中的小波子带系数,记为f={fij|(i,j)∈Ω},其中Ω表示小波子带所在的图像区域。水印信号为:wij=λijνij,其中νij由伪随机生成器生成的水印序列,如{-1,1}。λij表示图像临界可见误差值生成的水印嵌入因子,并根据式(6)计算。水印的嵌入过程可表示为:
yij=fij+wij=fij+λijνij
(7)
其中yij表示嵌入水印后的小波系数。
4) 重复步骤2)和步骤3),然后将所有嵌入水印的图像子块与未嵌入水印的图像子块进行组合,最后采用小波逆变换对组合的图像进行重构,最终得到嵌入水印后的图像。
2 水印检测模型
2.1 高斯-埃尔米特分布
小波子带系数的统计分布一般不满足高斯分布,为此,根据Gauss-Hermite模型[9]来描述小波子带系数的统计特性。Gauss-Hermite模型的概率分布函数为:
(8)
其中f表示一个小波子带中所有小波系数形成的向量,fi,j表示原始图像在空间位置(i,j)下的小波系数。pf(f)表示随机向量f的概率密度函数,σf表示随机向量f的标准方差,Hr(f)表示r阶Hermite多项式,其特征为:
H0(f)= 1H1(f)=fHr+1(f)=fHr(f)-rHr-1(f)r≥1
(9)
在式(8)中,βr可根据i阶距Mif[11]计算:
(10)
其中x表示小于或等于x的最大整数。在统计理论中,随机变量X的k阶矩定义为MK=E[(X-E(X))K],E(·)表示期望算子。式(10)中小波系数向量f的i阶距Mif的计算[11]为:
(11)
其中g=f+ε,ε表示噪声信号,g表示原始小波系数向量f在加性噪声条件下的信号。Mig为g的i阶矩,M(i-2u)f为f的(i-2u)阶矩,M(2u)ε为ε的(2u)阶矩。odd和even分别表示奇数和偶数。式(11)中Miε的计算为:
(12)
其中σ为噪声信号ε的标准方差。
2.2 水印检测
水印的检测采用对数极大似然方法,根据式(7)可得:
(13)
其中H0表示零假设,即没有检测到水印信息;H1表示备择假设,即含有水印信息,λ表示水印嵌入因子。进一步,式(13)等价于:
(14)
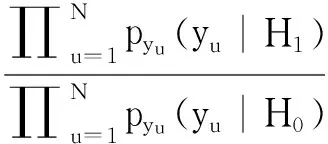
(15)
其中pfa表示虚警概率,pm表示漏警概率。pr(H0)表示零假设概率,pr(H1)表示备择假设概率。τ表示检测阈值。为更好地描述图像子带系数的分布特性,对高斯-埃尔米特分布模型[11]进行改进,对数极大似然率的计算可进一步表示为:
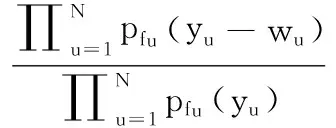
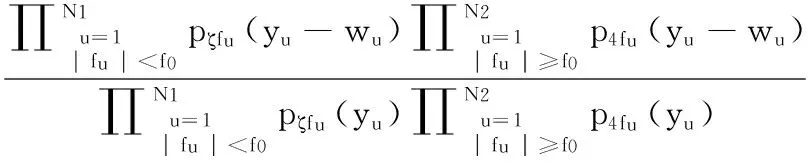
(16)
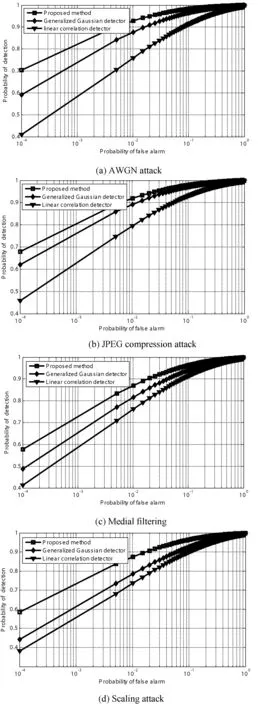
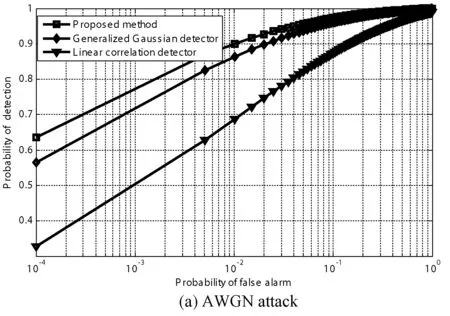
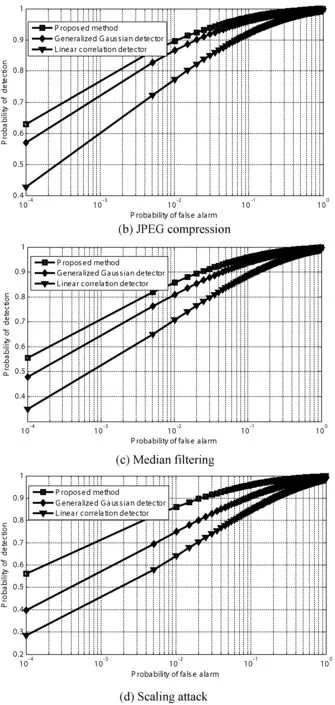
其中N=N1+N2,N1、N2分别是fu 从式(16)可以看出,对数极大似然率lnΛ(y)是大量统计独立的随机变量之和,由中心极限定理可知,lnΛ(y)满足高斯分布。为推导ROC关系,需要估计分别在零假设H0和备择假设H1下的均值和方差。为不失一般性,在零假设H0下,均值和方差分别为: μΛ0=Ew[lnΛ(y)|H0]= (17) (18) Ew[lnΛ(y)|H0]2= (19) 与在零假设H0条件下类似,在备择假设H1条件下的均值和方差分别为: μΛ1=Ew[lnΛ(y)|H1]= (20) (21) Ew[lnΛ(y)|H1]2= (22) 综合式(17)-式(22),可得: (23) 进一步,在盲检测过程中,设零假设H0和备择假设H1的概率相等,即pr(H0)=pr(H1)。对于水印检测阈值τ,虚警概率和检测概率可分别表示为: (24) τ=μΛ0+σΛ0Q-1(pfa) (25) 进一步,可得水印检测概率与虚警概率之间的关系为: (26) 令SNR可得水印的工作特性曲线关系为: (27) 仿真中选用了Lena和Boat两幅图像作为研究对象,图像大小均为512×512。图像子块的大小设置为32×32,子块总数为256。计算每个图像子块的熵大小,选择前64个熵较大的图像子块作为水印嵌入空间。选取图像子块后,采用DWT对每一个图像子块进行小波分解,提取64个小波系数嵌入水印,即每个图像子块嵌入的水印容量为64,而分解的图像子块数为256,所以总的嵌入水印容量为64×256,即16 384。 图1和图2分别给出了两幅图像的水印嵌入结果。其中左边部分表示原始图像,中间部分表示嵌入水印后的图像,最右边部分表示原始图像与嵌入水印后图像之间的差值图像。通过MATLAB7.10仿真计算,两幅图像在嵌入水印后的图像与对应原始图像之间的峰值信噪比PSNR(peak signal-to-noise-ratio)均超过了45 dB。从图1和图2中可以看出,嵌入水印后图像具有较好的不可感知性。其原因是由于算法综合应用了视觉感知和图像的熵特性。一方面基于小波视觉感知模型对水印嵌入因子进行了考量,使得水印的信号强度低于图像的临界可见误差值。另一方面利用了熵在图像灰度方面的聚集分布特性,使得水印信息沿着图像中灰度密集度较为丰富的区域进行嵌入(可以从差值图像看出),可以较好地隐藏水印信息。 图1 对Lena图像嵌入水印后的结果 图2 对Boat图像嵌入水印后的结果 图3和图4分别给出了Lena和Boat图像在AWGN、JPEG压缩、中值滤波以及幅度尺度缩放攻击下本文算法与文献[6,10,12]下的水印检测性能比较结果。为什么和文献[6,10,12]进行对比而不和其他方法进行对比,其一是因为文中的重点是水印的检测,一般都是采用统计处理方法来检测图像中的水印。文献[6,10,12]都是基于相应的统计检测理论来分析水印信息,与本文的主题一致。为突出高斯-埃尔米特分布模型较好的性能,所以与文献[6,10,12]进行了相关比较。其二是文中采用的变换与文献[6,10,12]采用的变换较为类似,都是小波变换、离散余弦变换之类。文献[6]与文献[12]采用的水印检测器为广义高斯检测器,而文献[10]采用的水印检测器为线性相关检测器。在抗攻击测试中,加性噪声攻击中噪声方差为20,JPEG压缩质量因子70%,中值滤波窗口大小为5×5以及缩放尺度比例为0.5。从图3和图4中均可以看出,在相同的虚警概率下,本文算法的检测性能均优于广义高斯检测器和线性相关检测器的性能,主要原因归纳为: (1) 数字水印检测器基于高斯-埃尔米特分布模型,该模型利用了图像小波系数的高阶矩特性,图像高阶矩具有较好的尺度不变性以及变换不变性等优点,使得高斯-埃尔米特分布模型能够更好地拟合小波系数,较好地描述图像的边缘、纹理等局部特征,有效提高了水印在抗攻击条件下的检测性能。 (2) 应用了图像熵的物理意义,选取了图像中熵值较大的区域作为水印嵌入空间,并在图像子块中低频子带区域嵌入水印,同时结合了视觉感知模型,在满足水印不可感知性的同时,提升了水印系统的鲁棒性,增强了水印抗攻击的能力,相应的水印检测性能较好。 图3 水印检测性能比较结果(Lena) 图4 水印检测性能比较结果(Boat) 综合应用视觉感知模型和高斯-埃尔米特分布方法,提出了一种小波域数字水印嵌入和盲检测模型,重点对水印的检测性能进行了分析和讨论。基于高斯-埃尔米特模型对图像的小波系数进行统计建模,并结合统计信号处理理论,讨论了水印系统虚警概率与检测概率之间的工作特性关系,并给出了水印的检测阈值。提出的算法具有以下特点: 1) 较好地综合了图像的视觉感知模型求出视觉掩码,即图像的临界可见误差值JND值,并与伪随机生成器相结合,产生相应的水印信号。提高了水印的不可感知性。 2) 以高斯-埃尔米特分布模型刻画小波系数,利用了图像的高阶矩特性,较好地描述图像的局部特征,给出了水印系统的盲检测模型,提高了水印系统的检测性能。 3) 综合应用了图像的视觉感知模型和熵的含义,利用了熵在图像灰度分布的聚集特性,较好地平衡了水印系统不可感知性与鲁棒性之间的矛盾,提升了水印的抗攻击能力。 [1] Li X,Sun X,Liu Q.Image Integrity Authentication Scheme Based on Fixed Point Theory[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2013,24(2):632-645. [2] Guo J M,Lai G H,Wong K,et al.Progressive halftone watermarking using multilayer table lookup strategy[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2015,24(7):2009-2024. [3] Sarreshtedari S,Akhaee M A.A Source-Channel Coding Approach to Digital Image Protection and Self-Recovery[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2015,24(7):2266-2277. [4] Urvoy M,Goudia D,Autrusseau F.Perceptual DFT Watermarking With Improved Detection and Robustness to Geometrical Distortions[J].IEEE Transactions on Information Forensics & Security,2014,9(7):1108-1119. [5] Zareian M,Tohidypour H R.A Novel Gain Invariant Quantization-Based Watermarking Approach[J].Information Forensics & Security IEEE Transactions on,2014,9(11):1804-1813. [6] Wang J,Sun X,Zheng Y,et al.Hybrid Additive Multi-watermarking Decoder[C]//Fourth International Conference on Multimedia Information NETWORKING and Security.IEEE Computer Society,2012:666-669. [7] Cheng Q,Huang T S.Robust optimum detection of transform domain multiplicative watermarks[J].IEEE Transactions on Signal Processing,2003,51(4):906-924. [8] Sadreazami H,Ahmad M O,Swamy M N.A study of multiplicative watermark detection in the contourlet domain using alpha-stable distributions[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2014,23(10):4348-4360. [9] Rahman S M,Ahmad M O,Swamy M N.A new statistical detector for DWT-based additive image watermarking using the Gauss-hermite expansion[J].IEEE Transactions on Image Processing,2009,18(8):1782-1796. [10] Djukanovic S,Djurovic I.Detection optimization for the DCT-domain image watermarking system[C]//Signal Processing Conference,2010,European.IEEE,2010:830-834. [11] Rahman S M,Ahmad M O,Swamy M N.Bayesian wavelet-based image denoising using the Gauss-Hermite expansion[J].IEEE Transactions on Image Processing,2008,17(10):1755-1771. [12] Mairgiotis A K,Galatsanos N P,Yang Y.New Additive Watermark Detectors Based On A Hierarchical Spatially Adaptive Image Model[J].IEEE Transactions on Information Forensics & Security,2008,3(1):29-37. AWATERMARKDETECTIONALGORITHMBASEDONGAUSS-HERMITEDISTRIBUTIONMODEL Li Aihua1Liu Jinhua21 (FuzhouMedicalCollegeofNanchangUniversity,Fuzhou344000,Jiangxi,China)2(SchoolofElectronicEngineering,UniversityofElectronicScienceandTechnologyofChina,Chengdu611731,Sichuan,China) The detection of image watermarking comes from the idea of statistical signal processing. Its key point is how to model the transformation coefficient of an image. In the existing detection model, the coefficient of image is modeled by Gauss distribution, which results in the low performance of watermark detection under attack. In order to address this issue, a watermark embedding and blind detection method was proposed by combining the visual perceptual model and Gauss-Hermite distribution model. To improve the invisibility of watermarking, Just Noticeable Difference was used as the watermark embedding strength factor during the embedding process. In the process of watermark detection, the image wavelet coefficients were modeled by Gauss-Hermite model, thus the blind watermark detection method was proposed. Finally, the Receiver Operating Characteristic (ROC) curve between the probability of false alarm and the probability of detection was derived and discussed respectively. Experimental results demonstrate that the proposed method has better performance under attack such as AWGN, JPEG compression, filtering and scaling. Watermark detection method Gauss-Hermite distribution model Visual perceptual Receiver operating characteristic TP391.41 A 10.3969/j.issn.1000-386x.2017.09.043 2016-11-23。李爱华,讲师,主研领域:图像处理。刘金华,高工。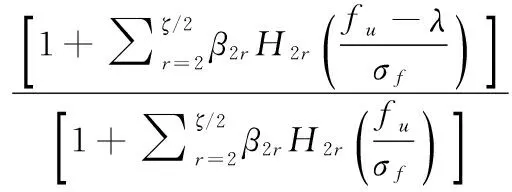
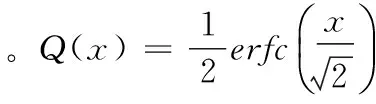
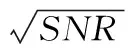
3 仿真结果与分析


4 结 语

