基于偏相关系数的脑功能连接分析

黄晓霞 何红霞

(上海海事大学信息工程学院 上海 200135)

基于偏相关系数的脑功能连接分析

黄晓霞 何红霞

(上海海事大学信息工程学院 上海 200135)

大脑是一个具有高度复杂性的信息处理系统，拥有丰富且复杂的结构与功能，其功能的执行主要依赖于脑功能区之间的相互作用所构成的网络实现。研究采用偏相关系数分析方法，在阈值的设定研究基础上，进一步引入节点度的概念，用于反馈节点之间连接强度的大小。对13例精神分裂症患者和24例正常人在静息态下273个通道的脑磁(MEG)信号进行分析，探索正常组与患者组之间脑功能连接的差异性。研究表明精神病患者在大部分脑区有显著的功能连接，在额叶和颞叶以及脑边缘部分与正常人有显著性差异，推测这些异常连接区域有可能与精神分裂症的病理有关。

MEG信号 静息态 脑功能连接 偏相关系数 节点度

0 引 言

担任高级指挥官角色的大脑一直是科学家们不懈研究的重要领域[1]。大脑的静息态是指未作任何主动思维活动，清醒放松的状态，是大脑所处的各种复杂状态中最基础和最本质的状态, 是普遍采用的一种基线状态[2]。国内外众多研究脑功能连接的方法主要是基于脑信号数据的分析[3]，其中大尺度脑功能连接的分析中多采用fMRI和MEG进行分析[4]。脑区间的相关属性称为“功能连通性”或“内在连接”[5-6]。功能连接指的是空间上相距较远的神经生理事件之间的时间相关性，是通过计算不同脑区时间序列在时间上的统计依赖性，来探讨不同脑区活动的同步性[7]，Sakkalis[8]将脑功能连接的度量分为线性、非线性和基于信息的三类方法。线性方法包括时域分析中的皮尔森相关、偏相关系数以及频域分析中的相干、偏相干系数等；非线性方法主要有同步似然性SL(Synchronization Likelihood)、锁相值PLV(Phase Locking Value)；基于信息的方法有交叉互信息CMI(Cross Mutual Information)等[9]。本文采用偏相关系数对正常人和精神分裂症患者在静息态下的脑磁信号MEG进行分析，构建脑功能连接网络，以期发现患者组和正常组实验对象的脑功能网络连接的差异性，为下一步探究可能的发病病因打下基础。

1 实验数据及方法

1.1 数据来源

本文的实验数据是由美国国立精神卫生研究所MEG 科研平台提供。利用加拿大VSM MedTech 公司CTF-275 超导量子干涉仪(SQUID)的全头型脑磁图设备，获取精神分裂症患者和正常人两组实验组对象在静息态下的脑磁(MEG)数据。本文选取了13例精神分裂症患者和24例正常人的MEG信号，由于F43和O13通道损坏，实际分析的MEG数据包含了273个通道，采样频率为600 Hz，采样时间4分钟。

1.2 偏相关系数

当两个变量同时与第三方变量存在相关性时，由于变量之间两两存在关系，如果只考虑到其中两个变量的相关性系数，则不能足够准确地反应出二者之间的联系。以本文研究数据为例，对于通道5与通道6的MEG信号来说，通道5可能不仅仅影响通道6，通道6可能被通道5和其他若干个通道同时影响。因此想要更加准确研究这273个通道之间的相关程度，发现脑功能连接的特性，就需要排除其他干扰变量的影响。

偏相关系数是在排除了其他变量的影响下计算变量间的相关系数的一种相关性研究方式，其中偏相关系数的绝对值越大则表明相关性越强，反之相关性越弱[10]。本文采用该方法，以此排除第三方通道信号的干扰，计算任意两个通道相关性。

偏相关系数计算方法主要有以下三种[10]：

(1) 迭代法：可以认为简单相关系数为0阶偏相关系数，任何n阶偏相关都可以通过3个(n-1)阶偏相关系数计算出来。公式如下：

(1)

(2) 线性回归法：假设我们需要计算X和Y之间的相关性，Z代表其他所有的变量，X和Y的偏相关系数可以认为是X和Z线性回归得到的残差Rx与Y和Z线性回归得到的残差Ry之间的简单相关系数，即Pearson相关系数。

(3) 相关矩阵求逆法：

首先求得相关矩阵：

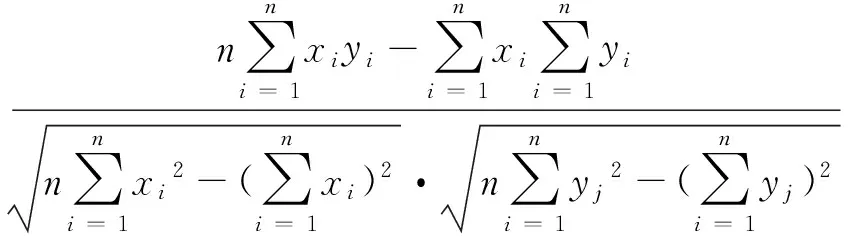
(2)

再对相关矩阵求得协方差矩阵，并求它的逆矩阵：

X=Cov(R)r=(rij)=(X)-1

(3)

其中X是所有变量的协方差矩阵，r是协方差矩阵的逆。偏相关矩阵计算为：

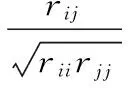
(4)

本文采用第三种相关矩阵求逆法，相对于其他两种更加方便简洁。

2 实验及结果分析

2.1 预处理

考虑到心跳和眼动信号等干扰，对两组实验对象MEG数据进行带通滤波(0.5～30 Hz)去除部分噪声，然后利用盲源信号分离技术对其进行独立成分分析(ICA)，剔除眼电、心电等各种伪迹，最终获得相对干净的数据。

2.2 偏相关系数计算

本次分析数据，包含13例精神分裂症患者和24例正常人的共37组静息态下的测试数据，每组数据由273个通道，每个通道由14 400个时间序列点组成。每个通道的信号数据作为一个独立的信号变量，共273个变量，每个通道所包含的时间序列点作为每个变量中所包含的所有数据集合，对这273个信号变量两两作偏相关计算，得到规模为273×273的偏相关系数矩阵，在此偏相关系矩阵中，若系数值>0，则表示通道之间呈正相关，反之则表示通道之间呈负相关。图1为正常组和患者组各自对应的偏相关系数均值矩阵图，两组实验对象的偏相关系数值均分布于-0.5～1之间，系数值的大小通过由深至浅的颜色映射。由图1可看出，患者组图中大部分颜色比正常组的颜色更浅，且小部分偏相关系数值更是接近于1，说明总体上患者组比正常组具有更大的偏相关系数值。

图1 实验对照组

2.3 阈值选择

2.3.1 三大原则

阈值的作用是将偏相关系数矩阵转换为二值矩阵。从网络结构的角度来看，阈值的选择需满足以下三条准则[11-12]：(1) 大脑网络应该是一个稀疏网络，且是一个连通图，因此大脑中不存在孤立的与其他无联系的脑区；(2) 大脑的平均度值K>2ln(N) ；(3) 大脑网络密度D<50%，研究表明[12]脑网络是一个低耗网络，其稀疏度一般<0.5。

假设阈值设定为r，对应偏相关系数矩阵元数值rij，若|rij|≥r，则对应的二值矩阵A中aij=1 ，否则aij=0 ，公式如下：

(5)

得到的二值矩阵对应节点为273的脑功能网络连接图，矩阵中aij=1，表示通道i和通道j有连接，aij=0，则表示通道i和通道j无连接。

2.3.2 阈值选择结果

上述的三条准则，第(1)条是为了保证网络的完整性，它要求阈值不能过高；第(2)条是为了满足小世界特性；第(3)条则是限制阈值不能过低，以符合实际大脑高效的特性。本文实验中，阈值范围设置在0～0.2之间，调节阈值跨度为0.005，根据不同的阈值计算不同的网络平均度K和网络密度D，计算公示如下：

(6)

(7)

其中，M表示网络所有节点的度的和，N表示网络节点总数，从而得到两组实验对象的网络平均度和网络密度的对比如图2所示。

图2 正常组和患者组网络密度、网络平均度值对比图

由图2可看出，当阈值约在0.06处时，正常组与患者的网络密度和网络平均度差异性更大。设定阈值r=0.06，由此生成正常组和患者组的二值矩阵，其对应的灰度图如图3所示。图中白色区域对应二值矩阵中值为1的部分，表示通道之间有连接；黑色区域对应二值矩阵中值为0的部分，表示通道之间无连接。统计可得，患者组网络和正常组网络均包含273个节点，且患者组网络共计23 562条边，正常组网络仅14 806条边，说明患者组通道之间的连接更加紧密，其脑功能连接性更强。

图3 阈值为0.06时正常组和患者组二值矩阵对比图

2.4 脑网络功能分析

进一步引入节点度的概念，节点的度是指和该节点相关联的边的条数，又称关联度，是反映节点属性的一个重要指标[1]。本文中是指通道与通道之间相关联的边的条数。

将273个通道所对应的二值矩阵视为脑网络的连接图，每个通道作为一个单独的节点，二值矩阵中aij=1，则表示对应两个通道之间有连接。对矩阵每一行作求和运算，即求得脑网络连接图中每个节点的节点度，节点度的大小表明了与之连接的通道个数的多少。节点度越大，表明该节点在脑网络中的地位越重要。

实验将273个通道划分为：MLC、MLF、MLO、MLP、MLT、MRC、MRF、MRO、MRP、MRT、MZ等11个脑区(MZ是中间竖线脑区通道)，L表示左，R表示右，F为额叶，C为中央区，P为顶叶，O为枕叶，T为颞叶，并统计各脑区的节点度的和。图4为MEG感兴趣区皮层示意图及其对应脑区的节点度统计值表。

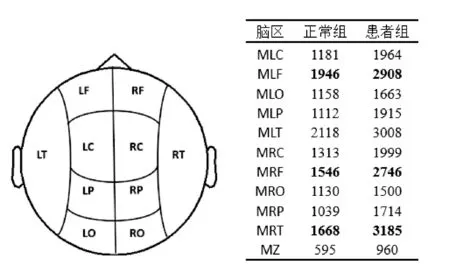
图4 MEG感兴趣区皮层示意图及其对应节点度表格

由图4可看出，节点度在11个脑区的总体分布上患者组比正常组明显要大，尤其在额叶区(MLF，MRF)以及右颞叶区(MLT，MRT)患者组更加明显。说明脑区对应的大部分通道节点在脑网络中精神分裂症患者组较正常组占更重要的地位。

进一步利用两组样本中273个通道的节点度值绘制成散点图以及全头拓扑图。

图5显示了患者组与正常组通道节点度的散点对比图，患者组节点度值分布在[7,143]，而正常组的节点度值分布在[10,122]，且患者组的通道节点度值明显普遍大于正常组。说明静息态下，患者组在差异通道所对应的脑区功能连接强度较正常组更大，脑区活跃程度较正常组更高。

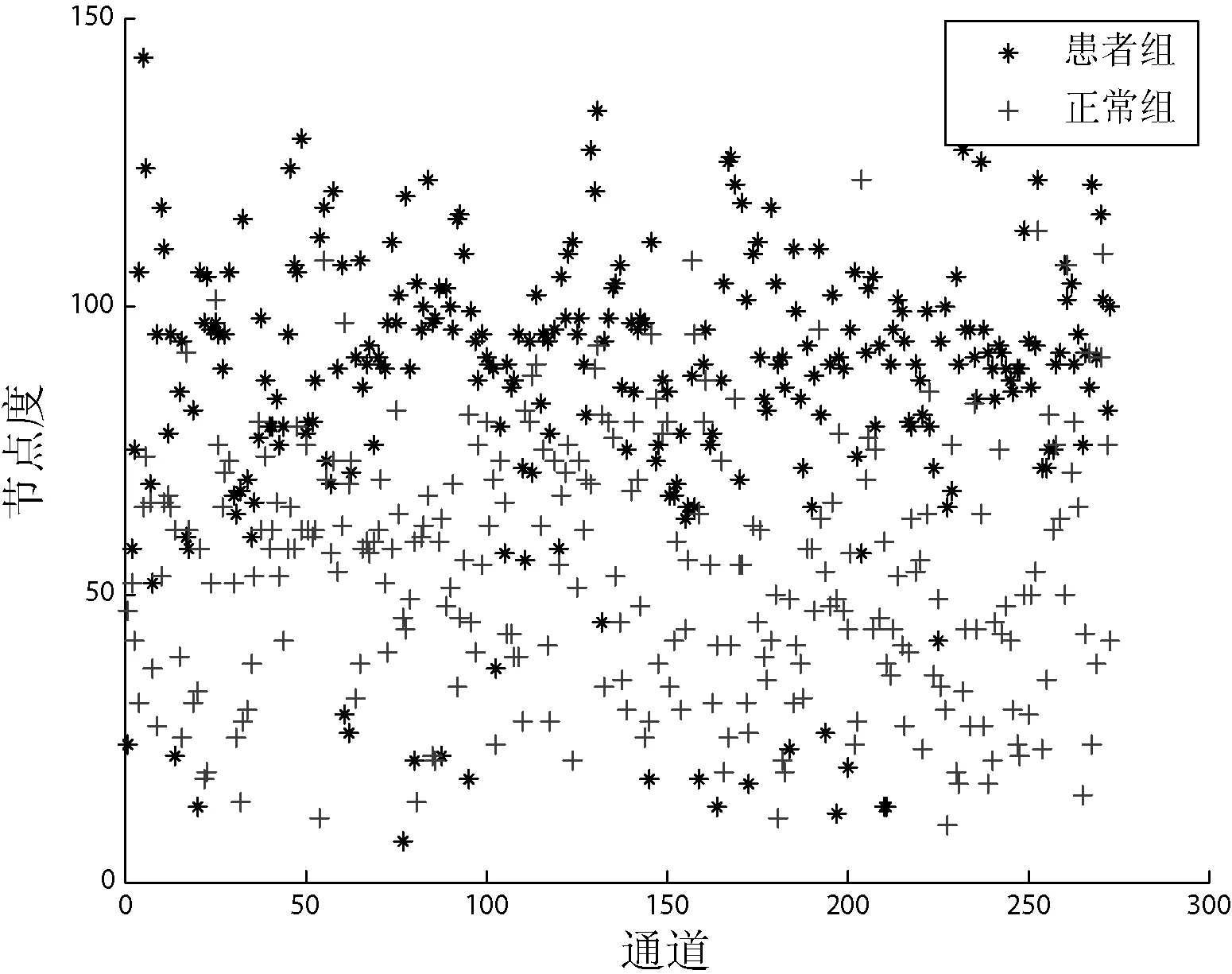
图5 患者组与正常组通道节点度的对比图

由全头拓扑图6可以看出，两组实验对象的通道节点度值的分布有着明显的差异性。较大的节点度值在患者组的拓扑图中分布更广，说明患者组在这些对应的通道脑区的功能连接强度大于正常组。结合图4中节点度统计表以及图6可看出，尤其是在额叶区以及右颞叶区两组实验对象的通道节点度值差异更为明显。虽然在额叶区有小部分正常组的通道节点度值比患者组的大，但总体上，在额叶区、右颞叶区以及脑边缘区患者组的通道节点度值明显大于正常组，其对应的脑功能连接强度明显高于正常组。这可能与静息态下精神分裂症患者的脑区活动较正常人更加活跃、分散、混乱有关。

图6 正常组和患者组节点度值全头拓扑图

3 结 语

本文采用偏相关系数分析方法对正常组和患者组静息态下的MEG信号进行分析，以273个通道信号两两作为研究变量，排除第三方通道信号的干扰，探究正常组与患者组的脑功能连接的差异性。研究发现精神分裂症患者和正常人的脑功能连接有着一定的差异。表现在大部分脑区精神分裂症患者的脑功能连接强度明显大于正常人，尤其在额叶区、右颞叶脑区以及脑边缘部分更为明显，说明静息态下精神分裂症患者的脑区活动较正常人更加活跃与混乱。结论：这些精神分裂症患者功能连接异常的脑区很有可能与其发病机制有关。另外，有研究结果显示：精神分裂症患者的部分脑区存在异常现象，在额叶、颞叶和边缘脑区尤为明显[13]，且患者脑灰质体积减少主要存在于额叶、颞叶等脑区中[14]。本文从脑功能连接的角度得出的研究结果与上述结论相吻合，说明有关区域的异常将导致正常人和精神分裂症患者在功能连接方面的异常。该研究成果有望为研究精神分裂症患者的发病机理和临床诊断提供新的思路与方向。

本文研究尚存在一些不足，实验数据并不足够多。由于精神病征的多差异性，各种疾病和认知功能所反映的脑网络连接特征规律有待深入研究，症状不同或患病程度不同都有可能影响实验最终结果，因此实验的普遍性有待进一步研究验证。

[1] 付灵弟,徐桂芝,郭苗苗,等.基于脑电和磁刺激的脑功能网络研究[J].纳米技术与精密工程,2015(5):359-365.

[2] 杨剑,陈书燊,皇甫浩然,等.静息态脑电信号动态功能连接分析[J].物理学报,2015(5):374-383.

[3] Marrelec G,Bellec P,Benali H.Exploring large-scale brain networks in functional MRI[J].Journal of physiology,Paris,2006,100(4):171-181.

[4] Schnitzler A,Gross J.Functional connectivity analysis in magnetoencephalography[J].International Review of Neurobiology,2005,68(1):173-195.

[5] Biswal B,Yetkin F Z,Haughton V M,et al.Functional connectivity in the motor cortex of resting human brain using echo-planar mri[J].Magnetic Resonance in Medicine,1995,34(4):537-541.

[6] 刘慧华,郑金瓯.静息态功能磁共振方法学的研究进展[J].医学综述,2016,22(1):136-140.

[7] Wang L,Laviolette P,O′Keefe K,et al.Intrinsic connectivity between the hippocampus and posteromedial cortex predicts memory performance in cognitively intact older individuals[J].Neuroimage,2010,51(2):910-917.

[8] Sakkalis V.Review of advanced techniques for the estimation of brain connectivity measured with EEG/MEG[J].Computers in Biology & Medicine,2011,41(12):1110-1117.

[9] 唐海英.基于偏相干系数的脑功能连接研究及其在癫痫诊断中的应用[D].南京理工大学,2013.

[10] 胡云奉.基于图论的脑连接关系构建与分析[D].华东理工大学,2014.

[11] 陈旭辉,焦静静,柯铭,等.静息状态下脑网络建模及功能连接特性[J].兰州理工大学学报,2010,36(5):88-92.

[12] 薛绍伟,唐一源,李健,等.一种基于fMRI数据的脑功能网络构建方法[J].计算机应用研究,2010,27(11):4055-4057.

[13] Robyn H,Crow T J,Dick P,et al.Regional deficits in brain volume in schizophrenia:a meta-analysis of voxel-based morphometry studies[J].American Journal of Psychiatry,2006,162(12):2233-45.

[14] 胡茂荣.精神分裂症认知、脑灰质和白质内表型研究[D].中南大学,2012.

ANALYSISOFBRAINFUNCTIONBINDINGBASEDONPARTIALCORRELATIONCOEFFICIENT

Huang Xiaoxia He Hongxia

(CollegeofInformationEngineering,ShanghaiMaritimeUniversity,Shanghai200135,China)

The human brain is an information processing system of high complexity with complex structure and various functions which is mainly dependent on the network composed of the interaction between brain regions. This paper adopts partial correlation coefficient analysis with a threshold setting to get a further introduction called node degree. Its value can tell us the connection strength between nodes, we used it to analyze 273 brain magnetic signal channels (MEG) under resting state in 24 healthy subjects and 13 cases of mental patients. Explored the difference between their brain function bindings. Studies have shown that patients with mental disease have more connection between brain areas, there is a significant difference in the frontal and temporal lobes and the limbic portion of normal subjects. We suppose that these abnormalities are related to schizophrenia.

MEG signals Resting state Brain function binding Partial correlation coefficient Node degrees

TP3

A

10.3969/j.issn.1000-386x.2017.09.021

2016-09-29。黄晓霞，副教授，主研领域：脑波信息处理与脑机接口，智能信息处理。何红霞，硕士。