数形结合,建构运算律的基本模型
胡芳
[摘 要]小学阶段,运算律是运算教学的难点之一,尤其是乘法分配律。教材中,简便运算的题型与计算的练习量都偏少,通过对学生错例的分析,给出相应的教学策略,以帮助学生掌握乘法分配律。
[关键词]乘法分配律;简便运算;数形结合;模型
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)26-0021-02
数学教材中,知识点的编排往往承袭两个顺序,一是数学知识内在的逻辑顺序,二是学生认知发展的顺序。人教版教材把简便运算编排在四年级下册,除了五条基本运算定律外,连减、连除的简便计算及加、减、乘、除的灵活应用等相关内容也编排在同一单元。这样的编排与系列位置效应理论是相悖的,因为心理学系列位置效应理论指出:“如果学习材料中各部分的位置不同,学习效果就不同。”乘法分配律与乘法结合律在形式上较为相似,这两个内容的例题和引入方式也十分相似,学生在学习时会混淆是情理之中的事。
在学习完一节课的内容后,学生都能较好地理解运算定律,大部分学生还能根据运算定律举一反三,但是在学习整个单元的内容后,学生做题时就会出现五花八门的错误:有的学生只是盲目地套用,没有进行客观的分析和思考;有的学生的简便运算意识薄弱,不知道如何灵活运用;有的学生混淆定律,张冠李戴,对定律认识不深刻。
对此,在每个单元的学习结束后,我专门安排一节课来帮助学生纠正易错题,我称这样的课为“晒错题”课。“晒错题”可以放大错误,把易错题集中在一起,让学生任意选择,然后分析易错题、寻找错因、猜测做题者的想法,进而从根源上深刻认识运算定律的本质。
【错例一】乘法结合律和乘法分配律的形式较为接近,相似的题型会干扰学生,导致出现负迁移。如(8×4)×125=(8×125)×(4×125)。
【错例二】盲目运用“凑整思想”,导致学生的简便计算意识出现混乱。如578-36+64=578-(36+64)。
【错例三】在练习中渗透较少的定律,学生容易忽略,从而造成错误。如482-(82-35),去掉括号应变成482-82+35,很多学生却写成482-82-35;又如45+55-45+55,应该带着符号“搬家”,变成45-45+55+55=110,但有的学生遗漏了符号,写成45+55-45+55=100-100=0。
【错例四】25×32×125=(25×4)+(8×125);
27×99=27×(99+1)=27×100=2700;
25×(40+4)=25×40+4。
分析学生的表现和出错的原因,我总结出两点:一是学生对运算定律内涵的理解只停留在浅表层次,虽能理解但缺乏结构化的认识;二是对运算定律内涵的理解只停留在工具性理解层面,缺乏关系性的理解。
因此,在简便运算中不能只看到“数”,只想到“算”,还要想到运算定律的本质内容。通过以形表数,让学生观察数与形的一一对应的关系,可促进学生认识运算律的本质。在教学中,教师要将直观的“形”与抽象的“数”对应起来,以形表数,建构运算定律的直观模型,是使学生最终掌握抽象运算定律的必经过程。
在教学“乘法分配律”时,我调整了原有的教学方案:先出示教材情境图,再从现实原型出发,给出计算实例,解释算理,然后采用数形结合的方式让学生看图想算式、看算式画图、看公式想象,从而抽象出乘法分配律的字母公式,帮助学生建立几何模型。
题目:有25组学生参加了植树活动,每个小组均有4个男学生和2个女学生,求一共有多少名学生参加了这次植树活动。
方法一:(4+2)×25=6×25=150。
方法二:4×25+2×25=100+50=150。
由此可知,(4+2)×25=4×25+2×25,利用不同的算式得到相同答案直观展示了乘法分配律的本质,教学水到渠成。
我还利用数形结合的方法渗透几何模型的结构。
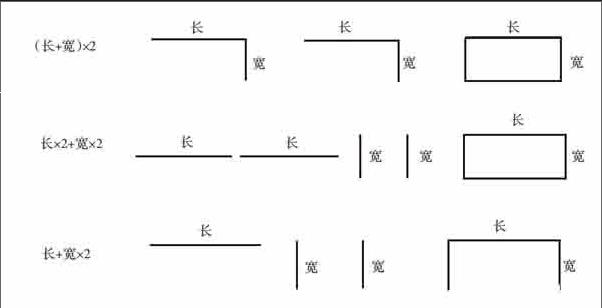
四(1)班栽树的地点是一块长5米、宽3米的长方形平地。请用两种方法求这块长方形平地的周长。

在学生得出“5×2+3×2=16”和“(5+3)×2=16”后,我要求学生指出式子中的每一步运算对应的是图上的哪一部分,让学生感受图形与数的一一对应关系,这样学生就很容易理解“5×2+3×2=(5+3)×2”的意义。随后,我引导学生由特殊归纳出一般情况“(长+宽)×2=长×2+宽×2”,并提问:“等式的左边乘了一个2,右边乘了两个2,左右两边还相等吗?‘(长+宽)×2=长+宽×2错在哪里?”很多学生都知道“(长+宽)×2=长+宽×2”不正确,但又说不出理由,这时我就用画图的方式引导学生找出问题所在。
在由直观模型向符号模型转化的过程中,教师可借助抽象程度不同的“形”引导学生一步步经历符号化的过程,最终提取运算律的符号模型。“(长+宽)×2=长×2+宽×2”这一乘法分配律的直观模型是建立在计算长方形周長的基础上的,能够培养学生构建数学模型解决问题的意识。因此,教师可进一步提问:“将长方形的长和宽分别变成a和b时,周长怎样算?a和b可以是多少?” “如果把2改成3,两个式子还相等吗?”……让学生模仿之前的模式,通过作图证明自己的想法。
接着,借助长方形的周长与组成长方形的四条线段之间的关系推理出“(a+b)×3=a×3+b×3”。
最后,通过不断添加线段,由形的延伸带动数的扩张:(a+b)×4=a×4+b×4,(a+b)×5=a×5+b×5,…,(a+b)×c=a×c+b×c,即乘法分配律。
在数形结合的过程中,学生通过乘法分配律的直观模型对乘法分配率的本质有了更深刻的理解,以后就不会犯类似“(5+3)×2=5+3×2”的错误了。可见,数形结合不但能帮助学生建构新知,理解运算定律的本质,还能提高学生简便计算的技能。
从生活出发,采用数形结合的方式让学生在脑海里构建运算定律的基本模型,那么学生对于乘法分配律的认知会更加深刻,由此构建的知识结构也更加完整,对学生的计算能力、数形结合意识、符号意识也会起到“润物细无声”的渗透作用。
(责编 童 夏)endprint

